简单的线性规划(二)
图片预览






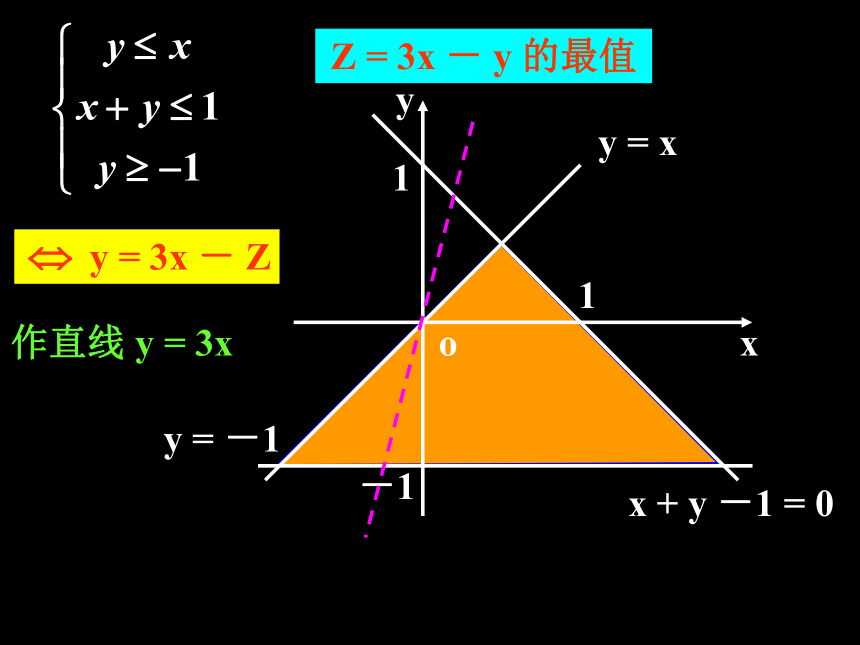
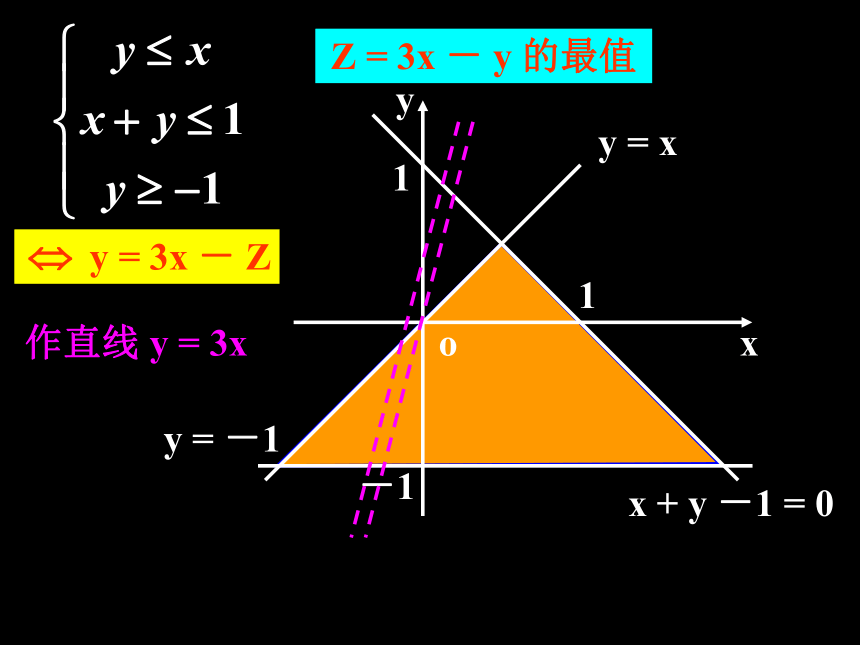
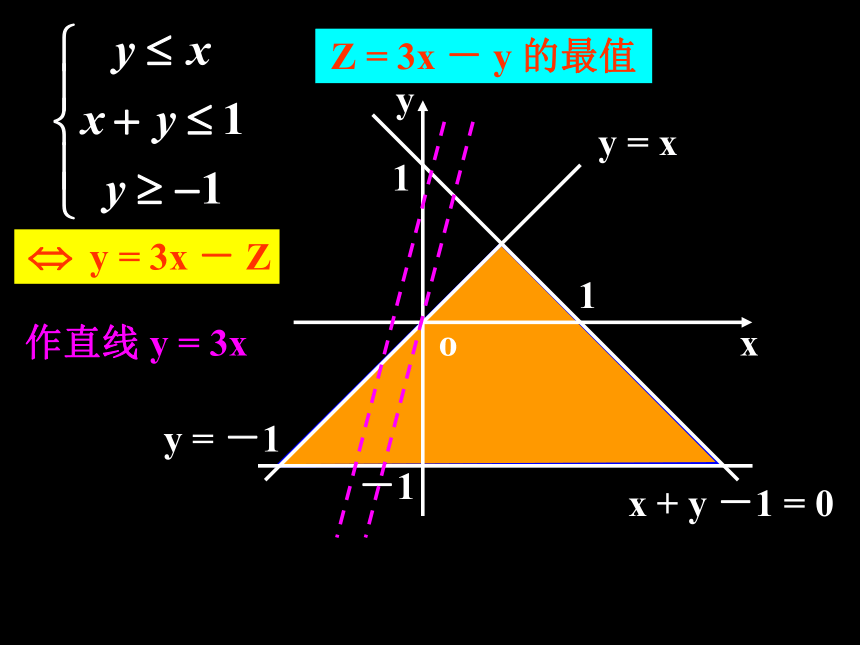

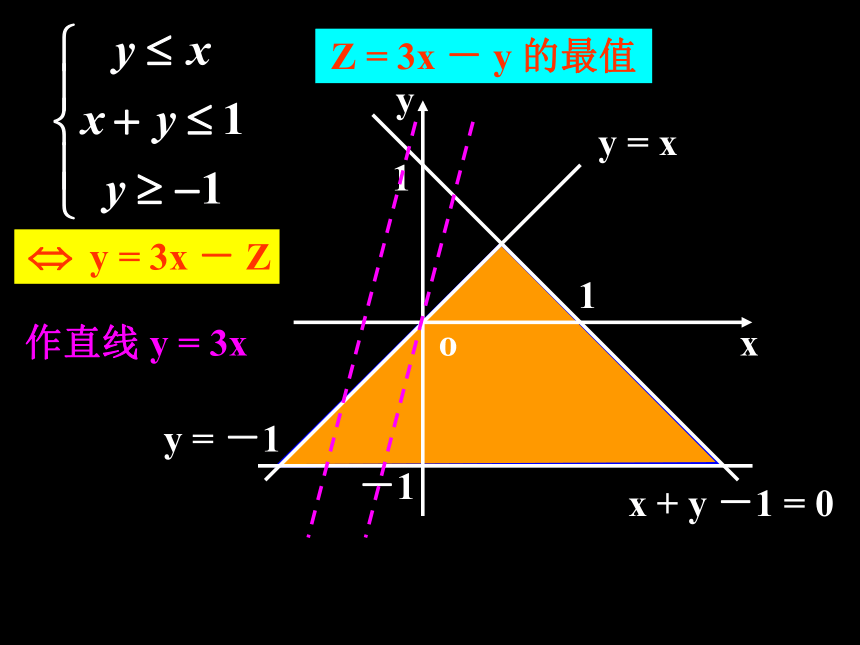
文档简介
课件71张PPT。简单的线性规划若实数x,y满足{按下列步骤进行: ①画:画满足不等式的点在坐标系中的区域; ②移:将Z=2x+y中的Z看作直线的纵截距,当直线 平移时观 平移时观察Z的取值情况,当直线与不等式 的 的区域有公共点时可得Z的取值范围 ③求:根据观察的结论,先求出区域内特殊点的坐标再求出Z的最大值和最小值 ④答:回答题目结论二、新授 ①、上述问题中x,y 的限制条件称为x,y 的约束条件。 由于x,y 都是一次的,又称约束条件为线性约束条件。 ② 、欲达到最值所涉及的变量x,y 的解析式称为目标函数。 关于x,y 的一次目标函数称为线性目标函数。 ③ 、求线性目标函数在线性约束条件下的最大值或最小值问题称 为线性规划问题。 ④、满足线性约束条件的解(x,y)称为可行解。⑤ 、使目标函数取得最大值或最小值的可行解称为最优解。所有可行解组成的集合称为可行域。1、[概念]2、?总结?解线性规划问题的步骤: (2)移:在线性目标函数所表示的一组平行
线中,利用平移的方法找出与可行域有公共
点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解及最值 (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;若实数x,y满足{… …①… …②求z=2x+y的最值[问题反思]{由{??解下列线性规划问题:1、求 Z = 3x -y 的最大值和最小值,使式中
的 x、y 满足约束条件
三、课堂练习Z = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ max = 7, Z min = -2Z = 3x - y 的最值作直线 y = 3x2、某公司承担了每天至少搬运280t水泥的任务,已知该公司有6辆A型卡车和4辆B型卡车,已知A型卡车每天每辆的运载量为30t,成本费为0.9千元,B型卡车每天每辆的运载量为40t,成本费为1千元。
(1)假设你是公司的调度员,请你按要求设计出公司每天的排车方案。
(2)设每天派出A型卡车x辆,B型卡车y辆,公司每天花费成本为Z千元,写出x、y应满足的条件以及Z与x、y之间的函数关系式。Z= 0.9x + y3x+4y≥28
0≤x≤6
0≤y≤4 课堂例题 1、某公司承担了每天至少搬运 280t 水泥的任务,已知该公司有 6 辆A型卡车和 4 辆B型卡车,已知A型卡车每天每辆的运载量为 30t,成本费为 0.9千元,B型卡车每天每辆的运载量为 40t,成本费为 1千元。
⑴假设你是公司的调度员,请你按要求设计出公司每天的排车方案。设每天派出A型卡车x辆,B型卡车y辆,
⑵若公司每天花费成本为Z千元,写出x、y应满足的条件以及Z与x、y之间的函数关系式。⑶如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各为多少辆Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z min = 7. 6此时应派A、B
卡车各4 辆Z = 0.9x + y 为最小解下列线性规划问题:三、课堂练习k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点由图知:最大值
的点为 ( 0 , 5 )k = 6x + 8y
取最大值时的点2、某木器厂生产圆桌和衣柜两种木料,第一种有 72 米 3,第二种有 56 米 3,假设生产每种产品都需要用两种木料,生产一张圆桌和一个衣柜分别所需要木料如表所示,每生产一张圆桌可获利润6元,生产一个衣柜可获利润10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得的利润最多?练习求 Z = 6x + 10y 的最大值( 350 , 100 )Z max = 3100 元几个结论:1、线性目标函数的最大(小)值一般在可
行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义
—— 在 y 轴上的截距或其相反数。
线中,利用平移的方法找出与可行域有公共
点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解及最值 (4)答:作出答案。 (1)画:画出线性约束条件所表示的可行域;若实数x,y满足{… …①… …②求z=2x+y的最值[问题反思]{由{??解下列线性规划问题:1、求 Z = 3x -y 的最大值和最小值,使式中
的 x、y 满足约束条件
三、课堂练习Z = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ = 3x - y 的最值作直线 y = 3xZ max = 7, Z min = -2Z = 3x - y 的最值作直线 y = 3x2、某公司承担了每天至少搬运280t水泥的任务,已知该公司有6辆A型卡车和4辆B型卡车,已知A型卡车每天每辆的运载量为30t,成本费为0.9千元,B型卡车每天每辆的运载量为40t,成本费为1千元。
(1)假设你是公司的调度员,请你按要求设计出公司每天的排车方案。
(2)设每天派出A型卡车x辆,B型卡车y辆,公司每天花费成本为Z千元,写出x、y应满足的条件以及Z与x、y之间的函数关系式。Z= 0.9x + y3x+4y≥28
0≤x≤6
0≤y≤4 课堂例题 1、某公司承担了每天至少搬运 280t 水泥的任务,已知该公司有 6 辆A型卡车和 4 辆B型卡车,已知A型卡车每天每辆的运载量为 30t,成本费为 0.9千元,B型卡车每天每辆的运载量为 40t,成本费为 1千元。
⑴假设你是公司的调度员,请你按要求设计出公司每天的排车方案。设每天派出A型卡车x辆,B型卡车y辆,
⑵若公司每天花费成本为Z千元,写出x、y应满足的条件以及Z与x、y之间的函数关系式。⑶如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各为多少辆Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z = 0.9x + y 为最小Z min = 7. 6此时应派A、B
卡车各4 辆Z = 0.9x + y 为最小解下列线性规划问题:三、课堂练习k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点k = 6x + 8y
取最大值时的点由图知:最大值
的点为 ( 0 , 5 )k = 6x + 8y
取最大值时的点2、某木器厂生产圆桌和衣柜两种木料,第一种有 72 米 3,第二种有 56 米 3,假设生产每种产品都需要用两种木料,生产一张圆桌和一个衣柜分别所需要木料如表所示,每生产一张圆桌可获利润6元,生产一个衣柜可获利润10元,木器厂在现有木料条件下,圆桌和衣柜各生产多少,才使获得的利润最多?练习求 Z = 6x + 10y 的最大值( 350 , 100 )Z max = 3100 元几个结论:1、线性目标函数的最大(小)值一般在可
行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析
线性目标函数所表示的几何意义
—— 在 y 轴上的截距或其相反数。
