江苏省南京九中2013届高三上学期文科数学第9周周练
文档属性
| 名称 | 江苏省南京九中2013届高三上学期文科数学第9周周练 | 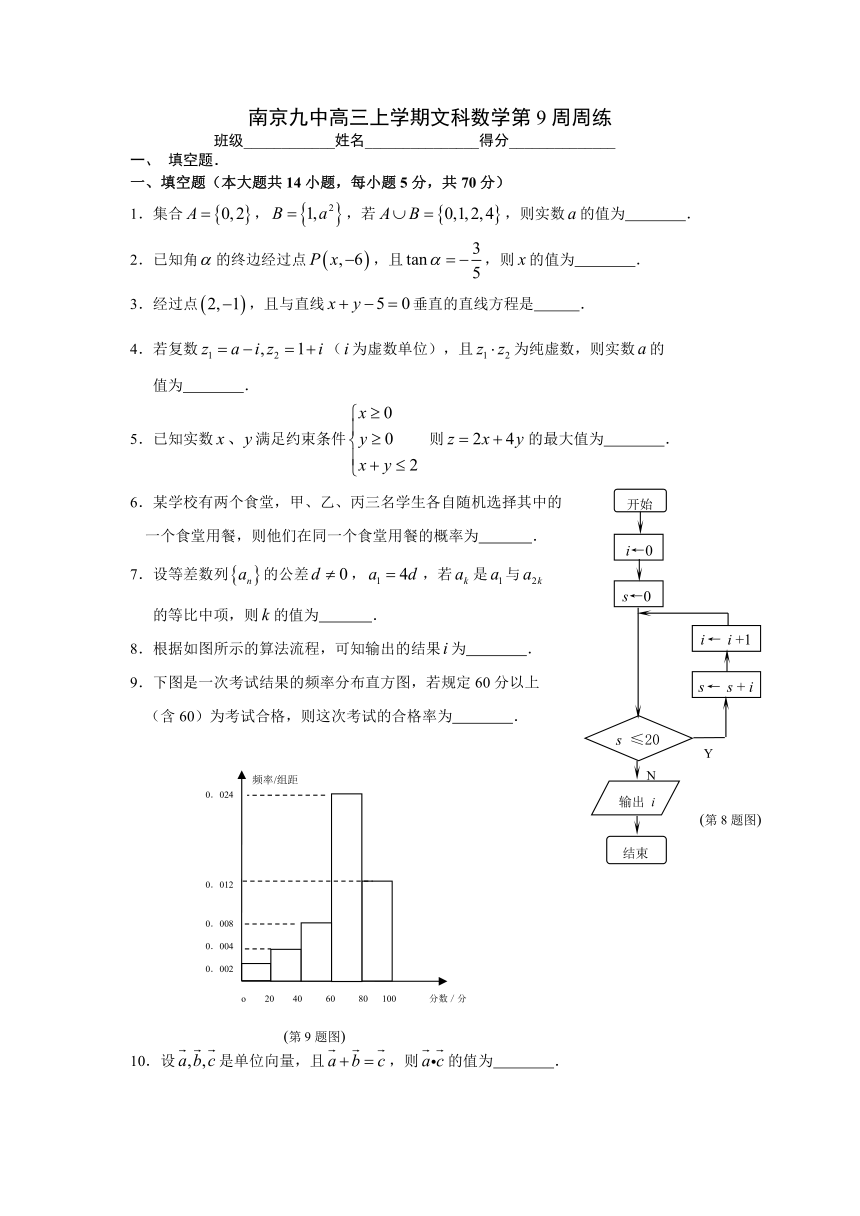 | |
| 格式 | zip | ||
| 文件大小 | 239.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-06 08:19:00 | ||
图片预览



文档简介
南京九中高三上学期文科数学第9周周练
班级____________姓名_______________得分______________
一、 填空题.
一、填空题(本大题共14小题,每小题5分,共70分)
1.集合,,若,则实数的值为 .
2.已知角的终边经过点,且,则的值为 .
3.经过点,且与直线垂直的直线方程是 .
4.若复数(为虚数单位),且为纯虚数,则实数的
值为 .
5.已知实数满足约束条件 则的最大值为 .
6.某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的
一个食堂用餐,则他们在同一个食堂用餐的概率为 .
7.设等差数列的公差,,若是与
的等比中项,则的值为 .
8.根据如图所示的算法流程,可知输出的结果为 .
9.下图是一次考试结果的频率分布直方图,若规定60分以上
(含60)为考试合格,则这次考试的合格率为 .
10.设是单位向量,且,则的值为 .
11.如图,已知正三棱柱的底面边长为2,高位5,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为 .
12.若不等式对恒成立,
则实数的取值范围是 .
13.五位同学围成一圈依次循环报数,规定,第一位同学首次
报出的数为2,第二位同学首次报出的数为3,之后每位
同学所报出的数都是前两位同学所报出数的乘积的个位数字,
则第2010个被报出的数为 .
14.设是由满足下列性质的函数构成的集合:
在定义域内存在,使得成立.已知下列函数:
①;②;③;④,其中属于集
合的函数是 (写出所有满足要求的函数的序号).
二、解答题(本大题共6小题,共90分。前三题18分每题,后两题21分每题。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分,第1小题5分,第2小题9分)
已知,,.
⑴若∥,求的值;
⑵若,求的值.
16.如图,在四棱锥中,四边形为平行四边形,,,
为上一点,且平面.
⑴求证:;
⑵如果点为线段的中点,求证:∥平面.
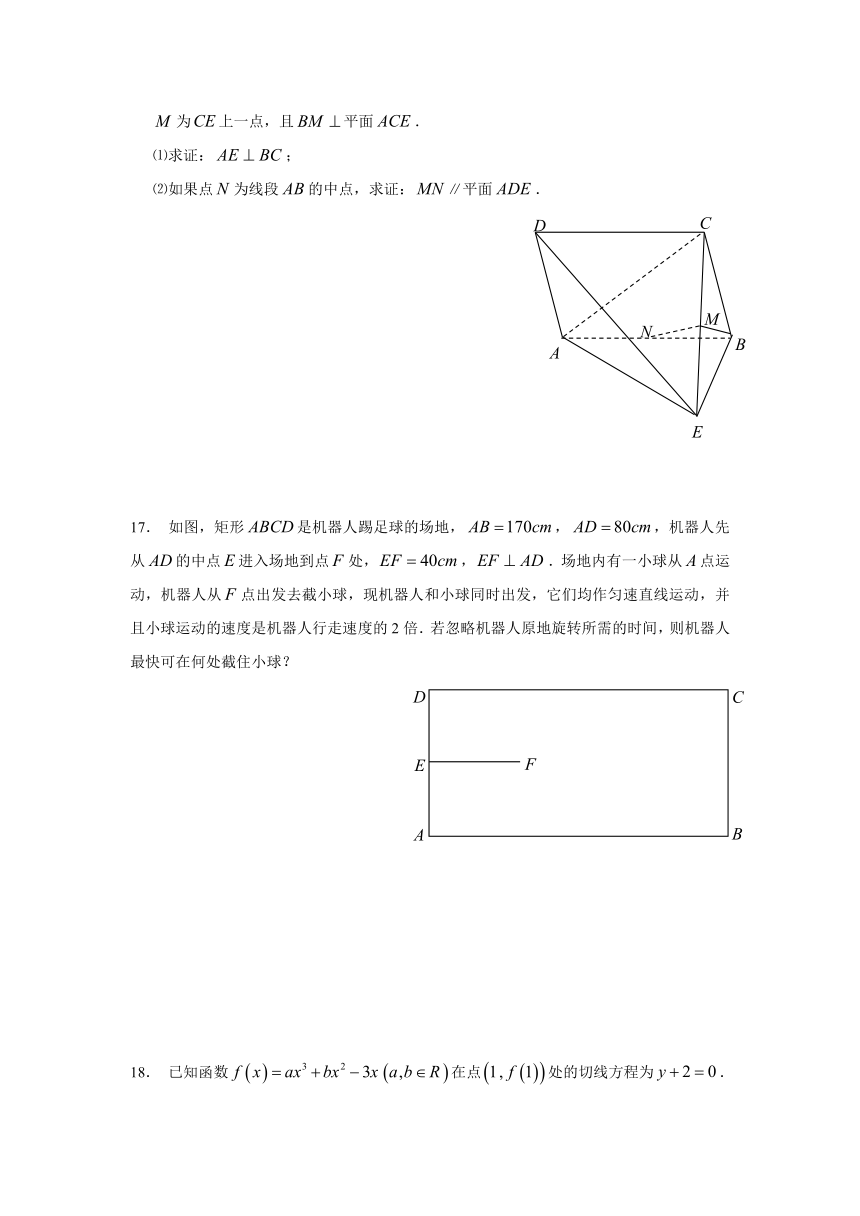
17. 如图,矩形是机器人踢足球的场地,,,机器人先从的中点进入场地到点处,,.场地内有一小球从点运动,机器人从点出发去截小球,现机器人和小球同时出发,它们均作匀速直线运动,并且小球运动的速度是机器人行走速度的2倍.若忽略机器人原地旋转所需的时间,则机器人最快可在何处截住小球?
18. 已知函数在点处的切线方程为.
⑴求函数的解析式;
⑵若对于区间上任意两个自变量的值都有,求实数的最小值;
⑶若过点可作曲线的三条切线,求实数的取值范围.
19.设函数,数列满足.
⑴求数列的通项公式;
⑵设,若对恒成立,求实数的取值范围;
⑶是否存在以为首项,公比为的数列,,使得数列中每一项都是数列中不同的项,若存在,求出所有满足条件的数列的通项公式;若不存在,说明理由.
南京九中第9周 周练答案
一、填空题(本大题共14小题,每小题5分,共70分)
1. 2.10 3. 4. 5.8 6. 7.3
8.7 9.72% 10. 11.13 12. 13.4 14.②④
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分,第1小题5分,第2小题9分)
解:⑴因为∥,所以.………………… ………………………3分
则.…………………………………………………………………………5分
⑵因为,所以,……………………………………7分
即.…………………………………………………………………………9分
因为,所以,则.…………………………11分
…………………………………………………14分
16.(本题满分14分,第1小题6分,第2小题8分)
证明:⑴因为平面,平面,所以.……………2分
因为,且,平面,
所以平面.……………………………………………………………………4分
因为平面,所以.………………………………………………6分
⑵取中点,连结.
因为平面,平面,所以.
因为,所以为的中点.………………………………………………8分
所以为△的中位线.所以∥,且=.……………10分
因为四边形为平行四边形,所以∥,且.
故∥,且.
因为为中点,所以∥,且.
所以四边形为平行四边形,所以∥.………………………………12分
因为平面,平面,所以∥平面.………………14分
17.(本题满分14分)
解:设该机器人最快可在点处截住小球 ,点在线段上.
设.根据题意,得 .
则.………………………………………………1分
连接,在△中,,,
所以, .………………………………………………2分
于是.在△中,由余弦定理,
得.
所以.………………8分
解得.………………………………………………………………12分
所以,或(不合题意,舍去).………13分
答:该机器人最快可在线段上离点70处截住小球.…………………………14分
18.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)
解:⑴.…………………………………………………………2分
根据题意,得即解得……………………3分
所以.………………………………………………………………4分
⑵令,即.得.
1
2
+
+
增
极大值
减
极小值
增
2
因为,,
所以当时,,.………………………………6分
则对于区间上任意两个自变量的值,都有
,所以.
所以的最小值为4.……………………………………………………………………8分
⑶因为点不在曲线上,所以可设切点为.
则.
因为,所以切线的斜率为.………………………………9分
则=,………………………………………………………………11分
即.
因为过点可作曲线的三条切线,
所以方程有三个不同的实数解.
所以函数有三个不同的零点.
则.令,则或.
0
2
+
+
增
极大值
减
极小值
增
则 ,即,解得.…………………………………16分
19.(本题满分16分,第1小题 4分,第2小题6分,第3小题6分)
解:⑴因为,
所以.…………………………………………………………………………2分
因为,所以数列是以1为首项,公差为的等差数列.
所以.…………………………………………………………………………4分
⑵①当时,
.…………………………………………………………………………6分
②当时,
.…………………………………………8分
所以
要使对恒成立,
只要使.
只要使,
故实数的取值范围为.……………………………………………………10分
⑶由,知数列中每一项都不可能是偶数.
①如存在以为首项,公比为2或4的数列,,
此时中每一项除第一项外都是偶数,故不存在以为首项,公比为偶数的数列.……………………………………………………………………………………12分
②当时,显然不存在这样的数列.
当时,若存在以为首项,公比为3的数列,.
则,,,.
所以满足条件的数列的通项公式为.……………………………………16分
班级____________姓名_______________得分______________
一、 填空题.
一、填空题(本大题共14小题,每小题5分,共70分)
1.集合,,若,则实数的值为 .
2.已知角的终边经过点,且,则的值为 .
3.经过点,且与直线垂直的直线方程是 .
4.若复数(为虚数单位),且为纯虚数,则实数的
值为 .
5.已知实数满足约束条件 则的最大值为 .
6.某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的
一个食堂用餐,则他们在同一个食堂用餐的概率为 .
7.设等差数列的公差,,若是与
的等比中项,则的值为 .
8.根据如图所示的算法流程,可知输出的结果为 .
9.下图是一次考试结果的频率分布直方图,若规定60分以上
(含60)为考试合格,则这次考试的合格率为 .
10.设是单位向量,且,则的值为 .
11.如图,已知正三棱柱的底面边长为2,高位5,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为 .
12.若不等式对恒成立,
则实数的取值范围是 .
13.五位同学围成一圈依次循环报数,规定,第一位同学首次
报出的数为2,第二位同学首次报出的数为3,之后每位
同学所报出的数都是前两位同学所报出数的乘积的个位数字,
则第2010个被报出的数为 .
14.设是由满足下列性质的函数构成的集合:
在定义域内存在,使得成立.已知下列函数:
①;②;③;④,其中属于集
合的函数是 (写出所有满足要求的函数的序号).
二、解答题(本大题共6小题,共90分。前三题18分每题,后两题21分每题。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分,第1小题5分,第2小题9分)
已知,,.
⑴若∥,求的值;
⑵若,求的值.
16.如图,在四棱锥中,四边形为平行四边形,,,
为上一点,且平面.
⑴求证:;
⑵如果点为线段的中点,求证:∥平面.
17. 如图,矩形是机器人踢足球的场地,,,机器人先从的中点进入场地到点处,,.场地内有一小球从点运动,机器人从点出发去截小球,现机器人和小球同时出发,它们均作匀速直线运动,并且小球运动的速度是机器人行走速度的2倍.若忽略机器人原地旋转所需的时间,则机器人最快可在何处截住小球?
18. 已知函数在点处的切线方程为.
⑴求函数的解析式;
⑵若对于区间上任意两个自变量的值都有,求实数的最小值;
⑶若过点可作曲线的三条切线,求实数的取值范围.
19.设函数,数列满足.
⑴求数列的通项公式;
⑵设,若对恒成立,求实数的取值范围;
⑶是否存在以为首项,公比为的数列,,使得数列中每一项都是数列中不同的项,若存在,求出所有满足条件的数列的通项公式;若不存在,说明理由.
南京九中第9周 周练答案
一、填空题(本大题共14小题,每小题5分,共70分)
1. 2.10 3. 4. 5.8 6. 7.3
8.7 9.72% 10. 11.13 12. 13.4 14.②④
二、解答题(本大题共6小题,共90分。解答应写出文字说明、证明过程或演算步骤)
15.(本题满分14分,第1小题5分,第2小题9分)
解:⑴因为∥,所以.………………… ………………………3分
则.…………………………………………………………………………5分
⑵因为,所以,……………………………………7分
即.…………………………………………………………………………9分
因为,所以,则.…………………………11分
…………………………………………………14分
16.(本题满分14分,第1小题6分,第2小题8分)
证明:⑴因为平面,平面,所以.……………2分
因为,且,平面,
所以平面.……………………………………………………………………4分
因为平面,所以.………………………………………………6分
⑵取中点,连结.
因为平面,平面,所以.
因为,所以为的中点.………………………………………………8分
所以为△的中位线.所以∥,且=.……………10分
因为四边形为平行四边形,所以∥,且.
故∥,且.
因为为中点,所以∥,且.
所以四边形为平行四边形,所以∥.………………………………12分
因为平面,平面,所以∥平面.………………14分
17.(本题满分14分)
解:设该机器人最快可在点处截住小球 ,点在线段上.
设.根据题意,得 .
则.………………………………………………1分
连接,在△中,,,
所以, .………………………………………………2分
于是.在△中,由余弦定理,
得.
所以.………………8分
解得.………………………………………………………………12分
所以,或(不合题意,舍去).………13分
答:该机器人最快可在线段上离点70处截住小球.…………………………14分
18.(本题满分16分,第1小题 4分,第2小题4分,第3小题8分)
解:⑴.…………………………………………………………2分
根据题意,得即解得……………………3分
所以.………………………………………………………………4分
⑵令,即.得.
1
2
+
+
增
极大值
减
极小值
增
2
因为,,
所以当时,,.………………………………6分
则对于区间上任意两个自变量的值,都有
,所以.
所以的最小值为4.……………………………………………………………………8分
⑶因为点不在曲线上,所以可设切点为.
则.
因为,所以切线的斜率为.………………………………9分
则=,………………………………………………………………11分
即.
因为过点可作曲线的三条切线,
所以方程有三个不同的实数解.
所以函数有三个不同的零点.
则.令,则或.
0
2
+
+
增
极大值
减
极小值
增
则 ,即,解得.…………………………………16分
19.(本题满分16分,第1小题 4分,第2小题6分,第3小题6分)
解:⑴因为,
所以.…………………………………………………………………………2分
因为,所以数列是以1为首项,公差为的等差数列.
所以.…………………………………………………………………………4分
⑵①当时,
.…………………………………………………………………………6分
②当时,
.…………………………………………8分
所以
要使对恒成立,
只要使.
只要使,
故实数的取值范围为.……………………………………………………10分
⑶由,知数列中每一项都不可能是偶数.
①如存在以为首项,公比为2或4的数列,,
此时中每一项除第一项外都是偶数,故不存在以为首项,公比为偶数的数列.……………………………………………………………………………………12分
②当时,显然不存在这样的数列.
当时,若存在以为首项,公比为3的数列,.
则,,,.
所以满足条件的数列的通项公式为.……………………………………16分
同课章节目录
