空间两点间的距离公式
图片预览







文档简介
课件21张PPT。§4.3.2
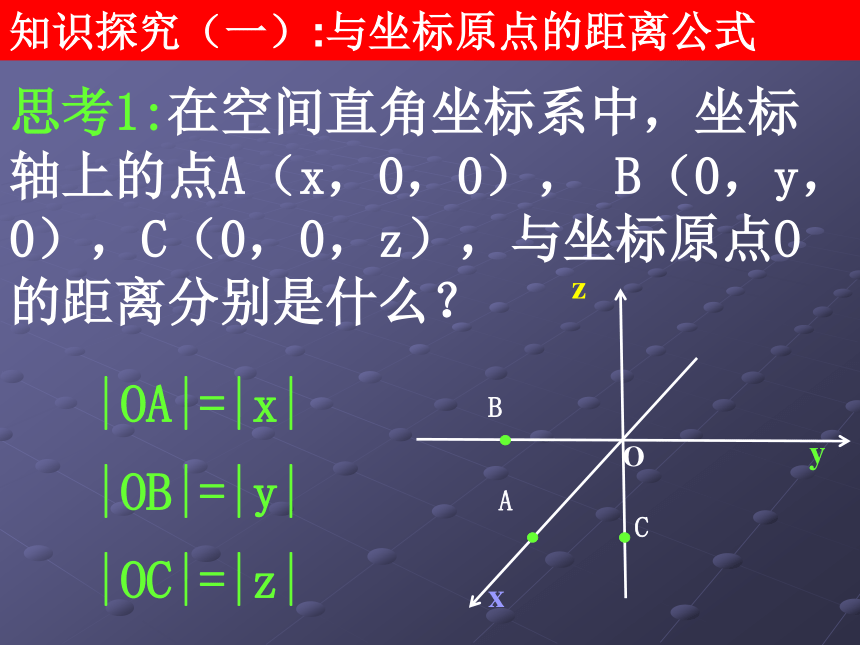
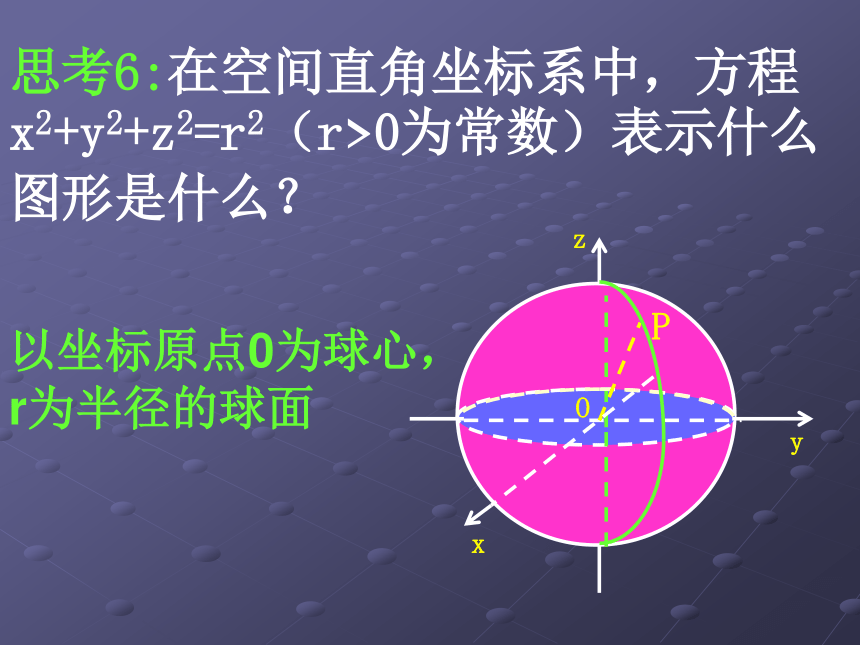
空间两点间的距离公式 问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.设A(x1,y1),B(x2,y2),空间两点间的距离公式知识探究(一):与坐标原点的距离公式 思考1:在空间直角坐标系中,坐标轴上的点A(x,0,0), B(0,y,0),C(0,0,z),与坐标原点O的距离分别是什么?|OA|=|x||OB|=|y||OC|=|z|思考2:在空间直角坐标系中,坐标平面上的点A(x,y,0),B(0,y,z),C(x,0,z),与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)在xOy平面上的射影为M,则点M的坐标是什么?|PM|,|OM|的值分别是什么?M(x,y,0)|PM|=|z|思考4:基于上述分析,你能得到点 P(x,y,z)与坐标原点O的距离公式吗?思考5:在平面直角坐标系中,方程 x2+y2=r2(r>0为常数)表示什么图形? 以坐标原点0为圆心,半径为r的圆P(x,y),0(0,0)换言之,|OP|是定长r思考6:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 以坐标原点0为球心,
r为半径的球面知识探究(二):空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),P2(x2,y2,z2)在xOy平面上的射影分别为M、N.思考1:点M、N之间的距离如何?M(x1,y1,0)
N(x2,y2,0)思考2:若直线P1P2垂直于xOy平面,则点P1、P2之间的距离如何?|P1P2|=|z1-z2|思考3:若直线P1P2平行于xOy平面,则点P1、P2之间的距离如何?思考4:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?例1 在空间中,已知点A(1, 0,-1),B (4, 3, -1),求A、B两点之间的距离.理论迁移例2 已知A(x,2,3)、B(5,4,7),且|AB|=6,求x的值.
解:|AB|=6,∴?
解得x=1或x=9.例3 在空间中,已知点 A(1,0,2),
B(1, -3,1),点P在z轴上,
若|PA|=|PB|,求点P的坐标.解:设P(0,0,Z)解得Z=-3
P(0,0,-3)例4 如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系0xyz。点P在正方体的对角线AB上,点Q在正方体的棱CD上(1)当点P为对角线AB的
中点,点Q在棱CD上运动时,
探究|PQ|的最小值,
并指出此时Q点的位置. (2)当点Q为棱CD上的中点,点P在对角线AB上运动时,探究|PQ|的最小值,并指出此时P点的位置.BACPQD(3)当点P在对角线AB上运动,点Q在棱CD上运动时,探究|PQ|的最小值,并指出此时P、Q两点的位置. H在棱长为a的正方体ABCD- A1B1C1D1中,求异面直线BD1与CC1间的距离问题转换要求异面直线BD1与CC1间的距离,即求P,Q两点间的最短距离。DP138 练习1、3、4
空间两点间的距离公式 问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.设A(x1,y1),B(x2,y2),空间两点间的距离公式知识探究(一):与坐标原点的距离公式 思考1:在空间直角坐标系中,坐标轴上的点A(x,0,0), B(0,y,0),C(0,0,z),与坐标原点O的距离分别是什么?|OA|=|x||OB|=|y||OC|=|z|思考2:在空间直角坐标系中,坐标平面上的点A(x,y,0),B(0,y,z),C(x,0,z),与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)在xOy平面上的射影为M,则点M的坐标是什么?|PM|,|OM|的值分别是什么?M(x,y,0)|PM|=|z|思考4:基于上述分析,你能得到点 P(x,y,z)与坐标原点O的距离公式吗?思考5:在平面直角坐标系中,方程 x2+y2=r2(r>0为常数)表示什么图形? 以坐标原点0为圆心,半径为r的圆P(x,y),0(0,0)换言之,|OP|是定长r思考6:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 以坐标原点0为球心,
r为半径的球面知识探究(二):空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),P2(x2,y2,z2)在xOy平面上的射影分别为M、N.思考1:点M、N之间的距离如何?M(x1,y1,0)
N(x2,y2,0)思考2:若直线P1P2垂直于xOy平面,则点P1、P2之间的距离如何?|P1P2|=|z1-z2|思考3:若直线P1P2平行于xOy平面,则点P1、P2之间的距离如何?思考4:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?例1 在空间中,已知点A(1, 0,-1),B (4, 3, -1),求A、B两点之间的距离.理论迁移例2 已知A(x,2,3)、B(5,4,7),且|AB|=6,求x的值.
解:|AB|=6,∴?
解得x=1或x=9.例3 在空间中,已知点 A(1,0,2),
B(1, -3,1),点P在z轴上,
若|PA|=|PB|,求点P的坐标.解:设P(0,0,Z)解得Z=-3
P(0,0,-3)例4 如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系0xyz。点P在正方体的对角线AB上,点Q在正方体的棱CD上(1)当点P为对角线AB的
中点,点Q在棱CD上运动时,
探究|PQ|的最小值,
并指出此时Q点的位置. (2)当点Q为棱CD上的中点,点P在对角线AB上运动时,探究|PQ|的最小值,并指出此时P点的位置.BACPQD(3)当点P在对角线AB上运动,点Q在棱CD上运动时,探究|PQ|的最小值,并指出此时P、Q两点的位置. H在棱长为a的正方体ABCD- A1B1C1D1中,求异面直线BD1与CC1间的距离问题转换要求异面直线BD1与CC1间的距离,即求P,Q两点间的最短距离。DP138 练习1、3、4
