2019-2020学年河北省邯郸市成安县七年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2019-2020学年河北省邯郸市成安县七年级(上)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 584.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 00:00:00 | ||
图片预览




文档简介
2019-2020学年河北省邯郸市成安县七年级第一学期期末数学试卷
一、准确选择(1-10每题3分,11-16每题2分,共42分)
1.若a与2互为相反数,则|a+2|等于( )
A.0 B.﹣2 C.2 D.4
2.下列说法中,正确的个数是( )
①若mx=my,则mx﹣my=0 ②若mx=my,则x=y
③若mx=my,则mx+my=2my④若x=y,则mx=my.
A.1 B.2 C.3 D.4
3.若|x﹣|+(2y+1)2=0,则x2+y2的值是( )
A. B. C.﹣ D.﹣
4.下面几何体从正面看得到的平面图形,哪一个和其他有明显的不同( )
A. B.
C. D.
5.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
6.如图,从点O出发,引四条射线OA、OB、OC、OD,则可以组成角的个数是( )
A.3个 B.4个 C.5个 D.6个
7.x=2是下列( )方程的解.
A.2(x﹣1)=6 B. C. D.
8.若关于x的方程3x+5=m与x﹣2m=5有相同的解,则m的值是( )
A.3 B.﹣3 C.﹣4 D.4
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连结A、B两点
C.画出直线AB的中点 D.画出A、B两点的距离
10.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
11.某超市进了一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
A.25%a元 B.(1﹣25%)a元 C.(1+25%)a元 D.元
12.下列各题正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7去括号、移项、合并同类项得x=5
13.如果代数式4y2﹣2y+5的值是7,那么代数式2y2﹣y+1的值等于( )
A.2 B.3 C.﹣2 D.4
14.某中学某班的学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见统计图,现给出以下说法:
①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的;
③最喜欢羽毛球的学生达到班级学生总数的.
其中正确的结论为( )
A.①② B.①③ C.②③ D.①②③
15.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清,被污染的方程是2y﹣5=y﹣●怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=3,很快补好了这个常数,这个常数应是( )
A.1 B.2 C.3 D.4
16.中国 湖南“崀山旅游节”开幕的当天,从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的人数约为600人,已知崀山景区游客的饱和人数约为2000人,那么开幕当天该景区的游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
二、仔细填空(每小题3分共12分)
17.今年母亲30岁,儿子2岁, 年后,母亲年龄是儿子年龄的5倍.
18.已知线段AB=4cm,B是线段AC的中点,则AC= cm.
19.如图是在一个半径为4厘米的圆内设计的图案,图案中阴影部分的面积是 平方厘米.
20.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如表所示.
点的个数 2 3 4 5 6 7
线段的条数 1 3 6 10 15 n
请你探究表内数据间的关系,根据发现的规律,则表中n= .
三、计算题(每题5分,共15分)
21.(1)4×(﹣3)2﹣13+(﹣)﹣|﹣43|.
(2)先化简,后求值:﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn],其中m=1,n=﹣2.
(3)解方程:x﹣=﹣3.
22.阅读下列材料:计算50÷(﹣+).
解法一:原式=50÷﹣50÷+50÷=50×3﹣50×4+50×12=550.
解法二:原式=50÷(﹣+)=50÷=50×6=300.
解法三:原式的倒数为(﹣+)÷50
=(﹣+)×=×﹣×+×=.
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的.请你选择合适的解法解答下列问题:
计算:(﹣)÷(﹣+﹣)
23.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA﹣∠BOC
=70°﹣15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
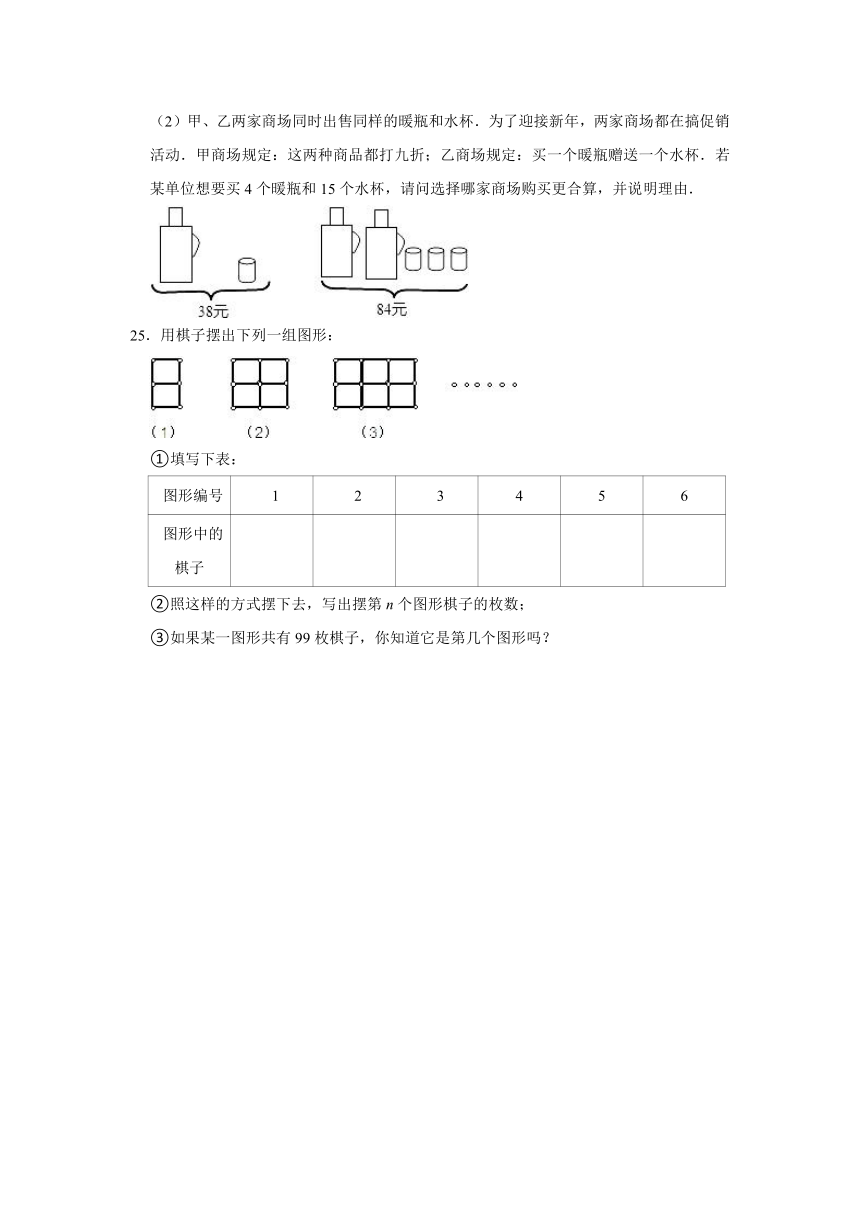
24.请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
25.用棋子摆出下列一组图形:
①填写下表:
图形编号 1 2 3 4 5 6
图形中的棋子
②照这样的方式摆下去,写出摆第n个图形棋子的枚数;
③如果某一图形共有99枚棋子,你知道它是第几个图形吗?
参考答案
一、准确选择(1-10每题3分,11-16每题2分,共42分)
1.若a与2互为相反数,则|a+2|等于( )
A.0 B.﹣2 C.2 D.4
【分析】根据绝对值的规律和相反数的定义求解即可.
解:因为互为相反数的两数和为0,所以a+2=0;0的绝对值是0,则|a+2|=|0|=0.
故选:A.
2.下列说法中,正确的个数是( )
①若mx=my,则mx﹣my=0 ②若mx=my,则x=y
③若mx=my,则mx+my=2my④若x=y,则mx=my.
A.1 B.2 C.3 D.4
【分析】利用等式的性质对每个式子进行变形即可找出答案.
解:①根据等式性质1,mx=my两边都减my,即可得到mx﹣my=0;
②根据等式性质2,需加条件m≠0;
③根据等式性质1,mx=my两边都加my,即可得到mx+my=2my;
④根据等式性质2,x=y两边都乘以m,即可得到mx=my;
综上所述,①③④正确;
故选:C.
3.若|x﹣|+(2y+1)2=0,则x2+y2的值是( )
A. B. C.﹣ D.﹣
【分析】先根据|x﹣|+(2y+1)2=0,可得出x﹣=0,2y+1=0,求出x、y的值,代入所求代数式进行计算即可.
解:∵|x﹣|+(2y+1)2=0,
∴x﹣=0,2y+1=0,
∴x=,y=﹣,
∴x2+y2=()2+(﹣)2=.
故选:B.
4.下面几何体从正面看得到的平面图形,哪一个和其他有明显的不同( )
A. B.
C. D.
【分析】找到从正面看所得到的图形比较即可.
解:A、C、D中的几何体从正面看得到的平面图形都是长方形,而B中几何体从正面看得到的平面图形是三角形,故选B.
5.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
【分析】根据线段之间的和差关系依次进行判断即可得出正确答案.
解:A、AD﹣CD=AB+BC,正确,
B、AC﹣BC=AD﹣BD,正确;
C、AC﹣BC=AB,而AC+BD≠AB,故本选项错误;
D、AD﹣AC=BD﹣BC,正确.
故选:C.
6.如图,从点O出发,引四条射线OA、OB、OC、OD,则可以组成角的个数是( )
A.3个 B.4个 C.5个 D.6个
【分析】分别以每一条射线为角的一边去数.
解:∠DOA,∠DOB,∠DOA,∠COB,∠COA,∠BOA,
所以可以组成6个角,
故选:D.
7.x=2是下列( )方程的解.
A.2(x﹣1)=6 B. C. D.
【分析】将x=2代入下列方程中进行一一验证即可.
解:A、当x=2时,左边=2,右边=6,左边≠右边;故本选项错误;
B、当x=2时,左边=,右边=1,左边≠右边;故本选项错误;
C、当x=2时,左边=2,右边=2,左边=右边;故本选项正确;
D、当x=2时,左边=,右边=﹣1,左边≠右边;故本选项错误.
故选:C.
8.若关于x的方程3x+5=m与x﹣2m=5有相同的解,则m的值是( )
A.3 B.﹣3 C.﹣4 D.4
【分析】分别用m的代数式表示出x,然后令两式相等,即可解出m的值.
解:3x+5=m,
∴m=3x+5①;
又x﹣2m=5,
∴m=②;
令①=②,
∴3x+5=,
6x+10﹣x+5=0,
∴x=﹣3,
故选:B.
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连结A、B两点
C.画出直线AB的中点 D.画出A、B两点的距离
【分析】根据直线,线段,射线的定义以及基本作图判断即可.
解:A、画射线OP=3cm,错误,射线没有长度,本选项不符合题意.
B、连结A、B两点,正确.本选项符合题意.
C、画出直线AB的中点,错误,直线没有长度,本选项不符合题意.
D、画出A、B两点的距离,错误,距离的一个数值,应该是量出A,B两点的距离.本选项不符合题意.
故选:B.
10.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
【分析】适合普查的方式一般有以下几种:
①范围较小;②容易掌控;③不具有破坏性;
④可操作性较强.
解:A、C、D中,容量太大,不易采用全面调查.B调查工作量小无破坏性,可以做全面调查.
故选:B.
11.某超市进了一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
A.25%a元 B.(1﹣25%)a元 C.(1+25%)a元 D.元
【分析】根据题意列等量关系式:售价=进价+利润.得解答时按等量关系直接求出售价.
解:依题意得,售价=进价+利润=进价×(1+利润率),
∴售价为(1+25%)a元.
故选:C.
12.下列各题正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7去括号、移项、合并同类项得x=5
【分析】根据解一元一次方程的步骤计算,并判断.
解:A、由7x=4x﹣3移项得7x﹣4x=﹣3,故错误;
B、由=1+去分母得2(2x﹣1)=6+3(x﹣3),故错误;
C、由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x+9=1,故错误;
D、正确.
故选:D.
13.如果代数式4y2﹣2y+5的值是7,那么代数式2y2﹣y+1的值等于( )
A.2 B.3 C.﹣2 D.4
【分析】根据4y2﹣2y+5的值是7得到2y2﹣y=1,然后利用整体代入思想计算即可.
解:∵4y2﹣2y+5=7,
∴2y2﹣y=1,
∴2y2﹣y+1=1+1=2.
故选:A.
14.某中学某班的学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见统计图,现给出以下说法:
①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的;
③最喜欢羽毛球的学生达到班级学生总数的.
其中正确的结论为( )
A.①② B.①③ C.②③ D.①②③
【分析】首先求得其它占总体的百分比为:1﹣48%﹣20%﹣20%=12%,然后对三句话进行判断.
解:由图可知,其它占总体的百分比为:1﹣48%﹣20%﹣20%=12%,所以最受欢迎的球类运动是乒乓球;
最喜欢排球的学生和喜欢羽毛球的学生都达到班级学生总数的;
错误的是③.
故选:A.
15.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清,被污染的方程是2y﹣5=y﹣●怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=3,很快补好了这个常数,这个常数应是( )
A.1 B.2 C.3 D.4
【分析】把y=3代入方程计算即可求出所求.
解:设常数为c,
把y=3代入方程得:6﹣5=3﹣c,
解得:c=2.
故选:B.
16.中国 湖南“崀山旅游节”开幕的当天,从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的人数约为600人,已知崀山景区游客的饱和人数约为2000人,那么开幕当天该景区的游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
【分析】设开幕当天该景区游客人数饱和的时间约为x点,结合已知条件“从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的游客人数约为600人,已知景区游客的饱和人数约为2000人”列出方程并解答.
解:设开幕式当天该景区游客人数饱和的时间约为x点,则
(x﹣8)×(1000﹣600)=2000,
解得:x=13.
即开幕式当天该景区游客人数饱和的时间约为13:00.
故选:C.
二、仔细填空(每小题3分共12分)
17.今年母亲30岁,儿子2岁, 5 年后,母亲年龄是儿子年龄的5倍.
【分析】设x年后,母亲年龄是儿子年龄的5倍,则x年后母亲的年龄是:30+x岁,儿子是:2+x岁.题目中的相等关系是:母亲年龄=5×儿子年龄,根据题意就可以列出方程求解.
解:根据题意得:30+x=5(2+x)
解得:x=5.
即5年后,母亲年龄是儿子年龄的5倍.
18.已知线段AB=4cm,B是线段AC的中点,则AC= 8 cm.
【分析】理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系.
解:∵AB=4cm,B是线段AC的中点,∴AC=2AB=2×4=8cm.
故答案为8.
19.如图是在一个半径为4厘米的圆内设计的图案,图案中阴影部分的面积是 8π 平方厘米.
【分析】直接利用图形的性质结合圆的面积求法得出答案.
解:由图形特点得出,阴影部分的面积是:=8π.
故答案为:8π.
20.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如表所示.
点的个数 2 3 4 5 6 7
线段的条数 1 3 6 10 15 n
请你探究表内数据间的关系,根据发现的规律,则表中n= 21 .
【分析】根据表中数据,寻找规律,列出公式解答.
解:设线段有n个点,分成的线段有m条.有以下规律:
n m
2 1
3 1+2
4 1+2+3
…
n m=1+…+(n﹣1)
=,
7个点把线段AB共分成=21条.
故答案为:21.
三、计算题(每题5分,共15分)
21.(1)4×(﹣3)2﹣13+(﹣)﹣|﹣43|.
(2)先化简,后求值:﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn],其中m=1,n=﹣2.
(3)解方程:x﹣=﹣3.
【分析】(1)先算乘方,再算乘除法和绝对值,最后算加法即可;
(2)先去括号,再合并同类项,然后将m=1,n=﹣2代入化简后的式子即可解答本题;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解:(1)原式=4×9﹣13﹣﹣64
=36﹣13﹣﹣64
=﹣41﹣
=﹣41;
(2)原式=﹣2mn+6m2﹣(m2﹣5mn+5m2+2mn)
=﹣2mn+6m2﹣(6m2﹣3mn)
=﹣2mn+6m2﹣6m2+3mn
=mn,
当m=1,n=﹣2时,原式=﹣2;
(3)解:去分母,得15x﹣3 (x﹣2)=5(2x﹣5)﹣45,
去括号,得15x﹣3x+6=10x﹣25﹣45,
移项,得15x﹣3x﹣10x=﹣6﹣25﹣45,
合并同类项,得2x=﹣76,
系数化成1,得x=﹣38.
22.阅读下列材料:计算50÷(﹣+).
解法一:原式=50÷﹣50÷+50÷=50×3﹣50×4+50×12=550.
解法二:原式=50÷(﹣+)=50÷=50×6=300.
解法三:原式的倒数为(﹣+)÷50
=(﹣+)×=×﹣×+×=.
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法 一 是错误的.请你选择合适的解法解答下列问题:
计算:(﹣)÷(﹣+﹣)
【分析】根据有理数的除法,可转化成有理数的乘法,可得答案;
根据有理数的运算顺序,先算括号里面的,再算有理数的除法,可得答案.
解:没有除法分配律,故解法一错误;
故答案为:一.
原式=()÷(﹣)
=(﹣)×3
=.
23.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA﹣∠BOC
=70°﹣15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
【分析】在同一平面内,若∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
解:如图,当OC在∠AOB的内部时,∠AOC=∠BOA﹣∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
24.请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
【分析】(1)等量关系为:2×暖瓶单价+3×(38﹣暖瓶单价)=84;
(2)甲商场付费:暖瓶和水杯总价之和×90%;乙商场付费:4×暖瓶单价+(15﹣4)×水杯单价.
解:(1)设一个暖瓶x元,则一个水杯(38﹣x)元,
根据题意得:2x+3(38﹣x)=84.
解得:x=30.
一个水杯=38﹣30=8(元).
故一个暖瓶30元,一个水杯8元;
(2)若到甲商场购买,则所需的钱数为:(4×30+15×8)×90%=216元.
若到乙商场购买,则所需的钱数为:4×30+(15﹣4)×8=208元.
因为208<216.
所以到乙家商场购买更合算.
25.用棋子摆出下列一组图形:
①填写下表:
图形编号 1 2 3 4 5 6
图形中的棋子
②照这样的方式摆下去,写出摆第n个图形棋子的枚数;
③如果某一图形共有99枚棋子,你知道它是第几个图形吗?
【分析】解题注意根据图形发现规律,并用字母表示.然后根据条件代入计算.
解:①
图形编号 1 2 3 4 5 6
图形中的棋子 6 9 12 15 18 21
②第n个图形棋子的枚数是6+3(n﹣1)=3n+3个.
③99=3n+3,n=32.
如果某一图形共有99枚棋子,它是第32个图形.
一、准确选择(1-10每题3分,11-16每题2分,共42分)
1.若a与2互为相反数,则|a+2|等于( )
A.0 B.﹣2 C.2 D.4
2.下列说法中,正确的个数是( )
①若mx=my,则mx﹣my=0 ②若mx=my,则x=y
③若mx=my,则mx+my=2my④若x=y,则mx=my.
A.1 B.2 C.3 D.4
3.若|x﹣|+(2y+1)2=0,则x2+y2的值是( )
A. B. C.﹣ D.﹣
4.下面几何体从正面看得到的平面图形,哪一个和其他有明显的不同( )
A. B.
C. D.
5.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
6.如图,从点O出发,引四条射线OA、OB、OC、OD,则可以组成角的个数是( )
A.3个 B.4个 C.5个 D.6个
7.x=2是下列( )方程的解.
A.2(x﹣1)=6 B. C. D.
8.若关于x的方程3x+5=m与x﹣2m=5有相同的解,则m的值是( )
A.3 B.﹣3 C.﹣4 D.4
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连结A、B两点
C.画出直线AB的中点 D.画出A、B两点的距离
10.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
11.某超市进了一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
A.25%a元 B.(1﹣25%)a元 C.(1+25%)a元 D.元
12.下列各题正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7去括号、移项、合并同类项得x=5
13.如果代数式4y2﹣2y+5的值是7,那么代数式2y2﹣y+1的值等于( )
A.2 B.3 C.﹣2 D.4
14.某中学某班的学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见统计图,现给出以下说法:
①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的;
③最喜欢羽毛球的学生达到班级学生总数的.
其中正确的结论为( )
A.①② B.①③ C.②③ D.①②③
15.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清,被污染的方程是2y﹣5=y﹣●怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=3,很快补好了这个常数,这个常数应是( )
A.1 B.2 C.3 D.4
16.中国 湖南“崀山旅游节”开幕的当天,从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的人数约为600人,已知崀山景区游客的饱和人数约为2000人,那么开幕当天该景区的游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
二、仔细填空(每小题3分共12分)
17.今年母亲30岁,儿子2岁, 年后,母亲年龄是儿子年龄的5倍.
18.已知线段AB=4cm,B是线段AC的中点,则AC= cm.
19.如图是在一个半径为4厘米的圆内设计的图案,图案中阴影部分的面积是 平方厘米.
20.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如表所示.
点的个数 2 3 4 5 6 7
线段的条数 1 3 6 10 15 n
请你探究表内数据间的关系,根据发现的规律,则表中n= .
三、计算题(每题5分,共15分)
21.(1)4×(﹣3)2﹣13+(﹣)﹣|﹣43|.
(2)先化简,后求值:﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn],其中m=1,n=﹣2.
(3)解方程:x﹣=﹣3.
22.阅读下列材料:计算50÷(﹣+).
解法一:原式=50÷﹣50÷+50÷=50×3﹣50×4+50×12=550.
解法二:原式=50÷(﹣+)=50÷=50×6=300.
解法三:原式的倒数为(﹣+)÷50
=(﹣+)×=×﹣×+×=.
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法 是错误的.请你选择合适的解法解答下列问题:
计算:(﹣)÷(﹣+﹣)
23.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA﹣∠BOC
=70°﹣15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
24.请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
25.用棋子摆出下列一组图形:
①填写下表:
图形编号 1 2 3 4 5 6
图形中的棋子
②照这样的方式摆下去,写出摆第n个图形棋子的枚数;
③如果某一图形共有99枚棋子,你知道它是第几个图形吗?
参考答案
一、准确选择(1-10每题3分,11-16每题2分,共42分)
1.若a与2互为相反数,则|a+2|等于( )
A.0 B.﹣2 C.2 D.4
【分析】根据绝对值的规律和相反数的定义求解即可.
解:因为互为相反数的两数和为0,所以a+2=0;0的绝对值是0,则|a+2|=|0|=0.
故选:A.
2.下列说法中,正确的个数是( )
①若mx=my,则mx﹣my=0 ②若mx=my,则x=y
③若mx=my,则mx+my=2my④若x=y,则mx=my.
A.1 B.2 C.3 D.4
【分析】利用等式的性质对每个式子进行变形即可找出答案.
解:①根据等式性质1,mx=my两边都减my,即可得到mx﹣my=0;
②根据等式性质2,需加条件m≠0;
③根据等式性质1,mx=my两边都加my,即可得到mx+my=2my;
④根据等式性质2,x=y两边都乘以m,即可得到mx=my;
综上所述,①③④正确;
故选:C.
3.若|x﹣|+(2y+1)2=0,则x2+y2的值是( )
A. B. C.﹣ D.﹣
【分析】先根据|x﹣|+(2y+1)2=0,可得出x﹣=0,2y+1=0,求出x、y的值,代入所求代数式进行计算即可.
解:∵|x﹣|+(2y+1)2=0,
∴x﹣=0,2y+1=0,
∴x=,y=﹣,
∴x2+y2=()2+(﹣)2=.
故选:B.
4.下面几何体从正面看得到的平面图形,哪一个和其他有明显的不同( )
A. B.
C. D.
【分析】找到从正面看所得到的图形比较即可.
解:A、C、D中的几何体从正面看得到的平面图形都是长方形,而B中几何体从正面看得到的平面图形是三角形,故选B.
5.如图,下列关系式中与图不符合的式子是( )
A.AD﹣CD=AB+BC B.AC﹣BC=AD﹣BD
C.AC﹣BC=AC+BD D.AD﹣AC=BD﹣BC
【分析】根据线段之间的和差关系依次进行判断即可得出正确答案.
解:A、AD﹣CD=AB+BC,正确,
B、AC﹣BC=AD﹣BD,正确;
C、AC﹣BC=AB,而AC+BD≠AB,故本选项错误;
D、AD﹣AC=BD﹣BC,正确.
故选:C.
6.如图,从点O出发,引四条射线OA、OB、OC、OD,则可以组成角的个数是( )
A.3个 B.4个 C.5个 D.6个
【分析】分别以每一条射线为角的一边去数.
解:∠DOA,∠DOB,∠DOA,∠COB,∠COA,∠BOA,
所以可以组成6个角,
故选:D.
7.x=2是下列( )方程的解.
A.2(x﹣1)=6 B. C. D.
【分析】将x=2代入下列方程中进行一一验证即可.
解:A、当x=2时,左边=2,右边=6,左边≠右边;故本选项错误;
B、当x=2时,左边=,右边=1,左边≠右边;故本选项错误;
C、当x=2时,左边=2,右边=2,左边=右边;故本选项正确;
D、当x=2时,左边=,右边=﹣1,左边≠右边;故本选项错误.
故选:C.
8.若关于x的方程3x+5=m与x﹣2m=5有相同的解,则m的值是( )
A.3 B.﹣3 C.﹣4 D.4
【分析】分别用m的代数式表示出x,然后令两式相等,即可解出m的值.
解:3x+5=m,
∴m=3x+5①;
又x﹣2m=5,
∴m=②;
令①=②,
∴3x+5=,
6x+10﹣x+5=0,
∴x=﹣3,
故选:B.
9.下列画图语句中,正确的是( )
A.画射线OP=3cm B.连结A、B两点
C.画出直线AB的中点 D.画出A、B两点的距离
【分析】根据直线,线段,射线的定义以及基本作图判断即可.
解:A、画射线OP=3cm,错误,射线没有长度,本选项不符合题意.
B、连结A、B两点,正确.本选项符合题意.
C、画出直线AB的中点,错误,直线没有长度,本选项不符合题意.
D、画出A、B两点的距离,错误,距离的一个数值,应该是量出A,B两点的距离.本选项不符合题意.
故选:B.
10.下面调查中,适合做全面调查的是( )
A.某品牌的大米在市场上的占有率
B.今天班上有几名同学打扫教室
C.某款汽车每百公里的耗油量
D.春节晚会的收视率
【分析】适合普查的方式一般有以下几种:
①范围较小;②容易掌控;③不具有破坏性;
④可操作性较强.
解:A、C、D中,容量太大,不易采用全面调查.B调查工作量小无破坏性,可以做全面调查.
故选:B.
11.某超市进了一批商品,每件进价为a元,若要获利25%,则每件商品的零售价应定为( )
A.25%a元 B.(1﹣25%)a元 C.(1+25%)a元 D.元
【分析】根据题意列等量关系式:售价=进价+利润.得解答时按等量关系直接求出售价.
解:依题意得,售价=进价+利润=进价×(1+利润率),
∴售价为(1+25%)a元.
故选:C.
12.下列各题正确的是( )
A.由7x=4x﹣3移项得7x﹣4x=3
B.由=1+去分母得2(2x﹣1)=1+3(x﹣3)
C.由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1
D.由2(x+1)=x+7去括号、移项、合并同类项得x=5
【分析】根据解一元一次方程的步骤计算,并判断.
解:A、由7x=4x﹣3移项得7x﹣4x=﹣3,故错误;
B、由=1+去分母得2(2x﹣1)=6+3(x﹣3),故错误;
C、由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x+9=1,故错误;
D、正确.
故选:D.
13.如果代数式4y2﹣2y+5的值是7,那么代数式2y2﹣y+1的值等于( )
A.2 B.3 C.﹣2 D.4
【分析】根据4y2﹣2y+5的值是7得到2y2﹣y=1,然后利用整体代入思想计算即可.
解:∵4y2﹣2y+5=7,
∴2y2﹣y=1,
∴2y2﹣y+1=1+1=2.
故选:A.
14.某中学某班的学生喜欢各类体育活动,他们最喜欢的一项体育活动情况见统计图,现给出以下说法:
①最受欢迎的球类运动是乒乓球;
②最喜欢排球的学生达到班级学生总数的;
③最喜欢羽毛球的学生达到班级学生总数的.
其中正确的结论为( )
A.①② B.①③ C.②③ D.①②③
【分析】首先求得其它占总体的百分比为:1﹣48%﹣20%﹣20%=12%,然后对三句话进行判断.
解:由图可知,其它占总体的百分比为:1﹣48%﹣20%﹣20%=12%,所以最受欢迎的球类运动是乒乓球;
最喜欢排球的学生和喜欢羽毛球的学生都达到班级学生总数的;
错误的是③.
故选:A.
15.小明在做解方程作业时,不小心将方程中的一个常数污染了看不清,被污染的方程是2y﹣5=y﹣●怎么办呢?小明想了一想便翻看了书后的答案,此方程的解是y=3,很快补好了这个常数,这个常数应是( )
A.1 B.2 C.3 D.4
【分析】把y=3代入方程计算即可求出所求.
解:设常数为c,
把y=3代入方程得:6﹣5=3﹣c,
解得:c=2.
故选:B.
16.中国 湖南“崀山旅游节”开幕的当天,从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的人数约为600人,已知崀山景区游客的饱和人数约为2000人,那么开幕当天该景区的游客人数饱和的时间约为( )
A.10:00 B.12:00 C.13:00 D.16:00
【分析】设开幕当天该景区游客人数饱和的时间约为x点,结合已知条件“从早晨8:00开始每小时进入景区的游客人数约为1000人,同时每小时走出景区的游客人数约为600人,已知景区游客的饱和人数约为2000人”列出方程并解答.
解:设开幕式当天该景区游客人数饱和的时间约为x点,则
(x﹣8)×(1000﹣600)=2000,
解得:x=13.
即开幕式当天该景区游客人数饱和的时间约为13:00.
故选:C.
二、仔细填空(每小题3分共12分)
17.今年母亲30岁,儿子2岁, 5 年后,母亲年龄是儿子年龄的5倍.
【分析】设x年后,母亲年龄是儿子年龄的5倍,则x年后母亲的年龄是:30+x岁,儿子是:2+x岁.题目中的相等关系是:母亲年龄=5×儿子年龄,根据题意就可以列出方程求解.
解:根据题意得:30+x=5(2+x)
解得:x=5.
即5年后,母亲年龄是儿子年龄的5倍.
18.已知线段AB=4cm,B是线段AC的中点,则AC= 8 cm.
【分析】理解线段的中点这一概念,灵活运用线段的和、差、倍、分转化线段之间的数量关系.
解:∵AB=4cm,B是线段AC的中点,∴AC=2AB=2×4=8cm.
故答案为8.
19.如图是在一个半径为4厘米的圆内设计的图案,图案中阴影部分的面积是 8π 平方厘米.
【分析】直接利用图形的性质结合圆的面积求法得出答案.
解:由图形特点得出,阴影部分的面积是:=8π.
故答案为:8π.
20.一条直线上有若干个点,以任意两点为端点可以确定一条线段,线段的条数与点的个数之间的对应关系如表所示.
点的个数 2 3 4 5 6 7
线段的条数 1 3 6 10 15 n
请你探究表内数据间的关系,根据发现的规律,则表中n= 21 .
【分析】根据表中数据,寻找规律,列出公式解答.
解:设线段有n个点,分成的线段有m条.有以下规律:
n m
2 1
3 1+2
4 1+2+3
…
n m=1+…+(n﹣1)
=,
7个点把线段AB共分成=21条.
故答案为:21.
三、计算题(每题5分,共15分)
21.(1)4×(﹣3)2﹣13+(﹣)﹣|﹣43|.
(2)先化简,后求值:﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn],其中m=1,n=﹣2.
(3)解方程:x﹣=﹣3.
【分析】(1)先算乘方,再算乘除法和绝对值,最后算加法即可;
(2)先去括号,再合并同类项,然后将m=1,n=﹣2代入化简后的式子即可解答本题;
(3)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解:(1)原式=4×9﹣13﹣﹣64
=36﹣13﹣﹣64
=﹣41﹣
=﹣41;
(2)原式=﹣2mn+6m2﹣(m2﹣5mn+5m2+2mn)
=﹣2mn+6m2﹣(6m2﹣3mn)
=﹣2mn+6m2﹣6m2+3mn
=mn,
当m=1,n=﹣2时,原式=﹣2;
(3)解:去分母,得15x﹣3 (x﹣2)=5(2x﹣5)﹣45,
去括号,得15x﹣3x+6=10x﹣25﹣45,
移项,得15x﹣3x﹣10x=﹣6﹣25﹣45,
合并同类项,得2x=﹣76,
系数化成1,得x=﹣38.
22.阅读下列材料:计算50÷(﹣+).
解法一:原式=50÷﹣50÷+50÷=50×3﹣50×4+50×12=550.
解法二:原式=50÷(﹣+)=50÷=50×6=300.
解法三:原式的倒数为(﹣+)÷50
=(﹣+)×=×﹣×+×=.
故原式=300.
上述得出的结果不同,肯定有错误的解法,你认为解法 一 是错误的.请你选择合适的解法解答下列问题:
计算:(﹣)÷(﹣+﹣)
【分析】根据有理数的除法,可转化成有理数的乘法,可得答案;
根据有理数的运算顺序,先算括号里面的,再算有理数的除法,可得答案.
解:没有除法分配律,故解法一错误;
故答案为:一.
原式=()÷(﹣)
=(﹣)×3
=.
23.下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°,求∠AOC的度数.
解:根据题意可画出图
∵∠AOC=∠BOA﹣∠BOC
=70°﹣15°
=55°
∴∠AOC=55°
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的错误指出,并给出你认为正确的解法.
【分析】在同一平面内,若∠BOA与∠BOC可能存在两种情况,即当OC在∠AOB的内部或OC在∠AOB的外部.
解:如图,当OC在∠AOB的内部时,∠AOC=∠BOA﹣∠BOC=55°,
当OC在∠AOB的外部时,∠AOC=∠BOA+∠BOC=85°,
故∠AOC的度数是55°或85°.
24.请根据图中提供的信息,回答下列问题:
(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯.为了迎接新年,两家商场都在搞促销活动.甲商场规定:这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯.若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
【分析】(1)等量关系为:2×暖瓶单价+3×(38﹣暖瓶单价)=84;
(2)甲商场付费:暖瓶和水杯总价之和×90%;乙商场付费:4×暖瓶单价+(15﹣4)×水杯单价.
解:(1)设一个暖瓶x元,则一个水杯(38﹣x)元,
根据题意得:2x+3(38﹣x)=84.
解得:x=30.
一个水杯=38﹣30=8(元).
故一个暖瓶30元,一个水杯8元;
(2)若到甲商场购买,则所需的钱数为:(4×30+15×8)×90%=216元.
若到乙商场购买,则所需的钱数为:4×30+(15﹣4)×8=208元.
因为208<216.
所以到乙家商场购买更合算.
25.用棋子摆出下列一组图形:
①填写下表:
图形编号 1 2 3 4 5 6
图形中的棋子
②照这样的方式摆下去,写出摆第n个图形棋子的枚数;
③如果某一图形共有99枚棋子,你知道它是第几个图形吗?
【分析】解题注意根据图形发现规律,并用字母表示.然后根据条件代入计算.
解:①
图形编号 1 2 3 4 5 6
图形中的棋子 6 9 12 15 18 21
②第n个图形棋子的枚数是6+3(n﹣1)=3n+3个.
③99=3n+3,n=32.
如果某一图形共有99枚棋子,它是第32个图形.
同课章节目录
