人B版(2019)数学-必修第二册-第六章向量-§1.2向量的加法PPT(25张ppt)
文档属性
| 名称 | 人B版(2019)数学-必修第二册-第六章向量-§1.2向量的加法PPT(25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 10:00:36 | ||
图片预览







文档简介
(共25张PPT)
6.1.2向量的加法
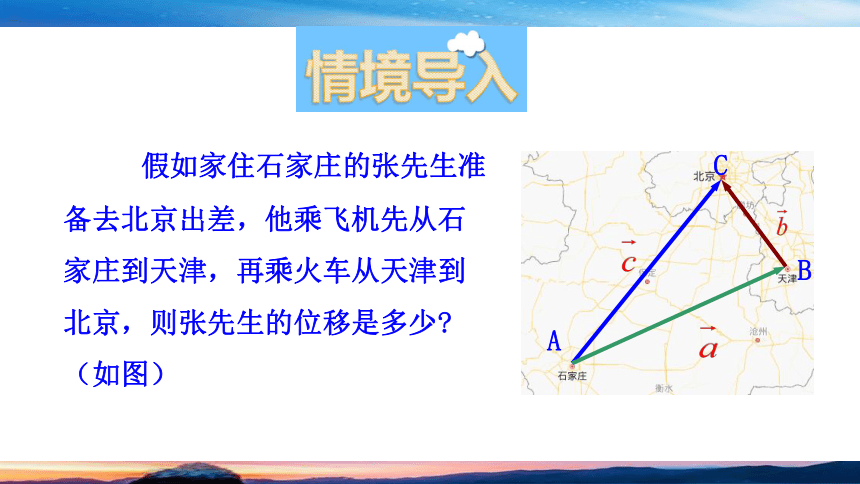
假如家住石家庄的张先生准备去北京出差,他乘飞机先从石家庄到天津,再乘火车从天津到北京,则张先生的位移是多少
(如图)
A
B
C
A
B
C
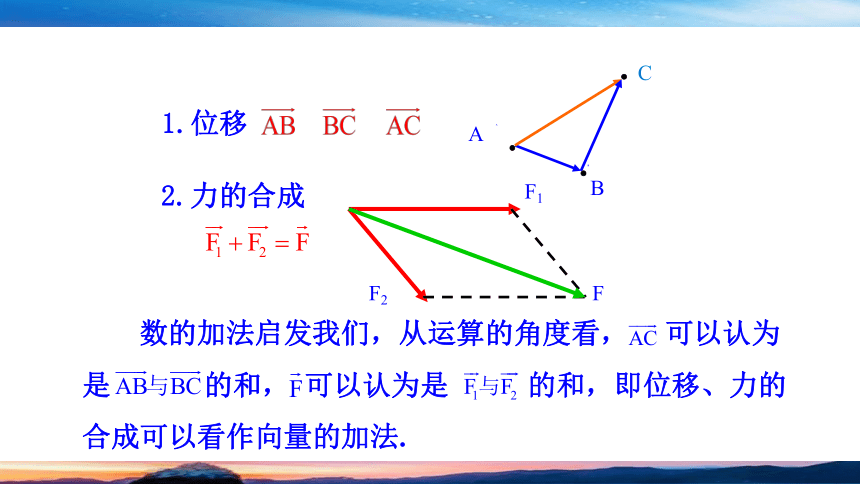
1.位移
2.力的合成
数的加法启发我们,从运算的角度看, 可以认为是 的和, 可以认为是 的和,即位移、力的合成可以看作向量的加法.
A
B
C
F1
F2
F
1.掌握向量加法的运算,并理解其几何意义.2.理解向量加法的三角形法则、平行四边形法则、多边形法则的适用范围,并能应用向量加法的运算律进行相关运算.
1.通过向量加法的三角形法则和平行四边形法则的学习,培养直观想象核心素养.2.通过学习向量加法的运算律,培养逻辑推理素养.
课标要求
素养要求
探究点1 向量加法的三角形法则
如图所示,假设某人上午从点A到达了点B,
下午从点B到达了点C.
(1)分别用向量表示出该人上午的位移,
下午的位移及一天的位移;
(2)这一天的位移与上午下午的位移有什么联系?试从大小和方向两个方面加以阐述
(3)上面两个向量及和向量构成三角形,若不能构成三角形呢,两向量应该有什么关系,和向量应该怎样表示?
位移 可以看成位移 与 的和.
a+b
0
a
a
方向相反
方向相同
例1 已知|a|=3,|b|=4,求向量a+b模长的最大值和最小值,并说明取到最大值和最小值是a,b的关系.
探究点2 向量加法的平行四边形法则
情景与问题
问题1 从物理学中我们已经知道,力既有
大小又有方向,因此力是向量.
当在光滑的水平面上沿着两个不同的方向拉动一个静止的物体时,物体会沿着力AB或AD的方向运动吗?若不会,物体的运动方向是怎样的呢?
问题2 数的加法运算满足交换律,由例1判断向量的加法运算是否满足交换律?
探究点3 多个向量相加
问题1 由向量加法的两个法则我们知道两个向量的和还是向量,因此我们可以用得到的和向量与另外一个向量相加.而且我们也知道数的加法满足结合律,那么向量的加法是否也满足结合律?也就是说三个向量相加,最后的结果是否与求和顺序有关?
问题2 多个向量相加,最后的结果与求和顺序有关吗?怎样确定和向量呢?
给出了三个向量a,b,c;先作出了向量a+b,然后作出了向量(a+b)+c;先作出了向量b+c,然后作出了向量a+(b+c);容易看出:
(a+b)+c=a+(b+c)即满足结合律
向量加法的三角形法则可以推广为多个向量求和的多边形法则,
即把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向量就是这些向量的和向量.
1、向量加法的定义
2、向量加法的三角形法则、平行四边形法则、多边形法则
3、向量加法的运算律
4、向量加法模的三角形不等式
世间没有一种具有真正价值的东西,可以不经过艰苦辛勤的劳动而得到。
6.1.2向量的加法
假如家住石家庄的张先生准备去北京出差,他乘飞机先从石家庄到天津,再乘火车从天津到北京,则张先生的位移是多少
(如图)
A
B
C
A
B
C
1.位移
2.力的合成
数的加法启发我们,从运算的角度看, 可以认为是 的和, 可以认为是 的和,即位移、力的合成可以看作向量的加法.
A
B
C
F1
F2
F
1.掌握向量加法的运算,并理解其几何意义.2.理解向量加法的三角形法则、平行四边形法则、多边形法则的适用范围,并能应用向量加法的运算律进行相关运算.
1.通过向量加法的三角形法则和平行四边形法则的学习,培养直观想象核心素养.2.通过学习向量加法的运算律,培养逻辑推理素养.
课标要求
素养要求
探究点1 向量加法的三角形法则
如图所示,假设某人上午从点A到达了点B,
下午从点B到达了点C.
(1)分别用向量表示出该人上午的位移,
下午的位移及一天的位移;
(2)这一天的位移与上午下午的位移有什么联系?试从大小和方向两个方面加以阐述
(3)上面两个向量及和向量构成三角形,若不能构成三角形呢,两向量应该有什么关系,和向量应该怎样表示?
位移 可以看成位移 与 的和.
a+b
0
a
a
方向相反
方向相同
例1 已知|a|=3,|b|=4,求向量a+b模长的最大值和最小值,并说明取到最大值和最小值是a,b的关系.
探究点2 向量加法的平行四边形法则
情景与问题
问题1 从物理学中我们已经知道,力既有
大小又有方向,因此力是向量.
当在光滑的水平面上沿着两个不同的方向拉动一个静止的物体时,物体会沿着力AB或AD的方向运动吗?若不会,物体的运动方向是怎样的呢?
问题2 数的加法运算满足交换律,由例1判断向量的加法运算是否满足交换律?
探究点3 多个向量相加
问题1 由向量加法的两个法则我们知道两个向量的和还是向量,因此我们可以用得到的和向量与另外一个向量相加.而且我们也知道数的加法满足结合律,那么向量的加法是否也满足结合律?也就是说三个向量相加,最后的结果是否与求和顺序有关?
问题2 多个向量相加,最后的结果与求和顺序有关吗?怎样确定和向量呢?
给出了三个向量a,b,c;先作出了向量a+b,然后作出了向量(a+b)+c;先作出了向量b+c,然后作出了向量a+(b+c);容易看出:
(a+b)+c=a+(b+c)即满足结合律
向量加法的三角形法则可以推广为多个向量求和的多边形法则,
即把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最后一个向量终点的向量就是这些向量的和向量.
1、向量加法的定义
2、向量加法的三角形法则、平行四边形法则、多边形法则
3、向量加法的运算律
4、向量加法模的三角形不等式
世间没有一种具有真正价值的东西,可以不经过艰苦辛勤的劳动而得到。
