人B版(2019)数学-必修第二册-第六章向量-§2.3平面向量的坐标及其运算(共28张PPT)
文档属性
| 名称 | 人B版(2019)数学-必修第二册-第六章向量-§2.3平面向量的坐标及其运算(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 10:53:23 | ||
图片预览







文档简介
(共28张PPT)
6.2.3 平面向量的坐标及其运算
在物理的学习中我们知道:飞机沿仰角为α的方向起飞的速度v,可分解为水平方向的速度vcos α和竖直方向的速度vsin α.
把一个向量分解到两个不同的方向,特别是在两个互相垂直的方向分解,可使许多度量问题变得较为简单,这就是向量的正交分解.
有了向量的正交分解,向量就可用平面直角坐标表示,从此向量的计算就转化为坐标的代数运算.
本节我们就学习向量的正交分解
和向量的坐标表示.
1.掌握平面向量的正交分解及其坐标表示.2.会用坐标表示平面向量的加、减与数乘向量运算.3.会用坐标表示平面向量共线的条件,能用向量共线的条件来解决有关向量共线、直线平行及点共线等问题.
1.通过学习向量的正交分解,培养数学抽象的核心素养.
2.通过向量的直角坐标运算,提升数学运算的核心素养.
课标要求
素养要求
(1)向量的垂直:平面上的两个非零向量a,b,如果它们所在的直线互相垂直,则称向量a,b垂直,记作a⊥b.
规定:零向量与任意向量都垂直.
探究点1 平面向量的坐标
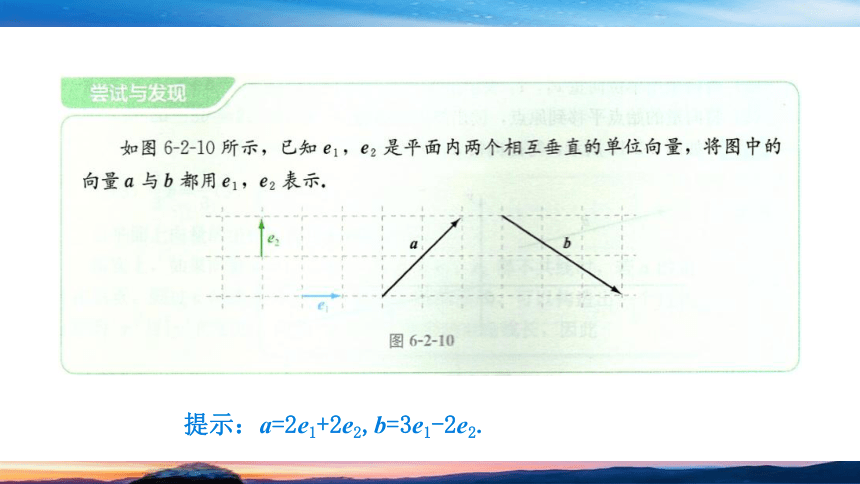
提示:a=2e1+2e2,b=3e1-2e2.
(2)向量的正交分解:如果平面向量的基底{e1,e2}中,e1⊥e2,则称这组基底为正交基底,在正交基底下向量的分解称为向量的正交分解.
(3)向量的坐标:给定平面内两个相互垂直的单位向量e1,e2,对于平面内的向量a,如果
a=xe1+ye2,
则称(x,y)为向量a的坐标,记作a=(x,y).
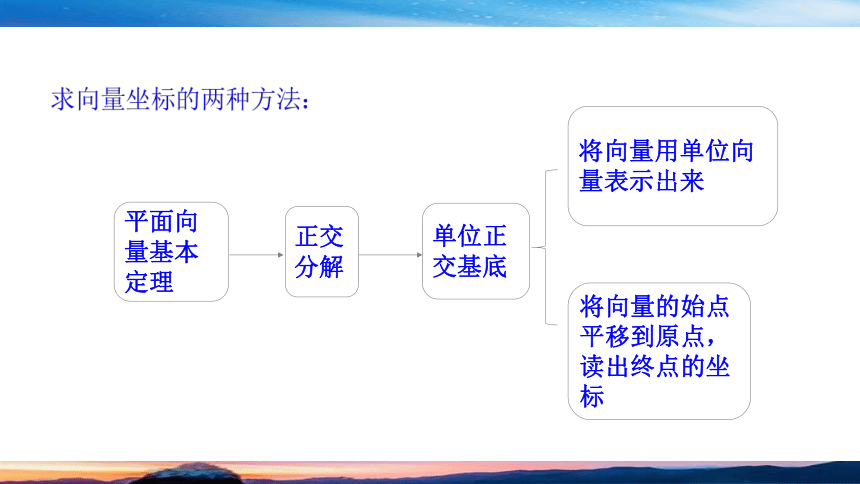
平面向量基本定理
正交分解
单位正交基底
将向量用单位向量表示出来
将向量的始点平移到原点,读出终点的坐标
探究点2 平面上向量的运算与坐标关系
探究点3 平面直角坐标系内两点之间的距离公式与中点坐标公式
探究点4 向量平行的坐标表示
B
B
A
-1
一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚.
——谢觉哉
6.2.3 平面向量的坐标及其运算
在物理的学习中我们知道:飞机沿仰角为α的方向起飞的速度v,可分解为水平方向的速度vcos α和竖直方向的速度vsin α.
把一个向量分解到两个不同的方向,特别是在两个互相垂直的方向分解,可使许多度量问题变得较为简单,这就是向量的正交分解.
有了向量的正交分解,向量就可用平面直角坐标表示,从此向量的计算就转化为坐标的代数运算.
本节我们就学习向量的正交分解
和向量的坐标表示.
1.掌握平面向量的正交分解及其坐标表示.2.会用坐标表示平面向量的加、减与数乘向量运算.3.会用坐标表示平面向量共线的条件,能用向量共线的条件来解决有关向量共线、直线平行及点共线等问题.
1.通过学习向量的正交分解,培养数学抽象的核心素养.
2.通过向量的直角坐标运算,提升数学运算的核心素养.
课标要求
素养要求
(1)向量的垂直:平面上的两个非零向量a,b,如果它们所在的直线互相垂直,则称向量a,b垂直,记作a⊥b.
规定:零向量与任意向量都垂直.
探究点1 平面向量的坐标
提示:a=2e1+2e2,b=3e1-2e2.
(2)向量的正交分解:如果平面向量的基底{e1,e2}中,e1⊥e2,则称这组基底为正交基底,在正交基底下向量的分解称为向量的正交分解.
(3)向量的坐标:给定平面内两个相互垂直的单位向量e1,e2,对于平面内的向量a,如果
a=xe1+ye2,
则称(x,y)为向量a的坐标,记作a=(x,y).
平面向量基本定理
正交分解
单位正交基底
将向量用单位向量表示出来
将向量的始点平移到原点,读出终点的坐标
探究点2 平面上向量的运算与坐标关系
探究点3 平面直角坐标系内两点之间的距离公式与中点坐标公式
探究点4 向量平行的坐标表示
B
B
A
-1
一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚.
——谢觉哉
