人B版(2019)数学-必修第二册-第六章向量-§3平面向量线性运算的应用(共21张PPT)
文档属性
| 名称 | 人B版(2019)数学-必修第二册-第六章向量-§3平面向量线性运算的应用(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
6.3平面向量线性运算的应用
英国科学家赫胥黎应邀到都柏林大学演讲,由于时间紧迫,他一跳上出租车,就急着说:“快!快!来不及了!”司机遵照指示,猛开了几分钟,赫胥黎才发现不太对劲,问道:“我没有说要去哪里吗 ”司机回答:“没有啊!你只叫我快开啊!”
赫胥黎于是说:“对不起,请掉头,我要
去都柏林.”我国古代也有南辕北辙的
故事.由此可见,速度不仅有大小,而且
还有方向.在我们生活中,有太多的事
物不仅与表示它的量的大小有关,而且也与方向有关.
1.会用向量法计算或证明平面几何中的相关问题
2.会用向量法解决某些简单的物理学中的问题.
1.通过向量在几何中应用的学习,培养数学运算及数学建模核心素养.
2.通过向量在物理中的应用,培养数学建模的核心素养.
课标要求
素养要求
1.向量在平面几何中的应用
在学习向量及其运算时,我们已经看到向量在三角形、平行四边形等平面几何中的应用.实际上,利用平面向量可以很好地描述有关全等、相似、平行等关系,从而可以求解和证明平面几何问题.
(1)证明线段平行问题,常用向量平行(共线)的等价条件:a∥b(b≠0)a=λbx1 y2-x2 y1=0.
(2)求线段的长度或证明线段相等,可利用向量的线性运算、向量模的公式|a|=.
探究点1 向量在平面几何中的应用
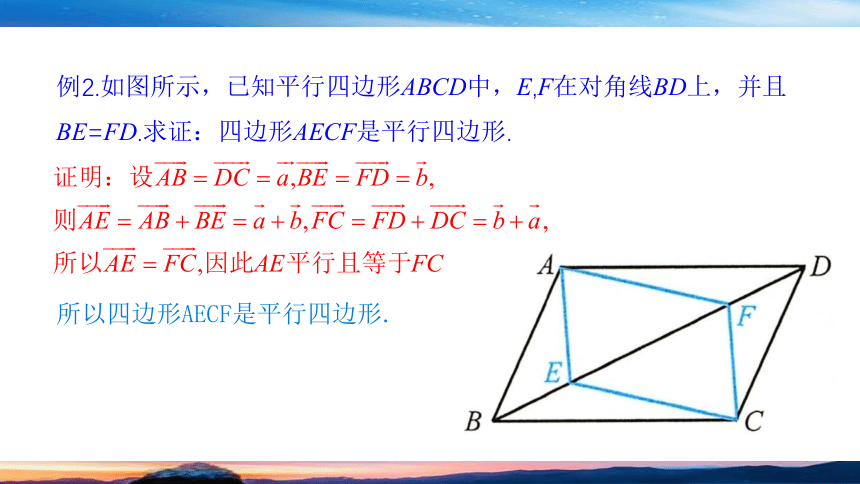
例2.如图所示,已知平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.求证:四边形AECF是平行四边形.
所以四边形AECF是平行四边形.
1.向量在物理中的应用
我们在物理中已经学习过,利用向量可以描述物理学中的位移、力、速度、加速度等,因此,在涉及这些量的运算时,我们都可以借助向量来完成.
探究点2 向量在物理中的应用
如果两个力F1,F2的合力为零,则F1+F2=0,
也就是说,这两个力互为相反向量.
如果三个力F1,F2,F3的合力为零,则F1+F2+F3=0,
也就是说,其中任意两个力的合力是另外一个力的相反向量.
D
C
D
A
1.用向量方法解决平面几何问题“三步曲”
①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
②通过向量运算,研究几何元素之间的关系,如距离、平行等;
③把运算结果“翻译”成几何问题的答案.
2.用向量求解平面几何问题的两种方法
①向量几何法:选取适当的基底(基底中的向量尽量已知模或夹角),将题中涉及的向量用基底表示,利用向量的运算法则、运算律或性质计算.
②向量坐标法:建立平面直角坐标系,实现向量的坐标化,将几何问题中的长度、平行等问题转化为代数问题.
3.利用向量法解决物理问题的步骤
(1)抽象出物理问题中的向量,转化为数学问题;
(2)建立以向量为主体的数学模型;
(3)利用向量的线性运算或坐标运算求解数学模型;
(4)用数学模型中的数据解释或分析物理问题.
一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚.
——谢觉哉
6.3平面向量线性运算的应用
英国科学家赫胥黎应邀到都柏林大学演讲,由于时间紧迫,他一跳上出租车,就急着说:“快!快!来不及了!”司机遵照指示,猛开了几分钟,赫胥黎才发现不太对劲,问道:“我没有说要去哪里吗 ”司机回答:“没有啊!你只叫我快开啊!”
赫胥黎于是说:“对不起,请掉头,我要
去都柏林.”我国古代也有南辕北辙的
故事.由此可见,速度不仅有大小,而且
还有方向.在我们生活中,有太多的事
物不仅与表示它的量的大小有关,而且也与方向有关.
1.会用向量法计算或证明平面几何中的相关问题
2.会用向量法解决某些简单的物理学中的问题.
1.通过向量在几何中应用的学习,培养数学运算及数学建模核心素养.
2.通过向量在物理中的应用,培养数学建模的核心素养.
课标要求
素养要求
1.向量在平面几何中的应用
在学习向量及其运算时,我们已经看到向量在三角形、平行四边形等平面几何中的应用.实际上,利用平面向量可以很好地描述有关全等、相似、平行等关系,从而可以求解和证明平面几何问题.
(1)证明线段平行问题,常用向量平行(共线)的等价条件:a∥b(b≠0)a=λbx1 y2-x2 y1=0.
(2)求线段的长度或证明线段相等,可利用向量的线性运算、向量模的公式|a|=.
探究点1 向量在平面几何中的应用
例2.如图所示,已知平行四边形ABCD中,E,F在对角线BD上,并且BE=FD.求证:四边形AECF是平行四边形.
所以四边形AECF是平行四边形.
1.向量在物理中的应用
我们在物理中已经学习过,利用向量可以描述物理学中的位移、力、速度、加速度等,因此,在涉及这些量的运算时,我们都可以借助向量来完成.
探究点2 向量在物理中的应用
如果两个力F1,F2的合力为零,则F1+F2=0,
也就是说,这两个力互为相反向量.
如果三个力F1,F2,F3的合力为零,则F1+F2+F3=0,
也就是说,其中任意两个力的合力是另外一个力的相反向量.
D
C
D
A
1.用向量方法解决平面几何问题“三步曲”
①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
②通过向量运算,研究几何元素之间的关系,如距离、平行等;
③把运算结果“翻译”成几何问题的答案.
2.用向量求解平面几何问题的两种方法
①向量几何法:选取适当的基底(基底中的向量尽量已知模或夹角),将题中涉及的向量用基底表示,利用向量的运算法则、运算律或性质计算.
②向量坐标法:建立平面直角坐标系,实现向量的坐标化,将几何问题中的长度、平行等问题转化为代数问题.
3.利用向量法解决物理问题的步骤
(1)抽象出物理问题中的向量,转化为数学问题;
(2)建立以向量为主体的数学模型;
(3)利用向量的线性运算或坐标运算求解数学模型;
(4)用数学模型中的数据解释或分析物理问题.
一知半解的人,多不谦虚;见多识广有本领的人,一定谦虚.
——谢觉哉
