3.1直线的倾斜角与斜率课件-2021-2022学年高一上学期数学人教A版必修2(共17张PPT)
文档属性
| 名称 | 3.1直线的倾斜角与斜率课件-2021-2022学年高一上学期数学人教A版必修2(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 711.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 11:01:21 | ||
图片预览




文档简介
(共17张PPT)
第三章 直线与方程
3.1 直线的倾斜角与斜率
3.1.1 倾斜角与斜率
坐标法是解析几何中最基本的研究方法,它是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.
P●
x
y
o
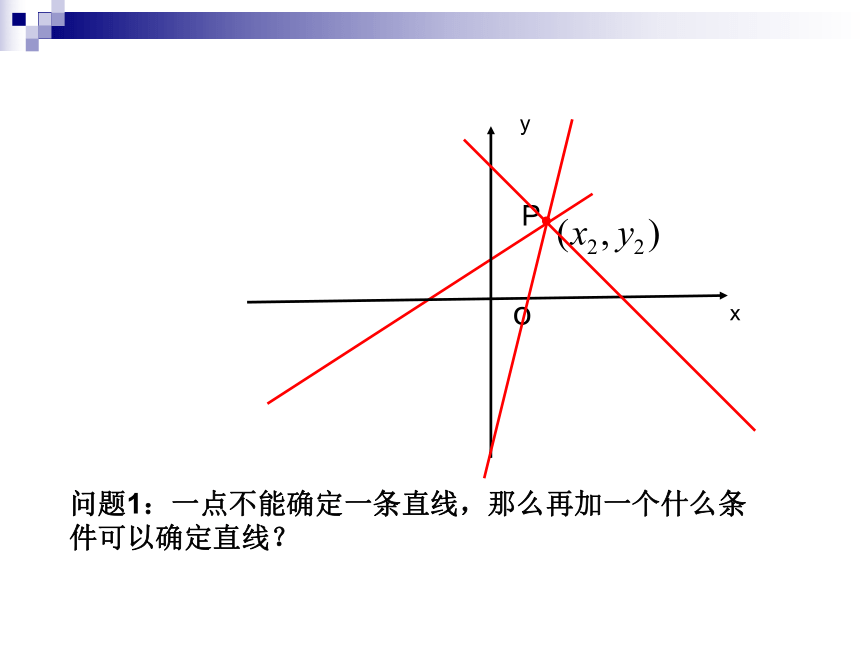
问题1:一点不能确定一条直线,那么再加一个什么条件可以确定直线?
问题2:下面哪一条上山的路陡一些?
P
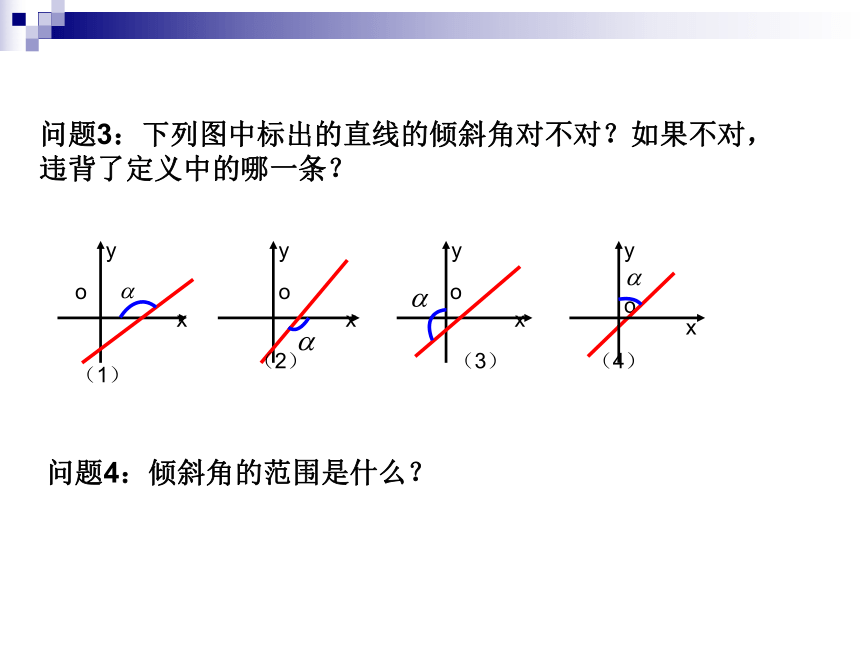
问题3:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
o
x
y
o
x
y
o
x
y
o
x
y
(1)
(2)
(3)
(4)
问题4:倾斜角的范围是什么?
前进量
升高量
升高量
前进量
A
B
C
设直线的倾斜程度为k
直线的斜率:
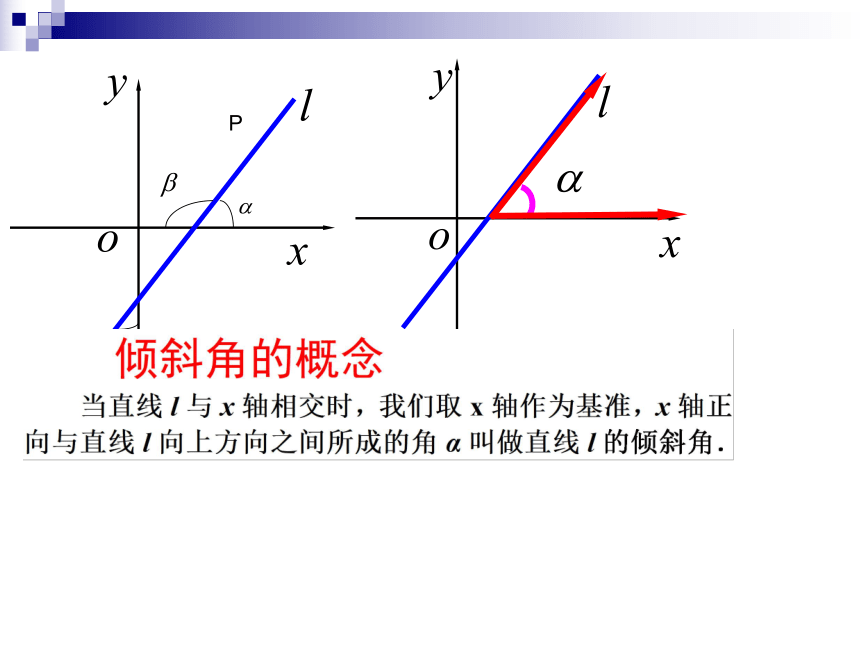
定义:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
用小写字母 k 表示,即:
问题6:下列叙述正确么?(1)平行于X轴的直线的倾斜角是0°或 180°.
(2)平行于Y轴的直线的斜率不存在,所以倾斜角也不存在。
(3)若直线的斜率存在,则倾斜角存在.
(4)每一条直线都唯一对应一个倾斜角.
(5)若直线倾斜角为α,则直线的斜率为tanα.
问题7:已知直线的倾斜角,直线的斜率是多少 :
(1)α=0° (2)α=30°; (3)α=45°; (4)α=60°; (5)α=90°; (6)α=120°; (7)α=135°; (8)α=150°;
问题8:填写下表
倾斜角 α=0° 0°<α<90° α=90° 90°<α<180°
斜率
斜率增减性
K=0
K不存在
K>0
K<0
k随α增大
而增大
k随α增大
而增大
问题9:已知直线经过点 ,能求出它的斜率么?
当 为钝角时,
在直角 中
同样,当 的方向向上时,也有
经过两点
的直线的斜率公式:
直线的斜率公式:
【课堂小结】
数形结合
斜率公式
斜率定义
倾斜角
应用
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休”. - -----华罗庚
第三章 直线与方程
3.1 直线的倾斜角与斜率
3.1.1 倾斜角与斜率
坐标法是解析几何中最基本的研究方法,它是以坐标系为桥梁,把几何问题转化成代数问题,通过代数运算研究几何图形性质的方法.
P●
x
y
o
问题1:一点不能确定一条直线,那么再加一个什么条件可以确定直线?
问题2:下面哪一条上山的路陡一些?
P
问题3:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
o
x
y
o
x
y
o
x
y
o
x
y
(1)
(2)
(3)
(4)
问题4:倾斜角的范围是什么?
前进量
升高量
升高量
前进量
A
B
C
设直线的倾斜程度为k
直线的斜率:
定义:
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率.
用小写字母 k 表示,即:
问题6:下列叙述正确么?(1)平行于X轴的直线的倾斜角是0°或 180°.
(2)平行于Y轴的直线的斜率不存在,所以倾斜角也不存在。
(3)若直线的斜率存在,则倾斜角存在.
(4)每一条直线都唯一对应一个倾斜角.
(5)若直线倾斜角为α,则直线的斜率为tanα.
问题7:已知直线的倾斜角,直线的斜率是多少 :
(1)α=0° (2)α=30°; (3)α=45°; (4)α=60°; (5)α=90°; (6)α=120°; (7)α=135°; (8)α=150°;
问题8:填写下表
倾斜角 α=0° 0°<α<90° α=90° 90°<α<180°
斜率
斜率增减性
K=0
K不存在
K>0
K<0
k随α增大
而增大
k随α增大
而增大
问题9:已知直线经过点 ,能求出它的斜率么?
当 为钝角时,
在直角 中
同样,当 的方向向上时,也有
经过两点
的直线的斜率公式:
直线的斜率公式:
【课堂小结】
数形结合
斜率公式
斜率定义
倾斜角
应用
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休”. - -----华罗庚
