8.3独立性检验课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共14张PPT)
文档属性
| 名称 | 8.3独立性检验课件-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册(共14张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览







文档简介
(共14张PPT)
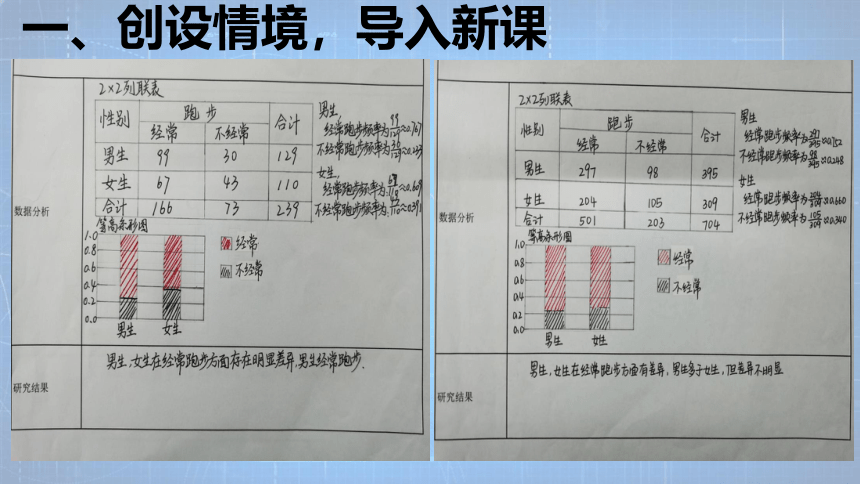
一、创设情境,导入新课
独立性检验
普通高中教科书数学选择性必修第三册人民教育出版社A版
问题1:如何从概率的角度去研究两个分类变量X与Y是否有关呢?
二、探索研究,构建新知
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
H0: 分类变量X和Y独立
二、探索研究,构建新知
问题2:请根据分类变量X与Y独立的定义及等价条件,利用列联表中的数据,构造一个用于推断他们是否独立的统计量?
Karl Pearson (英)于1900年提出的卡方检验是一种具有广泛用途的统计方法。
如果χ2较大,就推断H0不成立,否则认为H0成立。
问题3:判断 χ2 大小的标准是什么?
α 0.1 0.05 0.01 0.005 0.001
χα 2.706 3.841 6.635 7.879 10.828
小概率值α的检验规则:
当 时,我们推断H0不成立,认为X和Y不独立,该推断犯错概率不超过α;
当 时,我们没有充分证据推断H0不成立,可认为X和Y独立。
这种利用 χ2 的取值推断分类变量X和Y是否独立的方法称为χ2 独立性检验,简称独立性检验。
三、例题讲解,巩固新知
例1、(快问快答)对于小概率值α=0.05,请说出以下式子的统计意义。
(1)
(2)
三、例题讲解,巩固新知
例2、依据小概率值α=0.1的 χ2 独立性检验分析前一节中例1的抽样数据,能否据此推断两校学生的数学成绩优秀率有差异?
学校X 数学成绩Y 合计
不优秀(Y=0) 优秀(Y=1)
甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
三、例题讲解,巩固新知
解:
零假设H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异。根据表中的数据,计算得到:
根据小概率值α=0.1的 χ2 独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即两校的数学成绩优秀率无差异。
χ2独立性检验基本步骤:
1. 确定小概率值α;
2. 提出零假设H0 ;
3. 计算χ2,并与小概率值α所对应的临界值作比较 ;
4. 利用小概率值α的检验规则下结论。
三、例题讲解,巩固新知
例3、依据小概率值α=0.01的 χ2 独立性检验,分析性别是否对经常跑步有影响?
独立性检验
思想方法
知识深化
初步应用
独立性检验的基本原理及基本步骤
独立检验与反证法的区别与联系
利用独立性检验解决生活中的问题
四、归纳总结,感悟提高
这节课你感受最深的是什么?
五、课后作业,学以至用
高中生选择历史类还是物理类与性别有关系吗?解决这个问题时,要认真思考以下几个问题:
1、要调查的问题是什么?
2、如何设计抽样方案?
3、如何分析抽样数据?
4、从中能够得出什么规律?发现什么问题?
本节课到此结束
再 见
一、创设情境,导入新课
独立性检验
普通高中教科书数学选择性必修第三册人民教育出版社A版
问题1:如何从概率的角度去研究两个分类变量X与Y是否有关呢?
二、探索研究,构建新知
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
H0: 分类变量X和Y独立
二、探索研究,构建新知
问题2:请根据分类变量X与Y独立的定义及等价条件,利用列联表中的数据,构造一个用于推断他们是否独立的统计量?
Karl Pearson (英)于1900年提出的卡方检验是一种具有广泛用途的统计方法。
如果χ2较大,就推断H0不成立,否则认为H0成立。
问题3:判断 χ2 大小的标准是什么?
α 0.1 0.05 0.01 0.005 0.001
χα 2.706 3.841 6.635 7.879 10.828
小概率值α的检验规则:
当 时,我们推断H0不成立,认为X和Y不独立,该推断犯错概率不超过α;
当 时,我们没有充分证据推断H0不成立,可认为X和Y独立。
这种利用 χ2 的取值推断分类变量X和Y是否独立的方法称为χ2 独立性检验,简称独立性检验。
三、例题讲解,巩固新知
例1、(快问快答)对于小概率值α=0.05,请说出以下式子的统计意义。
(1)
(2)
三、例题讲解,巩固新知
例2、依据小概率值α=0.1的 χ2 独立性检验分析前一节中例1的抽样数据,能否据此推断两校学生的数学成绩优秀率有差异?
学校X 数学成绩Y 合计
不优秀(Y=0) 优秀(Y=1)
甲校(X=0) 33 10 43
乙校(X=1) 38 7 45
合计 71 17 88
三、例题讲解,巩固新知
解:
零假设H0:分类变量X与Y相互独立,即两校学生的数学成绩优秀率无差异。根据表中的数据,计算得到:
根据小概率值α=0.1的 χ2 独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即两校的数学成绩优秀率无差异。
χ2独立性检验基本步骤:
1. 确定小概率值α;
2. 提出零假设H0 ;
3. 计算χ2,并与小概率值α所对应的临界值作比较 ;
4. 利用小概率值α的检验规则下结论。
三、例题讲解,巩固新知
例3、依据小概率值α=0.01的 χ2 独立性检验,分析性别是否对经常跑步有影响?
独立性检验
思想方法
知识深化
初步应用
独立性检验的基本原理及基本步骤
独立检验与反证法的区别与联系
利用独立性检验解决生活中的问题
四、归纳总结,感悟提高
这节课你感受最深的是什么?
五、课后作业,学以至用
高中生选择历史类还是物理类与性别有关系吗?解决这个问题时,要认真思考以下几个问题:
1、要调查的问题是什么?
2、如何设计抽样方案?
3、如何分析抽样数据?
4、从中能够得出什么规律?发现什么问题?
本节课到此结束
再 见
