小学数学六年级下册-第四单元-正比例与反比例(正比例的应用)北师大版(49张PPT)
文档属性
| 名称 | 小学数学六年级下册-第四单元-正比例与反比例(正比例的应用)北师大版(49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 777.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 13:11:31 | ||
图片预览










文档简介
(共49张PPT)
第四章:正比例与反比例
主题:正比例的应用
目录
同步检测
例题点拨
终极突破
课堂练习
01
同步检测
同步检测
1. 比例的两个内项之积减去两个外项之积,差是( )。
同步检测
1. 比例的两个内项之积减去两个外项之积,差是( )。
【答案】
0
同步检测
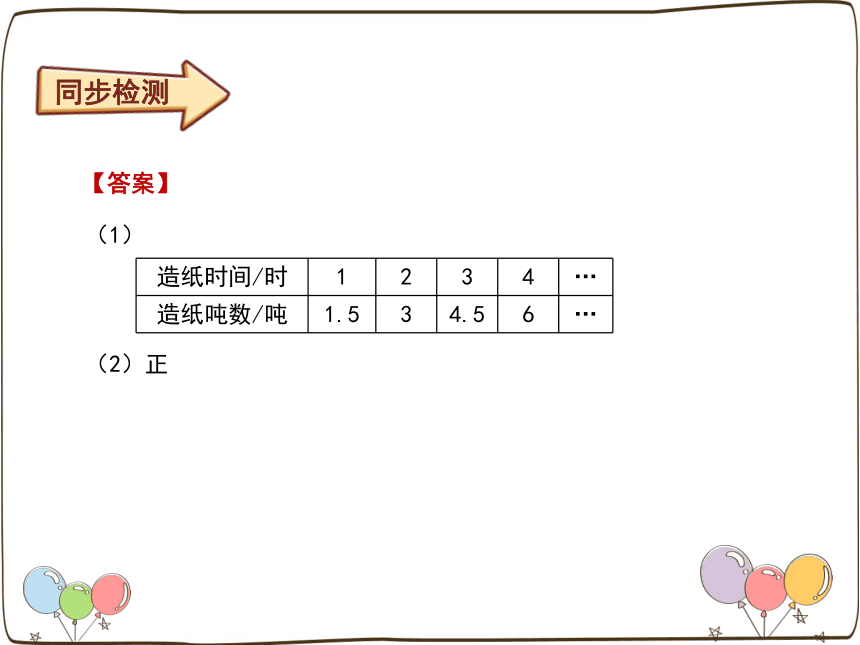
2. 某造纸厂每小时造纸1.5吨,2小时、3小时…各造多少吨纸?
(1)请完成下表格。
(2)造纸吨数与造纸时间成( )比例。
造纸时间/时 1 2 3 4 …
造纸吨数/吨 1.5 …
同步检测
【答案】
(1)
(2)正
造纸时间/时 1 2 3 4 …
造纸吨数/吨 1.5 3 4.5 6 …
02
例题点拨
经典例题
例1
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
例1
【解析】
表格中年龄和体重都在变,因此都是变化量;
从表格可以看出,小明年龄增长的同时,体重也在增长,因此小明的体重在8岁前随着年龄的增长而增长。
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
例1
小明的年龄和体重在发生变化,
小明在8岁前的体重随年龄增长而增长。
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
变式
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
经典例题
变式
【解析】
表格中年龄和身高都在变化,因此都是变量;
从表格中可以看出,随着年龄的增长,小红的身高也在增长,因此,身高随着年龄的增长而增长。
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
经典例题
变式
(1)年龄和身高是变量,
(2)小红在2~7岁身高随年龄增长而增长。
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
技 巧 点 拨
生活中存在着大量的互相依存的变量,一种量变化,另一种量也随着变化,并且这种变化是相互关联的。
经典例题
例2
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40
经典例题
例2
【解析】
生产量=生产速度×时间;
根据所画图像是过原点的直线,因此生产量和时间成正比例关系。
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40 60 80 100 120
经典例题
例2
生产数量如表格所示;
所画图像如图;
生产量和时间成正比例关系。
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40 60 80 100 120
经典例题
变式
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1
经典例题
【解析】
净水量=每小时净水量×时间;
根据所画图像是过原点的直线,可知净水量与时间成正比例关系。
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1 1.5 2 2.5 3
变式
经典例题
净水量如表所示;
图像如图所示;
净水量与时间成正比例关系。
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1 1.5 2 2.5 3
变式
技 巧 点 拨
正比例的两个变量的比值是定值,正比例的图像是一条过原点的直线。
经典例题
例3
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
例3
【解析】
甲、乙一起做,分别生产的零件总数之比与工作效率之比相等,从乙的工作效率可以得到甲的工作效率,求得零件总数,再得到乙做的个数。
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
例3
18×
答:乙一共做了108个。
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
经典例题
【解析】
由于总路程一定,可以得到货车和客车行驶的速度之比,两车从开始到相遇所用的时间相等,因此两车的路程之比就是速度之比。
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
经典例题
50÷(3-2)×(3+2)=250(千米)
答:A、B两地之间距离250千米。
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
技 巧 点 拨
行程问题中,时间一定时,路程与速度成正比例关系。
03
终极突破
提高训练
1.(★) 填空。
(1)成正比例的两个变量中,一个量增大,另一个量就( )。
(2)圆的周长和半径成( )比例关系。
(3)汽车在匀速行驶时,( )和( )成正比例关系。
提高训练
【答案】
(1)增大
(2)正
(3)路程,时间
提高训练
2.(★ )判断下列变量中是否成正比例关系。
(1)每天烧煤量一定,烧煤的总量和烧的天数。 ( )
(2)计划植树的棵数一定,已植棵数和未植棵数。 ( )
(3)要生产的零件总数一定,生产速度和时间。 ( )
(4)出勤率一定,出勤人数和总人数。 ( )
提高训练
【答案】
(1)√
(2)×
(3)×
(4)√
提高训练
3. ( ★ ★ )如图是甲、乙两队修路的进度统计图。根据该图回答问题。(1)甲队和乙队修路的长度与时间成什么关系?为什么?
(2)哪个队修路速度快?为什么?
提高训练
【答案】
(1)甲队和乙队修路的长度与时间成正比例关系,因为甲队和乙队
修路的图像都是过原点的直线。
(2)甲队修路速度快,因为甲队1天修40米,而乙队2天才修40米。
提高训练
4. ( ★ ★ )同一时间、同一地点测量的杆高和影长如下表所示,杆高和影长成什么关系?为什么?
杆高/m 4 6 12 17
影长/m 2.8 4.2 8.4 11.9
提高训练
4.( ★ ★ ) 同一时间、同一地点测量的杆高和影长如下表所示,杆高和影长成什么关系?为什么?
杆高/m 4 6 12 17
影长/m 2.8 4.2 8.4 11.9
【答案】
4:2.8=1:0.7,6:4.2=1:0.7,12:8.4=1:0.7,17:11.9=1:0.7
因此影长是杆高的0.7倍,则杆高和影长成正比例关系。
提高训练
5. ( ★ ★ ★ )小明爸爸开汽车从甲地到乙地,2小时行驶了140千米,照这样的速度行驶,一共花了6小时到达乙地,并且中间休息了一个小时,甲、乙两地之间的距离是多少千米?
提高训练
【答案】
140÷2=70(千米/时)
70×(6-1)=350(千米)
答:甲、乙两地距离350千米。
【解析】
先算出汽车行驶的速度:140÷2=70(千米/时),再算出一共行驶的时间:6-1=5(时),路程=速度×时间,得到甲、乙两地相距的距离。
提高训练
6. ( ★ ★ ★ )某工厂甲、乙两人加工一批零件,甲、乙同时开始做,5个小时后做完,知道甲比乙一共少加工50个零件,甲、乙两人的工作效率之比为4:5,那么甲每小时加工多少个零件?
提高训练
【答案】
甲做的零件数:50÷(5-4)×4=200(个)
甲每小时加工零件个数:200÷5=40(个)
答:甲每小时加工40个零件。
【解析】
由于两个人的工作时间一定,工作总量和工作效率成正比,因此从甲、乙两人的工作总量差,可以得到甲的工作总量,进而可以得到甲的工作效率。
1
总 结
2
3
生活中存在着大量的互相依存的变量,一种量变化,另一种量也随着变化,并且这种变化是相互关联的。
正比例的两个变量的比值是定值,正比例的图像是一条过原点的直线。
行程问题中,时间一定时,路程与速度成正比例关系。
04
课堂练习
1. 判断下列变量是否成正比例关系。
(1)圆柱体的地面直径一定,它的高和侧面积。( )
(2)长方形的长一定,面积和宽。 ( )
(3)路程一定,行驶速度和行驶时间。 ( )
2.下表是水龙头打开后出水量和时间的统计表,已知水的流速不变,请将表格填写完整。
课后作业
时间/秒 4 10
出水量/升 12.8 16 20
3.一个晒盐场用100克的海水,可以晒出3克盐,如果一块盐田一次放入5000吨的海水,可以晒出多少吨盐?
4.车队要向灾区运送1500吨救灾物资,前5小时运到灾区300吨,照这样的速度,剩下的救灾物资还要多少小时才全部运到灾区?
5.下图是甲、乙两个人生产某零件的统计表,红线为甲,黑线为乙,
甲、乙生产6个小时,甲比乙多生产多少个?
课后作业
【答案】
1. (1)√; (2)√; (3)×
2.
3. 解:设可以晒出x吨盐
100:3=5000:x
x=150
答:可以晒出150吨盐。
时间/秒 4 6.4 8 10
出水量/升 8 12.8 16 20
4. 解:剩下的救灾物资还要x小时才全部运到灾区
300:5=(1500-300):x
x=20
答:剩下的救灾物资还要20小时才全部运到灾区。
5. (40-25)×6=90(个)
答:甲比乙多生产90个。
2
0
2
2
Thanks for listening.
Welcome to ask questions
第四章:正比例与反比例
主题:正比例的应用
目录
同步检测
例题点拨
终极突破
课堂练习
01
同步检测
同步检测
1. 比例的两个内项之积减去两个外项之积,差是( )。
同步检测
1. 比例的两个内项之积减去两个外项之积,差是( )。
【答案】
0
同步检测
2. 某造纸厂每小时造纸1.5吨,2小时、3小时…各造多少吨纸?
(1)请完成下表格。
(2)造纸吨数与造纸时间成( )比例。
造纸时间/时 1 2 3 4 …
造纸吨数/吨 1.5 …
同步检测
【答案】
(1)
(2)正
造纸时间/时 1 2 3 4 …
造纸吨数/吨 1.5 3 4.5 6 …
02
例题点拨
经典例题
例1
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
例1
【解析】
表格中年龄和体重都在变,因此都是变化量;
从表格可以看出,小明年龄增长的同时,体重也在增长,因此小明的体重在8岁前随着年龄的增长而增长。
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
例1
小明的年龄和体重在发生变化,
小明在8岁前的体重随年龄增长而增长。
小明用下表记录了他从出生到8岁时的体重变化,问从表中可以看出小明的哪些量在发生变化,小明在8岁前的体重是如何随年龄增长而变化的?
年龄 出生时 2岁 4岁 6岁 8岁
体重/kg 4 15 21 26 30
经典例题
变式
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
经典例题
变式
【解析】
表格中年龄和身高都在变化,因此都是变量;
从表格中可以看出,随着年龄的增长,小红的身高也在增长,因此,身高随着年龄的增长而增长。
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
经典例题
变式
(1)年龄和身高是变量,
(2)小红在2~7岁身高随年龄增长而增长。
小红记录了她7岁之前的身高变化,如下表。
(1)上表中哪些量是变量?
(2)小红2~7岁身高是如何随着年龄的增长而变化的?
年龄 2岁 3岁 4岁 5岁 6岁 7岁
身高/cm 83 92 99 105 110 114
技 巧 点 拨
生活中存在着大量的互相依存的变量,一种量变化,另一种量也随着变化,并且这种变化是相互关联的。
经典例题
例2
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40
经典例题
例2
【解析】
生产量=生产速度×时间;
根据所画图像是过原点的直线,因此生产量和时间成正比例关系。
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40 60 80 100 120
经典例题
例2
生产数量如表格所示;
所画图像如图;
生产量和时间成正比例关系。
某车间生产纸箱,每小时生产20个,请完成下表,并按表描点连线,通过图像判断生产量和时间的关系。
时间/时 1 2 3 4 5 6
数量/个 20 40 60 80 100 120
经典例题
变式
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1
经典例题
【解析】
净水量=每小时净水量×时间;
根据所画图像是过原点的直线,可知净水量与时间成正比例关系。
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1 1.5 2 2.5 3
变式
经典例题
净水量如表所示;
图像如图所示;
净水量与时间成正比例关系。
某净水厂每小时净化水0.5吨,请完成下表并画出图像,并判断净水量与时间的关系。
时间/时 1 2 3 4 5 6
吨数/吨 0.5 1 1.5 2 2.5 3
变式
技 巧 点 拨
正比例的两个变量的比值是定值,正比例的图像是一条过原点的直线。
经典例题
例3
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
例3
【解析】
甲、乙一起做,分别生产的零件总数之比与工作效率之比相等,从乙的工作效率可以得到甲的工作效率,求得零件总数,再得到乙做的个数。
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
例3
18×
答:乙一共做了108个。
生产一批零件,甲单独做要15个小时,乙单独每小时做18个,现在两个人一起做,完成任务时,甲、乙分别生产的零件总数比是2:3,乙一共做了多少个?
经典例题
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
经典例题
【解析】
由于总路程一定,可以得到货车和客车行驶的速度之比,两车从开始到相遇所用的时间相等,因此两车的路程之比就是速度之比。
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
经典例题
50÷(3-2)×(3+2)=250(千米)
答:A、B两地之间距离250千米。
变式
一辆货车从A地开往B地需要4个小时,另一辆客车从B地开往A地需要6个小时,两辆汽车同时相对开始行驶,相遇时货车比客车多行驶了50千米,A、B两地之间距离多少千米?
技 巧 点 拨
行程问题中,时间一定时,路程与速度成正比例关系。
03
终极突破
提高训练
1.(★) 填空。
(1)成正比例的两个变量中,一个量增大,另一个量就( )。
(2)圆的周长和半径成( )比例关系。
(3)汽车在匀速行驶时,( )和( )成正比例关系。
提高训练
【答案】
(1)增大
(2)正
(3)路程,时间
提高训练
2.(★ )判断下列变量中是否成正比例关系。
(1)每天烧煤量一定,烧煤的总量和烧的天数。 ( )
(2)计划植树的棵数一定,已植棵数和未植棵数。 ( )
(3)要生产的零件总数一定,生产速度和时间。 ( )
(4)出勤率一定,出勤人数和总人数。 ( )
提高训练
【答案】
(1)√
(2)×
(3)×
(4)√
提高训练
3. ( ★ ★ )如图是甲、乙两队修路的进度统计图。根据该图回答问题。(1)甲队和乙队修路的长度与时间成什么关系?为什么?
(2)哪个队修路速度快?为什么?
提高训练
【答案】
(1)甲队和乙队修路的长度与时间成正比例关系,因为甲队和乙队
修路的图像都是过原点的直线。
(2)甲队修路速度快,因为甲队1天修40米,而乙队2天才修40米。
提高训练
4. ( ★ ★ )同一时间、同一地点测量的杆高和影长如下表所示,杆高和影长成什么关系?为什么?
杆高/m 4 6 12 17
影长/m 2.8 4.2 8.4 11.9
提高训练
4.( ★ ★ ) 同一时间、同一地点测量的杆高和影长如下表所示,杆高和影长成什么关系?为什么?
杆高/m 4 6 12 17
影长/m 2.8 4.2 8.4 11.9
【答案】
4:2.8=1:0.7,6:4.2=1:0.7,12:8.4=1:0.7,17:11.9=1:0.7
因此影长是杆高的0.7倍,则杆高和影长成正比例关系。
提高训练
5. ( ★ ★ ★ )小明爸爸开汽车从甲地到乙地,2小时行驶了140千米,照这样的速度行驶,一共花了6小时到达乙地,并且中间休息了一个小时,甲、乙两地之间的距离是多少千米?
提高训练
【答案】
140÷2=70(千米/时)
70×(6-1)=350(千米)
答:甲、乙两地距离350千米。
【解析】
先算出汽车行驶的速度:140÷2=70(千米/时),再算出一共行驶的时间:6-1=5(时),路程=速度×时间,得到甲、乙两地相距的距离。
提高训练
6. ( ★ ★ ★ )某工厂甲、乙两人加工一批零件,甲、乙同时开始做,5个小时后做完,知道甲比乙一共少加工50个零件,甲、乙两人的工作效率之比为4:5,那么甲每小时加工多少个零件?
提高训练
【答案】
甲做的零件数:50÷(5-4)×4=200(个)
甲每小时加工零件个数:200÷5=40(个)
答:甲每小时加工40个零件。
【解析】
由于两个人的工作时间一定,工作总量和工作效率成正比,因此从甲、乙两人的工作总量差,可以得到甲的工作总量,进而可以得到甲的工作效率。
1
总 结
2
3
生活中存在着大量的互相依存的变量,一种量变化,另一种量也随着变化,并且这种变化是相互关联的。
正比例的两个变量的比值是定值,正比例的图像是一条过原点的直线。
行程问题中,时间一定时,路程与速度成正比例关系。
04
课堂练习
1. 判断下列变量是否成正比例关系。
(1)圆柱体的地面直径一定,它的高和侧面积。( )
(2)长方形的长一定,面积和宽。 ( )
(3)路程一定,行驶速度和行驶时间。 ( )
2.下表是水龙头打开后出水量和时间的统计表,已知水的流速不变,请将表格填写完整。
课后作业
时间/秒 4 10
出水量/升 12.8 16 20
3.一个晒盐场用100克的海水,可以晒出3克盐,如果一块盐田一次放入5000吨的海水,可以晒出多少吨盐?
4.车队要向灾区运送1500吨救灾物资,前5小时运到灾区300吨,照这样的速度,剩下的救灾物资还要多少小时才全部运到灾区?
5.下图是甲、乙两个人生产某零件的统计表,红线为甲,黑线为乙,
甲、乙生产6个小时,甲比乙多生产多少个?
课后作业
【答案】
1. (1)√; (2)√; (3)×
2.
3. 解:设可以晒出x吨盐
100:3=5000:x
x=150
答:可以晒出150吨盐。
时间/秒 4 6.4 8 10
出水量/升 8 12.8 16 20
4. 解:剩下的救灾物资还要x小时才全部运到灾区
300:5=(1500-300):x
x=20
答:剩下的救灾物资还要20小时才全部运到灾区。
5. (40-25)×6=90(个)
答:甲比乙多生产90个。
2
0
2
2
Thanks for listening.
Welcome to ask questions
