苏科版七年级下册7.1 探索直线平行的条件 课件(共51张PPT)
文档属性
| 名称 | 苏科版七年级下册7.1 探索直线平行的条件 课件(共51张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 22:40:21 | ||
图片预览








文档简介
(共51张PPT)
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
知识点
同位角相等,两直线平行
1
1. 同位角的定义
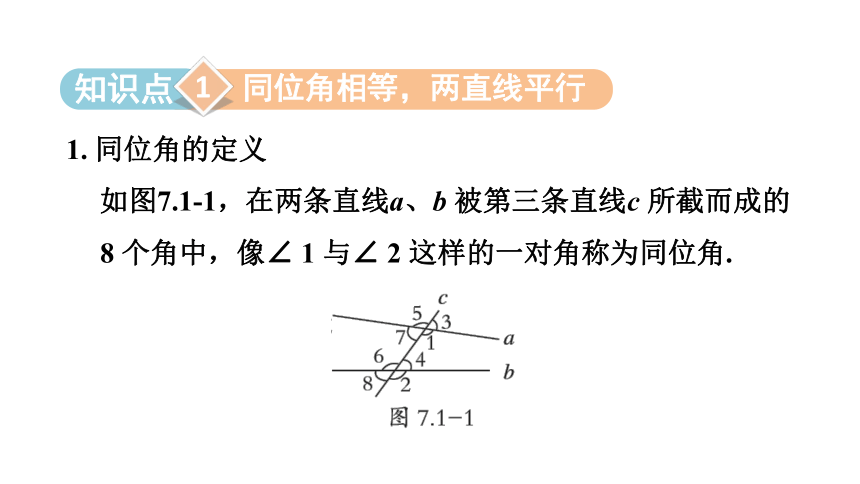
如图7.1-1,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为同位角.
特别提醒:
(1)同位角指的是两个角分别在两条直线的同一方向,并且都在第三条直线的同侧;
● ● ● ●
(2)同位角指的是两个角之间的位置关系,不是大小关系;具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
同位角 在截线同侧,在两条被截直线同一方向 形如字母“F”( 或倒置、反置、旋转)
● ● ● ●
● ● ● ●
(3)两条直线被第三条直线所截,得到的八个角(简称“三线八角”),在“三线八角”中有4 对同位角.
特别解读:
1. 同位角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 同位角的顶点不是公共的.
3. “同”表示“相同”,“位”表示“位置”.“同位角”可理解为“相同位置的两个角”,即如果一个角在左上方,那么另一个角也应在左上方.以此类推,两个同位角的位置关系具有“同上、同左”、“同上、同右”、“同下、同左”、“同下、同右”的特征.
2. 基本事实(平行线的判定方法1)
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.
● ● ● ● ●
特别解读:
(1)构成同位角的两条直线不一定平行, 只有形成的一对同位角相等,这两条直线才平行;
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两条直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁;
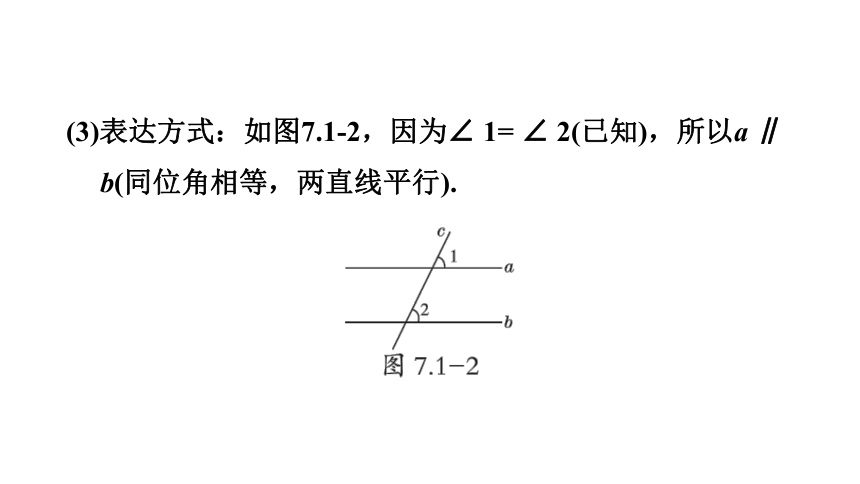
(3)表达方式:如图7.1-2,因为∠ 1= ∠ 2(已知),所以a ∥ b(同位角相等,两直线平行).
例 1
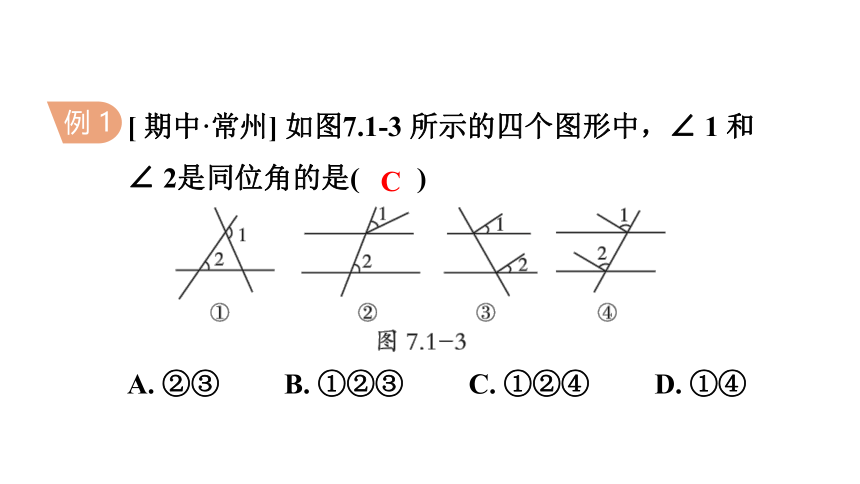
[ 期中·常州] 如图7.1-3 所示的四个图形中,∠ 1 和
∠ 2是同位角的是( )
A. ②③ B. ①②③ C. ①②④ D. ①④
C
解题秘方:紧扣 “同位角”的位置特征逐项进行判断.
解:根据同位角的定义, 最直观的方法是用模型来套, 看它们是否符合“F”形特征. 同时, 也要看它们是不是有一条边在同一直线上, 因为同位角是两条直线被第三条直线所截而成的. 由此可见, ①②④符合同位角的位置特征.
方法点拨:
判断两个角是不是同位角的方法:
首先要看这两个角是不是两条直线被第三条直线所截形成的,即是不是“三线八角”中的两角;其次看这两个角是不是具有不同的顶点;最后看这两个角的位置特征是否满足同位角的位置特征:三边成“F”形.
例2
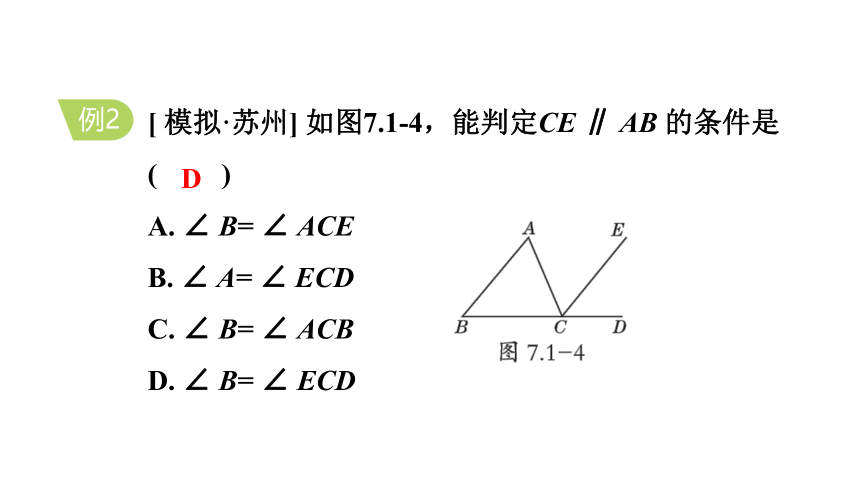
[ 模拟·苏州] 如图7.1-4,能判定CE ∥ AB 的条件是( )
A. ∠ B= ∠ ACE
B. ∠ A= ∠ ECD
C. ∠ B= ∠ ACB
D. ∠ B= ∠ ECD
D
解题秘方:紧扣“同位角相等,两直线平行”,寻找相等的同位角.
解:要想判定CE ∥ AB,可根据“同位角相等, 两直线平行”找相等的同位角, 实质上就是要找以CE 和AB 为边的同位角, 同时兼顾同位角的定义, 它们必有一边在同一直线上,于是从所给的各个选项中筛选可得∠ B= ∠ ECD.
方法点拨:
解答此题的关键是利用两条平行线为角的一边,寻找相等的一对同位角,然后根据平行线的判定方法即可求解,即同位角相等,两直线平行.
例 3
如图7.1-5, 已知AC ⊥ AE,BD ⊥ BF, ∠ 1=15 °,
∠ 2=15°,AE 与BF 平行吗?为什么?
解:AE ∥ BF. 理由如下:
因为AC ⊥ AE,BD ⊥ BF(已知),
所以∠ EAC= ∠ FBD=90°(垂直的定义).
因为∠ 1= ∠ 2(已知),
所以∠ EAC+ ∠ 1= ∠ FBD+ ∠ 2(等式的性质),
即∠ EAB= ∠ FBG.
所以AE ∥ BF(同位角相等, 两直线平行).
解题秘方:要判断AE 与BF 是否平行, 可以看与这两条线相关的同位角是否相等. 注意到已知条件中的AC ⊥ AE,BD ⊥ BF, 有∠ EAC= ∠ FBD=90°. 又因为∠ 1=15°,∠ 2=15°,则可得∠ EAB=
∠ FBG,可由“同位角相等,两直线平行”判断AE ∥ BF.
解法提醒:
判断两条直线是否平行,可通过找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行,否则不平行.
知识点
内错角相等,两直线平行
2
1. 内错角的定义
如图7.1-6,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为内错角.
特别提醒:
(1)内错角指的是两个角都在两条直线之间,并且分别在第三条直线的两侧;
● ●
● ●
(2)内错角指的是两个角之间的位置关系,不是大小关系;具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
内错角 在截线两侧,在两条被截直线之间 形如字母“Z”(或倒置、反置、旋转)
(3)在“三线八角”中,有2 对内错角.
特别解读:
1. 内错角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 内错角的顶点不是公共的.
3. “内”可理解为夹在两条直线之间,“错”可理解为交错,即位于第三条直线的两侧. 内错角的位置关系具有“同内、异侧”的特征.
▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲ ▲
▲
▲
2. 基本事实(平行线的判定方法2)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的;
● ● ● ● ●
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
(3)表达方式:如图7.1-7,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
特别提醒:
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等时,这两条被截线才平行.
例4
如图7.1-8,试找出图中与∠ 2 是同位角、内错角的角.
解:在AF 和AG 被DE 所截的这个基本图形中,可以看出∠ 6 和∠ 2 处于“同一个位置”,因此∠ 2 的同位角为∠ 6. 根据内错角的特征可知∠ 2 和∠ 8 是内错角.
解题秘方:根据同位角及内错角的位置特征进行识别.
解法提醒:
寻找已知角的同位角、内错角时,先要寻找基本图形,即弄清哪条直线是截线,哪两条直线是被截直线,然后利用同位角、内错角的位置特征去寻找符合该特征的角.
▲ ▲
▲ ▲
例 5
[ 模拟·南京] 如图7.1-9,看图填空:
(1)∠ 1 的同位角是______,∠ 1 的内错角是______;
(2)如果∠ 1= ∠ 2,那么___∥___,
根据是______________________;
(3)如果∠ 4= ∠ 5,那么___∥___,
根据是______________________.
∠ 3
∠ 2
DE
BC
内错角相等, 两直线平行
FG
DC
同位角相等, 两直线平行
解题秘方:(1)根据同位角和内错角的定义和位置特征可知,∠ 1 的同位角是∠ 3, ∠ 1 的内错角是∠ 2;
(2)由∠ 1= ∠ 2,根据“内错角相等,两直线平行”有DE ∥ BC;
(3)由∠ 4= ∠ 5,根据“同位角相等,两直线平行”有FG ∥ DC.
方法点拨:
利用内错角相等来判定两直线平行的方法:
(1)看两个角是不是两条直线被第三条直线所截而形成的角;(2)看两个角是不是由上述直线形成的内错角,若是,看其是否相等,若相等,则两条直线平行,否则不平行.
例6
如图7.1-10, 已知∠ ADE=60 °,DF 平分∠ ADE,∠ 1=30°,试说明DF ∥ BE.
解题秘方:先找出DF 和BE 这两条被截线所形成的一对内错角,然后利用条件说明这对内错角相等来判定这两条被截线平行.
解法提醒:
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系.
知识点
同旁内角互补,两直线平行
3
1. 同旁内角的定义
如图7.1-11,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为同旁内角.
特别提醒:
(1)同旁内角指的是两个角都在两条直线之间,且它们都在第三条直线的同一旁;
特别解读:
1. 同旁内角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 同旁内角的顶点不是公共的.
3. 同旁内角的位置关系具有“同内、同侧”的特征.
▲ ▲ ▲ ▲
▲ ▲ ▲
(2)同旁内角指的是两个角之间的位置关系,不是大小关系;
具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
同旁内角 在截线同侧,在两条被截直线之间 形如字母“U”(或倒置、反置、旋转)
(3)在“三线八角”中,有2 对同旁内角.
2. 基本事实(平行线的判定方法3)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
特别解读:
(1)利用同旁内角证明两直线平行时,同旁内角之间的关系是互补,不是相等;
(2)表达方式:如图7.1-12,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
方法点拨:
用数量关系判定两直线平行的方法:
在“三线八角”中,同位角相等、内错角相等、同旁内角互补,只要其中的一个结论成立,再利用对顶角、邻补角等相关知识,可得到其他两个结论也成立.
例 7
[ 期中·无锡] 如图7.1-13,下列结论中错误的是( )
A. ∠ 1 与∠ 2 是同旁内角
B. ∠ 1 与∠ 6 是内错角
C. ∠ 2 与∠ 5 是内错角
D. ∠ 3 与∠ 5 是同位角
C
解题秘方:紧扣同位角、内错角、同旁内角的定义分别判断即可得出结论.
解:根据同位角、内错角、同旁内角的定义逐项分析可知,∠ 1 与∠ 2是同旁内角,∠ 1 与∠ 6 是内错角, ∠ 2 与∠ 5 不是内错角, ∠ 3 与∠ 5 是同位角. 故A、B、D 正确,不合题意; C 错误,符合题意.
方法点拨:
本题运用定义法.识别同位角、内错角、同旁内角的关键是看两个角所涉及的直线是否只有三条,并且有没有一条边在同一条直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征进行判断.
▲ ▲ ▲
例8
如图7.1-14,直线AE、CD 相交于点O,如果∠ A=
110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
解:因为∠ 1= ∠ AOD(对顶角相等), ∠ 1=70°,
所以∠ AOD=70° .
又因为∠ A=110° ,
所以∠ A+ ∠ AOD=180°(等式的性质).
所以AB ∥ CD(同旁内角互补,两直线平行).
解题秘方:由题意可知∠1= ∠AOD=70°,又因为∠A=
110°,所以∠A+∠AOD=180°,故AB ∥ CD.
方法点拨:
本题运用数形结合思想. 平行线的判定是由角之间的数量关系到“形”的判定. 要判定两条直线平行,可围绕截线找同位角、内错角或同旁内角,若同位角相等、内错角相等或同旁内角互补,则两条直线平行.
例 9
如图7.1-15,∠ 1=65°,∠ 2=65°,∠ 3=115°,试说明:
(1)DE ∥ BC;(2)DF ∥ AB. 根据图形,完成下列推理过程:
解:(1)因为∠ 1=65°,∠ 2=65°,所以∠ 1= ∠ 2.
所以____∥_____( ).
(2)因为AB 与DE 相交,∠ 1=65°,
所以∠ 1= ∠ 4=65°( ).
因为∠ 3=115°,
所以∠ 3+ ∠ 4=180° .
所以____∥_____( ).
DE
BC
同位角相等,两直线平行
对顶角相等
DF
AB
同旁内角互补,两直线平行
解题秘方:∠ 1 与∠ 2 是直线DE、BC 被直线AB 所截得到的同位角,所以DE ∥ BC,理由是“同位角相等,两直线平行”. ∠ 1 与∠ 4 是两条直线AB 与DE 相交得到的对顶角,所以∠ 1= ∠ 4,理由是“对顶角相等”. ∠ 3与∠ 4 是直线DF、AB 被直线DE 所截得到的同旁内角,所以DF ∥ AB,理由是“同旁内角互补,两直线平行”.
方法点拨:
例9(1)由两个角相等,判定两条直线平行,其关键是找出两个角是由哪两条直线被哪一条直线所截而形成的角.
例9(2) 是用两角的互补关系来说明两直线平行.
探索直线平行的条件
三线八角
同位角
同旁内角
内错角
两直线平行
的条件
同位角相等,
两直线平行
内错角相等,
两直线平行
同旁内角互补,
两直线平行
7.1 探索直线平行的条件
第7章 平面图形的认识(二)
知识点
同位角相等,两直线平行
1
1. 同位角的定义
如图7.1-1,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为同位角.
特别提醒:
(1)同位角指的是两个角分别在两条直线的同一方向,并且都在第三条直线的同侧;
● ● ● ●
(2)同位角指的是两个角之间的位置关系,不是大小关系;具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
同位角 在截线同侧,在两条被截直线同一方向 形如字母“F”( 或倒置、反置、旋转)
● ● ● ●
● ● ● ●
(3)两条直线被第三条直线所截,得到的八个角(简称“三线八角”),在“三线八角”中有4 对同位角.
特别解读:
1. 同位角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 同位角的顶点不是公共的.
3. “同”表示“相同”,“位”表示“位置”.“同位角”可理解为“相同位置的两个角”,即如果一个角在左上方,那么另一个角也应在左上方.以此类推,两个同位角的位置关系具有“同上、同左”、“同上、同右”、“同下、同左”、“同下、同右”的特征.
2. 基本事实(平行线的判定方法1)
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.
● ● ● ● ●
特别解读:
(1)构成同位角的两条直线不一定平行, 只有形成的一对同位角相等,这两条直线才平行;
(2)“同位角相等,两直线平行”是通过两个同位角的大小关系(相等)推导出两条直线的位置关系(平行). 它是构建起角的大小关系与直线的位置关系的桥梁;
(3)表达方式:如图7.1-2,因为∠ 1= ∠ 2(已知),所以a ∥ b(同位角相等,两直线平行).
例 1
[ 期中·常州] 如图7.1-3 所示的四个图形中,∠ 1 和
∠ 2是同位角的是( )
A. ②③ B. ①②③ C. ①②④ D. ①④
C
解题秘方:紧扣 “同位角”的位置特征逐项进行判断.
解:根据同位角的定义, 最直观的方法是用模型来套, 看它们是否符合“F”形特征. 同时, 也要看它们是不是有一条边在同一直线上, 因为同位角是两条直线被第三条直线所截而成的. 由此可见, ①②④符合同位角的位置特征.
方法点拨:
判断两个角是不是同位角的方法:
首先要看这两个角是不是两条直线被第三条直线所截形成的,即是不是“三线八角”中的两角;其次看这两个角是不是具有不同的顶点;最后看这两个角的位置特征是否满足同位角的位置特征:三边成“F”形.
例2
[ 模拟·苏州] 如图7.1-4,能判定CE ∥ AB 的条件是( )
A. ∠ B= ∠ ACE
B. ∠ A= ∠ ECD
C. ∠ B= ∠ ACB
D. ∠ B= ∠ ECD
D
解题秘方:紧扣“同位角相等,两直线平行”,寻找相等的同位角.
解:要想判定CE ∥ AB,可根据“同位角相等, 两直线平行”找相等的同位角, 实质上就是要找以CE 和AB 为边的同位角, 同时兼顾同位角的定义, 它们必有一边在同一直线上,于是从所给的各个选项中筛选可得∠ B= ∠ ECD.
方法点拨:
解答此题的关键是利用两条平行线为角的一边,寻找相等的一对同位角,然后根据平行线的判定方法即可求解,即同位角相等,两直线平行.
例 3
如图7.1-5, 已知AC ⊥ AE,BD ⊥ BF, ∠ 1=15 °,
∠ 2=15°,AE 与BF 平行吗?为什么?
解:AE ∥ BF. 理由如下:
因为AC ⊥ AE,BD ⊥ BF(已知),
所以∠ EAC= ∠ FBD=90°(垂直的定义).
因为∠ 1= ∠ 2(已知),
所以∠ EAC+ ∠ 1= ∠ FBD+ ∠ 2(等式的性质),
即∠ EAB= ∠ FBG.
所以AE ∥ BF(同位角相等, 两直线平行).
解题秘方:要判断AE 与BF 是否平行, 可以看与这两条线相关的同位角是否相等. 注意到已知条件中的AC ⊥ AE,BD ⊥ BF, 有∠ EAC= ∠ FBD=90°. 又因为∠ 1=15°,∠ 2=15°,则可得∠ EAB=
∠ FBG,可由“同位角相等,两直线平行”判断AE ∥ BF.
解法提醒:
判断两条直线是否平行,可通过找出这两条直线被第三条直线所截得到的一对同位角,并利用相关角的条件判断其是否相等,如果相等,那么这两条直线平行,否则不平行.
知识点
内错角相等,两直线平行
2
1. 内错角的定义
如图7.1-6,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为内错角.
特别提醒:
(1)内错角指的是两个角都在两条直线之间,并且分别在第三条直线的两侧;
● ●
● ●
(2)内错角指的是两个角之间的位置关系,不是大小关系;具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
内错角 在截线两侧,在两条被截直线之间 形如字母“Z”(或倒置、反置、旋转)
(3)在“三线八角”中,有2 对内错角.
特别解读:
1. 内错角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 内错角的顶点不是公共的.
3. “内”可理解为夹在两条直线之间,“错”可理解为交错,即位于第三条直线的两侧. 内错角的位置关系具有“同内、异侧”的特征.
▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲
▲ ▲ ▲ ▲ ▲ ▲
▲
▲
2. 基本事实(平行线的判定方法2)
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
特别解读:(1)“内错角相等,两直线平行”是利用“对顶角相等”和“同位角相等,两直线平行”推导得出的;
● ● ● ● ●
(2)利用“内错角相等”来确定“两直线平行”的关键是弄清这对内错角是哪两条直线被第三条直线所截得到的内错角,再说明这两条直线平行.
(3)表达方式:如图7.1-7,
因为∠ 1= ∠ 2(已知),
所以a ∥ b(内错角相等,两直线平行).
特别提醒:
构成内错角的两条被截线不一定平行,只有形成的一对内错角相等时,这两条被截线才平行.
例4
如图7.1-8,试找出图中与∠ 2 是同位角、内错角的角.
解:在AF 和AG 被DE 所截的这个基本图形中,可以看出∠ 6 和∠ 2 处于“同一个位置”,因此∠ 2 的同位角为∠ 6. 根据内错角的特征可知∠ 2 和∠ 8 是内错角.
解题秘方:根据同位角及内错角的位置特征进行识别.
解法提醒:
寻找已知角的同位角、内错角时,先要寻找基本图形,即弄清哪条直线是截线,哪两条直线是被截直线,然后利用同位角、内错角的位置特征去寻找符合该特征的角.
▲ ▲
▲ ▲
例 5
[ 模拟·南京] 如图7.1-9,看图填空:
(1)∠ 1 的同位角是______,∠ 1 的内错角是______;
(2)如果∠ 1= ∠ 2,那么___∥___,
根据是______________________;
(3)如果∠ 4= ∠ 5,那么___∥___,
根据是______________________.
∠ 3
∠ 2
DE
BC
内错角相等, 两直线平行
FG
DC
同位角相等, 两直线平行
解题秘方:(1)根据同位角和内错角的定义和位置特征可知,∠ 1 的同位角是∠ 3, ∠ 1 的内错角是∠ 2;
(2)由∠ 1= ∠ 2,根据“内错角相等,两直线平行”有DE ∥ BC;
(3)由∠ 4= ∠ 5,根据“同位角相等,两直线平行”有FG ∥ DC.
方法点拨:
利用内错角相等来判定两直线平行的方法:
(1)看两个角是不是两条直线被第三条直线所截而形成的角;(2)看两个角是不是由上述直线形成的内错角,若是,看其是否相等,若相等,则两条直线平行,否则不平行.
例6
如图7.1-10, 已知∠ ADE=60 °,DF 平分∠ ADE,∠ 1=30°,试说明DF ∥ BE.
解题秘方:先找出DF 和BE 这两条被截线所形成的一对内错角,然后利用条件说明这对内错角相等来判定这两条被截线平行.
解法提醒:
要判定两直线平行可以通过说明同位角相等或内错角相等来实现,至于到底选用同位角还是选用内错角,要看具体的题目,要尽可能与已知条件联系.
知识点
同旁内角互补,两直线平行
3
1. 同旁内角的定义
如图7.1-11,在两条直线a、b 被第三条直线c 所截而成的8 个角中,像∠ 1 与∠ 2 这样的一对角称为同旁内角.
特别提醒:
(1)同旁内角指的是两个角都在两条直线之间,且它们都在第三条直线的同一旁;
特别解读:
1. 同旁内角是成对出现的,并且是由三条直线形成的,即一对边共线,另一对边不共线.
2. 同旁内角的顶点不是公共的.
3. 同旁内角的位置关系具有“同内、同侧”的特征.
▲ ▲ ▲ ▲
▲ ▲ ▲
(2)同旁内角指的是两个角之间的位置关系,不是大小关系;
具体特征如下表:
角的名称 位置特征 基本图形 图形的结构体征
同旁内角 在截线同侧,在两条被截直线之间 形如字母“U”(或倒置、反置、旋转)
(3)在“三线八角”中,有2 对同旁内角.
2. 基本事实(平行线的判定方法3)
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
特别解读:
(1)利用同旁内角证明两直线平行时,同旁内角之间的关系是互补,不是相等;
(2)表达方式:如图7.1-12,
因为∠ 1+ ∠ 2=180°(已知),
所以a ∥ b(同旁内角互补,两直线平行).
方法点拨:
用数量关系判定两直线平行的方法:
在“三线八角”中,同位角相等、内错角相等、同旁内角互补,只要其中的一个结论成立,再利用对顶角、邻补角等相关知识,可得到其他两个结论也成立.
例 7
[ 期中·无锡] 如图7.1-13,下列结论中错误的是( )
A. ∠ 1 与∠ 2 是同旁内角
B. ∠ 1 与∠ 6 是内错角
C. ∠ 2 与∠ 5 是内错角
D. ∠ 3 与∠ 5 是同位角
C
解题秘方:紧扣同位角、内错角、同旁内角的定义分别判断即可得出结论.
解:根据同位角、内错角、同旁内角的定义逐项分析可知,∠ 1 与∠ 2是同旁内角,∠ 1 与∠ 6 是内错角, ∠ 2 与∠ 5 不是内错角, ∠ 3 与∠ 5 是同位角. 故A、B、D 正确,不合题意; C 错误,符合题意.
方法点拨:
本题运用定义法.识别同位角、内错角、同旁内角的关键是看两个角所涉及的直线是否只有三条,并且有没有一条边在同一条直线(截线)上,如果没有,就不是;如果有,再根据角的位置特征进行判断.
▲ ▲ ▲
例8
如图7.1-14,直线AE、CD 相交于点O,如果∠ A=
110°,∠ 1=70°,就可以说明AB ∥ CD,这是为什么?
解:因为∠ 1= ∠ AOD(对顶角相等), ∠ 1=70°,
所以∠ AOD=70° .
又因为∠ A=110° ,
所以∠ A+ ∠ AOD=180°(等式的性质).
所以AB ∥ CD(同旁内角互补,两直线平行).
解题秘方:由题意可知∠1= ∠AOD=70°,又因为∠A=
110°,所以∠A+∠AOD=180°,故AB ∥ CD.
方法点拨:
本题运用数形结合思想. 平行线的判定是由角之间的数量关系到“形”的判定. 要判定两条直线平行,可围绕截线找同位角、内错角或同旁内角,若同位角相等、内错角相等或同旁内角互补,则两条直线平行.
例 9
如图7.1-15,∠ 1=65°,∠ 2=65°,∠ 3=115°,试说明:
(1)DE ∥ BC;(2)DF ∥ AB. 根据图形,完成下列推理过程:
解:(1)因为∠ 1=65°,∠ 2=65°,所以∠ 1= ∠ 2.
所以____∥_____( ).
(2)因为AB 与DE 相交,∠ 1=65°,
所以∠ 1= ∠ 4=65°( ).
因为∠ 3=115°,
所以∠ 3+ ∠ 4=180° .
所以____∥_____( ).
DE
BC
同位角相等,两直线平行
对顶角相等
DF
AB
同旁内角互补,两直线平行
解题秘方:∠ 1 与∠ 2 是直线DE、BC 被直线AB 所截得到的同位角,所以DE ∥ BC,理由是“同位角相等,两直线平行”. ∠ 1 与∠ 4 是两条直线AB 与DE 相交得到的对顶角,所以∠ 1= ∠ 4,理由是“对顶角相等”. ∠ 3与∠ 4 是直线DF、AB 被直线DE 所截得到的同旁内角,所以DF ∥ AB,理由是“同旁内角互补,两直线平行”.
方法点拨:
例9(1)由两个角相等,判定两条直线平行,其关键是找出两个角是由哪两条直线被哪一条直线所截而形成的角.
例9(2) 是用两角的互补关系来说明两直线平行.
探索直线平行的条件
三线八角
同位角
同旁内角
内错角
两直线平行
的条件
同位角相等,
两直线平行
内错角相等,
两直线平行
同旁内角互补,
两直线平行
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
