人教课标版(B版)高中数学必修5《等差数列的前n项和:概念和基本运算》名师课件2(共16张PPT)
文档属性
| 名称 | 人教课标版(B版)高中数学必修5《等差数列的前n项和:概念和基本运算》名师课件2(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
等差数列的前n项和
----第一课时
数列{an}的前n项和的定义:
Sn= a1+ a2 + a3 + … +an-2+an-1+an
叫做数列 的前n项和。
等差数列:
公 差 :
通项公式:
等差中项:
重要性质:
高斯,(1777—1855) 德国著名数学家。
1+2+3+…+98+99+100=?
高斯10岁时曾很快算出这一结果,如何算的呢?
我们先看下面的问题。
注意:这里m,n,p,q N*
an+1-an=d(常数)
d
an=a1+(n-1)d
2A=a+b
(1)an=am+(n-m)d
(2)当m+n=p+q时, am+an=ap+aq
1
*
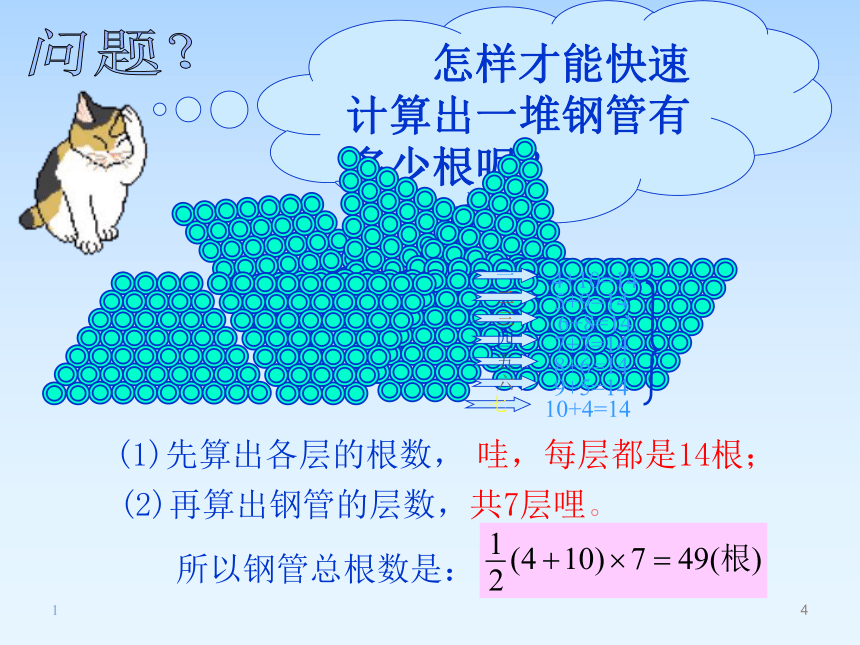
怎样才能快速计算出一堆钢管有多少根呢?
一
二
4+10=14
三
5+9=14
6+8=14
四
7+7=14
五
8+6=14
六
9+5=14
七
10+4=14
(1)先算出各层的根数,
哇,每层都是14根;
(2)再算出钢管的层数,共7层哩。
所以钢管总根数是:
1+2+3+···+100=
高斯,(1777—1855) 德国著名数学家。
问题:
如果把两式左右两端相加,将会有什么结果?
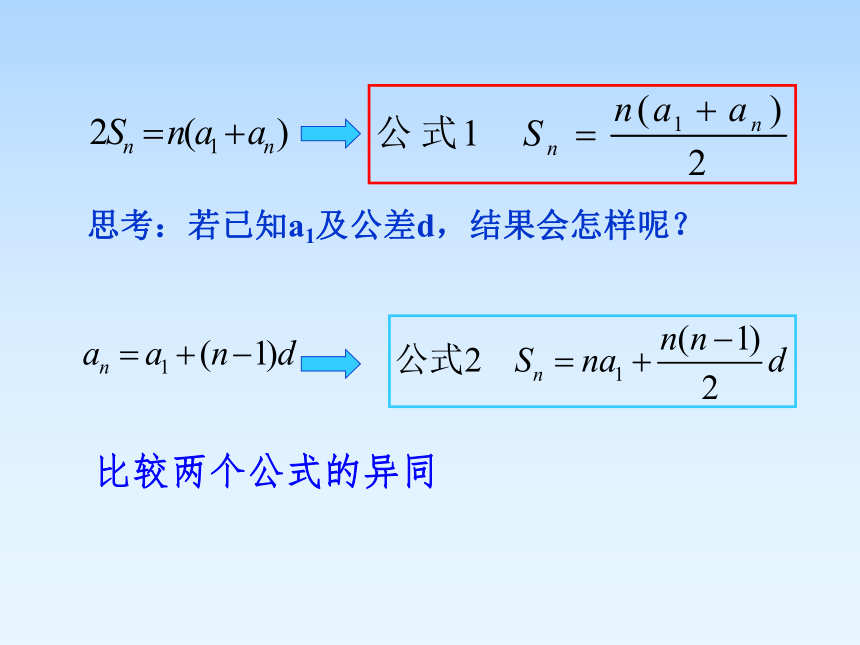
等差数列的前n项和公式
思考:若已知a1及公差d,结果会怎样呢?
比较两个公式的异同
公式结构:
首项
等差数列的前n项和公式的运用
例1 根据下列条件,求相应的等差数列 的
想一想
在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量
结论:知 三 求 二
解题思路一般是:建立方程(组)求解
1.等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差
d=___
2.等差数列{an}中,S10=120,那么a1+a10的值是___
当堂检测
D
-2
24
2.根据等差数列前n项和,求通项公式.
1. 等差数列前n项和公式.
等差数列的前n项和
----第一课时
数列{an}的前n项和的定义:
Sn= a1+ a2 + a3 + … +an-2+an-1+an
叫做数列 的前n项和。
等差数列:
公 差 :
通项公式:
等差中项:
重要性质:
高斯,(1777—1855) 德国著名数学家。
1+2+3+…+98+99+100=?
高斯10岁时曾很快算出这一结果,如何算的呢?
我们先看下面的问题。
注意:这里m,n,p,q N*
an+1-an=d(常数)
d
an=a1+(n-1)d
2A=a+b
(1)an=am+(n-m)d
(2)当m+n=p+q时, am+an=ap+aq
1
*
怎样才能快速计算出一堆钢管有多少根呢?
一
二
4+10=14
三
5+9=14
6+8=14
四
7+7=14
五
8+6=14
六
9+5=14
七
10+4=14
(1)先算出各层的根数,
哇,每层都是14根;
(2)再算出钢管的层数,共7层哩。
所以钢管总根数是:
1+2+3+···+100=
高斯,(1777—1855) 德国著名数学家。
问题:
如果把两式左右两端相加,将会有什么结果?
等差数列的前n项和公式
思考:若已知a1及公差d,结果会怎样呢?
比较两个公式的异同
公式结构:
首项
等差数列的前n项和公式的运用
例1 根据下列条件,求相应的等差数列 的
想一想
在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量
结论:知 三 求 二
解题思路一般是:建立方程(组)求解
1.等差数列{an}的前n项和为Sn,且S3=6,a1=4,则公差
d=___
2.等差数列{an}中,S10=120,那么a1+a10的值是___
当堂检测
D
-2
24
2.根据等差数列前n项和,求通项公式.
1. 等差数列前n项和公式.
