2021-2022学年鲁教版(五四制)六年级数学下册第七章第3节 平行线的性质 专题训练(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)六年级数学下册第七章第3节 平行线的性质 专题训练(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 446.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 08:44:27 | ||
图片预览




文档简介
平行线的性质专题训练
一、探究学习 (问题导引探究)
探究 平行线的性质
素养探究:如果两条直线平行,那么同位角、内错角、同旁内角各有什么关系?
知识导引:
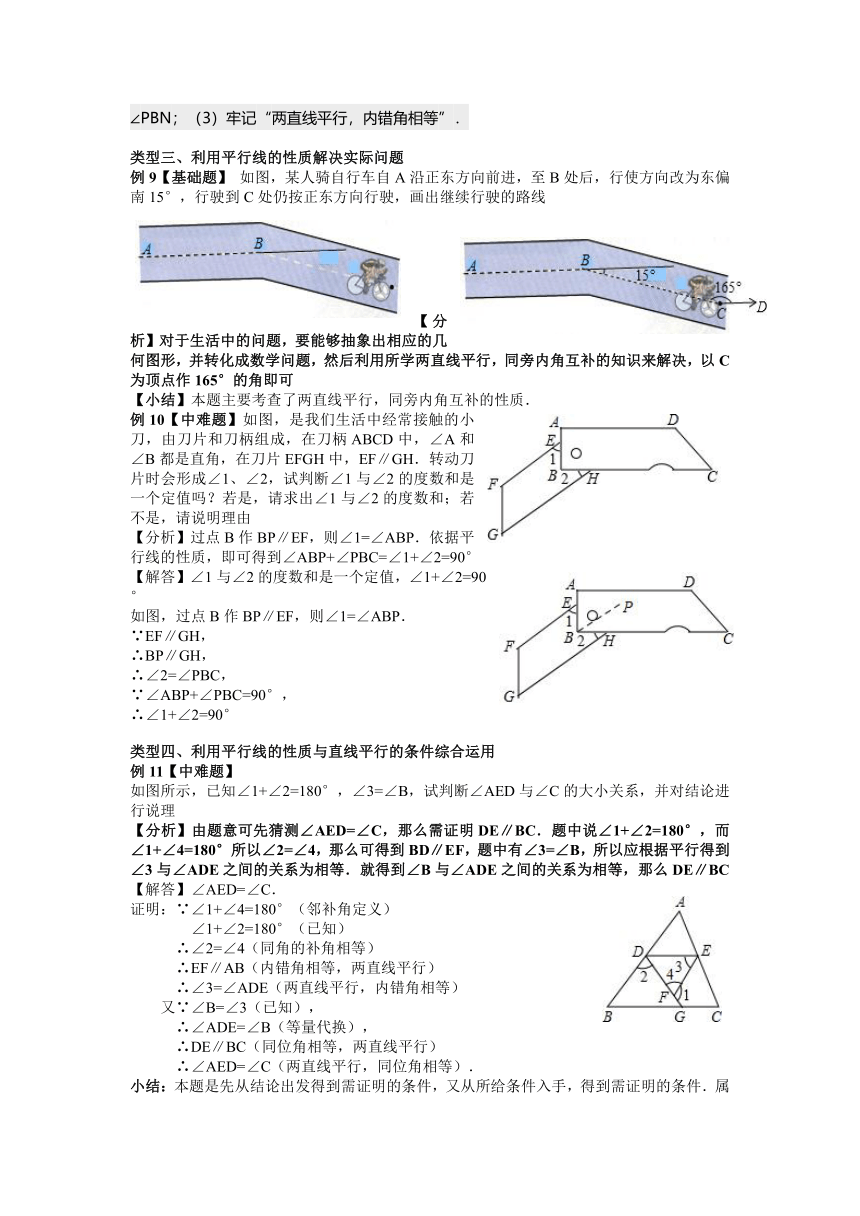
平等线的性质
直线平行与性质之间的关系
例1 【基础题】 如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F
【分析】平行 角相等 (等量代换)角相等
平行线的性质是由“性质关系”得到“数量关系”,直线平行的条件是由“数量关系”得到“位置关系”。直接利用平行线的性质得出∠ABC=∠DCF,再利用已知得出∠E=∠F.
【证明】∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC
∴∠ADC=∠DCF.
∴DE∥BF.
∴∠E=∠F.
小结:此题主要考查了平行线的判定与性质,正确得出∠ADC=∠DCF是解题关键.
例2 【基础题】
【分析】 三个小题都是已知两线段平行和∠1的度数,求∠2的度数。在应用两直线平行的条件和平行线的性质时,一般使用同位角、内错角相等和同旁内角互补,如果已知不是的时候,可以借助对顶角等特殊角的性质将其转化为上述三种类型的角。
二、解题指导 (思路决定成败)
类型一、利用平行线的性质进行角的度数计算
例3 【中难题】如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.(1)若AC⊥AB,∠1=54°49′.求∠2的度数;2)请说明∠ABC+∠BCA+∠CAB=180°.
【分析】(1)依据直线a∥b,AC⊥AB,即可得到∠2=90°-∠3=35°11′;
(2)利用平行线的性质定理可得结论。
【解答】(1)如图,
∵直线a∥b,
∴∠3=∠1=54°49′,
又∵AC⊥AB,
∴∠2=90°-∠3=35°11′;
(2)∵a∥b,
∴∠ACB=∠3,
∠ABC=∠4,
∵∠4+∠3+∠BAC=180°,
∴∠ABC+∠BCA+∠CAB=180°.
小结:本题主要考查平行线的性质了平行线的性质定理,解题的关键是掌握:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.解题过程还需准确掌握度分秒的换算和垂线的定义。
例4【中难题】如图,AB∥CD,EF⊥AB于O,∠FGD=140°,求∠EFG的度数.
【分析】过点F作FM∥AB,则FM∥CD,利用“两直线平行,同旁内角互补”可求出∠MFG的度数,由EF⊥AB可得出∠BOF=90°,结合FM∥AB可求出∠OFM的度数,再利用∠EFG=∠OFM+∠MFG即可求出∠EFG的度数.
【解答】过点F作FM∥AB,如图所示.
∵AB∥CD,FM∥AB,
∴FM∥CD,
∴∠MFG=180°-∠FGD=180°-140°=40°.
∵EF⊥AB,
∴∠BOF=90°,
又∵FM∥AB,
∴∠OFM=180°-∠BOF=180°-90°=90°,
∴∠EFG=∠OFM+∠MFG=90°+40°=130°.
小结:本题考查了平行线的性质以及垂线,牢记“两直线平行,同旁内角互补”是解题关键
例5【中难题】 如图把一个含有30°角的直角三角板的直角顶点A放在直线a上,a∥b,B、C两点在平面上移动,请根据如下条件解答:
(1)如图1,若点C在直线b上,点B在直线b的下方,∠2=20°,则∠1=40°;
(2)如图2,若点C在平行直线a,b内部,点B在直线b的下方,∠2=n°,求∠1度数.
【分析】由含有30°的直角三角板可知∠ACB=60°.
(1)根据平行线的性质可得∠1=∠3,由∠2+∠3=∠ACB=60°,∠2=20°,可求解∠1的度数;
(2)过点C作直线c∥a,根据平行线的性质可得∠1=∠4,再判定c∥b,可得∠2=∠5,由∠ACB=60°,可求解∠1+∠2=60°,利用∠2=n°,即可求出∠1的度数
【解答】由题意可知:∠BAC=90°,∠B=30°,则∠ACB=60°.
(1)如图1,∵a∥b,
∴∠1=∠3,
∵∠2+∠3=∠ACB=60°, ∠2=20°,
∴∠3=40°,
(2)如图2,过C作c∥a,
∴∠1=∠4,
∵a∥b,
∴c∥b,
∴∠2=∠5,
∵∠4+∠5=∠ACB=60°,
∴∠1+∠2=60°,
∵∠2=n°,
∴∠1=(60-n)°.
【小结】本题主要考查平行线的性质与判定,三角形的内角和定理,要能从直角三角板求解∠ACB=60°,关注此类题辅助线的画法
例6【中难题】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2-∠1=16°
【分析】先利用平行线的性质得∠2=∠DEG,∠EFG=∠DEF=49°,再根据折叠的性质得∠DEF=∠GEF=49°,所以∠2=98°,接着利用互补计算出∠1,然后计算∠2-∠1
【解答】∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°-98°=82°,
∴∠2-∠1=98°-82°=16°
【小结】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质
类型二、利用平行线的性质探究角的关系
例7【中难题】如图,已知AB∥CD,AE∥CF,求证:∠BAE=∠DCF
【分析】根据两直线平行,内错角相等的性质以及角的和差关系可证明
【证明】:∵AB∥CD,
∴∠BAC=∠DCA.(两直线平行,内错角相等)
∵AE∥CF,
∴∠EAC=∠FCA.(两直线平行,内错角相等)
∵∠BAC=∠BAE+∠EAC,∠DCA=∠DCF+∠FCA,
∴∠BAE=∠DCF
小结:重点考查了两直线平行,内错角相等的这一性质
例8【中难题】如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
【分析】(1)由AM∥BN,利用“两直线平行,同旁内角互补”可求出∠ABN的度数;
(2)由BC平分∠ABP,BD平分∠PBN,利用角平分线的定义可得出∠CBP=∠ABP,∠PBD=∠PBN,再结合∠CBD=∠CBP+∠PBD即可求出∠CBD的度数;
(3)由AM∥BN,利用“两直线平行,内错角相等”可得出 ∠APB=∠PBN,∠ADB=∠DBN,结合角平分线的定义可得出∠APB=2∠ADB.
【解答】(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°-∠A=180°-60°=120°.
(2)∵BC平分∠ABP,BD平分∠PBN,
∴∠CBP=∠ABP,∠PBD=∠PBN
∴∠CBD=∠CBP+∠PBD=∠ABP+∠PBN=∠ABN=60°.
(3)不变,∠APB=2∠ADB,理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PDN, ∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
小结:本题考查了平行线的性质以及角平分线的定义,解题的关键是:(1)牢记“两直线平行,同旁内角互补”;(2)利用角平分线的定义,找出∠CBP=∠ABP,∠PBD=
∠PBN;(3)牢记“两直线平行,内错角相等”.
类型三、利用平行线的性质解决实际问题
例9【基础题】 如图,某人骑自行车自A沿正东方向前进,至B处后,行使方向改为东偏南15°,行驶到C处仍按正东方向行驶,画出继续行驶的路线
【分析】对于生活中的问题,要能够抽象出相应的几何图形,并转化成数学问题,然后利用所学两直线平行,同旁内角互补的知识来解决,以C为顶点作165°的角即可
【小结】本题主要考查了两直线平行,同旁内角互补的性质.
例10【中难题】如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由
【分析】过点B作BP∥EF,则∠1=∠ABP.依据平行线的性质,即可得到∠ABP+∠PBC=∠1+∠2=90°
【解答】∠1与∠2的度数和是一个定值,∠1+∠2=90°
如图,过点B作BP∥EF,则∠1=∠ABP.
∵EF∥GH,
∴BP∥GH,
∴∠2=∠PBC,
∵∠ABP+∠PBC=90°,
∴∠1+∠2=90°
类型四、利用平行线的性质与直线平行的条件综合运用
例11【中难题】
如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理
【分析】由题意可先猜测∠AED=∠C,那么需证明DE∥BC.题中说∠1+∠2=180°,而∠1+∠4=180°所以∠2=∠4,那么可得到BD∥EF,题中有∠3=∠B,所以应根据平行得到∠3与∠ADE之间的关系为相等.就得到∠B与∠ADE之间的关系为相等,那么DE∥BC
【解答】∠AED=∠C.
证明:∵∠1+∠4=180°(邻补角定义)
∠1+∠2=180°(已知)
∴∠2=∠4(同角的补角相等)
∴EF∥AB(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
又∵∠B=∠3(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等).
小结:本题是先从结论出发得到需证明的条件,又从所给条件入手,得到需证明的条件.属于典型的从两头往中间证明
例12【中难题】如图,已知AD⊥BC,EF⊥BC,垂足分别是D、F.∠1=∠2,∠3=100°,试求∠BAC的度数
【分析】根据平行线的判定与性质可求得∠CGD=80°,∠B=∠GDC,再结合三角形的内角和定理可求解∠BAC的度数
【解答】∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,∠1+∠B=90°,∠2+∠GDC=90°,
∵∠1=∠2,∠3=100°,
∴∠CGD=80°,∠B=∠GDC,
∵∠DGC+∠C+∠GDC=180°,
∴∠B+∠C=100°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-(∠B+∠C)=180°-100°=80°,
故∠BAC的度数为80°
小结:本题主要考查三角形的内角和定理,垂线的定义,平行线的性质等知识的综合运用
【综合法与分析法】几何推理的方法主要有两种:一种是综合法,即由“因”导“果”,由已知条件逐步推到出结论,;另一种是分析法,即执“果”索“因”,根据要推出的结论,找到所需的条件,一步一步倒推,逐渐靠近已知条件。解答时一般用综合法,分析问题市一般用分析法,有时也可以综合应用两种方法。
类型五、分类讨论
例13【基础题】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.
解:如图:
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB-∠PAB,
∴∠APC=∠PCD-∠PAB
【分析—辅助线法】两条平行线之间存在拐点时,通常过拐点作平行线,构造出同位角、内错角、同旁内角,为应用平行线的性质创造条件。
例14【拓展题】已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,过点E作EH∥AB,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(2)如图2,类比(1)中的方法,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(3)如图3,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,直接写出∠PFQ度数.
【分析】从拐点作出平行线(1)证出AB∥EH∥CD,由平行线的性质∠APE=∠PEH,∠CQE=∠QEH.进而得出结论;
(2)证出AB∥EG∥CD,由平行线的性质得∠APE+∠PEG=180°,∠CQE+∠QEG=180°,进而得出结论;
(3)由(2)得∠PEQ+∠BPE+∠EQD=360°,求出∠BPE+∠EQD=220°,由角平分线定义得∠BPF+∠DQF=∠BPE+∠EQD)=110°,由(1)得∠PFQ=∠BPF+∠DQF=110°
解:(1)∠PEQ=∠APE+∠CQE,理由如下:
∵AB∥CD,EH∥AB,
∴AB∥EH∥CD,
∴∠APE=∠PEH,∠CQE=∠QEH.
∵∠PEQ=∠PEH+∠QEH,
∴∠PEQ=∠APE+∠CQE.
(2)∠APE+∠CQE+∠PEQ=360°;理由如下:
过点E作EG∥AB,如图2所示:
∵AB∥CD,EG∥AB,
∴AB∥EG∥CD,
∴∠APE+∠PEG=180°,∠CQE+∠QEG=180°,
∴∠APE+∠PEG+∠CQE+∠QEG=360°,
即∠APE+∠CQE+∠PEQ=360°;
小结:在拐点作已知平行线的平行线就本节常见题型,掌握技巧,才能更好解决问题。
细观察,找规律.
例15 、下列各图中的MA1与NAn平行.
①图①中的∠A1+∠A2=180度.
②图②中的∠A1+∠A2+∠A3=360度.
③图③中的∠A1+∠A2+∠A3+∠A4=540度.
④图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720度.
⑤第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=1800度.
⑥第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n度.
下列各图中AB∥CD.
①图甲中∠B、∠C、∠BEC的数量关系是∠B+∠C=∠BEC.
②图乙中∠B,∠E,∠G,∠F,∠C的数量关系是∠B+∠EGF+∠C=∠E+∠F.
③图丙中∠B,∠E,∠F,∠G,∠H,∠M,∠C的数量关系是
∠B+∠EFG+∠GHM+∠C=∠E+∠G+∠M.
【分析】(1)通过作平行线,由平行线的性质可逐题求解,注意找规律;
【解答】解:(1)∵MA1∥NA2, ∴∠A1+∠A2=180°;
过A2作A2P∥MA1,
∵MA1∥NA3, ∴A2P∥NA3,
∴∠A1+∠A2+∠A3=2×180°=360°;
过A2作A2P∥MA1,过A3作A3Q∥MA1,
∵MA1∥NA4, ∴A2P∥MA1∥A3Q∥NA4,
∴∠A1+∠A2+∠A3+∠A4=3×180°=540°;
过A2作A2P∥MA1,过A3作A3Q∥MA1,过A4作A4B∥MA1,
∵MA1∥NA5, ∴A2P∥MA1∥A3Q∥A4B∥NA5,
∴∠A1+∠A2+∠A3+∠A4+∠A5=4×180°=720°;
…
同理:∠A1+∠A2+∠A3+…+∠A11=10×180°=1800°;
∠A1+∠A2+∠A3+…+∠An+1=180n°;
(2)①∵AB∥EF∥CD,
∴∠B=∠BEF,
∠C=∠CEF,
∴∠B+∠C=∠BEC;
②过G作GN∥AB,
∵AB∥CD,
∴AB∥GN∥CD,
∴∠B+∠EGN=∠E,∠NGF+∠C=∠F,
∴∠B+∠EGF+∠C=∠E+∠F;
③过F作FP∥AB,过H作HQ∥AB,
∵AB∥CD,
∴AB∥FP∥HQ∥CD,
∴∠B+∠EFP=∠E,∠PFG+∠GHQ=∠G,∠QHM+∠C=∠M,
∴∠B+∠EFG+∠GHM+∠C=∠E+∠G+∠M.
【素养提升】
通过对前几个图形中的位置关系和数量关系的分析,归纳总结出所有图形隐含的一般规律。通过这种由特殊到一般的推理,考查了逻辑推理这一核心素养
确定在两条平行线间利用折线得到角之间的关系时,需要过折线的拐点作已知直线的平行线,利用平行线的传递性和平行线的性质解决问题。
三、易错辨析(把握要点真谛)
辨析点一 应用平行线的性质时忽略前提条件
例16、两条直线被第三条直线所截,若∠1与∠2是同旁内角,且∠1=70°,则( )
A、∠2=70° B、∠2=110° C、∠2=70°或∠2=110° D、∠2的度数无法确定
【易错分析】两直线被第三条直线所截,只有当两条被截直线平行时,内错角相等,同位角相等,同旁内角互补.不平行时以上结论不成立。 故选:D
辨析点二 混淆平行线的性质与直线平行的条件
例17、如图,A、B、C和D、E、F分别在同一条直线上,且∠1=∠2,∠C=∠D,试完成下面证明∠A=∠F的过程.
【证明】:∵∠1=∠2(已知),∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换),
∴BD∥CE(同位角相等,两直线平行),
∴∠D+∠DEC=180°(两直线平行,同旁内角互补),
又∵∠C=∠D(已知),
∴∠C+∠DEC=180°(等量代换),
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F
【易错分析】混淆平行线的性质与条件,防止的方法是要看得到什么样的结论,若要得到角的数量关系有要用平行线的性质;若要得到两直线平行,则用两直线平行的条件。
辨析点三 考虑问题不全面,分类讨论运用不熟练
例18、如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.则∠AEC的度数可能是多少?
【解答】(1)如图1,由AB∥CD
可得∠AOC=∠DCE1=β
∵∠AOC=∠BAE1+∠AE1C
∴∠AE1C=β-α.
(2)如图2,过E2作AB平行线,
∵AB∥CD
∴∠1=∠BAE2=α ∠2=∠DCE2=β
∴∠AE2C=α+β.
如图3,∵AB∥CD,
∴∠BOE3=∠DCE3=β
∵∠BAE3=∠BOE3+∠AE3C
∴∠AE3C=α-β.
(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β.
(5)(6)当点E在CD的下方时,同理可得,∠AEC=α-β或β-α.
综上所述,∠AEC的度数可能为β-α,α+β,α-β,360°-α-β.
【易错分析】点E有5种可能位置,因此必须分情况进行讨论。
四、链接中考(直通中考真题)
链接一 平行线的性质
(2020 南通)如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A、36° B、34° C、32° D、30°
【分析】(方法一)过点E作EF∥AB,则EF∥CD,由EF∥AB,利用“两直线平行,内错角相等”可得出∠AEF的度数,结合∠CEF=∠AEF-∠AEC可得出∠CEF的度数,由EF∥CD,利用“两直线平行,内错角相等”可求出∠C的度数;
(方法二)设AE与CD交于点O,由AB∥CD,利用“两直线平行,同位角相等”可得出∠DOE的度数,再利用三角形外角的性质,即可求出∠C的度数
【解答】解:(方法一)过点E作EF∥AB,则EF∥CD,
如图1所示.
∵EF∥AB,
∴∠AEF=∠A=54°,
∵∠CEF=∠AEF-∠AEC=54°-18°=36°.
又∵EF∥CD,
∴∠C=∠CEF=36°.
(方法二)设AE与CD交于点O,如图2所示.
∵AB∥CD,
∴∠DOE=∠A=54°.
又∵∠DOE=∠C+∠E,
∴∠C=∠DOE-∠E=54°-18°=36°.
故选:A
链接二 平行线的性质与直线平行的条件的综合
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A、65° B、66° C、55° D、75°
【解答】解:∵∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠5=180°-∠3=55°,
∴∠4=55°
故选:C
【小结】本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型
符号
语言
文字
叙述
素养指导:平行线性质的规律猜想题
一、探究学习 (问题导引探究)
探究 平行线的性质
素养探究:如果两条直线平行,那么同位角、内错角、同旁内角各有什么关系?
知识导引:
平等线的性质
直线平行与性质之间的关系
例1 【基础题】 如图,AB∥CD,∠ADC=∠ABC.求证:∠E=∠F
【分析】平行 角相等 (等量代换)角相等
平行线的性质是由“性质关系”得到“数量关系”,直线平行的条件是由“数量关系”得到“位置关系”。直接利用平行线的性质得出∠ABC=∠DCF,再利用已知得出∠E=∠F.
【证明】∵AB∥CD,
∴∠ABC=∠DCF.
又∵∠ADC=∠ABC
∴∠ADC=∠DCF.
∴DE∥BF.
∴∠E=∠F.
小结:此题主要考查了平行线的判定与性质,正确得出∠ADC=∠DCF是解题关键.
例2 【基础题】
【分析】 三个小题都是已知两线段平行和∠1的度数,求∠2的度数。在应用两直线平行的条件和平行线的性质时,一般使用同位角、内错角相等和同旁内角互补,如果已知不是的时候,可以借助对顶角等特殊角的性质将其转化为上述三种类型的角。
二、解题指导 (思路决定成败)
类型一、利用平行线的性质进行角的度数计算
例3 【中难题】如图,直线a∥b,直线AB与直线a,b分别相交于点A、B,AC交直线b于点C.(1)若AC⊥AB,∠1=54°49′.求∠2的度数;2)请说明∠ABC+∠BCA+∠CAB=180°.
【分析】(1)依据直线a∥b,AC⊥AB,即可得到∠2=90°-∠3=35°11′;
(2)利用平行线的性质定理可得结论。
【解答】(1)如图,
∵直线a∥b,
∴∠3=∠1=54°49′,
又∵AC⊥AB,
∴∠2=90°-∠3=35°11′;
(2)∵a∥b,
∴∠ACB=∠3,
∠ABC=∠4,
∵∠4+∠3+∠BAC=180°,
∴∠ABC+∠BCA+∠CAB=180°.
小结:本题主要考查平行线的性质了平行线的性质定理,解题的关键是掌握:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.解题过程还需准确掌握度分秒的换算和垂线的定义。
例4【中难题】如图,AB∥CD,EF⊥AB于O,∠FGD=140°,求∠EFG的度数.
【分析】过点F作FM∥AB,则FM∥CD,利用“两直线平行,同旁内角互补”可求出∠MFG的度数,由EF⊥AB可得出∠BOF=90°,结合FM∥AB可求出∠OFM的度数,再利用∠EFG=∠OFM+∠MFG即可求出∠EFG的度数.
【解答】过点F作FM∥AB,如图所示.
∵AB∥CD,FM∥AB,
∴FM∥CD,
∴∠MFG=180°-∠FGD=180°-140°=40°.
∵EF⊥AB,
∴∠BOF=90°,
又∵FM∥AB,
∴∠OFM=180°-∠BOF=180°-90°=90°,
∴∠EFG=∠OFM+∠MFG=90°+40°=130°.
小结:本题考查了平行线的性质以及垂线,牢记“两直线平行,同旁内角互补”是解题关键
例5【中难题】 如图把一个含有30°角的直角三角板的直角顶点A放在直线a上,a∥b,B、C两点在平面上移动,请根据如下条件解答:
(1)如图1,若点C在直线b上,点B在直线b的下方,∠2=20°,则∠1=40°;
(2)如图2,若点C在平行直线a,b内部,点B在直线b的下方,∠2=n°,求∠1度数.
【分析】由含有30°的直角三角板可知∠ACB=60°.
(1)根据平行线的性质可得∠1=∠3,由∠2+∠3=∠ACB=60°,∠2=20°,可求解∠1的度数;
(2)过点C作直线c∥a,根据平行线的性质可得∠1=∠4,再判定c∥b,可得∠2=∠5,由∠ACB=60°,可求解∠1+∠2=60°,利用∠2=n°,即可求出∠1的度数
【解答】由题意可知:∠BAC=90°,∠B=30°,则∠ACB=60°.
(1)如图1,∵a∥b,
∴∠1=∠3,
∵∠2+∠3=∠ACB=60°, ∠2=20°,
∴∠3=40°,
(2)如图2,过C作c∥a,
∴∠1=∠4,
∵a∥b,
∴c∥b,
∴∠2=∠5,
∵∠4+∠5=∠ACB=60°,
∴∠1+∠2=60°,
∵∠2=n°,
∴∠1=(60-n)°.
【小结】本题主要考查平行线的性质与判定,三角形的内角和定理,要能从直角三角板求解∠ACB=60°,关注此类题辅助线的画法
例6【中难题】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2-∠1=16°
【分析】先利用平行线的性质得∠2=∠DEG,∠EFG=∠DEF=49°,再根据折叠的性质得∠DEF=∠GEF=49°,所以∠2=98°,接着利用互补计算出∠1,然后计算∠2-∠1
【解答】∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°-98°=82°,
∴∠2-∠1=98°-82°=16°
【小结】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质
类型二、利用平行线的性质探究角的关系
例7【中难题】如图,已知AB∥CD,AE∥CF,求证:∠BAE=∠DCF
【分析】根据两直线平行,内错角相等的性质以及角的和差关系可证明
【证明】:∵AB∥CD,
∴∠BAC=∠DCA.(两直线平行,内错角相等)
∵AE∥CF,
∴∠EAC=∠FCA.(两直线平行,内错角相等)
∵∠BAC=∠BAE+∠EAC,∠DCA=∠DCF+∠FCA,
∴∠BAE=∠DCF
小结:重点考查了两直线平行,内错角相等的这一性质
例8【中难题】如图,AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC平分∠ABP交AM于点C,BD平分∠PBN交AM于点D.
(1)求∠ABN的度数.
(2)求∠CBD的度数.
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若变化,请写出变化规律;若不变化,请写出它们之间的数量关系,并说明理由.
【分析】(1)由AM∥BN,利用“两直线平行,同旁内角互补”可求出∠ABN的度数;
(2)由BC平分∠ABP,BD平分∠PBN,利用角平分线的定义可得出∠CBP=∠ABP,∠PBD=∠PBN,再结合∠CBD=∠CBP+∠PBD即可求出∠CBD的度数;
(3)由AM∥BN,利用“两直线平行,内错角相等”可得出 ∠APB=∠PBN,∠ADB=∠DBN,结合角平分线的定义可得出∠APB=2∠ADB.
【解答】(1)∵AM∥BN,
∴∠A+∠ABN=180°,
∴∠ABN=180°-∠A=180°-60°=120°.
(2)∵BC平分∠ABP,BD平分∠PBN,
∴∠CBP=∠ABP,∠PBD=∠PBN
∴∠CBD=∠CBP+∠PBD=∠ABP+∠PBN=∠ABN=60°.
(3)不变,∠APB=2∠ADB,理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PDN, ∴∠PBN=2∠DBN,
∴∠APB=2∠ADB.
小结:本题考查了平行线的性质以及角平分线的定义,解题的关键是:(1)牢记“两直线平行,同旁内角互补”;(2)利用角平分线的定义,找出∠CBP=∠ABP,∠PBD=
∠PBN;(3)牢记“两直线平行,内错角相等”.
类型三、利用平行线的性质解决实际问题
例9【基础题】 如图,某人骑自行车自A沿正东方向前进,至B处后,行使方向改为东偏南15°,行驶到C处仍按正东方向行驶,画出继续行驶的路线
【分析】对于生活中的问题,要能够抽象出相应的几何图形,并转化成数学问题,然后利用所学两直线平行,同旁内角互补的知识来解决,以C为顶点作165°的角即可
【小结】本题主要考查了两直线平行,同旁内角互补的性质.
例10【中难题】如图,是我们生活中经常接触的小刀,由刀片和刀柄组成,在刀柄ABCD中,∠A和∠B都是直角,在刀片EFGH中,EF∥GH.转动刀片时会形成∠1、∠2,试判断∠1与∠2的度数和是一个定值吗?若是,请求出∠1与∠2的度数和;若不是,请说明理由
【分析】过点B作BP∥EF,则∠1=∠ABP.依据平行线的性质,即可得到∠ABP+∠PBC=∠1+∠2=90°
【解答】∠1与∠2的度数和是一个定值,∠1+∠2=90°
如图,过点B作BP∥EF,则∠1=∠ABP.
∵EF∥GH,
∴BP∥GH,
∴∠2=∠PBC,
∵∠ABP+∠PBC=90°,
∴∠1+∠2=90°
类型四、利用平行线的性质与直线平行的条件综合运用
例11【中难题】
如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理
【分析】由题意可先猜测∠AED=∠C,那么需证明DE∥BC.题中说∠1+∠2=180°,而∠1+∠4=180°所以∠2=∠4,那么可得到BD∥EF,题中有∠3=∠B,所以应根据平行得到∠3与∠ADE之间的关系为相等.就得到∠B与∠ADE之间的关系为相等,那么DE∥BC
【解答】∠AED=∠C.
证明:∵∠1+∠4=180°(邻补角定义)
∠1+∠2=180°(已知)
∴∠2=∠4(同角的补角相等)
∴EF∥AB(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
又∵∠B=∠3(已知),
∴∠ADE=∠B(等量代换),
∴DE∥BC(同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等).
小结:本题是先从结论出发得到需证明的条件,又从所给条件入手,得到需证明的条件.属于典型的从两头往中间证明
例12【中难题】如图,已知AD⊥BC,EF⊥BC,垂足分别是D、F.∠1=∠2,∠3=100°,试求∠BAC的度数
【分析】根据平行线的判定与性质可求得∠CGD=80°,∠B=∠GDC,再结合三角形的内角和定理可求解∠BAC的度数
【解答】∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,∠1+∠B=90°,∠2+∠GDC=90°,
∵∠1=∠2,∠3=100°,
∴∠CGD=80°,∠B=∠GDC,
∵∠DGC+∠C+∠GDC=180°,
∴∠B+∠C=100°,
∵∠BAC+∠B+∠C=180°,
∴∠BAC=180°-(∠B+∠C)=180°-100°=80°,
故∠BAC的度数为80°
小结:本题主要考查三角形的内角和定理,垂线的定义,平行线的性质等知识的综合运用
【综合法与分析法】几何推理的方法主要有两种:一种是综合法,即由“因”导“果”,由已知条件逐步推到出结论,;另一种是分析法,即执“果”索“因”,根据要推出的结论,找到所需的条件,一步一步倒推,逐渐靠近已知条件。解答时一般用综合法,分析问题市一般用分析法,有时也可以综合应用两种方法。
类型五、分类讨论
例13【基础题】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.
解:如图:
(1)∠APC=∠PAB+∠PCD;
证明:过点P作PF∥AB,则AB∥CD∥PF,
∴∠APC=∠PAB+∠PCD(两直线平行,内错角相等).
(2)∠APC+∠PAB+∠PCD=360°;
(3)∠APC=∠PAB-∠PCD;
(4)∵AB∥CD,
∴∠POB=∠PCD,
∵∠POB是△AOP的外角,
∴∠APC+∠PAB=∠POB,
∴∠APC=∠POB-∠PAB,
∴∠APC=∠PCD-∠PAB
【分析—辅助线法】两条平行线之间存在拐点时,通常过拐点作平行线,构造出同位角、内错角、同旁内角,为应用平行线的性质创造条件。
例14【拓展题】已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.
(1)如图1,过点E作EH∥AB,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(2)如图2,类比(1)中的方法,运用上述结论,探究∠PEQ、∠APE、∠CQE之间的数量关系,并说明理由;
(3)如图3,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,直接写出∠PFQ度数.
【分析】从拐点作出平行线(1)证出AB∥EH∥CD,由平行线的性质∠APE=∠PEH,∠CQE=∠QEH.进而得出结论;
(2)证出AB∥EG∥CD,由平行线的性质得∠APE+∠PEG=180°,∠CQE+∠QEG=180°,进而得出结论;
(3)由(2)得∠PEQ+∠BPE+∠EQD=360°,求出∠BPE+∠EQD=220°,由角平分线定义得∠BPF+∠DQF=∠BPE+∠EQD)=110°,由(1)得∠PFQ=∠BPF+∠DQF=110°
解:(1)∠PEQ=∠APE+∠CQE,理由如下:
∵AB∥CD,EH∥AB,
∴AB∥EH∥CD,
∴∠APE=∠PEH,∠CQE=∠QEH.
∵∠PEQ=∠PEH+∠QEH,
∴∠PEQ=∠APE+∠CQE.
(2)∠APE+∠CQE+∠PEQ=360°;理由如下:
过点E作EG∥AB,如图2所示:
∵AB∥CD,EG∥AB,
∴AB∥EG∥CD,
∴∠APE+∠PEG=180°,∠CQE+∠QEG=180°,
∴∠APE+∠PEG+∠CQE+∠QEG=360°,
即∠APE+∠CQE+∠PEQ=360°;
小结:在拐点作已知平行线的平行线就本节常见题型,掌握技巧,才能更好解决问题。
细观察,找规律.
例15 、下列各图中的MA1与NAn平行.
①图①中的∠A1+∠A2=180度.
②图②中的∠A1+∠A2+∠A3=360度.
③图③中的∠A1+∠A2+∠A3+∠A4=540度.
④图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720度.
⑤第⑩个图中的∠A1+∠A2+∠A3+…+∠A11=1800度.
⑥第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n度.
下列各图中AB∥CD.
①图甲中∠B、∠C、∠BEC的数量关系是∠B+∠C=∠BEC.
②图乙中∠B,∠E,∠G,∠F,∠C的数量关系是∠B+∠EGF+∠C=∠E+∠F.
③图丙中∠B,∠E,∠F,∠G,∠H,∠M,∠C的数量关系是
∠B+∠EFG+∠GHM+∠C=∠E+∠G+∠M.
【分析】(1)通过作平行线,由平行线的性质可逐题求解,注意找规律;
【解答】解:(1)∵MA1∥NA2, ∴∠A1+∠A2=180°;
过A2作A2P∥MA1,
∵MA1∥NA3, ∴A2P∥NA3,
∴∠A1+∠A2+∠A3=2×180°=360°;
过A2作A2P∥MA1,过A3作A3Q∥MA1,
∵MA1∥NA4, ∴A2P∥MA1∥A3Q∥NA4,
∴∠A1+∠A2+∠A3+∠A4=3×180°=540°;
过A2作A2P∥MA1,过A3作A3Q∥MA1,过A4作A4B∥MA1,
∵MA1∥NA5, ∴A2P∥MA1∥A3Q∥A4B∥NA5,
∴∠A1+∠A2+∠A3+∠A4+∠A5=4×180°=720°;
…
同理:∠A1+∠A2+∠A3+…+∠A11=10×180°=1800°;
∠A1+∠A2+∠A3+…+∠An+1=180n°;
(2)①∵AB∥EF∥CD,
∴∠B=∠BEF,
∠C=∠CEF,
∴∠B+∠C=∠BEC;
②过G作GN∥AB,
∵AB∥CD,
∴AB∥GN∥CD,
∴∠B+∠EGN=∠E,∠NGF+∠C=∠F,
∴∠B+∠EGF+∠C=∠E+∠F;
③过F作FP∥AB,过H作HQ∥AB,
∵AB∥CD,
∴AB∥FP∥HQ∥CD,
∴∠B+∠EFP=∠E,∠PFG+∠GHQ=∠G,∠QHM+∠C=∠M,
∴∠B+∠EFG+∠GHM+∠C=∠E+∠G+∠M.
【素养提升】
通过对前几个图形中的位置关系和数量关系的分析,归纳总结出所有图形隐含的一般规律。通过这种由特殊到一般的推理,考查了逻辑推理这一核心素养
确定在两条平行线间利用折线得到角之间的关系时,需要过折线的拐点作已知直线的平行线,利用平行线的传递性和平行线的性质解决问题。
三、易错辨析(把握要点真谛)
辨析点一 应用平行线的性质时忽略前提条件
例16、两条直线被第三条直线所截,若∠1与∠2是同旁内角,且∠1=70°,则( )
A、∠2=70° B、∠2=110° C、∠2=70°或∠2=110° D、∠2的度数无法确定
【易错分析】两直线被第三条直线所截,只有当两条被截直线平行时,内错角相等,同位角相等,同旁内角互补.不平行时以上结论不成立。 故选:D
辨析点二 混淆平行线的性质与直线平行的条件
例17、如图,A、B、C和D、E、F分别在同一条直线上,且∠1=∠2,∠C=∠D,试完成下面证明∠A=∠F的过程.
【证明】:∵∠1=∠2(已知),∠2=∠3(对顶角相等)
∴∠1=∠3(等量代换),
∴BD∥CE(同位角相等,两直线平行),
∴∠D+∠DEC=180°(两直线平行,同旁内角互补),
又∵∠C=∠D(已知),
∴∠C+∠DEC=180°(等量代换),
∴DF∥AC(同旁内角互补,两直线平行),
∴∠A=∠F
【易错分析】混淆平行线的性质与条件,防止的方法是要看得到什么样的结论,若要得到角的数量关系有要用平行线的性质;若要得到两直线平行,则用两直线平行的条件。
辨析点三 考虑问题不全面,分类讨论运用不熟练
例18、如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.则∠AEC的度数可能是多少?
【解答】(1)如图1,由AB∥CD
可得∠AOC=∠DCE1=β
∵∠AOC=∠BAE1+∠AE1C
∴∠AE1C=β-α.
(2)如图2,过E2作AB平行线,
∵AB∥CD
∴∠1=∠BAE2=α ∠2=∠DCE2=β
∴∠AE2C=α+β.
如图3,∵AB∥CD,
∴∠BOE3=∠DCE3=β
∵∠BAE3=∠BOE3+∠AE3C
∴∠AE3C=α-β.
(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β.
(5)(6)当点E在CD的下方时,同理可得,∠AEC=α-β或β-α.
综上所述,∠AEC的度数可能为β-α,α+β,α-β,360°-α-β.
【易错分析】点E有5种可能位置,因此必须分情况进行讨论。
四、链接中考(直通中考真题)
链接一 平行线的性质
(2020 南通)如图,已知AB∥CD,∠A=54°,∠E=18°,则∠C的度数是( )
A、36° B、34° C、32° D、30°
【分析】(方法一)过点E作EF∥AB,则EF∥CD,由EF∥AB,利用“两直线平行,内错角相等”可得出∠AEF的度数,结合∠CEF=∠AEF-∠AEC可得出∠CEF的度数,由EF∥CD,利用“两直线平行,内错角相等”可求出∠C的度数;
(方法二)设AE与CD交于点O,由AB∥CD,利用“两直线平行,同位角相等”可得出∠DOE的度数,再利用三角形外角的性质,即可求出∠C的度数
【解答】解:(方法一)过点E作EF∥AB,则EF∥CD,
如图1所示.
∵EF∥AB,
∴∠AEF=∠A=54°,
∵∠CEF=∠AEF-∠AEC=54°-18°=36°.
又∵EF∥CD,
∴∠C=∠CEF=36°.
(方法二)设AE与CD交于点O,如图2所示.
∵AB∥CD,
∴∠DOE=∠A=54°.
又∵∠DOE=∠C+∠E,
∴∠C=∠DOE-∠E=54°-18°=36°.
故选:A
链接二 平行线的性质与直线平行的条件的综合
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是( )
A、65° B、66° C、55° D、75°
【解答】解:∵∠1=∠2,
∴a∥b,
∴∠4=∠5,
∵∠5=180°-∠3=55°,
∴∠4=55°
故选:C
【小结】本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型
符号
语言
文字
叙述
素养指导:平行线性质的规律猜想题
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
