2021-2022学年华东师大版七年级数学上册第5章相交线与平行线 期末复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版七年级数学上册第5章相交线与平行线 期末复习训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 168.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 10:17:33 | ||
图片预览

文档简介
2021-2022学年华师大版七年级数学上册《第5章相交线与平行线》期末复习训练(附答案)
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3 B.0、1或3 C.0、1或2 D.0、1、2或3
2.如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
3.如图,直线AB、CD、EF相交于O点,则图中小于平角的对顶角有( )对.
A.3 B.5 C.6 D.8
4.如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
5.在同一平面内有直线a1,a2,a3,a4,…,a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,按此规律进行下去,则a1与a100的位置关系是( )
A.平行 B.相交 C.重合 D.无法判断
6.下列说法正确的是( )
A.一个角的补角一定大于这个角
B.若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余
C.点到直线之间,垂线段最短
D.相等的角是对顶角
7.下列说法正确的有( )
①不相交的两条直线是平行线;
②同旁内角相等,两直线平行;
③若线段AB与CD没有交点,则AB∥CD;
④a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
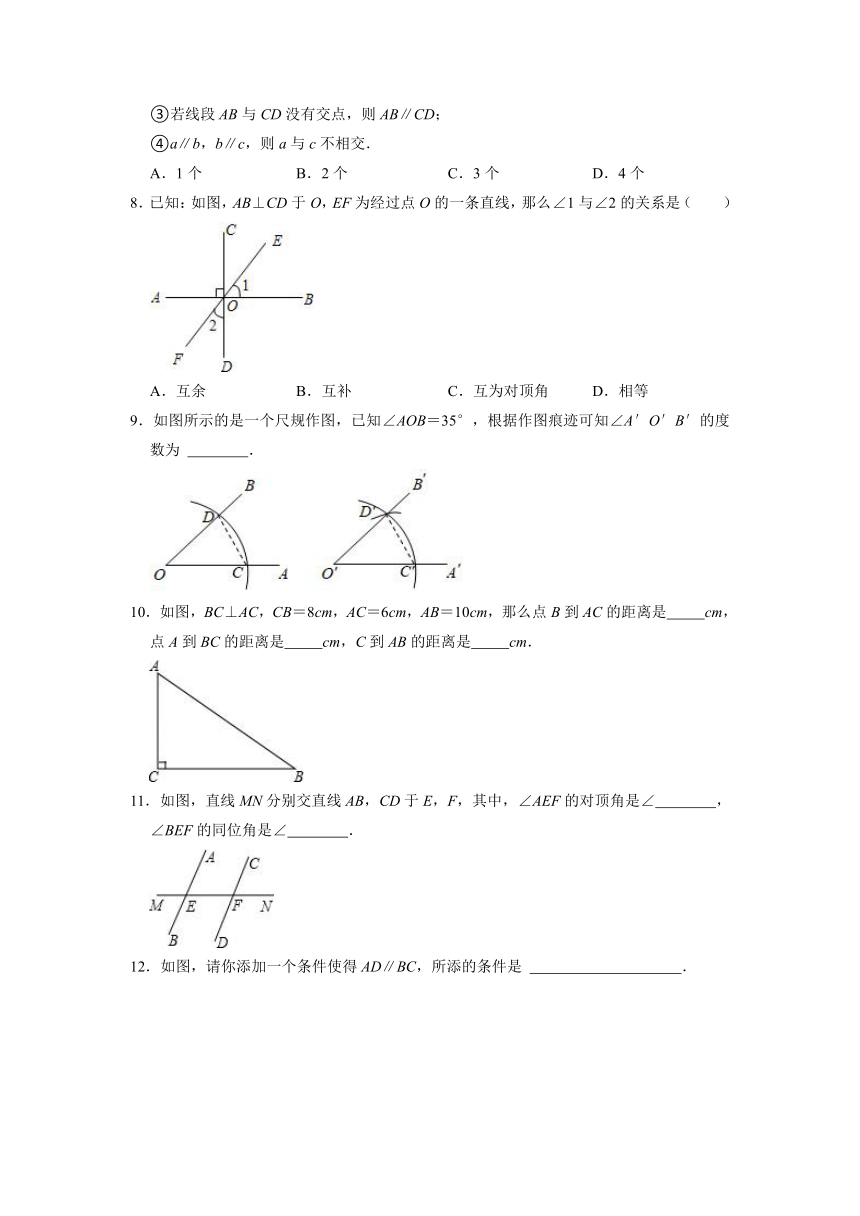
8.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互余 B.互补 C.互为对顶角 D.相等
9.如图所示的是一个尺规作图,已知∠AOB=35°,根据作图痕迹可知∠A′O′B′的度数为 .
10.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是 cm,点A到BC的距离是 cm,C到AB的距离是 cm.
11.如图,直线MN分别交直线AB,CD于E,F,其中,∠AEF的对顶角是∠ ,∠BEF的同位角是∠ .
12.如图,请你添加一个条件使得AD∥BC,所添的条件是 .
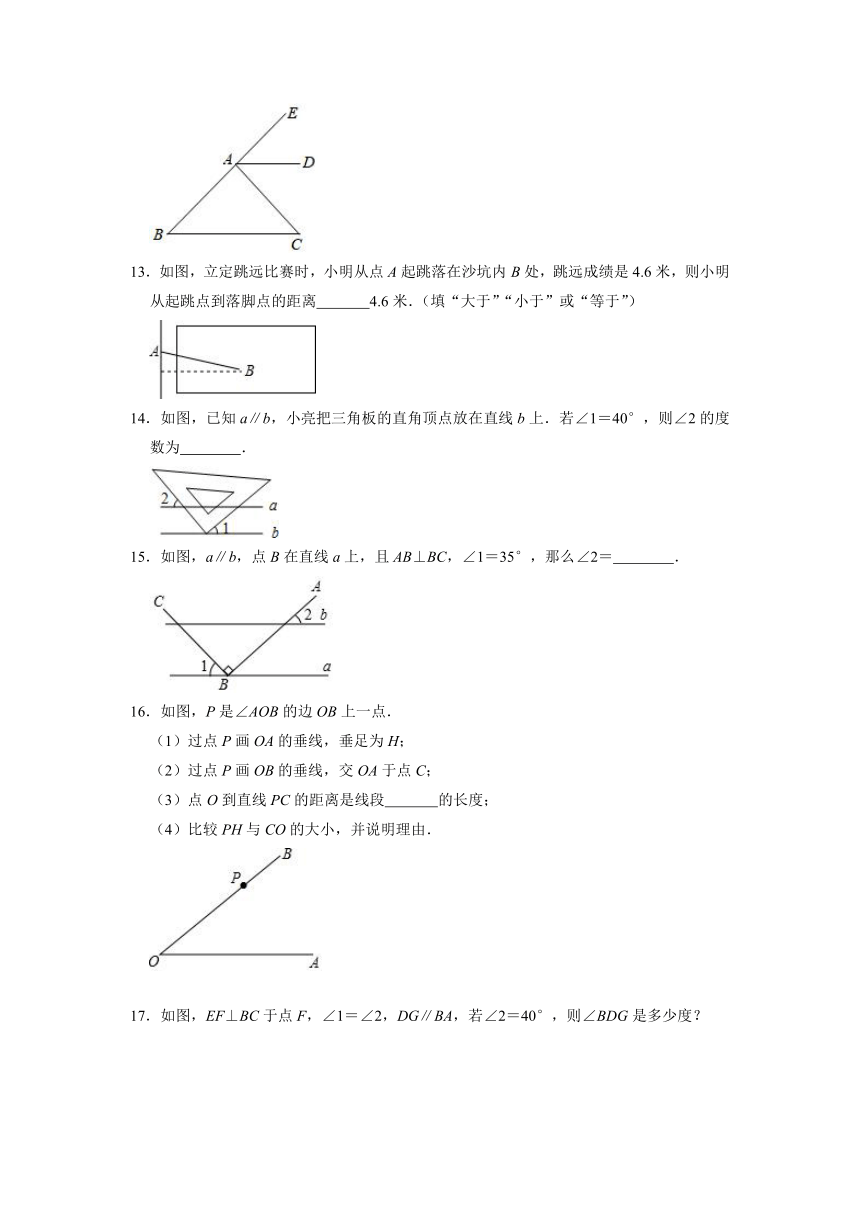
13.如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米.(填“大于”“小于”或“等于”)
14.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为 .
15.如图,a∥b,点B在直线a上,且AB⊥BC,∠1=35°,那么∠2= .
16.如图,P是∠AOB的边OB上一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)点O到直线PC的距离是线段 的长度;
(4)比较PH与CO的大小,并说明理由.
17.如图,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
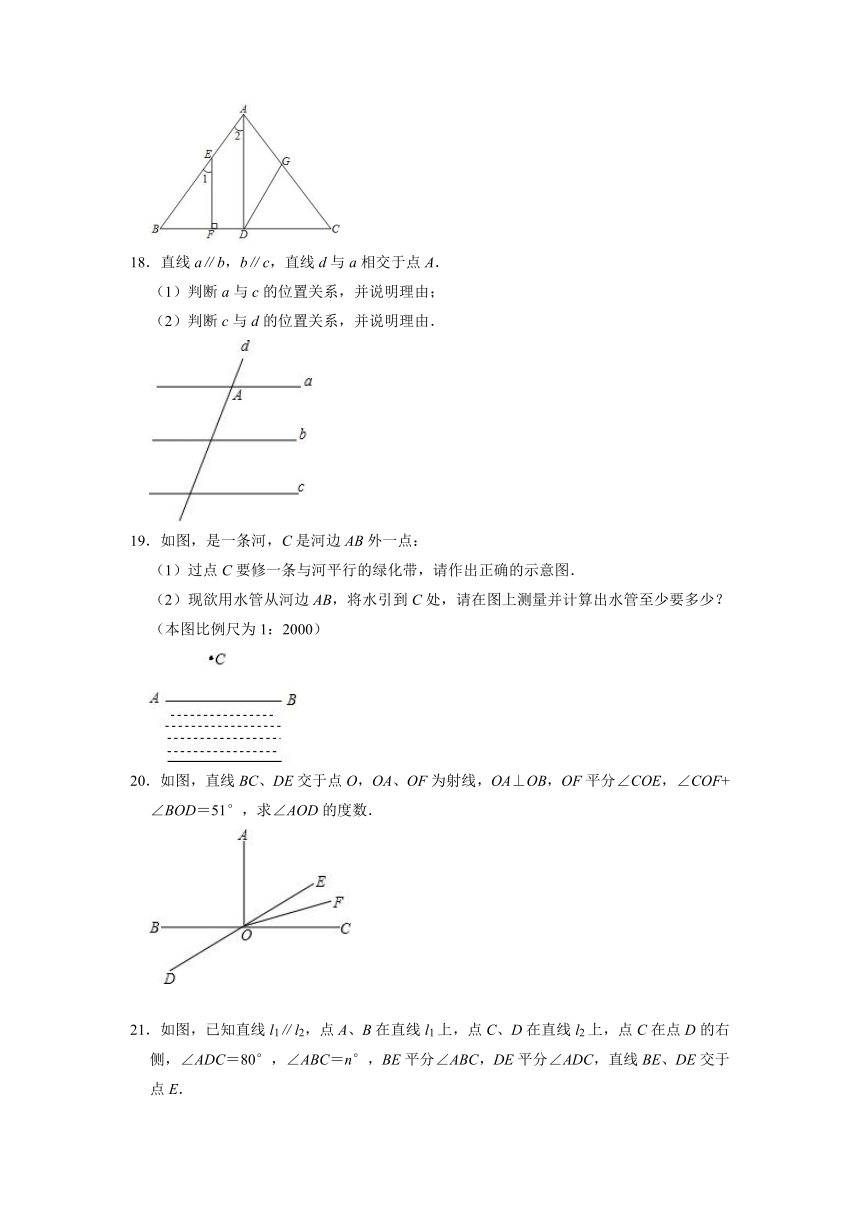
18.直线a∥b,b∥c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;
(2)判断c与d的位置关系,并说明理由.
19.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
20.如图,直线BC、DE交于点O,OA、OF为射线,OA⊥OB,OF平分∠COE,∠COF+∠BOD=51°,求∠AOD的度数.
21.如图,已知直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,点C在点D的右侧,∠ADC=80°,∠ABC=n°,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
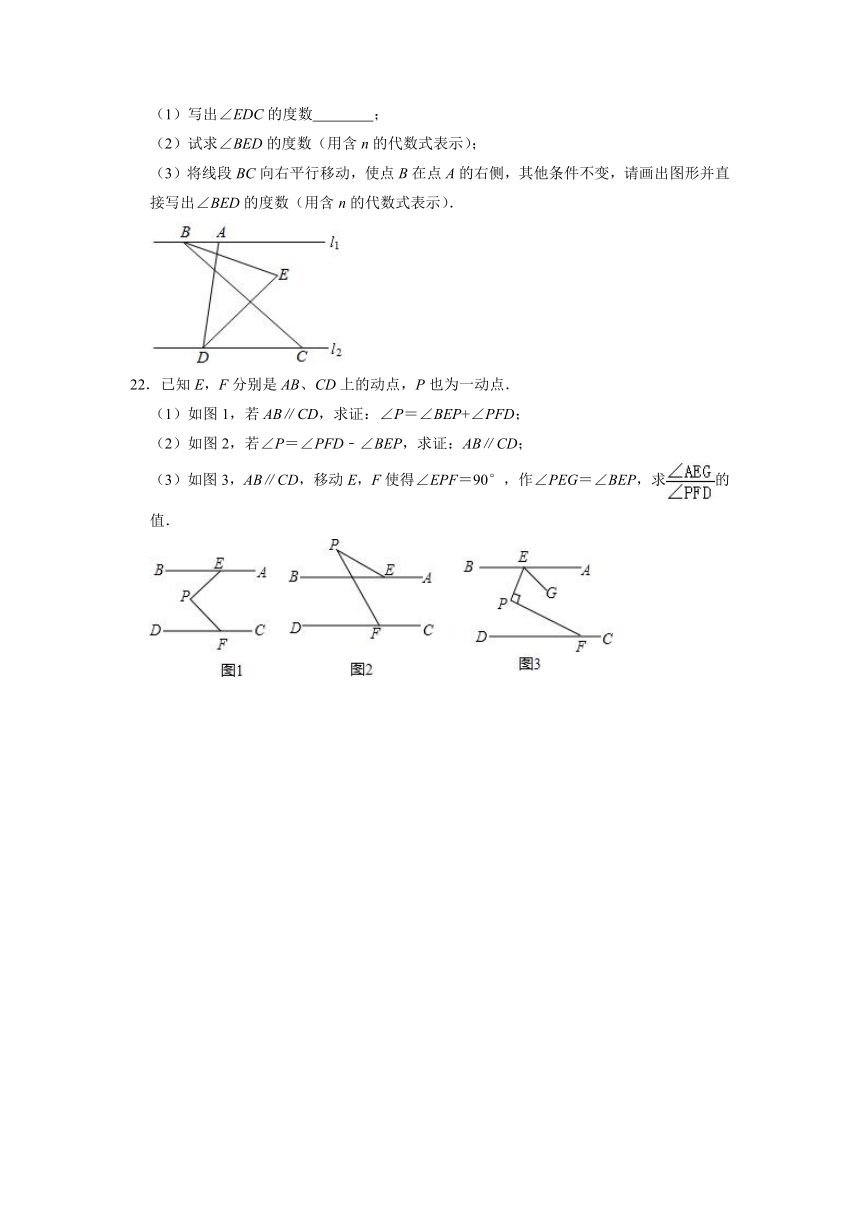
(1)写出∠EDC的度数 ;
(2)试求∠BED的度数(用含n的代数式表示);
(3)将线段BC向右平行移动,使点B在点A的右侧,其他条件不变,请画出图形并直接写出∠BED的度数(用含n的代数式表示).
22.已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.
参考答案
1.解:如图,三条直线的交点个数可能是0或1或2或3.
故选:D.
2.解:如图,,
根据点到直线的距离的含义,可得
点C到直线AB的距离是线段CD的长.
故选:B.
3.解:图中对顶角有:∠AOF与∠BOE、∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
故选:C.
4.解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠BOC+∠AOD=90°﹣∠AOB+90°+∠AOB=180°,故②正确;
∠AOB+∠COD不一定等于90°,故③错误;
图中小于平角的角有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD一共6个,故④正确;
综上所述,说法正确的是①②④.
故选:C.
5.解:由a1⊥a2,a2∥a3,得a1⊥a3,
由a3⊥a4,得a1∥a4.
由此类推:a1⊥a6,a1∥a8
每4条出现重复:与前面的垂直,后面的平行.
∴a1∥a100,
故选:A.
6.解:A、一个角的补角不一定大于这个角,故错误,不符合题意;
B、互余是两个锐角之间的关系,故错误,不符合题意;
C、点到直线之间,垂线段最短,正确,符合题意;
D、相等的角不一定是对顶角,故错误,不符合题意,
故选:C.
7.解:①在同一平面内,不相交的两条直线是平行线,故说法错误;
②同旁内角互补,两直线平行,故说法错误;
③若线段AB与CD没有交点,但不能判定AB∥CD,故说法错误;
④a∥b,b∥c,则a与c不相交,故说法正确;
故选:A.
8.解:∵AB⊥CD,
∴∠BOD=90°.
又∵EF为过点O的一条直线,
∴∠1+∠2=180°﹣∠BOD=90°,即∠1与∠2互余.
故选:A.
9.解:用作图可知,∠A′O′B′=∠AOB=35°,
故答案为:35°.
10.解:如图,过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,
∵BC⊥AC,CB=8cm,AB=10cm,AC=6cm,
∴CD=6×8÷2×2÷10=4.8cm,
点A到BC的距离是6cm,
点B到AC的距离是8cm.
故答案为:8,6、4.8.
11.解:∠AEF的对顶角是∠BEM,∠BEF的同位角是∠DFN.
12.解:根据同位角相等,两条直线平行,可以添加∠EAD=∠B;
根据内错角相等,两条直线平行,可以添加∠CAD=∠C;
根据同旁内角互补,两条直线平行,可以添加∠BAD+∠B=180°,
故答案为:∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180°.
13.解:∵根据跳远成绩为距离起跳线最近的点到起跳线的距离,即垂线段的长,
又∵垂线段最短,
∴小明从起跳点到落脚点之间的距离大于4.6米,
故答案为:大于.
14.解:∵∠1=40°,
∴∠3=180°﹣∠1﹣90°=180°﹣40°﹣90°=50°,
∵a∥b,
∴∠2=∠3=50°.
故答案为:50°.
15.解:∵a∥b,∠1=35°,
∴∠3=∠1=35°.
∵AB⊥BC,
∴∠2=90°﹣∠3=55°.
故答案为:55°.
16.解:(1)作图,
(2)作图,
(3)OP,
故答案为:OP;
(4)PH<CO,
∵垂线段最短,
∴PH<PO,PO<OC,
∴PH<CO.
17.解:∵∠1=∠2,
∴EF∥AD,
∵EF⊥BC,
∴AD⊥BC,即∠ADB=90°,
又∵DG∥BA,∠2=40°,
∴∠ADG=∠2=40°,
∴∠BDG=∠ADG+∠ADB=130°.
18.解:(1)a与c的位置关系是平行,
理由是:∵直线a∥b,b∥c,
∴a∥c;
(2)c与d的位置关系是相交,
理由是:∵c∥a,直线d与a相交于点A,
∴c与d的位置关系是相交.
19.解:如图:
(1)过点C画一平行线平行于AB.
(2)过点C作CD垂直于AB交AB于点D.
然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.
20.解:设∠COF=x,
∵OF平分∠COE,
∴∠COE=2∠COF=2x,
∴∠BOD=∠COE=2x(对顶角相等),
∵∠COF+∠BOD=51°,
∴x+2x=51°,
解得x=17°,
∴∠BOD=2×17°=34°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
21.解:(1)∵DE平分∠ADC,∠ADC=80°,
∴∠EDC=∠ADC=×80°=40°;
故答案为:40°;
(2)如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∴∠BED=∠BEF+∠DEF=n°+40°;
(3)过点E作EF∥AB,
如图,点A在点B的左边时,
若点E在直线l1和l2之间,则
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEF=40°,
∴∠BED=∠BEF+∠DEF=180°﹣n°+40°=220°﹣n°.
综上所述,∠BED的度数变化,度数为220°﹣n°.
22.解:(1)过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD;
(2)∵∠BGP是△PEG的外角,
∴∠P=∠BGP﹣∠BEP.
∵∠P=∠PGB﹣∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD;
(3)由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°﹣x,
∵∠PEG=∠BEP=90°﹣x,
∴∠AEG=180°﹣2(90°﹣x)=2x,则==2
1.同一平面内,三条不同直线的交点个数可能是( )个.
A.1或3 B.0、1或3 C.0、1或2 D.0、1、2或3
2.如图,△ABC是锐角三角形,过点C作CD⊥AB,垂足为D,则点C到直线AB的距离是( )
A.线段CA的长 B.线段CD的长 C.线段AD的长 D.线段AB的长
3.如图,直线AB、CD、EF相交于O点,则图中小于平角的对顶角有( )对.
A.3 B.5 C.6 D.8
4.如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
A.1个 B.2个 C.3个 D.4个
5.在同一平面内有直线a1,a2,a3,a4,…,a100,若a1⊥a2,a2∥a3,a3⊥a4,a4∥a5,…,按此规律进行下去,则a1与a100的位置关系是( )
A.平行 B.相交 C.重合 D.无法判断
6.下列说法正确的是( )
A.一个角的补角一定大于这个角
B.若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余
C.点到直线之间,垂线段最短
D.相等的角是对顶角
7.下列说法正确的有( )
①不相交的两条直线是平行线;
②同旁内角相等,两直线平行;
③若线段AB与CD没有交点,则AB∥CD;
④a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
8.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互余 B.互补 C.互为对顶角 D.相等
9.如图所示的是一个尺规作图,已知∠AOB=35°,根据作图痕迹可知∠A′O′B′的度数为 .
10.如图,BC⊥AC,CB=8cm,AC=6cm,AB=10cm,那么点B到AC的距离是 cm,点A到BC的距离是 cm,C到AB的距离是 cm.
11.如图,直线MN分别交直线AB,CD于E,F,其中,∠AEF的对顶角是∠ ,∠BEF的同位角是∠ .
12.如图,请你添加一个条件使得AD∥BC,所添的条件是 .
13.如图,立定跳远比赛时,小明从点A起跳落在沙坑内B处,跳远成绩是4.6米,则小明从起跳点到落脚点的距离 4.6米.(填“大于”“小于”或“等于”)
14.如图,已知a∥b,小亮把三角板的直角顶点放在直线b上.若∠1=40°,则∠2的度数为 .
15.如图,a∥b,点B在直线a上,且AB⊥BC,∠1=35°,那么∠2= .
16.如图,P是∠AOB的边OB上一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)点O到直线PC的距离是线段 的长度;
(4)比较PH与CO的大小,并说明理由.
17.如图,EF⊥BC于点F,∠1=∠2,DG∥BA,若∠2=40°,则∠BDG是多少度?
18.直线a∥b,b∥c,直线d与a相交于点A.
(1)判断a与c的位置关系,并说明理由;
(2)判断c与d的位置关系,并说明理由.
19.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
20.如图,直线BC、DE交于点O,OA、OF为射线,OA⊥OB,OF平分∠COE,∠COF+∠BOD=51°,求∠AOD的度数.
21.如图,已知直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,点C在点D的右侧,∠ADC=80°,∠ABC=n°,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
(1)写出∠EDC的度数 ;
(2)试求∠BED的度数(用含n的代数式表示);
(3)将线段BC向右平行移动,使点B在点A的右侧,其他条件不变,请画出图形并直接写出∠BED的度数(用含n的代数式表示).
22.已知E,F分别是AB、CD上的动点,P也为一动点.
(1)如图1,若AB∥CD,求证:∠P=∠BEP+∠PFD;
(2)如图2,若∠P=∠PFD﹣∠BEP,求证:AB∥CD;
(3)如图3,AB∥CD,移动E,F使得∠EPF=90°,作∠PEG=∠BEP,求的值.
参考答案
1.解:如图,三条直线的交点个数可能是0或1或2或3.
故选:D.
2.解:如图,,
根据点到直线的距离的含义,可得
点C到直线AB的距离是线段CD的长.
故选:B.
3.解:图中对顶角有:∠AOF与∠BOE、∠AOD与∠BOC、∠FOD与∠EOC、∠FOB与∠AOE、∠DOB与∠AOC、∠DOE与∠COF,共6对.
故选:C.
4.解:∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠COD+∠BOC=90°,
∴∠AOB=∠COD,故①正确;
∠BOC+∠AOD=90°﹣∠AOB+90°+∠AOB=180°,故②正确;
∠AOB+∠COD不一定等于90°,故③错误;
图中小于平角的角有∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠COD一共6个,故④正确;
综上所述,说法正确的是①②④.
故选:C.
5.解:由a1⊥a2,a2∥a3,得a1⊥a3,
由a3⊥a4,得a1∥a4.
由此类推:a1⊥a6,a1∥a8
每4条出现重复:与前面的垂直,后面的平行.
∴a1∥a100,
故选:A.
6.解:A、一个角的补角不一定大于这个角,故错误,不符合题意;
B、互余是两个锐角之间的关系,故错误,不符合题意;
C、点到直线之间,垂线段最短,正确,符合题意;
D、相等的角不一定是对顶角,故错误,不符合题意,
故选:C.
7.解:①在同一平面内,不相交的两条直线是平行线,故说法错误;
②同旁内角互补,两直线平行,故说法错误;
③若线段AB与CD没有交点,但不能判定AB∥CD,故说法错误;
④a∥b,b∥c,则a与c不相交,故说法正确;
故选:A.
8.解:∵AB⊥CD,
∴∠BOD=90°.
又∵EF为过点O的一条直线,
∴∠1+∠2=180°﹣∠BOD=90°,即∠1与∠2互余.
故选:A.
9.解:用作图可知,∠A′O′B′=∠AOB=35°,
故答案为:35°.
10.解:如图,过点C作CD⊥AB于点D,则线段CD的长即为点C到AB的距离,
∵BC⊥AC,CB=8cm,AB=10cm,AC=6cm,
∴CD=6×8÷2×2÷10=4.8cm,
点A到BC的距离是6cm,
点B到AC的距离是8cm.
故答案为:8,6、4.8.
11.解:∠AEF的对顶角是∠BEM,∠BEF的同位角是∠DFN.
12.解:根据同位角相等,两条直线平行,可以添加∠EAD=∠B;
根据内错角相等,两条直线平行,可以添加∠CAD=∠C;
根据同旁内角互补,两条直线平行,可以添加∠BAD+∠B=180°,
故答案为:∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180°.
13.解:∵根据跳远成绩为距离起跳线最近的点到起跳线的距离,即垂线段的长,
又∵垂线段最短,
∴小明从起跳点到落脚点之间的距离大于4.6米,
故答案为:大于.
14.解:∵∠1=40°,
∴∠3=180°﹣∠1﹣90°=180°﹣40°﹣90°=50°,
∵a∥b,
∴∠2=∠3=50°.
故答案为:50°.
15.解:∵a∥b,∠1=35°,
∴∠3=∠1=35°.
∵AB⊥BC,
∴∠2=90°﹣∠3=55°.
故答案为:55°.
16.解:(1)作图,
(2)作图,
(3)OP,
故答案为:OP;
(4)PH<CO,
∵垂线段最短,
∴PH<PO,PO<OC,
∴PH<CO.
17.解:∵∠1=∠2,
∴EF∥AD,
∵EF⊥BC,
∴AD⊥BC,即∠ADB=90°,
又∵DG∥BA,∠2=40°,
∴∠ADG=∠2=40°,
∴∠BDG=∠ADG+∠ADB=130°.
18.解:(1)a与c的位置关系是平行,
理由是:∵直线a∥b,b∥c,
∴a∥c;
(2)c与d的位置关系是相交,
理由是:∵c∥a,直线d与a相交于点A,
∴c与d的位置关系是相交.
19.解:如图:
(1)过点C画一平行线平行于AB.
(2)过点C作CD垂直于AB交AB于点D.
然后用尺子量CD的长度,再按1:2000的比例求得实际距离即可.
20.解:设∠COF=x,
∵OF平分∠COE,
∴∠COE=2∠COF=2x,
∴∠BOD=∠COE=2x(对顶角相等),
∵∠COF+∠BOD=51°,
∴x+2x=51°,
解得x=17°,
∴∠BOD=2×17°=34°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
21.解:(1)∵DE平分∠ADC,∠ADC=80°,
∴∠EDC=∠ADC=×80°=40°;
故答案为:40°;
(2)如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∴∠BED=∠BEF+∠DEF=n°+40°;
(3)过点E作EF∥AB,
如图,点A在点B的左边时,
若点E在直线l1和l2之间,则
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°﹣∠ABE=180°﹣n°,∠CDE=∠DEF=40°,
∴∠BED=∠BEF+∠DEF=180°﹣n°+40°=220°﹣n°.
综上所述,∠BED的度数变化,度数为220°﹣n°.
22.解:(1)过P作PQ∥AB,
∵AB∥CD,
∴PQ∥CD,
∴∠BEP=∠1,∠2=∠PFD,
∵∠EPF=∠1+∠2,
∴∠EPF=∠BEP+∠PFD;
(2)∵∠BGP是△PEG的外角,
∴∠P=∠BGP﹣∠BEP.
∵∠P=∠PGB﹣∠BEP,
∴∠PFD=∠PGB,
∴AB∥CD;
(3)由(1)的结论∠EPF=∠BEP+∠PFD=90°,
设∠PFD=x,则∠BEP=90°﹣x,
∵∠PEG=∠BEP=90°﹣x,
∴∠AEG=180°﹣2(90°﹣x)=2x,则==2
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
