人教版数学七年级下册 5.1.3同位角_内错角_同旁内角 课件(共38张ppt)
文档属性
| 名称 | 人教版数学七年级下册 5.1.3同位角_内错角_同旁内角 课件(共38张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览





文档简介
(共38张PPT)
3
B
A
C
D
O
1
2
4
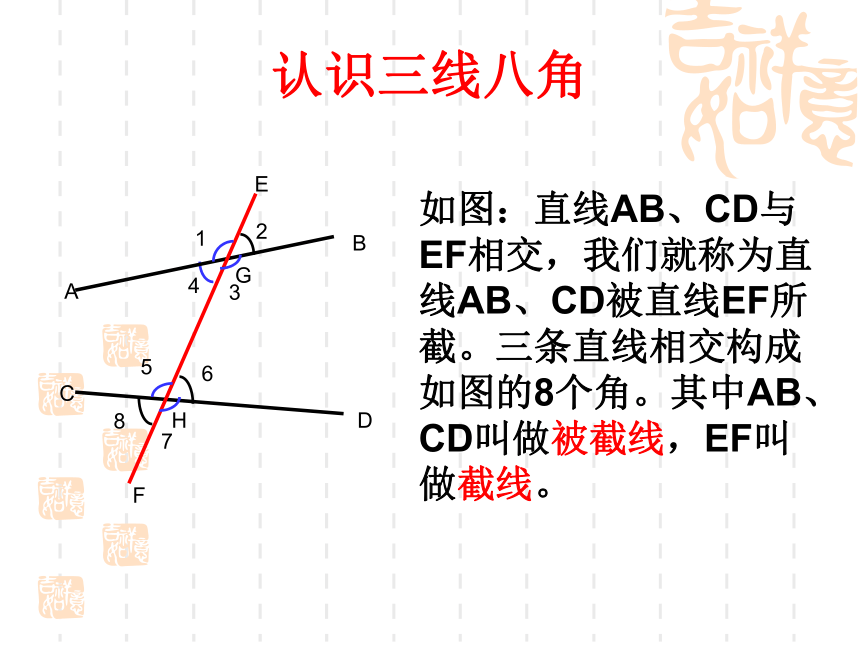
复习:
如图:直线AB与CD相交于点O,请找出图中特殊的角。
对顶角: ∠1与∠3, ∠2与∠4
邻补角:∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4
教学目标:
观察“三线八角”中角的特殊位置关系,归纳同位角,内错角,同旁内角的定义。
根据定义会从图形中识别同位角,内错角,同旁内角。
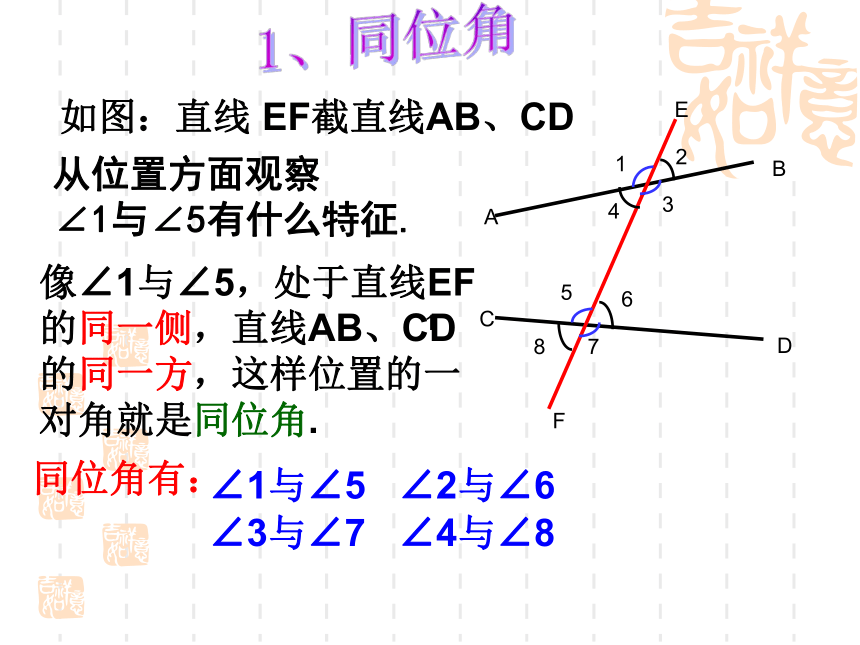
认识三线八角
如图:直线AB、CD与EF相交,我们就称为直线AB、CD被直线EF所截。三条直线相交构成如图的8个角。其中AB、CD叫做被截线,EF叫做截线。
3
C
A
F
E
D
B
H
G
1
2
4
5
6
7
8
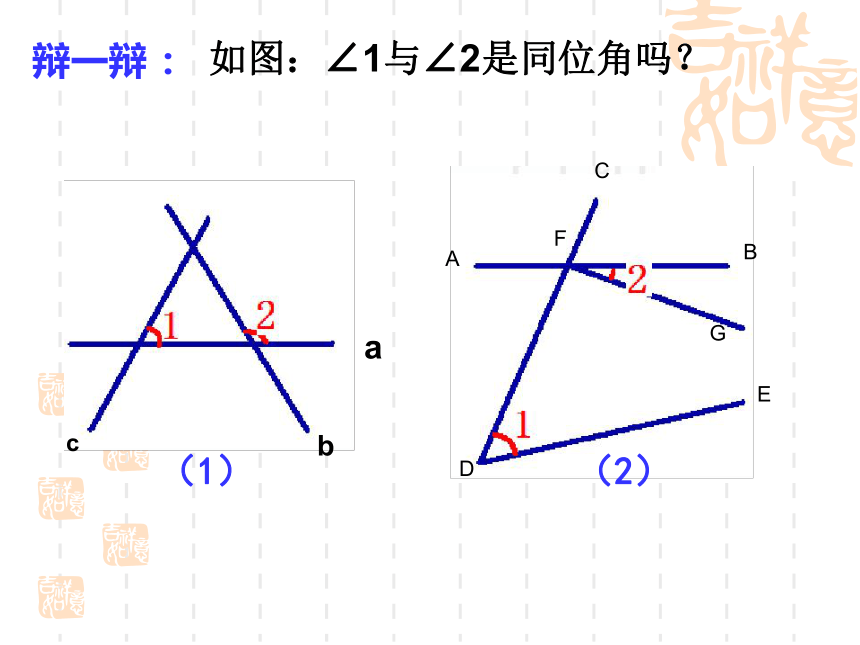
如图:直线 EF截直线AB、CD
像∠1与∠5,处于直线EF的同一侧,直线AB、CD的同一方,这样位置的一对角就是同位角.
同位角有:
∠2与∠6
∠4与∠8
∠3与∠7
从位置方面观察
∠1与∠5有什么特征.
∠1与∠5
C
A
F
E
D
B
1
2
4
5
6
8
1
3
7
辩一辩 :
如图:∠1与∠2是同位角吗?
(1)
(2)
a
b
c
A
C
E
D
B
F
G
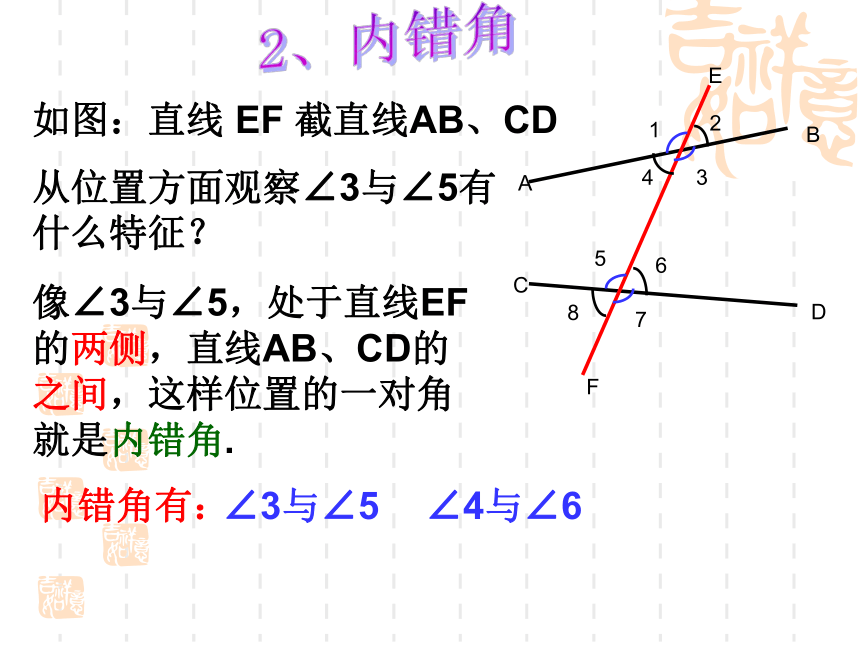
如图:直线 EF 截直线AB、CD
从位置方面观察∠3与∠5有什么特征?
内错角有:
∠4与∠6
像∠3与∠5,处于直线EF的两侧,直线AB、CD的之间,这样位置的一对角就是内错角.
∠3与∠5
C
A
F
E
D
B
1
2
4
5
6
8
3
7
如图:∠1与∠2是内错角吗?
(1)
(2)
a
b
c
A
C
E
D
F
G
B
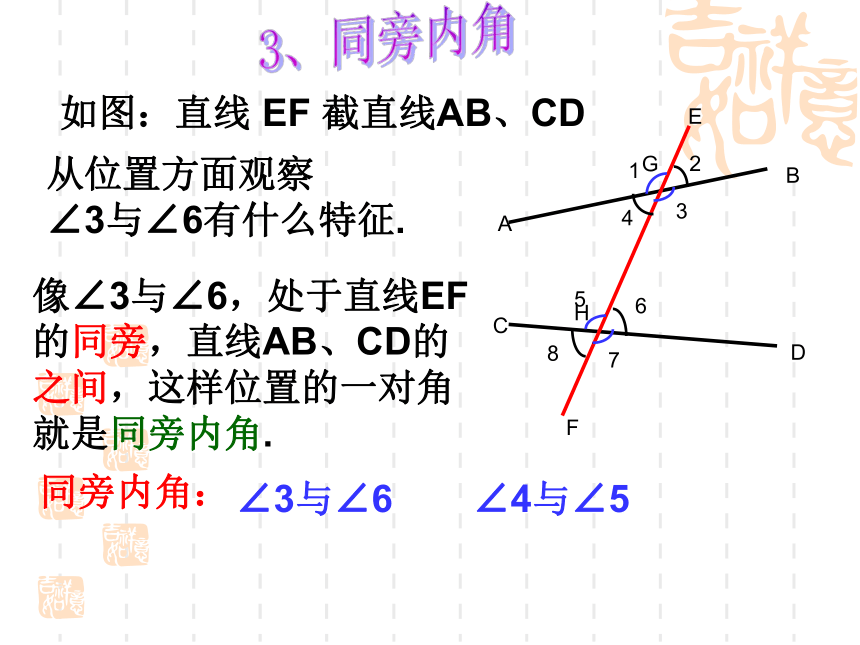
如图:直线 EF 截直线AB、CD
从位置方面观察
∠3与∠6有什么特征.
同旁内角:
∠3与∠6
∠4与∠5
像∠3与∠6,处于直线EF的同旁,直线AB、CD的之间,这样位置的一对角就是同旁内角.
C
A
F
E
D
B
1
2
4
5
6
8
3
7
G
H
如图:∠1与∠2是同旁内角吗?
(1)
(2)
A
C
E
D
F
B
G
b
c
a
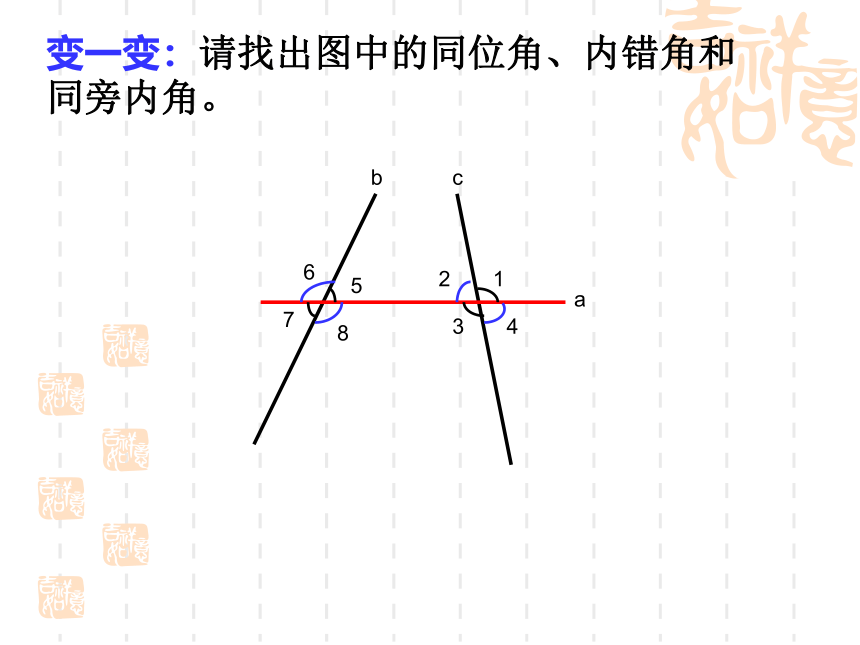
变一变:请找出图中的同位角、内错角和同旁内角。
1
2
3
4
5
6
7
8
a
b
c
同位
同旁内
内错
a
b
c
a
c
c
b
a
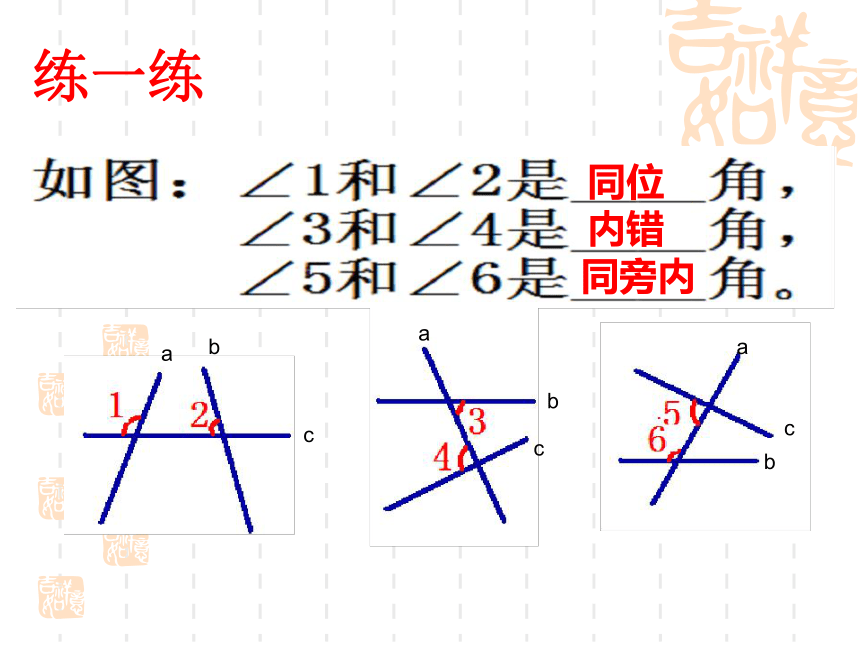
练一练
b
做一做: 如图,直线DE,BC被直线AB所截,
∠1与∠2是___角,∠1与∠3是_ __角,
∠1与∠4是___角。
同位
同旁内
内错
试一试:
根据图形按要求填空:
(1)∠1与∠2是直线
和 被直线 所截而得的 .
AB
DE
BC
同位角
(2) ∠1与∠3是直线 和 被直线 所截而得的 .
AB
DE
BC
内错角
(3)∠3与∠4是
直线 和 被直线 所截而得的 .
BC
EF
DE
内错角
(4)∠2与∠4是
直线 和 被直线 所截而得的 .
BC
EF
DE
同位角
(5)∠4与∠5是
直线 和 被直线 所截而得的 .
BC
EF
DE
同旁内角
归纳:公共边就是“截线”
练一练
根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线 所截而得的 .
(2) ∠3与∠4是直线 和 被直线 所截而得的 .
1
2
3
4
A
B
C
D
E
AB
EC
BD
同位角
AB
EC
AC
内错角
同位角、内错角和同旁内角的结构特征:
∠4与∠8是____角
同位
∠3与∠5是____角
内错
∠4与∠5是____角
同旁内
能力挑战: 看图填空
(2) ∠1与∠2是___与___被____所截形成 的_____角
ED
BF
AB
同位角
能力挑战: 看图填空
(2) ∠4与∠8是___与___被____所截形成 的_____角
ED
FC
DF
内错角
5
∠2与∠5是___与___被____所截形成 的_____角
AB
AF
BF
同旁内
四、生活联系:
新建路
民
人
路
路
京
北
(1)学校与游乐场是( )路与( )路被( )路所截得到的 角。
(2)与学校位置是内错角关系的是( )
A、游乐场 B、书店 C、超市
(3)学校与书店的位置是什么角关系?
交通指南
游乐场
学
学校
超市
书店
北京
人民
新 建
同位
C
它们的位置是同旁内角
如图,∠1与∠B、∠3与∠4、∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么关系的角?
B
D
E
C
A
1
2
3
4
小结
一.同位角、内错角、同旁内角产生的条件:两条直线被第三条直线所截而成(简称“三线八角”)。
二.找同位角、内错角、同旁内角的方法:
(1)先找出截线;
(2)同位角位于截线的同一侧,被截线的同一方。
(3)内错角位于截线的两旁,被截线内部。
(4)同旁内角位于截线的同旁,被截线内部。
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
小结与评价
主要内容:两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
注意:
1、三种角产生的条件及位置特征;
2、判断时应先找到“截线” (“截线”就是两个角的公共边),再找另外两直线,然后根据角的位置决定是哪一种角.
3、当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
(4)∠1与∠B, ∠2与∠3,∠2与∠4分别是什么关系的角。
拓展
解:∠1与∠B是直线AB和直线AD被直线BD所截而成的同旁内角。
∠2与∠3是直线CA和直线CD被直线AD所截而成的同旁内角。
∠2与∠4是直线BA和直线BC被直线AD所截而成的内错角。
1
2
3
4
B
A
C
D
自我检测
练习:
1)如图一:AC截直线AB和DE得∠1与∠A是 。
A、同位角 B、内错角 C、同旁内角 D、对顶角
2)如图二:下列不正确的是 。
A、∠1与∠3是同位角 B、∠1与∠5是内错角
C、∠1与∠2是同旁内角 D、∠1与∠4是内错角
3)如图三:
1、∠A与∠ACD是直线 和 被直线 所截的 角。
2、优生考虑:∠A与∠ACB是直线 和 被直线
所截的 角。
A
C
D
1
B
1
5
2
4
3
B
D
AB
AC
CD
同旁内
AB
BC
AC
同旁内
图三
图二
图一
A
E
B
1
C
D
A
B
1
如图:
(1)∠1和∠4是直线AB与 被 所 截得的 角。
(2)∠2和∠5是 、 被 所
截得的内错角。
(3)优生考虑:AB、DC被BC所截得的同
旁内角是 。
拓展:
2
A
4
B
C
D
E
5
1
3
CD
BC
同位
CD
BC
AC
∠4与∠BCD
找一找 如图:直线AB、CD被直线EF截的8个角中同位角、内错角、同旁内角。
同位角:
内错角:
同旁内角:
∠1与∠5;∠2与∠6
∠3与∠7;∠4与∠8
∠3与∠5;∠4与∠6
∠4与∠5;∠3与∠6
能力挑战: 看图填空
(1)若ED,BF被AB所截, 则∠1与_____是同位角。
∠2
能力挑战: 看图填空
(2)若ED,BC被AF所截, 则∠3与_____是内错角。
∠4
能力挑战: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
如图,∠1与∠2不能构成同位角的图形是[ ]
D
请同学们完成下列填空:
练习一:
1
2
4
3
6
5
∠1与∠2是 角,
∠3与∠4是 角,
∠5与∠6是 角
同旁内
内错
(F型)
(Z型)
(C型)
同位
3
B
A
C
D
O
1
2
4
复习:
如图:直线AB与CD相交于点O,请找出图中特殊的角。
对顶角: ∠1与∠3, ∠2与∠4
邻补角:∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4
教学目标:
观察“三线八角”中角的特殊位置关系,归纳同位角,内错角,同旁内角的定义。
根据定义会从图形中识别同位角,内错角,同旁内角。
认识三线八角
如图:直线AB、CD与EF相交,我们就称为直线AB、CD被直线EF所截。三条直线相交构成如图的8个角。其中AB、CD叫做被截线,EF叫做截线。
3
C
A
F
E
D
B
H
G
1
2
4
5
6
7
8
如图:直线 EF截直线AB、CD
像∠1与∠5,处于直线EF的同一侧,直线AB、CD的同一方,这样位置的一对角就是同位角.
同位角有:
∠2与∠6
∠4与∠8
∠3与∠7
从位置方面观察
∠1与∠5有什么特征.
∠1与∠5
C
A
F
E
D
B
1
2
4
5
6
8
1
3
7
辩一辩 :
如图:∠1与∠2是同位角吗?
(1)
(2)
a
b
c
A
C
E
D
B
F
G
如图:直线 EF 截直线AB、CD
从位置方面观察∠3与∠5有什么特征?
内错角有:
∠4与∠6
像∠3与∠5,处于直线EF的两侧,直线AB、CD的之间,这样位置的一对角就是内错角.
∠3与∠5
C
A
F
E
D
B
1
2
4
5
6
8
3
7
如图:∠1与∠2是内错角吗?
(1)
(2)
a
b
c
A
C
E
D
F
G
B
如图:直线 EF 截直线AB、CD
从位置方面观察
∠3与∠6有什么特征.
同旁内角:
∠3与∠6
∠4与∠5
像∠3与∠6,处于直线EF的同旁,直线AB、CD的之间,这样位置的一对角就是同旁内角.
C
A
F
E
D
B
1
2
4
5
6
8
3
7
G
H
如图:∠1与∠2是同旁内角吗?
(1)
(2)
A
C
E
D
F
B
G
b
c
a
变一变:请找出图中的同位角、内错角和同旁内角。
1
2
3
4
5
6
7
8
a
b
c
同位
同旁内
内错
a
b
c
a
c
c
b
a
练一练
b
做一做: 如图,直线DE,BC被直线AB所截,
∠1与∠2是___角,∠1与∠3是_ __角,
∠1与∠4是___角。
同位
同旁内
内错
试一试:
根据图形按要求填空:
(1)∠1与∠2是直线
和 被直线 所截而得的 .
AB
DE
BC
同位角
(2) ∠1与∠3是直线 和 被直线 所截而得的 .
AB
DE
BC
内错角
(3)∠3与∠4是
直线 和 被直线 所截而得的 .
BC
EF
DE
内错角
(4)∠2与∠4是
直线 和 被直线 所截而得的 .
BC
EF
DE
同位角
(5)∠4与∠5是
直线 和 被直线 所截而得的 .
BC
EF
DE
同旁内角
归纳:公共边就是“截线”
练一练
根据图形按要求填空:
(1)∠1与∠2是直线 和 被直线 所截而得的 .
(2) ∠3与∠4是直线 和 被直线 所截而得的 .
1
2
3
4
A
B
C
D
E
AB
EC
BD
同位角
AB
EC
AC
内错角
同位角、内错角和同旁内角的结构特征:
∠4与∠8是____角
同位
∠3与∠5是____角
内错
∠4与∠5是____角
同旁内
能力挑战: 看图填空
(2) ∠1与∠2是___与___被____所截形成 的_____角
ED
BF
AB
同位角
能力挑战: 看图填空
(2) ∠4与∠8是___与___被____所截形成 的_____角
ED
FC
DF
内错角
5
∠2与∠5是___与___被____所截形成 的_____角
AB
AF
BF
同旁内
四、生活联系:
新建路
民
人
路
路
京
北
(1)学校与游乐场是( )路与( )路被( )路所截得到的 角。
(2)与学校位置是内错角关系的是( )
A、游乐场 B、书店 C、超市
(3)学校与书店的位置是什么角关系?
交通指南
游乐场
学
学校
超市
书店
北京
人民
新 建
同位
C
它们的位置是同旁内角
如图,∠1与∠B、∠3与∠4、∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么关系的角?
B
D
E
C
A
1
2
3
4
小结
一.同位角、内错角、同旁内角产生的条件:两条直线被第三条直线所截而成(简称“三线八角”)。
二.找同位角、内错角、同旁内角的方法:
(1)先找出截线;
(2)同位角位于截线的同一侧,被截线的同一方。
(3)内错角位于截线的两旁,被截线内部。
(4)同旁内角位于截线的同旁,被截线内部。
截线 被截线 结构特征
同位角
内错角
同旁内角
之间
之间
同侧
同旁
两旁
同旁
F
Z
U
小结与评价
主要内容:两条直线被第三条直线所截而产生的三种角——同位角、内错角、同旁内角.
注意:
1、三种角产生的条件及位置特征;
2、判断时应先找到“截线” (“截线”就是两个角的公共边),再找另外两直线,然后根据角的位置决定是哪一种角.
3、当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
(4)∠1与∠B, ∠2与∠3,∠2与∠4分别是什么关系的角。
拓展
解:∠1与∠B是直线AB和直线AD被直线BD所截而成的同旁内角。
∠2与∠3是直线CA和直线CD被直线AD所截而成的同旁内角。
∠2与∠4是直线BA和直线BC被直线AD所截而成的内错角。
1
2
3
4
B
A
C
D
自我检测
练习:
1)如图一:AC截直线AB和DE得∠1与∠A是 。
A、同位角 B、内错角 C、同旁内角 D、对顶角
2)如图二:下列不正确的是 。
A、∠1与∠3是同位角 B、∠1与∠5是内错角
C、∠1与∠2是同旁内角 D、∠1与∠4是内错角
3)如图三:
1、∠A与∠ACD是直线 和 被直线 所截的 角。
2、优生考虑:∠A与∠ACB是直线 和 被直线
所截的 角。
A
C
D
1
B
1
5
2
4
3
B
D
AB
AC
CD
同旁内
AB
BC
AC
同旁内
图三
图二
图一
A
E
B
1
C
D
A
B
1
如图:
(1)∠1和∠4是直线AB与 被 所 截得的 角。
(2)∠2和∠5是 、 被 所
截得的内错角。
(3)优生考虑:AB、DC被BC所截得的同
旁内角是 。
拓展:
2
A
4
B
C
D
E
5
1
3
CD
BC
同位
CD
BC
AC
∠4与∠BCD
找一找 如图:直线AB、CD被直线EF截的8个角中同位角、内错角、同旁内角。
同位角:
内错角:
同旁内角:
∠1与∠5;∠2与∠6
∠3与∠7;∠4与∠8
∠3与∠5;∠4与∠6
∠4与∠5;∠3与∠6
能力挑战: 看图填空
(1)若ED,BF被AB所截, 则∠1与_____是同位角。
∠2
能力挑战: 看图填空
(2)若ED,BC被AF所截, 则∠3与_____是内错角。
∠4
能力挑战: 看图填空
(3)∠1与∠3是AB和AF被_____所截构成的_______角。
DE
内错
如图,∠1与∠2不能构成同位角的图形是[ ]
D
请同学们完成下列填空:
练习一:
1
2
4
3
6
5
∠1与∠2是 角,
∠3与∠4是 角,
∠5与∠6是 角
同旁内
内错
(F型)
(Z型)
(C型)
同位
