沪科版数学八年级上册 13.2 三角形内角和定理的证明 课件(共17张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 13.2 三角形内角和定理的证明 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 632.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 11:09:25 | ||
图片预览




文档简介
(共17张PPT)
13.2 三角形内角和定理的证明
回顾
我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗
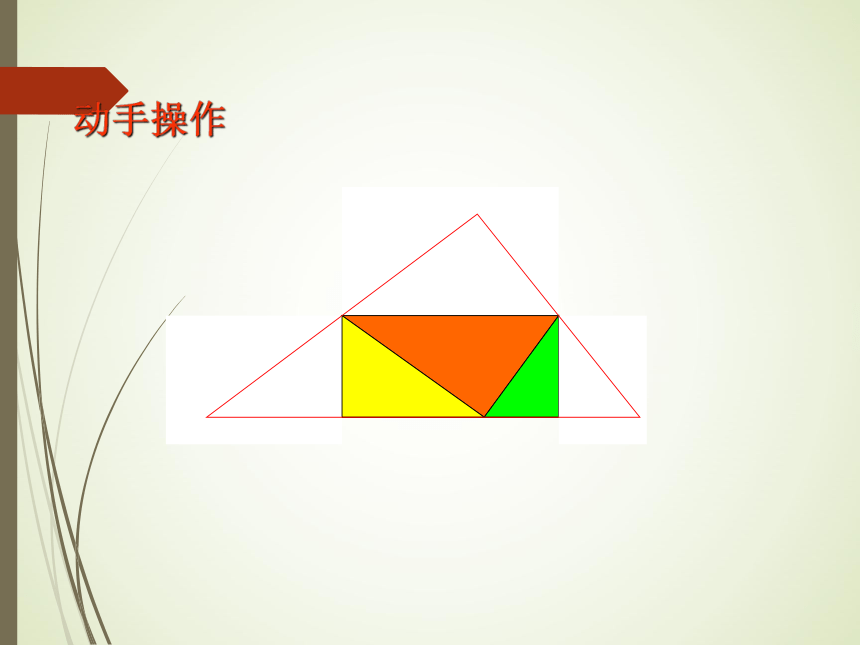
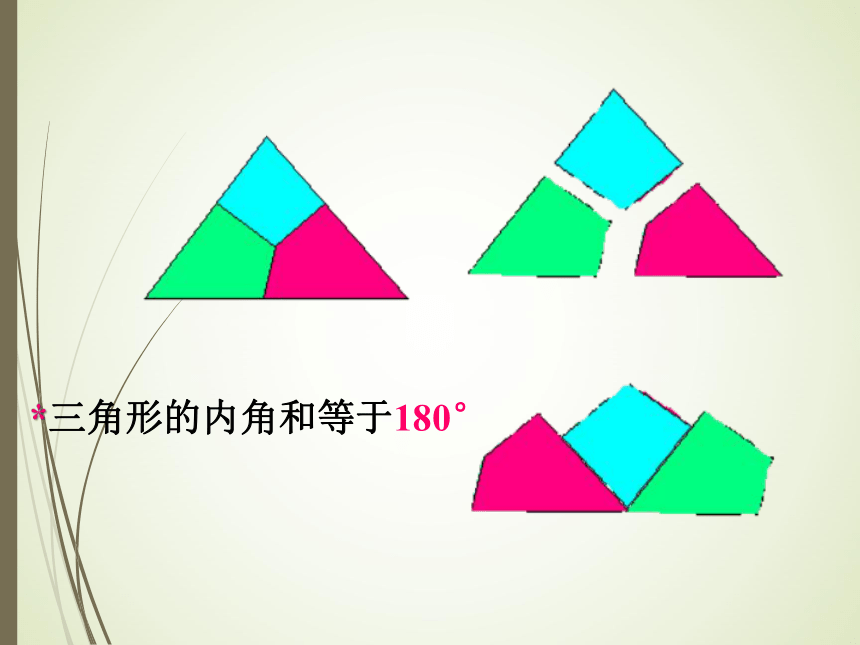
动手操作
*三角形的内角和等于180°
探究:
前面我们通过动手操作使用剪拼、测量等方法得出三角形三个内角和是180度,在操作中我们是把三角形的三个内角拼成一个平角来做的,那么如何用几何证明的方法来证明三角形三个内角和是180度呢?我们是不是也要把三角形的三个角构成一个平角呢?具体怎么做?
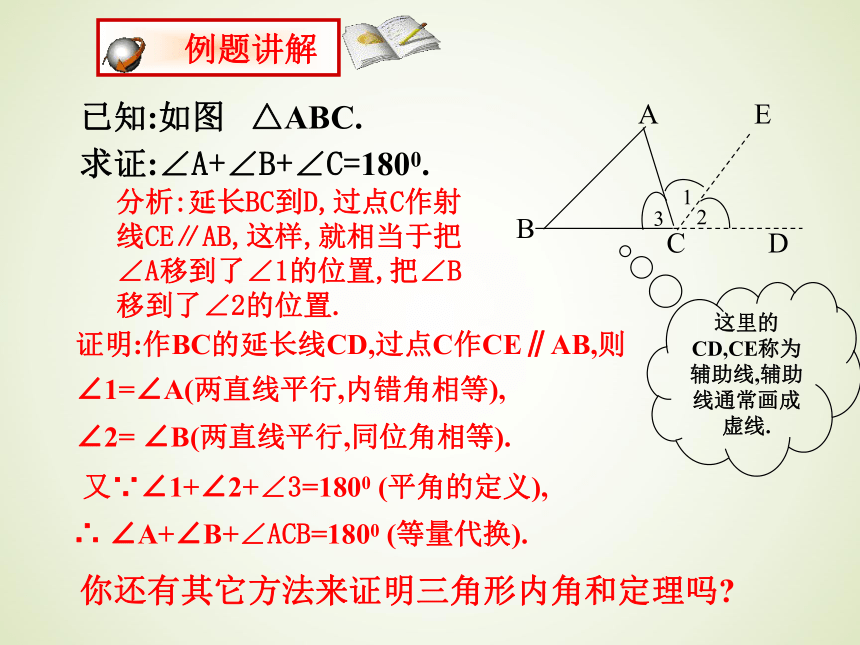
已知:如图 △ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
例题讲解
你还有其它方法来证明三角形内角和定理吗
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
一题多解:
C
B
A
已知:如图,△ABC
求证: ∠ A+∠B+ ∠C=180°.
证明:过A作EF∥BC,
F
2
1
E
C
B
A
∵ EF∥BC(作图)
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°(平角的定义)
∴∠B+∠C+∠BAC=180°
补充完成下列证明
已知:如图,△ABC
求证:∠A+∠B+∠C=1800
A
B
C
D
F
E
证明:D是BC边上的一点,过D点作DE∥AB,DF∥AC,分别交AC,AB于点E,F.
∵ DE∥AB(作图)
你还有其他方法来证明三角形内角和定理吗?
E
A
B
C
D
F
方法总结
添加辅助线思路:构造平角
F
2
1
E
C
B
A
添加辅助线思路:构造同旁内角
A
B
C
E
(
A
B
C
E
D
F
(
(
1
2
3
4
(
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
回顾与思考
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路;
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
猜想直角三角形的两锐角之和是多少度
请证明你的结论.
猜想与思考
推论1: 直角三角形的两个锐角互余.
A
C
B
由基本事实、定理直接得出的真命题叫做推论
推论2: 有两个锐角互余的三角形是直角三角形.
求证:直角三角形的两个锐角互余.
已知:
求证:
学生动手尝试证明推论一
求证:有两个锐角互余的三角形是直角三角形.(推论2)
已知:如图,在△ABC中, ∠A+∠B=900
求证: △ABC是直角三角形
证明: ∵ ∠A+∠B+∠C=1800
∴ ∠C=1800 -(∠A+∠B)
又∵∠A+∠B=900
∴ ∠C=900
故△ABC是直角三角形
本课小结:
谈谈本节课你的收获!
课堂作业:
P84 习题13.2 第6、7、8题
13.2 三角形内角和定理的证明
回顾
我们知道三角形三个内角的和等于1800.你还记得这个结论的探索过程吗
动手操作
*三角形的内角和等于180°
探究:
前面我们通过动手操作使用剪拼、测量等方法得出三角形三个内角和是180度,在操作中我们是把三角形的三个内角拼成一个平角来做的,那么如何用几何证明的方法来证明三角形三个内角和是180度呢?我们是不是也要把三角形的三个角构成一个平角呢?具体怎么做?
已知:如图 △ABC.
求证:∠A+∠B+∠C=1800.
证明:作BC的延长线CD,过点C作CE∥AB,则
例题讲解
你还有其它方法来证明三角形内角和定理吗
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3=1800 (平角的定义),
∴ ∠A+∠B+∠ACB=1800 (等量代换).
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
一题多解:
C
B
A
已知:如图,△ABC
求证: ∠ A+∠B+ ∠C=180°.
证明:过A作EF∥BC,
F
2
1
E
C
B
A
∵ EF∥BC(作图)
∴∠B=∠2(两直线平行,内错角相等)
∠C=∠1(两直线平行,内错角相等)
又 ∵∠2+∠1+∠BAC=180°(平角的定义)
∴∠B+∠C+∠BAC=180°
补充完成下列证明
已知:如图,△ABC
求证:∠A+∠B+∠C=1800
A
B
C
D
F
E
证明:D是BC边上的一点,过D点作DE∥AB,DF∥AC,分别交AC,AB于点E,F.
∵ DE∥AB(作图)
你还有其他方法来证明三角形内角和定理吗?
E
A
B
C
D
F
方法总结
添加辅助线思路:构造平角
F
2
1
E
C
B
A
添加辅助线思路:构造同旁内角
A
B
C
E
(
A
B
C
E
D
F
(
(
1
2
3
4
(
证明命题的一般步骤:
(1)理解题意:分清命题的条件(已知),结论(求证);
回顾与思考
(2)根据题意,画出图形;
(3)结合图形,用符号语言写出“已知”和“求证”;
(4)分析题意,探索证明思路;
(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;
(6)检查表达过程是否正确,完善.
猜想直角三角形的两锐角之和是多少度
请证明你的结论.
猜想与思考
推论1: 直角三角形的两个锐角互余.
A
C
B
由基本事实、定理直接得出的真命题叫做推论
推论2: 有两个锐角互余的三角形是直角三角形.
求证:直角三角形的两个锐角互余.
已知:
求证:
学生动手尝试证明推论一
求证:有两个锐角互余的三角形是直角三角形.(推论2)
已知:如图,在△ABC中, ∠A+∠B=900
求证: △ABC是直角三角形
证明: ∵ ∠A+∠B+∠C=1800
∴ ∠C=1800 -(∠A+∠B)
又∵∠A+∠B=900
∴ ∠C=900
故△ABC是直角三角形
本课小结:
谈谈本节课你的收获!
课堂作业:
P84 习题13.2 第6、7、8题
