沪科版数学八年级上册 11.1 平面内点的坐标(2) 教案
文档属性
| 名称 | 沪科版数学八年级上册 11.1 平面内点的坐标(2) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 31.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览

文档简介
平面上点的坐标(1)
学习目标:
1、认识并掌握直角坐标系的相关知识,能独立地画出平面直角坐标系。
2、通过现实中有序实数对的实例,理解“有序’,使学生掌握有序实数对与点的一一对应必须通过平面直角坐标系这个必要平台。
3、通过本节课的学习,认识平面直角坐标系的作用,激发学生进一步学习的兴趣。
学习重点:认识直角坐标系,理解它是平面内确定点的必要平台。
学习难点:有序实数对的理解
学习过程:
一、知识回顾
1、什么叫数轴?它有哪三要素?实数与数轴有怎样的关系?
2、请你试着画一条数轴,并把下列各数在数轴上表示出来。
3,-4,0.3,,0,-0.3 (表示的点可以近似标出)
二、自主学习
1、(活动)任意说出本班的几位同学的名字,让他说出自己座位的位置。
2、通常数轴上点表示的数叫做这个点的坐标,并把它放在()里。
(1)如下图E(-2) 请分别写出数轴上下列各点的坐标:
A( ) B( ) C( ) D( )
(2)在数轴上分别画出坐标如下的点:
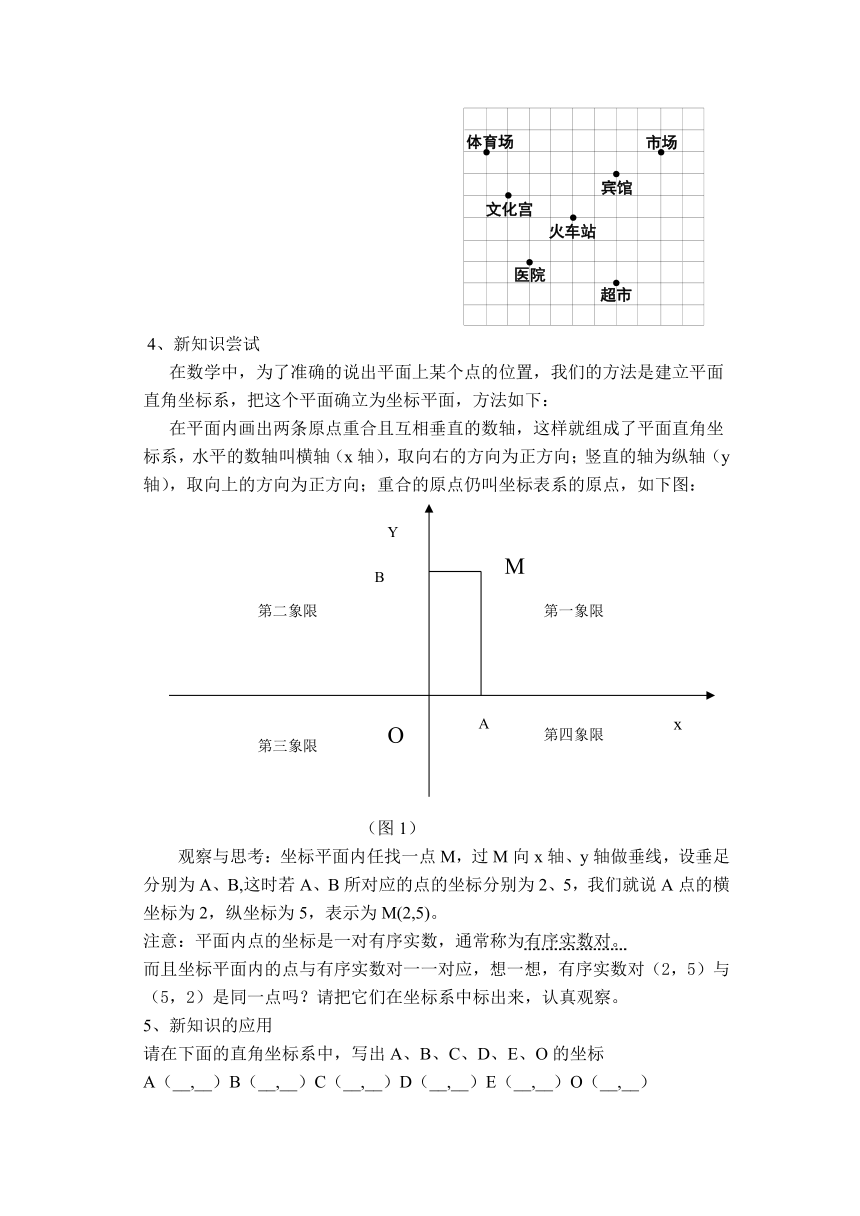
3、如图,这是某市部分简图,小明现在的位置是在火车站,若小明想到图中其他几个地方去,请你用电话准确告诉他,试试看!
4、新知识尝试
在数学中,为了准确的说出平面上某个点的位置,我们的方法是建立平面直角坐标系,把这个平面确立为坐标平面,方法如下:
在平面内画出两条原点重合且互相垂直的数轴,这样就组成了平面直角坐标系,水平的数轴叫横轴(x轴),取向右的方向为正方向;竖直的轴为纵轴(y轴),取向上的方向为正方向;重合的原点仍叫坐标表系的原点,如下图:
(
M
A
O
B
x
Y
第二象限
第一象限
第三象限
第四象限
)
(图1)
观察与思考:坐标平面内任找一点M,过M向x轴、y轴做垂线,设垂足分别为A、B,这时若A、B所对应的点的坐标分别为2、5,我们就说A点的横坐标为2,纵坐标为5,表示为M(2,5)。
注意:平面内点的坐标是一对有序实数,通常称为有序实数对。
而且坐标平面内的点与有序实数对一一对应,想一想,有序实数对(2,5)与
(5,2)是同一点吗?请把它们在坐标系中标出来,认真观察。
5、新知识的应用
请在下面的直角坐标系中,写出A、B、C、D、E、O的坐标
A(__,__)B(__,__)C(__,__)D(__,__)E(__,__)O(__,__)
(图2)
6、概念解析
在坐标平面内,两条互相垂直的坐标轴可以把坐标平面分为四个各部分,如图1,从右上角开始按逆时针方向,分别称为第一象限、第二象限、第三象限、第四象限,这时应注意坐标轴上的点不属于任何象限。现在请根据坐标系中点的坐标的定义,思考一下,各部分点的坐标的特点,如第一象限(+,+)。
试填空:第二象限( , )第三象限( , )第三象限( , )第四象限( , )x轴上( , )y轴上( , )
三、学习小结
同学们,你们本节课学到了哪些知识,请总结一下:
_______________________________________________________________________
___________________________________________________________________
四、达标检测
(一)、选择题(每题3分)
1、下列各点中,在第二象限的点是 ( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2, -3)
2、已知坐标平面内点M(a,b)在第三象限,那么点N(b, -a)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是 ( )
A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)
4、点E(a,b)到x轴的距离是4,到y轴距离是3,则有 ( )
A.a=3, b=4 B.a=±3,b=±4 C.a=4, b=3 D.a=±4,b=±3
(二)解答题
点A(0,-3),点B(0,-4),点C在x轴上,如果△ABC的面积为15,求点C的坐标.(提示:C点在x轴上的位置有两个)
反思:
_______________________________________________________________________
_______________________________________________________________________
______________________________________________________________________。
学习目标:
1、认识并掌握直角坐标系的相关知识,能独立地画出平面直角坐标系。
2、通过现实中有序实数对的实例,理解“有序’,使学生掌握有序实数对与点的一一对应必须通过平面直角坐标系这个必要平台。
3、通过本节课的学习,认识平面直角坐标系的作用,激发学生进一步学习的兴趣。
学习重点:认识直角坐标系,理解它是平面内确定点的必要平台。
学习难点:有序实数对的理解
学习过程:
一、知识回顾
1、什么叫数轴?它有哪三要素?实数与数轴有怎样的关系?
2、请你试着画一条数轴,并把下列各数在数轴上表示出来。
3,-4,0.3,,0,-0.3 (表示的点可以近似标出)
二、自主学习
1、(活动)任意说出本班的几位同学的名字,让他说出自己座位的位置。
2、通常数轴上点表示的数叫做这个点的坐标,并把它放在()里。
(1)如下图E(-2) 请分别写出数轴上下列各点的坐标:
A( ) B( ) C( ) D( )
(2)在数轴上分别画出坐标如下的点:
3、如图,这是某市部分简图,小明现在的位置是在火车站,若小明想到图中其他几个地方去,请你用电话准确告诉他,试试看!
4、新知识尝试
在数学中,为了准确的说出平面上某个点的位置,我们的方法是建立平面直角坐标系,把这个平面确立为坐标平面,方法如下:
在平面内画出两条原点重合且互相垂直的数轴,这样就组成了平面直角坐标系,水平的数轴叫横轴(x轴),取向右的方向为正方向;竖直的轴为纵轴(y轴),取向上的方向为正方向;重合的原点仍叫坐标表系的原点,如下图:
(
M
A
O
B
x
Y
第二象限
第一象限
第三象限
第四象限
)
(图1)
观察与思考:坐标平面内任找一点M,过M向x轴、y轴做垂线,设垂足分别为A、B,这时若A、B所对应的点的坐标分别为2、5,我们就说A点的横坐标为2,纵坐标为5,表示为M(2,5)。
注意:平面内点的坐标是一对有序实数,通常称为有序实数对。
而且坐标平面内的点与有序实数对一一对应,想一想,有序实数对(2,5)与
(5,2)是同一点吗?请把它们在坐标系中标出来,认真观察。
5、新知识的应用
请在下面的直角坐标系中,写出A、B、C、D、E、O的坐标
A(__,__)B(__,__)C(__,__)D(__,__)E(__,__)O(__,__)
(图2)
6、概念解析
在坐标平面内,两条互相垂直的坐标轴可以把坐标平面分为四个各部分,如图1,从右上角开始按逆时针方向,分别称为第一象限、第二象限、第三象限、第四象限,这时应注意坐标轴上的点不属于任何象限。现在请根据坐标系中点的坐标的定义,思考一下,各部分点的坐标的特点,如第一象限(+,+)。
试填空:第二象限( , )第三象限( , )第三象限( , )第四象限( , )x轴上( , )y轴上( , )
三、学习小结
同学们,你们本节课学到了哪些知识,请总结一下:
_______________________________________________________________________
___________________________________________________________________
四、达标检测
(一)、选择题(每题3分)
1、下列各点中,在第二象限的点是 ( )
A.(2,3) B.(2,-3) C.(-2,3) D.(-2, -3)
2、已知坐标平面内点M(a,b)在第三象限,那么点N(b, -a)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3、点P位于x轴下方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度,那么点P的坐标是 ( )
A.(4,2) B.(-2,-4) C.(-4,-2) D.(2,4)
4、点E(a,b)到x轴的距离是4,到y轴距离是3,则有 ( )
A.a=3, b=4 B.a=±3,b=±4 C.a=4, b=3 D.a=±4,b=±3
(二)解答题
点A(0,-3),点B(0,-4),点C在x轴上,如果△ABC的面积为15,求点C的坐标.(提示:C点在x轴上的位置有两个)
反思:
_______________________________________________________________________
_______________________________________________________________________
______________________________________________________________________。
