北京市密云区2021-2022学年高三上学期期末物理模拟试卷(1) (Word版含答案)
文档属性
| 名称 | 北京市密云区2021-2022学年高三上学期期末物理模拟试卷(1) (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 866.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-05 15:54:45 | ||
图片预览




文档简介
2021-2022学年北京市密云区高三(上)期末物理模拟试卷(1)
一.多选题(共10小题,满分30分,每小题3分)
1.(3分)如图所示为两点电荷a、b所形成电场的电场线分布图,有一带电粒子仅在电场力的作用下沿虚线运动,先后经过虚线上A、B、C三点,则下列说法正确的是( )
A.带电粒子的加速度大小aA>aB>aC
B.带电粒子的电势能先减小后增大
C.a、b两点电荷的电荷量大小qa<qb
D.三点的电势大小满足φC>φB>φA
2.(3分)以下所用物理学研究方法的叙述,正确的是( )
A.用质点来代替物体,是建立理想模型法
B.v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是类比法
C.当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法
D.认为空气中由静止开始下落的苹果做自由落体运动,是控制变量法
3.(3分)如图所示,理想变压器的原线圈接在u=220sin100πt(V)的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表。下列说法正确的是( )
A.电流表的读数为1.00 A B.电流表的读数为2.00A
C.电压表的读数为110V D.电压表的读数为155V
4.(3分)如图所示,当磁场的磁感应强度B增强时,则金属环有( )
A.顺时针的感应电流 B.逆时针的感应电流
C.收缩的趋势 D.扩张的趋势
5.(3分)如图电路中,电阻R随温度升高均匀增大,用这个电阻做探头测温,把电流表的刻度改为相应的温度刻度。下列说法正确的是( )
A.低温对应电流较大的刻度上,且温度刻度均匀
B.低温对应电流较大的刻度上,且温度刻度不均匀
C.高温对应电流较大的刻度上,且温度刻度均匀
D.高温对应电流较大的刻度上,且温度刻度不均匀
6.(3分)智能手机耗电量大,移动充电宝应运而生,它是能直接给移动设备充电的储能装置。充电宝的转化率是指电源放电总量占电源容量的比值,一般在0.60﹣0.70之间(包括移动电源和被充电池的线路板、接头和连线的损耗)。如图为某一款移动充电宝,其参数见如表,下列说法正确的是( )
容量 20000mAh 兼容性 所有智能手机
输入 DC5V2AMAX 输出 DC5V0.1﹣2.5A
尺寸 156*82*22mm 转换率 0.60
产品名称 索扬 重量 约430g
A.给充电宝充电时将大部分电能转化为化学能
B.该充电宝最多能储存能量为20000mAh
C.理论上该充电宝电量从零到完全充满电的时间约为10h
D.该充电宝给电量为零、容量为3000mAh的手机充电,则理论上能充满4次
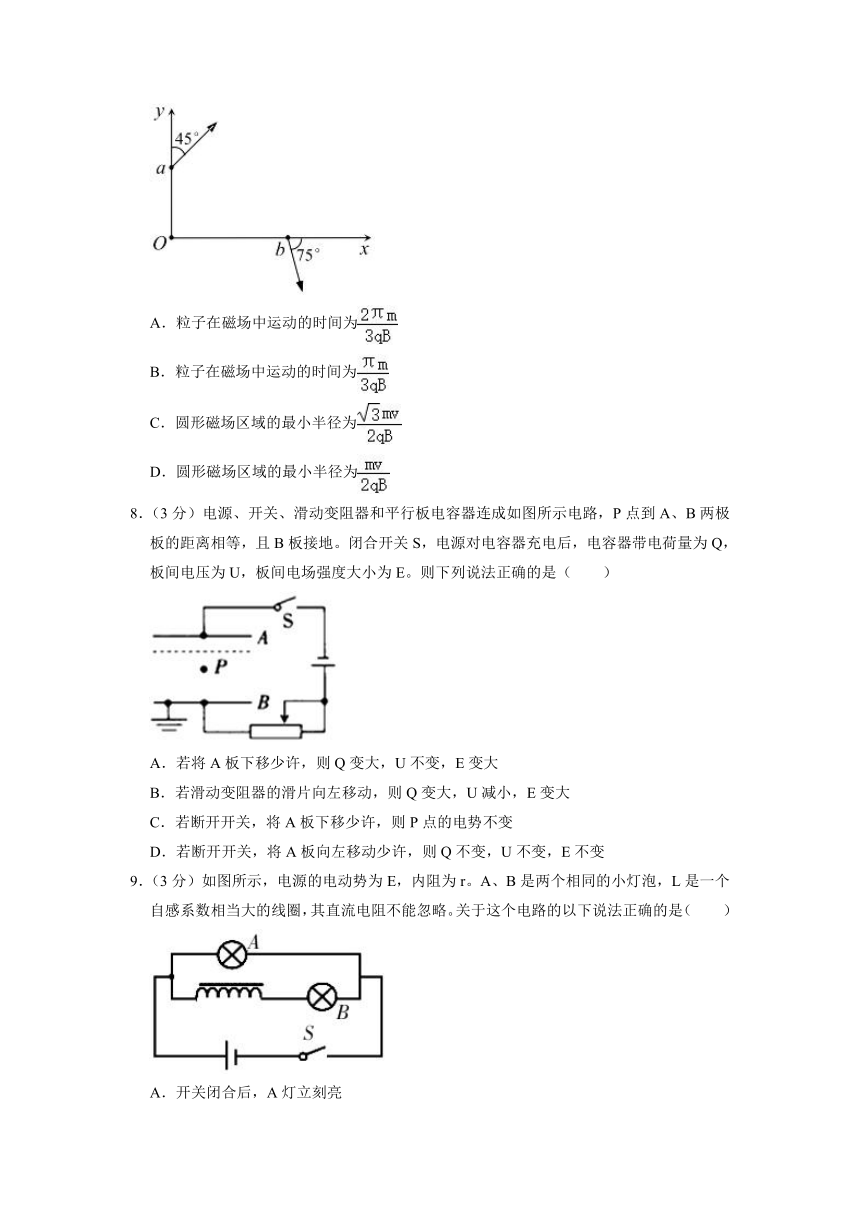
7.(3分)如图所示,一个带电粒子从y轴上的a点沿xOy平面且与y轴成45°角的方向进入xOy平面内,粒子经过垂直于xOy平面的圆形匀强磁场区域后从x轴上的b点射出,射出方向与x轴成75°角。已知带电粒子的质量为m、电荷量为q,带电粒子的运动速率为v,磁场的磁感应强度大小为B,不计粒子的重力,则下列说法正确的是( )
A.粒子在磁场中运动的时间为
B.粒子在磁场中运动的时间为
C.圆形磁场区域的最小半径为
D.圆形磁场区域的最小半径为
8.(3分)电源、开关、滑动变阻器和平行板电容器连成如图所示电路,P点到A、B两极板的距离相等,且B板接地。闭合开关S,电源对电容器充电后,电容器带电荷量为Q,板间电压为U,板间电场强度大小为E。则下列说法正确的是( )
A.若将A板下移少许,则Q变大,U不变,E变大
B.若滑动变阻器的滑片向左移动,则Q变大,U减小,E变大
C.若断开开关,将A板下移少许,则P点的电势不变
D.若断开开关,将A板向左移动少许,则Q不变,U不变,E不变
9.(3分)如图所示,电源的电动势为E,内阻为r。A、B是两个相同的小灯泡,L是一个自感系数相当大的线圈,其直流电阻不能忽略。关于这个电路的以下说法正确的是( )
A.开关闭合后,A灯立刻亮
B.开关闭合后,B灯立刻亮,而后逐渐变暗,最后亮度稳定
C.开关断开后瞬间,A灯左端电势比右端电势低
D.开关断开后瞬间,A灯闪亮一下再熄灭,B灯立即熄灭
10.(3分)如图所示,静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线。一个带负电的粒子在电场中以x=0为中心,沿x轴方向在区间[﹣A,A]之间做周期性运动,A<d.若φ0、d、A为已知量,且已知该粒子的比荷为.利用这些数据结合图象可以得出( )
A.该电场为匀强电场,且电场强度大小为
B.粒子运动时的加速度大小为
C.在x=0处粒子速度最大,为
D.粒子做周期性运动,且运动周期为
二.填空题(共2小题,满分15分)
11.(3分)一只电流表表头G的满偏电流为Ig=3mA,内阻为Rg=100Ω。若改装成量程为I=300mA的电流表,则改装后的电流表内阻为 Ω;若改装成量程为U=15V的电压表,则改装后的电压表内阻为 Ω。
12.(12分)某实验小组利用如图甲所示的电路图测定一电源的电动势(大约为6V)和内电阻。要求尽量减小实验误差。
(1)在下列两个电压表中选择一个最合适的来改装成量程为0~9V的电压表。
①量程为0~2V、内阻为2kΩ的电压表
②量程为0~3V、内阻为3kΩ的电压表
则应选择电压表 ,且串联一个阻值为 kΩ的电阻,就可以改装成量程为0~9V的电压表。
(2)现有电流表(0~0.6A),开关和导线若干,以及以下器材:
A.滑动变阻器R1(0~50Ω)
B.滑动变阻器R2(0~500Ω)
实验中滑动变阻器应选用 (填相应器材前的代号)。
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图乙的坐标纸上,请标出余下一组数据的对应点,并在坐标纸上正确作出U﹣I图线。
序号 1 2 3 4 5 6
电压U(V) 5.80 5.60 5.20 5.00 4.80 4.40
电流I(A) 0.060 0.120 0.240 0.260 0.360 0.480
(4)根据(3)中所画图线,可得出该电源的电动势E= V,内电阻r= Ω(结果均保留两位有效数字)。
(5)本次实验中,由于系统误差导致所测得的电源电动势 (填“偏大”“偏小”或”不变”)。
内阻 (填“偏大”“偏小”或“不变”)。
三.计算题(共7小题,满分65分)
13.(8分)如图所示,在水平面上固定有两平行长直导轨,右端接一电阻R═1.2Ω导轨内有一方向竖直向上、磁感应强度大小B=0.5T的匀强磁场。磁场区域为曲线方程y=sin(x)(x、y的单位均为m)与x轴所围的空间,其中0≤x≤4m,一电阻r=0.3Ω、长度L=1.2m的金属棒ab垂直搁在导轨上并在水平拉力作用下从x=0处以速度v=3m/s沿x轴正方向做匀速直线运动。导轨电阻不计,取g=10m/s2,求:
(1)ab两端电压的最大值Um;
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q。
14.(8分)氢原子由一个质子(原子核)和一个核外电子组成。电子质量me=9.1×10﹣31kg,质子质量mp=1.67×10﹣27kg,电子和原子核所带电荷量都等于e=1.6×10﹣19C。电子绕核旋转的轨道半径r=5.3×10﹣11m。试求:电子所受静电引力是万有引力的多少倍?
15.(8分)如图所示,长为L=1m的平行金属板水平放置,两极板带等量的异种电荷,板间形成竖直方向的匀强电场,一个质量为m=4×10﹣3kg,电量为q=2×10﹣6C的带负电荷的粒子,以初速度v0=4m/s紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与入射方向成37°,不计粒子重力,sin37°=0.6,cos37°=0.8。求:
(1)粒子射出下极板边缘时的动能;
(2)匀强电场的场强E的大小和方向。
16.(9分)间距为L的两平行光滑金属导轨如图所示,x轴平行导轨,y轴垂直导轨。在x=﹣x1位置有一宽度可不计的绝缘薄层,隔开左右两部分电路。在导轨间存在磁场,y轴左侧磁场方向垂直纸面向外,y轴右侧磁场方向垂直纸面向里,x<﹣x1区域磁场恒为B0,﹣x1≤x≤x0区域磁感应强度沿y轴方向磁感应强度大小不变,沿x轴方向磁感应强度大小随x变化,而且变化规律相同,在x=x0处磁感应强度大小为B0.导轨右侧的恒流源在开关S接通时为电路提供恒定的电流I(方向如图中箭头所示);导轨左侧接一阻值为R的电阻。有阻值为R的金属棒ab垂直导轨静止于x0处,当开关S接通时发现其在y轴右侧的位移随时间的变化规律为x=x0cosωt,其中为ω为已知常数,且2|﹣x1|=x0。
(1)金属棒ab的质量m为多少;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为多少。
17.(10分)如图所示,足够长的平行光滑金属导轨固定在水平面上,间距为L,一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B.电阻为r的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的恒力F作用下,导体棒沿导轨向右匀速运动,速度大小为v。
(1)求导体棒两端的电压;
(2)通过公式推导验证:在△t时间内,恒力F所做的功W等于电路获得的电能W电,也等于电路中产生的焦耳热Q;
(3)从微观角度看,导体棒MN中的自由电荷会同时参与沿导体棒方向和垂直导体棒方向的两个分运动,由此会受到两个相应的洛伦兹力,请你通过计算证明:导体棒中一个自由电荷所受的洛伦兹力做的总功为零。(为了方便,可认为导体棒中的自由电荷为正电荷。)
18.(10分)如图所示,在同一水平面的两导轨相互平行,相距2m并处于竖直向上的磁感应强度为B=0.75T的匀强磁场中,一根质量为1kg的金属棒放在导轨上且与导轨垂直。当金属棒中通如图所示的电流为5A时,金属棒恰好做匀速直线运动,最大静摩擦力等于滑动摩擦力。(g取10m/s2)求:
(1)导轨与金属棒间动摩擦因数;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度;
(3)若在竖直平面内改变磁感应强度的大小和方向,使金属棒刚好向ac端移动,则所加磁场的磁感应强度最小值和方向?
19.(12分)粒子加速器是借助于不同形态的电场,将带电粒子加速到高能量的电磁装置。粒子加速器可分为直线加速器和圆形加速器等类型。
(1)图1为多级直线加速器示意图。横截面积相同、长度依次增加的金属圆筒沿轴线依次排列,各筒相间地连接到交变电源的A、B两极,两极间电压uAB随时间的变化规律如图2所示。t=0时,序号为0的金属圆板中央一个质量为m、电荷量为+q的粒子,在圆板和圆筒之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。已知交变电源电压的绝对值为U,周期为T,带电粒子的重力和通过圆筒间隙的时间忽略不计。如果带电粒子每次经过圆筒之间都能被加速,求第n个圆筒的长度Ln;
(2)回旋加速器使带电粒子沿近似圆形的轨道运动,改进了直线加速器占地较大的问题。回旋加速器的工作原理如图3所示。半径为R的高真空的D形金属盒处在匀强磁场中,磁感应强度大小为B,方向与盒面垂直。将两盒与电压为U的高频交变电源相连,两盒的狭缝间形成周期性变化的电场。A处粒子源产生的带电粒子,质量为m、电荷量为+q,初速度为0。调整交流电源的频率可使粒子每次通过狭缝时都能被加速。不计带电粒子穿过狭缝的时间和粒子所受重力。求:
①所加交流电的频率f;
②粒子获得的最大动能Ekm。
(3)对于质量较小的电子,由于受到相对论效应的影响,回旋加速器就不适用了。加速电子可以用电子感应加速器。图4是其结构图(上为侧视图,下为真空室俯视图),圆形电磁铁两极间有一环形真空室,在交变电流的激励下,两极间出现交变磁场,交变磁场又激发出感生电场。从电子枪射入真空室的电子在感生电场力和洛伦兹力的共同作用下,在真空室内做加速圆周运动,加速完成后,电子束被引离轨道进入靶室。图5为一周期内磁场的变化情况,B为正时表示B的方向竖直向上。已知电子带负电,试简要分析在一周期内的哪段时间内,电子可被加速做圆周运动?
2021-2022学年北京市密云区高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.多选题(共10小题,满分30分,每小题3分)
1.(3分)如图所示为两点电荷a、b所形成电场的电场线分布图,有一带电粒子仅在电场力的作用下沿虚线运动,先后经过虚线上A、B、C三点,则下列说法正确的是( )
A.带电粒子的加速度大小aA>aB>aC
B.带电粒子的电势能先减小后增大
C.a、b两点电荷的电荷量大小qa<qb
D.三点的电势大小满足φC>φB>φA
【解答】解:A、电场线的疏密表示电场的强弱,由图知EA<EB<EC,由F=qE得:FA<FB<FC,由牛顿第二定律a=得:aA<aB<aC,故A错误;
B、物体做曲线运动时轨迹向合力一侧弯曲,速度沿切线方向,从A到B,电场力对粒子做正功,电势能减小;从B到C,电场力对粒子做负功,电势能增大,故B正确;
C、由轨迹可知a对粒子是引力,b对粒子是斥力,从B到C弯曲程度加大,b对粒子的斥力大于a对粒子的引力,且粒子到a的距离小于到b的距离,由库仑定律可知:
qa<qb,故C正确;
D、由于a、b的电性不确定,无法比较三点的电势高低,故D错误。
故选:BC。
2.(3分)以下所用物理学研究方法的叙述,正确的是( )
A.用质点来代替物体,是建立理想模型法
B.v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是类比法
C.当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法
D.认为空气中由静止开始下落的苹果做自由落体运动,是控制变量法
【解答】解:A、质点采用的科学方法为建立理想化的物理模型法,故A正确;
B、v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是微元法,故B错误;
C、当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法,故C正确;
D、认为空气中由静止开始下落的苹果做自由落体运动,是理想模型法,故D错误;
故选:AC。
3.(3分)如图所示,理想变压器的原线圈接在u=220sin100πt(V)的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表。下列说法正确的是( )
A.电流表的读数为1.00 A B.电流表的读数为2.00A
C.电压表的读数为110V D.电压表的读数为155V
【解答】解:AB、由瞬时值的表达式可得,原线圈的电压有效值为220V,根据电压与匝数成正比可得,副线圈的电压为110V,再由输入功率和输出功率相等可得220I1=W,所以原线圈的电流的大小为1.00A,电流表读数为1.00A,故A正确,B错误。
CD、电压表的读数为电压的有效值,由A的分析可知,副线圈的有效值为110V,所以电压表的读数为110V,故C正确,D错误。
故选:AC。
4.(3分)如图所示,当磁场的磁感应强度B增强时,则金属环有( )
A.顺时针的感应电流 B.逆时针的感应电流
C.收缩的趋势 D.扩张的趋势
【解答】解:AB、当磁场的磁感应强度B增强时,穿过闭合回路的磁通量向里增加,根据楞次定律,感应电流的磁场方向向外,根据安培定则,感应电流为逆时针方向,故A错误,B正确。
CD、穿过闭合回路的磁通量增加,根据楞次定律,环有收缩的趋势,故C正确,D错误。
故选:BC。
5.(3分)如图电路中,电阻R随温度升高均匀增大,用这个电阻做探头测温,把电流表的刻度改为相应的温度刻度。下列说法正确的是( )
A.低温对应电流较大的刻度上,且温度刻度均匀
B.低温对应电流较大的刻度上,且温度刻度不均匀
C.高温对应电流较大的刻度上,且温度刻度均匀
D.高温对应电流较大的刻度上,且温度刻度不均匀
【解答】解:根据图示电路图结合闭合电路的欧姆定律得:E=I(r+R+RA),
解得电路的电流为:I=,可见电阻R越小,电流I越大,对应的温度越低,所以低温对应电流较大的刻度上;
由于电阻R随温度升高均匀增大,则电阻R与温度的变化为:R=R0+kt(k>0),
解得:t=(RA+r+R0),所以t与I不是线性关系,温度刻度不均匀,故B正确、ACD错误。
故选:B。
6.(3分)智能手机耗电量大,移动充电宝应运而生,它是能直接给移动设备充电的储能装置。充电宝的转化率是指电源放电总量占电源容量的比值,一般在0.60﹣0.70之间(包括移动电源和被充电池的线路板、接头和连线的损耗)。如图为某一款移动充电宝,其参数见如表,下列说法正确的是( )
容量 20000mAh 兼容性 所有智能手机
输入 DC5V2AMAX 输出 DC5V0.1﹣2.5A
尺寸 156*82*22mm 转换率 0.60
产品名称 索扬 重量 约430g
A.给充电宝充电时将大部分电能转化为化学能
B.该充电宝最多能储存能量为20000mAh
C.理论上该充电宝电量从零到完全充满电的时间约为10h
D.该充电宝给电量为零、容量为3000mAh的手机充电,则理论上能充满4次
【解答】解:A、给充电宝充电时是把电能转化为化学能的过程,故A正确;
B、该充电宝的容量为:q=20000mAh=20000×10﹣3×3600=7.2×104C,
该电池的电动势为5V,所以充电宝储存的能量:E=E电动势 q=5×7.2×104=3.6×105J;故B错误;
C、该充电宝的容量为:q=20000mAh=2000×10﹣3×3600=7.2×104C
以2A的电流为用电器供电则供电时间t==10h,故C正确。
D、由于充电宝的转化率是0.6,所以可以释放的电能为:20000mA h×0.6=12000mAh,给容量为3000mAh的手机充电的次数:n=4,故D正确。
故选:ACD。
7.(3分)如图所示,一个带电粒子从y轴上的a点沿xOy平面且与y轴成45°角的方向进入xOy平面内,粒子经过垂直于xOy平面的圆形匀强磁场区域后从x轴上的b点射出,射出方向与x轴成75°角。已知带电粒子的质量为m、电荷量为q,带电粒子的运动速率为v,磁场的磁感应强度大小为B,不计粒子的重力,则下列说法正确的是( )
A.粒子在磁场中运动的时间为
B.粒子在磁场中运动的时间为
C.圆形磁场区域的最小半径为
D.圆形磁场区域的最小半径为
【解答】解:AB、根据几何知识知速度偏转角为:θ=45°+75°=120°
粒子在磁场中的周期为:T=
所以粒子在磁场中运动的时间为:t==,故A正确,B错误;
CD、连接ab为圆周运动的弦,根据几何知识知磁场最小半径为:R=ab=rsin60°==,故C正确,D错误。
故选:AC。
8.(3分)电源、开关、滑动变阻器和平行板电容器连成如图所示电路,P点到A、B两极板的距离相等,且B板接地。闭合开关S,电源对电容器充电后,电容器带电荷量为Q,板间电压为U,板间电场强度大小为E。则下列说法正确的是( )
A.若将A板下移少许,则Q变大,U不变,E变大
B.若滑动变阻器的滑片向左移动,则Q变大,U减小,E变大
C.若断开开关,将A板下移少许,则P点的电势不变
D.若断开开关,将A板向左移动少许,则Q不变,U不变,E不变
【解答】解:A、保持开关闭合,则极板间电压U不变,若将A板下移少许,即减小极板间距d,由C= 可知,电容器的电容增大;由Q=UC可知,Q增大,由E0= 可知,电场强度变大,故A正确;
B、因滑动变阻器与电容器串联接在电源上,其变阻器相当于导线,则滑片的移动不会改变电路电压,则Q、U及E均不变,故B错误;
CD、给电容器充电后与电源断开,电量Q不变,若将A板下移少许,即减小极板间距,由C= 可知,电容器的电容增大;由Q=UC可知,U减小,由E0== 可知,E0不变,所以P点到下极板的电压不变,则P点的电势也不变,故C正确,D错误。
故选:AC。
9.(3分)如图所示,电源的电动势为E,内阻为r。A、B是两个相同的小灯泡,L是一个自感系数相当大的线圈,其直流电阻不能忽略。关于这个电路的以下说法正确的是( )
A.开关闭合后,A灯立刻亮
B.开关闭合后,B灯立刻亮,而后逐渐变暗,最后亮度稳定
C.开关断开后瞬间,A灯左端电势比右端电势低
D.开关断开后瞬间,A灯闪亮一下再熄灭,B灯立即熄灭
【解答】解:A、开关闭合到瞬间电压直接加到灯泡A上,所以开关闭合到电路中电流稳定的时间内,A灯立刻亮,故A正确;
B、开关闭合到电路中电流稳定的时间内,线圈开始时产生自感电动势,自感电动势随对电流阻碍较小后B灯逐渐变亮,当线圈对电流没有阻碍时,灯泡B亮度稳定,故B错误;
C、开关处于闭合状态,在断开瞬间,线圈相当于电源,电流方向仍不变,所以电流自右向左通过A灯,A灯左端电势比右端电势低,故C正确;
D、开关处于闭合状态,在断开瞬间,线圈与两个灯泡组成自感回路,由于两灯泡完全一样,所以不会出现电流比之前还大的现象,因此A灯不会闪亮一下,只会与B一起慢慢熄灭,故D错误;
故选:AC。
10.(3分)如图所示,静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线。一个带负电的粒子在电场中以x=0为中心,沿x轴方向在区间[﹣A,A]之间做周期性运动,A<d.若φ0、d、A为已知量,且已知该粒子的比荷为.利用这些数据结合图象可以得出( )
A.该电场为匀强电场,且电场强度大小为
B.粒子运动时的加速度大小为
C.在x=0处粒子速度最大,为
D.粒子做周期性运动,且运动周期为
【解答】解:A、由图可知,0与d(或﹣d)两点间的电势差为φ0,电势随x均匀变化,电场为匀强电场,则电场强度的大小为:E=,故A正确。
B、粒子所受的电场力的大小为F=qE,由牛顿第二定律得:加速度为a==,故B错误;
C、粒子经过x=0时速度最大,设其大小为v,从A到O过程,由动能定理得:
qEA=mv2
解得:v==,故C正确。
D、粒子从x=0处开始运动的四分之一周期内做匀加速直线运动,用时t=,粒子完成一次往复运动的时间为 T=4t,运动周期为T=4,故D正确。
故选:ACD。
二.填空题(共2小题,满分15分)
11.(3分)一只电流表表头G的满偏电流为Ig=3mA,内阻为Rg=100Ω。若改装成量程为I=300mA的电流表,则改装后的电流表内阻为 1 Ω;若改装成量程为U=15V的电压表,则改装后的电压表内阻为 5000 Ω。
【解答】解:改装成电流表时需要并联小电阻,改装后电压等于电流表的满偏电压Ug=0.003×100V=0.3V;总电流I=300mA=0.3A;由欧姆定律可得,改装后电流表内阻R1==Ω=1Ω;
改装成电压表时需要串联大电阻,电路中电流为满偏电流Ig=3mA=0.003A,此时串联部分电压U=15V,由欧姆定律可得,R==Ω=5000Ω。
故答案为:1;5000。
12.(12分)某实验小组利用如图甲所示的电路图测定一电源的电动势(大约为6V)和内电阻。要求尽量减小实验误差。
(1)在下列两个电压表中选择一个最合适的来改装成量程为0~9V的电压表。
①量程为0~2V、内阻为2kΩ的电压表
②量程为0~3V、内阻为3kΩ的电压表
则应选择电压表 ② ,且串联一个阻值为 6 kΩ的电阻,就可以改装成量程为0~9V的电压表。
(2)现有电流表(0~0.6A),开关和导线若干,以及以下器材:
A.滑动变阻器R1(0~50Ω)
B.滑动变阻器R2(0~500Ω)
实验中滑动变阻器应选用 A (填相应器材前的代号)。
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图乙的坐标纸上,请标出余下一组数据的对应点,并在坐标纸上正确作出U﹣I图线。
序号 1 2 3 4 5 6
电压U(V) 5.80 5.60 5.20 5.00 4.80 4.40
电流I(A) 0.060 0.120 0.240 0.260 0.360 0.480
(4)根据(3)中所画图线,可得出该电源的电动势E= 6.0 V,内电阻r= 3.3 Ω(结果均保留两位有效数字)。
(5)本次实验中,由于系统误差导致所测得的电源电动势 偏小 (填“偏大”“偏小”或”不变”)。
内阻 偏小 (填“偏大”“偏小”或“不变”)。
【解答】解:(1)应选择量程为0~3V、内阻为3kΩ的电压表②进行改装,改装后量程与内阻都扩大3倍,根据串联电路特点可知,串联分压电阻阻值为原电表内阻的2倍,串联电阻阻值为6kΩ。
(2)电源电动势约为6V,电流表量程为0.6A,电路最小电阻约为R=Ω=10Ω,为方便实验操作,滑动变阻器应选择A。
(3)根据表中实验数据在坐标系内描出对应点,让尽可能多的点过直线,不能过直线的点对称分布在直线两侧,偏离直线太远的点应舍去,根据坐标系内描出的点作出图象如图所示;
(4)由图甲所示可知,路端电压U=E﹣Ir,由图示电源UI图象可知,电源电动势E=6.0V,内阻r=Ω≈3.3Ω。
(5)由图甲所示电路图可知,当外电路短路时,电流的测量值等于真实值,除此之外,由于电压表的分流作用,电流的测量值小于真实值,电源的U﹣I图象如图所示,由图象可知,电源电动势的测量值小于真实值,电源内阻测量值小于真实值.
故答案为:(1)②;6;(2)A;(3)图象如图所示;(4)6.0;3.3;(5)偏小;偏小。
三.计算题(共7小题,满分65分)
13.(8分)如图所示,在水平面上固定有两平行长直导轨,右端接一电阻R═1.2Ω导轨内有一方向竖直向上、磁感应强度大小B=0.5T的匀强磁场。磁场区域为曲线方程y=sin(x)(x、y的单位均为m)与x轴所围的空间,其中0≤x≤4m,一电阻r=0.3Ω、长度L=1.2m的金属棒ab垂直搁在导轨上并在水平拉力作用下从x=0处以速度v=3m/s沿x轴正方向做匀速直线运动。导轨电阻不计,取g=10m/s2,求:
(1)ab两端电压的最大值Um;
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q。
【解答】解:(1)金属棒ab切割感线最大的长度为 ym=1.0m
金属棒ab中产生的感应电动势的最大值为 Em=Bymv
根据闭合电路欧姆定律有 Im=
ab两端电压的最大值为 Um=ImR
联立解得 Um=1.2V
(2)金属棒ab在磁场中切割磁感线产生的感应电动势瞬时值为:e=Byv
上式中 y=sin(x)(m),其中 x=vt
解得 e=1.5sint(V)
可知感应电动势的最大值为 Em=1.5V
有效值为 E=
金属棒ab在磁场中运动的时间为 t=,其中 x0=4m
这段时间内回路中产生的总焦耳热为 Q=t
解得 Q=1J
答:(1)ab两端电压的最大值Um是1.2V。
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q是1J。
14.(8分)氢原子由一个质子(原子核)和一个核外电子组成。电子质量me=9.1×10﹣31kg,质子质量mp=1.67×10﹣27kg,电子和原子核所带电荷量都等于e=1.6×10﹣19C。电子绕核旋转的轨道半径r=5.3×10﹣11m。试求:电子所受静电引力是万有引力的多少倍?
【解答】解:根据仑定律得库仑力大小:
F电=k=8.2×10﹣8N
根据万有引力定律得万有引力大小:
F万=G=3.6×10﹣47N,
所以
=2.28×1039。
答:电子所受静电引力是万有引力的2.28×1039倍。
15.(8分)如图所示,长为L=1m的平行金属板水平放置,两极板带等量的异种电荷,板间形成竖直方向的匀强电场,一个质量为m=4×10﹣3kg,电量为q=2×10﹣6C的带负电荷的粒子,以初速度v0=4m/s紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与入射方向成37°,不计粒子重力,sin37°=0.6,cos37°=0.8。求:
(1)粒子射出下极板边缘时的动能;
(2)匀强电场的场强E的大小和方向。
【解答】解:(1)粒子离开电场时,合速度与水平夹角为37°,如图所示
粒子射出下极板边缘时速度大小为:
射出电场时动能为:Ek=
两式联立解得:;
(2)粒子在匀强电场中做类平抛运动
水平方向:L=v0t
竖直方向:vy=at=t
又有:
解得:
代入数据得:E=2.4×104V/m
根据已知条件粒子所受电场力竖直向下,又因为粒子带负点,负电荷受力的方向与场强的方向相反,故匀强电场的方向竖直向上。
答:(1)粒子射出下极板边缘时的动能为5×10﹣2J;
(2)匀强电场的场强E的大小为2.4×104V/m,方向竖直向上。
16.(9分)间距为L的两平行光滑金属导轨如图所示,x轴平行导轨,y轴垂直导轨。在x=﹣x1位置有一宽度可不计的绝缘薄层,隔开左右两部分电路。在导轨间存在磁场,y轴左侧磁场方向垂直纸面向外,y轴右侧磁场方向垂直纸面向里,x<﹣x1区域磁场恒为B0,﹣x1≤x≤x0区域磁感应强度沿y轴方向磁感应强度大小不变,沿x轴方向磁感应强度大小随x变化,而且变化规律相同,在x=x0处磁感应强度大小为B0.导轨右侧的恒流源在开关S接通时为电路提供恒定的电流I(方向如图中箭头所示);导轨左侧接一阻值为R的电阻。有阻值为R的金属棒ab垂直导轨静止于x0处,当开关S接通时发现其在y轴右侧的位移随时间的变化规律为x=x0cosωt,其中为ω为已知常数,且2|﹣x1|=x0。
(1)金属棒ab的质量m为多少;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为多少。
【解答】解:(1)对x=x0cosωt求导有:v=﹣ωx0sinωt,
再对v求导得:
当t=0时:
故得 ;
(2)由x0→x1过程:
流过金属棒ab的电量
由x1到最左端:
又根据动量定理得
﹣B0lt2=0﹣mv1
又 t2=qt2
则得﹣B0q2l=0﹣mv1
故 ;
因此,金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量 ;
(3)由x0→﹣x1过程:
﹣x1到最左边过程:
则。
答:(1)金属棒ab的质量m为得 ;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量为 ;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为。
17.(10分)如图所示,足够长的平行光滑金属导轨固定在水平面上,间距为L,一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B.电阻为r的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的恒力F作用下,导体棒沿导轨向右匀速运动,速度大小为v。
(1)求导体棒两端的电压;
(2)通过公式推导验证:在△t时间内,恒力F所做的功W等于电路获得的电能W电,也等于电路中产生的焦耳热Q;
(3)从微观角度看,导体棒MN中的自由电荷会同时参与沿导体棒方向和垂直导体棒方向的两个分运动,由此会受到两个相应的洛伦兹力,请你通过计算证明:导体棒中一个自由电荷所受的洛伦兹力做的总功为零。(为了方便,可认为导体棒中的自由电荷为正电荷。)
【解答】解:(1)导体棒沿导轨向右匀速运动产生感应电动势E = BLv
由闭合电路欧姆定律可得,电路中电流I=
导体棒两端电压U=IR=;
(2)导体棒匀速运动,受力平衡F=FA=BIL
在△t时间内,
恒力F做功W=Fv△t=FAv△t=BILv△t=
电路获得的电能W电=qE=EI△t=
电路中产生的焦耳热Q=I2(R+r)△t=
可见,恒力F所做的功等于电路获得的电能W电,也等于电路中产生的焦耳热Q。
(3)设自由电荷的电荷量为q,沿导体棒定向移动的速率为u。
沿导体棒方向的洛伦兹力f1=qvB
在△t时间内,f1做正功Q1=f1u△t=qvBu△t
垂直导体棒方向的洛伦兹力f2=qvB
在△t时间内,f2做负功W2=﹣f2 u△t=﹣quBv△t
所以W1+W2=0,即导体棒中一个自由电荷所受的洛伦兹力做的总功为零。
答:(1)导体棒两端的电压为;
(2)推导过程见解析;
(3)证明见解析。
18.(10分)如图所示,在同一水平面的两导轨相互平行,相距2m并处于竖直向上的磁感应强度为B=0.75T的匀强磁场中,一根质量为1kg的金属棒放在导轨上且与导轨垂直。当金属棒中通如图所示的电流为5A时,金属棒恰好做匀速直线运动,最大静摩擦力等于滑动摩擦力。(g取10m/s2)求:
(1)导轨与金属棒间动摩擦因数;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度;
(3)若在竖直平面内改变磁感应强度的大小和方向,使金属棒刚好向ac端移动,则所加磁场的磁感应强度最小值和方向?
【解答】解:(1)金属棒受到的安培力:F=BIL,
由平衡条件得:μmg=BIL,
代入数据得:μ=0.75;
(2)金属棒受到的安培力:F′=BI′L,
由牛顿第二定律得:BI′L﹣μmg=ma,
代入数据得:a=6m/s2;
(3)金属棒刚好向ac端移动且磁感应强度最小时,
由平衡条件得:B′IL=mg,
代入数据得:B′=1T,
根据左手定则可知,磁感应强度方向水平向左;
答:(1)导轨与金属棒间动摩擦因数为0.75;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度6m/s2;
(3)所加磁场的磁感应强度最小值为1T,方向:水平向左。
19.(12分)粒子加速器是借助于不同形态的电场,将带电粒子加速到高能量的电磁装置。粒子加速器可分为直线加速器和圆形加速器等类型。
(1)图1为多级直线加速器示意图。横截面积相同、长度依次增加的金属圆筒沿轴线依次排列,各筒相间地连接到交变电源的A、B两极,两极间电压uAB随时间的变化规律如图2所示。t=0时,序号为0的金属圆板中央一个质量为m、电荷量为+q的粒子,在圆板和圆筒之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。已知交变电源电压的绝对值为U,周期为T,带电粒子的重力和通过圆筒间隙的时间忽略不计。如果带电粒子每次经过圆筒之间都能被加速,求第n个圆筒的长度Ln;
(2)回旋加速器使带电粒子沿近似圆形的轨道运动,改进了直线加速器占地较大的问题。回旋加速器的工作原理如图3所示。半径为R的高真空的D形金属盒处在匀强磁场中,磁感应强度大小为B,方向与盒面垂直。将两盒与电压为U的高频交变电源相连,两盒的狭缝间形成周期性变化的电场。A处粒子源产生的带电粒子,质量为m、电荷量为+q,初速度为0。调整交流电源的频率可使粒子每次通过狭缝时都能被加速。不计带电粒子穿过狭缝的时间和粒子所受重力。求:
①所加交流电的频率f;
②粒子获得的最大动能Ekm。
(3)对于质量较小的电子,由于受到相对论效应的影响,回旋加速器就不适用了。加速电子可以用电子感应加速器。图4是其结构图(上为侧视图,下为真空室俯视图),圆形电磁铁两极间有一环形真空室,在交变电流的激励下,两极间出现交变磁场,交变磁场又激发出感生电场。从电子枪射入真空室的电子在感生电场力和洛伦兹力的共同作用下,在真空室内做加速圆周运动,加速完成后,电子束被引离轨道进入靶室。图5为一周期内磁场的变化情况,B为正时表示B的方向竖直向上。已知电子带负电,试简要分析在一周期内的哪段时间内,电子可被加速做圆周运动?
【解答】解:(1)设带电粒子进入第n个圆筒时的速度为vn,根据动能定理有:nqU=
如果粒子匀速穿过每个圆筒的时间恰好等于交变电压周期的一半,那它每到达一个间隙都能被加速,有:Ln=vn×
解得:Ln=;
(2)①如果交变电源的频率等于粒子圆周运动的频率,那么粒子每次通过狭缝时都能被加速。
根据洛伦兹力提供向心力可得:qvB=m
交变电流的频率f==
解得:f=;
②粒子的速度与半径成正比,所以当圆周运动的半径最大时,粒子的动能最大。
根据洛伦兹力提供向心力可得:qvmB=m
解得:Ekm==;
(3)在第一个时间内,电子可被加速做圆周运动。
由楞次定律可知,在第一个和第四个时间内,感生电场的方向为顺时针方向,电子受力方向为逆时针方向,可被加速;
由左手定则可知,只有磁场方向向上时,电子所受洛伦兹力才指向圆心,充当向心力。
综合考虑,只有第一个时间内,电子可被加速做圆周运动。
答:(1)第n个圆筒的长度为;
(2)①所加交流电的频率为;
②粒子获得的最大动能为;
(3)只有第一个时间内,电子可被加速做圆周运动。
一.多选题(共10小题,满分30分,每小题3分)
1.(3分)如图所示为两点电荷a、b所形成电场的电场线分布图,有一带电粒子仅在电场力的作用下沿虚线运动,先后经过虚线上A、B、C三点,则下列说法正确的是( )
A.带电粒子的加速度大小aA>aB>aC
B.带电粒子的电势能先减小后增大
C.a、b两点电荷的电荷量大小qa<qb
D.三点的电势大小满足φC>φB>φA
2.(3分)以下所用物理学研究方法的叙述,正确的是( )
A.用质点来代替物体,是建立理想模型法
B.v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是类比法
C.当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法
D.认为空气中由静止开始下落的苹果做自由落体运动,是控制变量法
3.(3分)如图所示,理想变压器的原线圈接在u=220sin100πt(V)的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表。下列说法正确的是( )
A.电流表的读数为1.00 A B.电流表的读数为2.00A
C.电压表的读数为110V D.电压表的读数为155V
4.(3分)如图所示,当磁场的磁感应强度B增强时,则金属环有( )
A.顺时针的感应电流 B.逆时针的感应电流
C.收缩的趋势 D.扩张的趋势
5.(3分)如图电路中,电阻R随温度升高均匀增大,用这个电阻做探头测温,把电流表的刻度改为相应的温度刻度。下列说法正确的是( )
A.低温对应电流较大的刻度上,且温度刻度均匀
B.低温对应电流较大的刻度上,且温度刻度不均匀
C.高温对应电流较大的刻度上,且温度刻度均匀
D.高温对应电流较大的刻度上,且温度刻度不均匀
6.(3分)智能手机耗电量大,移动充电宝应运而生,它是能直接给移动设备充电的储能装置。充电宝的转化率是指电源放电总量占电源容量的比值,一般在0.60﹣0.70之间(包括移动电源和被充电池的线路板、接头和连线的损耗)。如图为某一款移动充电宝,其参数见如表,下列说法正确的是( )
容量 20000mAh 兼容性 所有智能手机
输入 DC5V2AMAX 输出 DC5V0.1﹣2.5A
尺寸 156*82*22mm 转换率 0.60
产品名称 索扬 重量 约430g
A.给充电宝充电时将大部分电能转化为化学能
B.该充电宝最多能储存能量为20000mAh
C.理论上该充电宝电量从零到完全充满电的时间约为10h
D.该充电宝给电量为零、容量为3000mAh的手机充电,则理论上能充满4次
7.(3分)如图所示,一个带电粒子从y轴上的a点沿xOy平面且与y轴成45°角的方向进入xOy平面内,粒子经过垂直于xOy平面的圆形匀强磁场区域后从x轴上的b点射出,射出方向与x轴成75°角。已知带电粒子的质量为m、电荷量为q,带电粒子的运动速率为v,磁场的磁感应强度大小为B,不计粒子的重力,则下列说法正确的是( )
A.粒子在磁场中运动的时间为
B.粒子在磁场中运动的时间为
C.圆形磁场区域的最小半径为
D.圆形磁场区域的最小半径为
8.(3分)电源、开关、滑动变阻器和平行板电容器连成如图所示电路,P点到A、B两极板的距离相等,且B板接地。闭合开关S,电源对电容器充电后,电容器带电荷量为Q,板间电压为U,板间电场强度大小为E。则下列说法正确的是( )
A.若将A板下移少许,则Q变大,U不变,E变大
B.若滑动变阻器的滑片向左移动,则Q变大,U减小,E变大
C.若断开开关,将A板下移少许,则P点的电势不变
D.若断开开关,将A板向左移动少许,则Q不变,U不变,E不变
9.(3分)如图所示,电源的电动势为E,内阻为r。A、B是两个相同的小灯泡,L是一个自感系数相当大的线圈,其直流电阻不能忽略。关于这个电路的以下说法正确的是( )
A.开关闭合后,A灯立刻亮
B.开关闭合后,B灯立刻亮,而后逐渐变暗,最后亮度稳定
C.开关断开后瞬间,A灯左端电势比右端电势低
D.开关断开后瞬间,A灯闪亮一下再熄灭,B灯立即熄灭
10.(3分)如图所示,静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线。一个带负电的粒子在电场中以x=0为中心,沿x轴方向在区间[﹣A,A]之间做周期性运动,A<d.若φ0、d、A为已知量,且已知该粒子的比荷为.利用这些数据结合图象可以得出( )
A.该电场为匀强电场,且电场强度大小为
B.粒子运动时的加速度大小为
C.在x=0处粒子速度最大,为
D.粒子做周期性运动,且运动周期为
二.填空题(共2小题,满分15分)
11.(3分)一只电流表表头G的满偏电流为Ig=3mA,内阻为Rg=100Ω。若改装成量程为I=300mA的电流表,则改装后的电流表内阻为 Ω;若改装成量程为U=15V的电压表,则改装后的电压表内阻为 Ω。
12.(12分)某实验小组利用如图甲所示的电路图测定一电源的电动势(大约为6V)和内电阻。要求尽量减小实验误差。
(1)在下列两个电压表中选择一个最合适的来改装成量程为0~9V的电压表。
①量程为0~2V、内阻为2kΩ的电压表
②量程为0~3V、内阻为3kΩ的电压表
则应选择电压表 ,且串联一个阻值为 kΩ的电阻,就可以改装成量程为0~9V的电压表。
(2)现有电流表(0~0.6A),开关和导线若干,以及以下器材:
A.滑动变阻器R1(0~50Ω)
B.滑动变阻器R2(0~500Ω)
实验中滑动变阻器应选用 (填相应器材前的代号)。
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图乙的坐标纸上,请标出余下一组数据的对应点,并在坐标纸上正确作出U﹣I图线。
序号 1 2 3 4 5 6
电压U(V) 5.80 5.60 5.20 5.00 4.80 4.40
电流I(A) 0.060 0.120 0.240 0.260 0.360 0.480
(4)根据(3)中所画图线,可得出该电源的电动势E= V,内电阻r= Ω(结果均保留两位有效数字)。
(5)本次实验中,由于系统误差导致所测得的电源电动势 (填“偏大”“偏小”或”不变”)。
内阻 (填“偏大”“偏小”或“不变”)。
三.计算题(共7小题,满分65分)
13.(8分)如图所示,在水平面上固定有两平行长直导轨,右端接一电阻R═1.2Ω导轨内有一方向竖直向上、磁感应强度大小B=0.5T的匀强磁场。磁场区域为曲线方程y=sin(x)(x、y的单位均为m)与x轴所围的空间,其中0≤x≤4m,一电阻r=0.3Ω、长度L=1.2m的金属棒ab垂直搁在导轨上并在水平拉力作用下从x=0处以速度v=3m/s沿x轴正方向做匀速直线运动。导轨电阻不计,取g=10m/s2,求:
(1)ab两端电压的最大值Um;
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q。
14.(8分)氢原子由一个质子(原子核)和一个核外电子组成。电子质量me=9.1×10﹣31kg,质子质量mp=1.67×10﹣27kg,电子和原子核所带电荷量都等于e=1.6×10﹣19C。电子绕核旋转的轨道半径r=5.3×10﹣11m。试求:电子所受静电引力是万有引力的多少倍?
15.(8分)如图所示,长为L=1m的平行金属板水平放置,两极板带等量的异种电荷,板间形成竖直方向的匀强电场,一个质量为m=4×10﹣3kg,电量为q=2×10﹣6C的带负电荷的粒子,以初速度v0=4m/s紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与入射方向成37°,不计粒子重力,sin37°=0.6,cos37°=0.8。求:
(1)粒子射出下极板边缘时的动能;
(2)匀强电场的场强E的大小和方向。
16.(9分)间距为L的两平行光滑金属导轨如图所示,x轴平行导轨,y轴垂直导轨。在x=﹣x1位置有一宽度可不计的绝缘薄层,隔开左右两部分电路。在导轨间存在磁场,y轴左侧磁场方向垂直纸面向外,y轴右侧磁场方向垂直纸面向里,x<﹣x1区域磁场恒为B0,﹣x1≤x≤x0区域磁感应强度沿y轴方向磁感应强度大小不变,沿x轴方向磁感应强度大小随x变化,而且变化规律相同,在x=x0处磁感应强度大小为B0.导轨右侧的恒流源在开关S接通时为电路提供恒定的电流I(方向如图中箭头所示);导轨左侧接一阻值为R的电阻。有阻值为R的金属棒ab垂直导轨静止于x0处,当开关S接通时发现其在y轴右侧的位移随时间的变化规律为x=x0cosωt,其中为ω为已知常数,且2|﹣x1|=x0。
(1)金属棒ab的质量m为多少;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为多少。
17.(10分)如图所示,足够长的平行光滑金属导轨固定在水平面上,间距为L,一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B.电阻为r的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的恒力F作用下,导体棒沿导轨向右匀速运动,速度大小为v。
(1)求导体棒两端的电压;
(2)通过公式推导验证:在△t时间内,恒力F所做的功W等于电路获得的电能W电,也等于电路中产生的焦耳热Q;
(3)从微观角度看,导体棒MN中的自由电荷会同时参与沿导体棒方向和垂直导体棒方向的两个分运动,由此会受到两个相应的洛伦兹力,请你通过计算证明:导体棒中一个自由电荷所受的洛伦兹力做的总功为零。(为了方便,可认为导体棒中的自由电荷为正电荷。)
18.(10分)如图所示,在同一水平面的两导轨相互平行,相距2m并处于竖直向上的磁感应强度为B=0.75T的匀强磁场中,一根质量为1kg的金属棒放在导轨上且与导轨垂直。当金属棒中通如图所示的电流为5A时,金属棒恰好做匀速直线运动,最大静摩擦力等于滑动摩擦力。(g取10m/s2)求:
(1)导轨与金属棒间动摩擦因数;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度;
(3)若在竖直平面内改变磁感应强度的大小和方向,使金属棒刚好向ac端移动,则所加磁场的磁感应强度最小值和方向?
19.(12分)粒子加速器是借助于不同形态的电场,将带电粒子加速到高能量的电磁装置。粒子加速器可分为直线加速器和圆形加速器等类型。
(1)图1为多级直线加速器示意图。横截面积相同、长度依次增加的金属圆筒沿轴线依次排列,各筒相间地连接到交变电源的A、B两极,两极间电压uAB随时间的变化规律如图2所示。t=0时,序号为0的金属圆板中央一个质量为m、电荷量为+q的粒子,在圆板和圆筒之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。已知交变电源电压的绝对值为U,周期为T,带电粒子的重力和通过圆筒间隙的时间忽略不计。如果带电粒子每次经过圆筒之间都能被加速,求第n个圆筒的长度Ln;
(2)回旋加速器使带电粒子沿近似圆形的轨道运动,改进了直线加速器占地较大的问题。回旋加速器的工作原理如图3所示。半径为R的高真空的D形金属盒处在匀强磁场中,磁感应强度大小为B,方向与盒面垂直。将两盒与电压为U的高频交变电源相连,两盒的狭缝间形成周期性变化的电场。A处粒子源产生的带电粒子,质量为m、电荷量为+q,初速度为0。调整交流电源的频率可使粒子每次通过狭缝时都能被加速。不计带电粒子穿过狭缝的时间和粒子所受重力。求:
①所加交流电的频率f;
②粒子获得的最大动能Ekm。
(3)对于质量较小的电子,由于受到相对论效应的影响,回旋加速器就不适用了。加速电子可以用电子感应加速器。图4是其结构图(上为侧视图,下为真空室俯视图),圆形电磁铁两极间有一环形真空室,在交变电流的激励下,两极间出现交变磁场,交变磁场又激发出感生电场。从电子枪射入真空室的电子在感生电场力和洛伦兹力的共同作用下,在真空室内做加速圆周运动,加速完成后,电子束被引离轨道进入靶室。图5为一周期内磁场的变化情况,B为正时表示B的方向竖直向上。已知电子带负电,试简要分析在一周期内的哪段时间内,电子可被加速做圆周运动?
2021-2022学年北京市密云区高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.多选题(共10小题,满分30分,每小题3分)
1.(3分)如图所示为两点电荷a、b所形成电场的电场线分布图,有一带电粒子仅在电场力的作用下沿虚线运动,先后经过虚线上A、B、C三点,则下列说法正确的是( )
A.带电粒子的加速度大小aA>aB>aC
B.带电粒子的电势能先减小后增大
C.a、b两点电荷的电荷量大小qa<qb
D.三点的电势大小满足φC>φB>φA
【解答】解:A、电场线的疏密表示电场的强弱,由图知EA<EB<EC,由F=qE得:FA<FB<FC,由牛顿第二定律a=得:aA<aB<aC,故A错误;
B、物体做曲线运动时轨迹向合力一侧弯曲,速度沿切线方向,从A到B,电场力对粒子做正功,电势能减小;从B到C,电场力对粒子做负功,电势能增大,故B正确;
C、由轨迹可知a对粒子是引力,b对粒子是斥力,从B到C弯曲程度加大,b对粒子的斥力大于a对粒子的引力,且粒子到a的距离小于到b的距离,由库仑定律可知:
qa<qb,故C正确;
D、由于a、b的电性不确定,无法比较三点的电势高低,故D错误。
故选:BC。
2.(3分)以下所用物理学研究方法的叙述,正确的是( )
A.用质点来代替物体,是建立理想模型法
B.v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是类比法
C.当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法
D.认为空气中由静止开始下落的苹果做自由落体运动,是控制变量法
【解答】解:A、质点采用的科学方法为建立理想化的物理模型法,故A正确;
B、v﹣t图象中图线与坐标轴围成的图形的面积表示位移,是微元法,故B错误;
C、当Δt非常小时,表示物体在t时刻的瞬时速度,是极限法,故C正确;
D、认为空气中由静止开始下落的苹果做自由落体运动,是理想模型法,故D错误;
故选:AC。
3.(3分)如图所示,理想变压器的原线圈接在u=220sin100πt(V)的交流电源上,副线圈接有R=55Ω的负载电阻,原、副线圈匝数之比为2:1,电流表、电压表均为理想电表。下列说法正确的是( )
A.电流表的读数为1.00 A B.电流表的读数为2.00A
C.电压表的读数为110V D.电压表的读数为155V
【解答】解:AB、由瞬时值的表达式可得,原线圈的电压有效值为220V,根据电压与匝数成正比可得,副线圈的电压为110V,再由输入功率和输出功率相等可得220I1=W,所以原线圈的电流的大小为1.00A,电流表读数为1.00A,故A正确,B错误。
CD、电压表的读数为电压的有效值,由A的分析可知,副线圈的有效值为110V,所以电压表的读数为110V,故C正确,D错误。
故选:AC。
4.(3分)如图所示,当磁场的磁感应强度B增强时,则金属环有( )
A.顺时针的感应电流 B.逆时针的感应电流
C.收缩的趋势 D.扩张的趋势
【解答】解:AB、当磁场的磁感应强度B增强时,穿过闭合回路的磁通量向里增加,根据楞次定律,感应电流的磁场方向向外,根据安培定则,感应电流为逆时针方向,故A错误,B正确。
CD、穿过闭合回路的磁通量增加,根据楞次定律,环有收缩的趋势,故C正确,D错误。
故选:BC。
5.(3分)如图电路中,电阻R随温度升高均匀增大,用这个电阻做探头测温,把电流表的刻度改为相应的温度刻度。下列说法正确的是( )
A.低温对应电流较大的刻度上,且温度刻度均匀
B.低温对应电流较大的刻度上,且温度刻度不均匀
C.高温对应电流较大的刻度上,且温度刻度均匀
D.高温对应电流较大的刻度上,且温度刻度不均匀
【解答】解:根据图示电路图结合闭合电路的欧姆定律得:E=I(r+R+RA),
解得电路的电流为:I=,可见电阻R越小,电流I越大,对应的温度越低,所以低温对应电流较大的刻度上;
由于电阻R随温度升高均匀增大,则电阻R与温度的变化为:R=R0+kt(k>0),
解得:t=(RA+r+R0),所以t与I不是线性关系,温度刻度不均匀,故B正确、ACD错误。
故选:B。
6.(3分)智能手机耗电量大,移动充电宝应运而生,它是能直接给移动设备充电的储能装置。充电宝的转化率是指电源放电总量占电源容量的比值,一般在0.60﹣0.70之间(包括移动电源和被充电池的线路板、接头和连线的损耗)。如图为某一款移动充电宝,其参数见如表,下列说法正确的是( )
容量 20000mAh 兼容性 所有智能手机
输入 DC5V2AMAX 输出 DC5V0.1﹣2.5A
尺寸 156*82*22mm 转换率 0.60
产品名称 索扬 重量 约430g
A.给充电宝充电时将大部分电能转化为化学能
B.该充电宝最多能储存能量为20000mAh
C.理论上该充电宝电量从零到完全充满电的时间约为10h
D.该充电宝给电量为零、容量为3000mAh的手机充电,则理论上能充满4次
【解答】解:A、给充电宝充电时是把电能转化为化学能的过程,故A正确;
B、该充电宝的容量为:q=20000mAh=20000×10﹣3×3600=7.2×104C,
该电池的电动势为5V,所以充电宝储存的能量:E=E电动势 q=5×7.2×104=3.6×105J;故B错误;
C、该充电宝的容量为:q=20000mAh=2000×10﹣3×3600=7.2×104C
以2A的电流为用电器供电则供电时间t==10h,故C正确。
D、由于充电宝的转化率是0.6,所以可以释放的电能为:20000mA h×0.6=12000mAh,给容量为3000mAh的手机充电的次数:n=4,故D正确。
故选:ACD。
7.(3分)如图所示,一个带电粒子从y轴上的a点沿xOy平面且与y轴成45°角的方向进入xOy平面内,粒子经过垂直于xOy平面的圆形匀强磁场区域后从x轴上的b点射出,射出方向与x轴成75°角。已知带电粒子的质量为m、电荷量为q,带电粒子的运动速率为v,磁场的磁感应强度大小为B,不计粒子的重力,则下列说法正确的是( )
A.粒子在磁场中运动的时间为
B.粒子在磁场中运动的时间为
C.圆形磁场区域的最小半径为
D.圆形磁场区域的最小半径为
【解答】解:AB、根据几何知识知速度偏转角为:θ=45°+75°=120°
粒子在磁场中的周期为:T=
所以粒子在磁场中运动的时间为:t==,故A正确,B错误;
CD、连接ab为圆周运动的弦,根据几何知识知磁场最小半径为:R=ab=rsin60°==,故C正确,D错误。
故选:AC。
8.(3分)电源、开关、滑动变阻器和平行板电容器连成如图所示电路,P点到A、B两极板的距离相等,且B板接地。闭合开关S,电源对电容器充电后,电容器带电荷量为Q,板间电压为U,板间电场强度大小为E。则下列说法正确的是( )
A.若将A板下移少许,则Q变大,U不变,E变大
B.若滑动变阻器的滑片向左移动,则Q变大,U减小,E变大
C.若断开开关,将A板下移少许,则P点的电势不变
D.若断开开关,将A板向左移动少许,则Q不变,U不变,E不变
【解答】解:A、保持开关闭合,则极板间电压U不变,若将A板下移少许,即减小极板间距d,由C= 可知,电容器的电容增大;由Q=UC可知,Q增大,由E0= 可知,电场强度变大,故A正确;
B、因滑动变阻器与电容器串联接在电源上,其变阻器相当于导线,则滑片的移动不会改变电路电压,则Q、U及E均不变,故B错误;
CD、给电容器充电后与电源断开,电量Q不变,若将A板下移少许,即减小极板间距,由C= 可知,电容器的电容增大;由Q=UC可知,U减小,由E0== 可知,E0不变,所以P点到下极板的电压不变,则P点的电势也不变,故C正确,D错误。
故选:AC。
9.(3分)如图所示,电源的电动势为E,内阻为r。A、B是两个相同的小灯泡,L是一个自感系数相当大的线圈,其直流电阻不能忽略。关于这个电路的以下说法正确的是( )
A.开关闭合后,A灯立刻亮
B.开关闭合后,B灯立刻亮,而后逐渐变暗,最后亮度稳定
C.开关断开后瞬间,A灯左端电势比右端电势低
D.开关断开后瞬间,A灯闪亮一下再熄灭,B灯立即熄灭
【解答】解:A、开关闭合到瞬间电压直接加到灯泡A上,所以开关闭合到电路中电流稳定的时间内,A灯立刻亮,故A正确;
B、开关闭合到电路中电流稳定的时间内,线圈开始时产生自感电动势,自感电动势随对电流阻碍较小后B灯逐渐变亮,当线圈对电流没有阻碍时,灯泡B亮度稳定,故B错误;
C、开关处于闭合状态,在断开瞬间,线圈相当于电源,电流方向仍不变,所以电流自右向左通过A灯,A灯左端电势比右端电势低,故C正确;
D、开关处于闭合状态,在断开瞬间,线圈与两个灯泡组成自感回路,由于两灯泡完全一样,所以不会出现电流比之前还大的现象,因此A灯不会闪亮一下,只会与B一起慢慢熄灭,故D错误;
故选:AC。
10.(3分)如图所示,静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线。一个带负电的粒子在电场中以x=0为中心,沿x轴方向在区间[﹣A,A]之间做周期性运动,A<d.若φ0、d、A为已知量,且已知该粒子的比荷为.利用这些数据结合图象可以得出( )
A.该电场为匀强电场,且电场强度大小为
B.粒子运动时的加速度大小为
C.在x=0处粒子速度最大,为
D.粒子做周期性运动,且运动周期为
【解答】解:A、由图可知,0与d(或﹣d)两点间的电势差为φ0,电势随x均匀变化,电场为匀强电场,则电场强度的大小为:E=,故A正确。
B、粒子所受的电场力的大小为F=qE,由牛顿第二定律得:加速度为a==,故B错误;
C、粒子经过x=0时速度最大,设其大小为v,从A到O过程,由动能定理得:
qEA=mv2
解得:v==,故C正确。
D、粒子从x=0处开始运动的四分之一周期内做匀加速直线运动,用时t=,粒子完成一次往复运动的时间为 T=4t,运动周期为T=4,故D正确。
故选:ACD。
二.填空题(共2小题,满分15分)
11.(3分)一只电流表表头G的满偏电流为Ig=3mA,内阻为Rg=100Ω。若改装成量程为I=300mA的电流表,则改装后的电流表内阻为 1 Ω;若改装成量程为U=15V的电压表,则改装后的电压表内阻为 5000 Ω。
【解答】解:改装成电流表时需要并联小电阻,改装后电压等于电流表的满偏电压Ug=0.003×100V=0.3V;总电流I=300mA=0.3A;由欧姆定律可得,改装后电流表内阻R1==Ω=1Ω;
改装成电压表时需要串联大电阻,电路中电流为满偏电流Ig=3mA=0.003A,此时串联部分电压U=15V,由欧姆定律可得,R==Ω=5000Ω。
故答案为:1;5000。
12.(12分)某实验小组利用如图甲所示的电路图测定一电源的电动势(大约为6V)和内电阻。要求尽量减小实验误差。
(1)在下列两个电压表中选择一个最合适的来改装成量程为0~9V的电压表。
①量程为0~2V、内阻为2kΩ的电压表
②量程为0~3V、内阻为3kΩ的电压表
则应选择电压表 ② ,且串联一个阻值为 6 kΩ的电阻,就可以改装成量程为0~9V的电压表。
(2)现有电流表(0~0.6A),开关和导线若干,以及以下器材:
A.滑动变阻器R1(0~50Ω)
B.滑动变阻器R2(0~500Ω)
实验中滑动变阻器应选用 A (填相应器材前的代号)。
(3)某位同学记录的6组数据如表所示,其中5组数据的对应点已经标在图乙的坐标纸上,请标出余下一组数据的对应点,并在坐标纸上正确作出U﹣I图线。
序号 1 2 3 4 5 6
电压U(V) 5.80 5.60 5.20 5.00 4.80 4.40
电流I(A) 0.060 0.120 0.240 0.260 0.360 0.480
(4)根据(3)中所画图线,可得出该电源的电动势E= 6.0 V,内电阻r= 3.3 Ω(结果均保留两位有效数字)。
(5)本次实验中,由于系统误差导致所测得的电源电动势 偏小 (填“偏大”“偏小”或”不变”)。
内阻 偏小 (填“偏大”“偏小”或“不变”)。
【解答】解:(1)应选择量程为0~3V、内阻为3kΩ的电压表②进行改装,改装后量程与内阻都扩大3倍,根据串联电路特点可知,串联分压电阻阻值为原电表内阻的2倍,串联电阻阻值为6kΩ。
(2)电源电动势约为6V,电流表量程为0.6A,电路最小电阻约为R=Ω=10Ω,为方便实验操作,滑动变阻器应选择A。
(3)根据表中实验数据在坐标系内描出对应点,让尽可能多的点过直线,不能过直线的点对称分布在直线两侧,偏离直线太远的点应舍去,根据坐标系内描出的点作出图象如图所示;
(4)由图甲所示可知,路端电压U=E﹣Ir,由图示电源UI图象可知,电源电动势E=6.0V,内阻r=Ω≈3.3Ω。
(5)由图甲所示电路图可知,当外电路短路时,电流的测量值等于真实值,除此之外,由于电压表的分流作用,电流的测量值小于真实值,电源的U﹣I图象如图所示,由图象可知,电源电动势的测量值小于真实值,电源内阻测量值小于真实值.
故答案为:(1)②;6;(2)A;(3)图象如图所示;(4)6.0;3.3;(5)偏小;偏小。
三.计算题(共7小题,满分65分)
13.(8分)如图所示,在水平面上固定有两平行长直导轨,右端接一电阻R═1.2Ω导轨内有一方向竖直向上、磁感应强度大小B=0.5T的匀强磁场。磁场区域为曲线方程y=sin(x)(x、y的单位均为m)与x轴所围的空间,其中0≤x≤4m,一电阻r=0.3Ω、长度L=1.2m的金属棒ab垂直搁在导轨上并在水平拉力作用下从x=0处以速度v=3m/s沿x轴正方向做匀速直线运动。导轨电阻不计,取g=10m/s2,求:
(1)ab两端电压的最大值Um;
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q。
【解答】解:(1)金属棒ab切割感线最大的长度为 ym=1.0m
金属棒ab中产生的感应电动势的最大值为 Em=Bymv
根据闭合电路欧姆定律有 Im=
ab两端电压的最大值为 Um=ImR
联立解得 Um=1.2V
(2)金属棒ab在磁场中切割磁感线产生的感应电动势瞬时值为:e=Byv
上式中 y=sin(x)(m),其中 x=vt
解得 e=1.5sint(V)
可知感应电动势的最大值为 Em=1.5V
有效值为 E=
金属棒ab在磁场中运动的时间为 t=,其中 x0=4m
这段时间内回路中产生的总焦耳热为 Q=t
解得 Q=1J
答:(1)ab两端电压的最大值Um是1.2V。
(2)金属棒通过磁场的过程中,回路中产生的总焦耳热Q是1J。
14.(8分)氢原子由一个质子(原子核)和一个核外电子组成。电子质量me=9.1×10﹣31kg,质子质量mp=1.67×10﹣27kg,电子和原子核所带电荷量都等于e=1.6×10﹣19C。电子绕核旋转的轨道半径r=5.3×10﹣11m。试求:电子所受静电引力是万有引力的多少倍?
【解答】解:根据仑定律得库仑力大小:
F电=k=8.2×10﹣8N
根据万有引力定律得万有引力大小:
F万=G=3.6×10﹣47N,
所以
=2.28×1039。
答:电子所受静电引力是万有引力的2.28×1039倍。
15.(8分)如图所示,长为L=1m的平行金属板水平放置,两极板带等量的异种电荷,板间形成竖直方向的匀强电场,一个质量为m=4×10﹣3kg,电量为q=2×10﹣6C的带负电荷的粒子,以初速度v0=4m/s紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时速度恰与入射方向成37°,不计粒子重力,sin37°=0.6,cos37°=0.8。求:
(1)粒子射出下极板边缘时的动能;
(2)匀强电场的场强E的大小和方向。
【解答】解:(1)粒子离开电场时,合速度与水平夹角为37°,如图所示
粒子射出下极板边缘时速度大小为:
射出电场时动能为:Ek=
两式联立解得:;
(2)粒子在匀强电场中做类平抛运动
水平方向:L=v0t
竖直方向:vy=at=t
又有:
解得:
代入数据得:E=2.4×104V/m
根据已知条件粒子所受电场力竖直向下,又因为粒子带负点,负电荷受力的方向与场强的方向相反,故匀强电场的方向竖直向上。
答:(1)粒子射出下极板边缘时的动能为5×10﹣2J;
(2)匀强电场的场强E的大小为2.4×104V/m,方向竖直向上。
16.(9分)间距为L的两平行光滑金属导轨如图所示,x轴平行导轨,y轴垂直导轨。在x=﹣x1位置有一宽度可不计的绝缘薄层,隔开左右两部分电路。在导轨间存在磁场,y轴左侧磁场方向垂直纸面向外,y轴右侧磁场方向垂直纸面向里,x<﹣x1区域磁场恒为B0,﹣x1≤x≤x0区域磁感应强度沿y轴方向磁感应强度大小不变,沿x轴方向磁感应强度大小随x变化,而且变化规律相同,在x=x0处磁感应强度大小为B0.导轨右侧的恒流源在开关S接通时为电路提供恒定的电流I(方向如图中箭头所示);导轨左侧接一阻值为R的电阻。有阻值为R的金属棒ab垂直导轨静止于x0处,当开关S接通时发现其在y轴右侧的位移随时间的变化规律为x=x0cosωt,其中为ω为已知常数,且2|﹣x1|=x0。
(1)金属棒ab的质量m为多少;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为多少。
【解答】解:(1)对x=x0cosωt求导有:v=﹣ωx0sinωt,
再对v求导得:
当t=0时:
故得 ;
(2)由x0→x1过程:
流过金属棒ab的电量
由x1到最左端:
又根据动量定理得
﹣B0lt2=0﹣mv1
又 t2=qt2
则得﹣B0q2l=0﹣mv1
故 ;
因此,金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量 ;
(3)由x0→﹣x1过程:
﹣x1到最左边过程:
则。
答:(1)金属棒ab的质量m为得 ;
(2)金属棒ab从x=﹣x1运动至最左边的过程中流过金属棒ab的电量为 ;
(3)金属棒ab从x=x0运动至最左边的过程金属棒ab产生的焦耳热Q为。
17.(10分)如图所示,足够长的平行光滑金属导轨固定在水平面上,间距为L,一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场,磁感应强度为B.电阻为r的导体棒MN放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的恒力F作用下,导体棒沿导轨向右匀速运动,速度大小为v。
(1)求导体棒两端的电压;
(2)通过公式推导验证:在△t时间内,恒力F所做的功W等于电路获得的电能W电,也等于电路中产生的焦耳热Q;
(3)从微观角度看,导体棒MN中的自由电荷会同时参与沿导体棒方向和垂直导体棒方向的两个分运动,由此会受到两个相应的洛伦兹力,请你通过计算证明:导体棒中一个自由电荷所受的洛伦兹力做的总功为零。(为了方便,可认为导体棒中的自由电荷为正电荷。)
【解答】解:(1)导体棒沿导轨向右匀速运动产生感应电动势E = BLv
由闭合电路欧姆定律可得,电路中电流I=
导体棒两端电压U=IR=;
(2)导体棒匀速运动,受力平衡F=FA=BIL
在△t时间内,
恒力F做功W=Fv△t=FAv△t=BILv△t=
电路获得的电能W电=qE=EI△t=
电路中产生的焦耳热Q=I2(R+r)△t=
可见,恒力F所做的功等于电路获得的电能W电,也等于电路中产生的焦耳热Q。
(3)设自由电荷的电荷量为q,沿导体棒定向移动的速率为u。
沿导体棒方向的洛伦兹力f1=qvB
在△t时间内,f1做正功Q1=f1u△t=qvBu△t
垂直导体棒方向的洛伦兹力f2=qvB
在△t时间内,f2做负功W2=﹣f2 u△t=﹣quBv△t
所以W1+W2=0,即导体棒中一个自由电荷所受的洛伦兹力做的总功为零。
答:(1)导体棒两端的电压为;
(2)推导过程见解析;
(3)证明见解析。
18.(10分)如图所示,在同一水平面的两导轨相互平行,相距2m并处于竖直向上的磁感应强度为B=0.75T的匀强磁场中,一根质量为1kg的金属棒放在导轨上且与导轨垂直。当金属棒中通如图所示的电流为5A时,金属棒恰好做匀速直线运动,最大静摩擦力等于滑动摩擦力。(g取10m/s2)求:
(1)导轨与金属棒间动摩擦因数;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度;
(3)若在竖直平面内改变磁感应强度的大小和方向,使金属棒刚好向ac端移动,则所加磁场的磁感应强度最小值和方向?
【解答】解:(1)金属棒受到的安培力:F=BIL,
由平衡条件得:μmg=BIL,
代入数据得:μ=0.75;
(2)金属棒受到的安培力:F′=BI′L,
由牛顿第二定律得:BI′L﹣μmg=ma,
代入数据得:a=6m/s2;
(3)金属棒刚好向ac端移动且磁感应强度最小时,
由平衡条件得:B′IL=mg,
代入数据得:B′=1T,
根据左手定则可知,磁感应强度方向水平向左;
答:(1)导轨与金属棒间动摩擦因数为0.75;
(2)若只改变电流的大小,使电流增加到9A时,金属棒将获得多大的加速度6m/s2;
(3)所加磁场的磁感应强度最小值为1T,方向:水平向左。
19.(12分)粒子加速器是借助于不同形态的电场,将带电粒子加速到高能量的电磁装置。粒子加速器可分为直线加速器和圆形加速器等类型。
(1)图1为多级直线加速器示意图。横截面积相同、长度依次增加的金属圆筒沿轴线依次排列,各筒相间地连接到交变电源的A、B两极,两极间电压uAB随时间的变化规律如图2所示。t=0时,序号为0的金属圆板中央一个质量为m、电荷量为+q的粒子,在圆板和圆筒之间的电场中由静止开始加速,沿中心轴线冲进圆筒1。已知交变电源电压的绝对值为U,周期为T,带电粒子的重力和通过圆筒间隙的时间忽略不计。如果带电粒子每次经过圆筒之间都能被加速,求第n个圆筒的长度Ln;
(2)回旋加速器使带电粒子沿近似圆形的轨道运动,改进了直线加速器占地较大的问题。回旋加速器的工作原理如图3所示。半径为R的高真空的D形金属盒处在匀强磁场中,磁感应强度大小为B,方向与盒面垂直。将两盒与电压为U的高频交变电源相连,两盒的狭缝间形成周期性变化的电场。A处粒子源产生的带电粒子,质量为m、电荷量为+q,初速度为0。调整交流电源的频率可使粒子每次通过狭缝时都能被加速。不计带电粒子穿过狭缝的时间和粒子所受重力。求:
①所加交流电的频率f;
②粒子获得的最大动能Ekm。
(3)对于质量较小的电子,由于受到相对论效应的影响,回旋加速器就不适用了。加速电子可以用电子感应加速器。图4是其结构图(上为侧视图,下为真空室俯视图),圆形电磁铁两极间有一环形真空室,在交变电流的激励下,两极间出现交变磁场,交变磁场又激发出感生电场。从电子枪射入真空室的电子在感生电场力和洛伦兹力的共同作用下,在真空室内做加速圆周运动,加速完成后,电子束被引离轨道进入靶室。图5为一周期内磁场的变化情况,B为正时表示B的方向竖直向上。已知电子带负电,试简要分析在一周期内的哪段时间内,电子可被加速做圆周运动?
【解答】解:(1)设带电粒子进入第n个圆筒时的速度为vn,根据动能定理有:nqU=
如果粒子匀速穿过每个圆筒的时间恰好等于交变电压周期的一半,那它每到达一个间隙都能被加速,有:Ln=vn×
解得:Ln=;
(2)①如果交变电源的频率等于粒子圆周运动的频率,那么粒子每次通过狭缝时都能被加速。
根据洛伦兹力提供向心力可得:qvB=m
交变电流的频率f==
解得:f=;
②粒子的速度与半径成正比,所以当圆周运动的半径最大时,粒子的动能最大。
根据洛伦兹力提供向心力可得:qvmB=m
解得:Ekm==;
(3)在第一个时间内,电子可被加速做圆周运动。
由楞次定律可知,在第一个和第四个时间内,感生电场的方向为顺时针方向,电子受力方向为逆时针方向,可被加速;
由左手定则可知,只有磁场方向向上时,电子所受洛伦兹力才指向圆心,充当向心力。
综合考虑,只有第一个时间内,电子可被加速做圆周运动。
答:(1)第n个圆筒的长度为;
(2)①所加交流电的频率为;
②粒子获得的最大动能为;
(3)只有第一个时间内,电子可被加速做圆周运动。
同课章节目录
