沪科版八下数学 19.3矩形、菱形、正方形 矩形的判定 课件(共16张)
文档属性
| 名称 | 沪科版八下数学 19.3矩形、菱形、正方形 矩形的判定 课件(共16张) |  | |
| 格式 | pptx | ||
| 文件大小 | 431.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 13:51:02 | ||
图片预览




文档简介
(共16张PPT)
沪科版数学八年级下
19.3 矩形的判定
沪科版数学八年级下
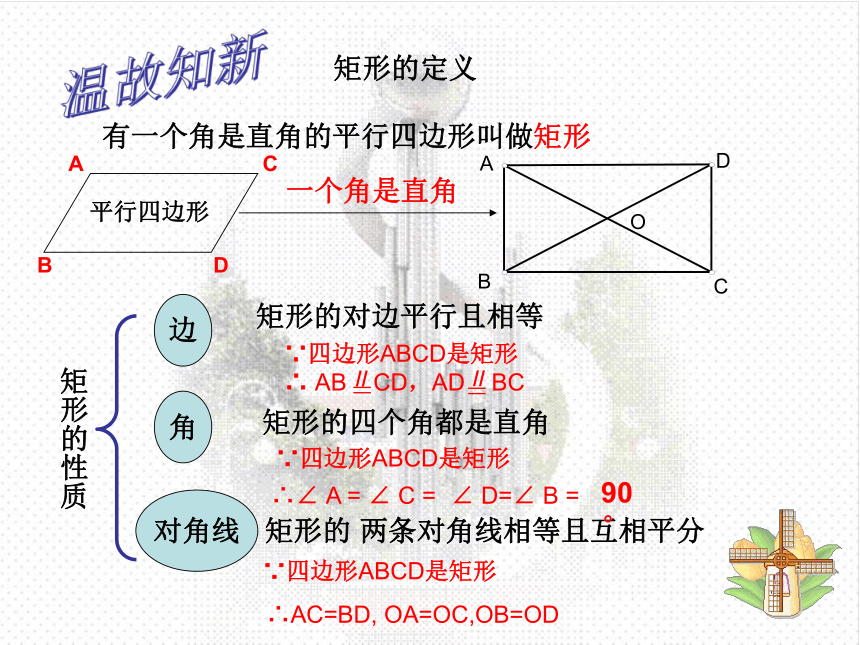
有一个角是直角的平行四边形叫做矩形
矩形的 两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
矩形的定义
边
对角线
角
矩形的性质
平行四边形
A
B
C
D
一个角是直角
//
∵四边形ABCD是矩形
∴ AB CD,AD BC
//
=
=
∵四边形ABCD是矩形
∴AC=BD, OA=OC,OB=OD
90°
∴∠ A = ∠ C =
∠ D=∠ B =
∵四边形ABCD是矩形
温故知新
你知道如何判定一个平行四边形是矩形吗?
矩形判定1
(定义):
有一个角是直角的平行四边形是矩形。
几何语言:
你还有其它的判定方法吗?
四边形ABCD是矩形
∴
∠A=900
∵
(矩形的定义)
平行四边形,
四边形ABCD是
请你思考
交流:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
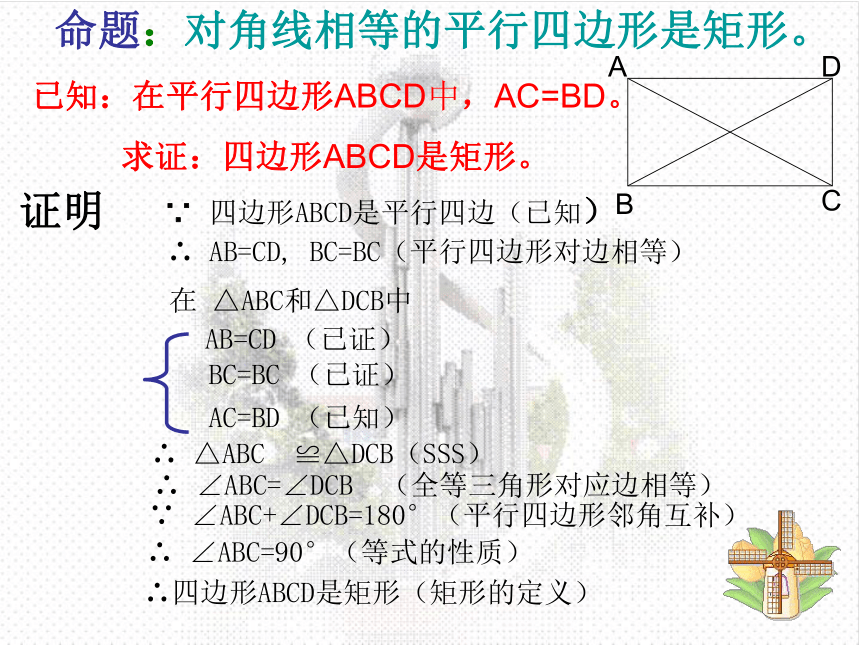
命题:对角线相等的平行四边形是矩形。
证明
已知:在平行四边形ABCD中,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
∵ 四边形ABCD是平行四边(已知)
∴ AB=CD, BC=BC(平行四边形对边相等)
在 △ABC和△DCB中
AB=CD (已证)
BC=BC (已证)
AC=BD (已知)
∴ △ABC ≌△DCB(SSS)
∵ ∠ABC+∠DCB=180°(平行四边形邻角互补)
∴ ∠ABC=90°(等式的性质)
∴四边形ABCD是矩形(矩形的定义)
∴ ∠ABC=∠DCB (全等三角形对应边相等)
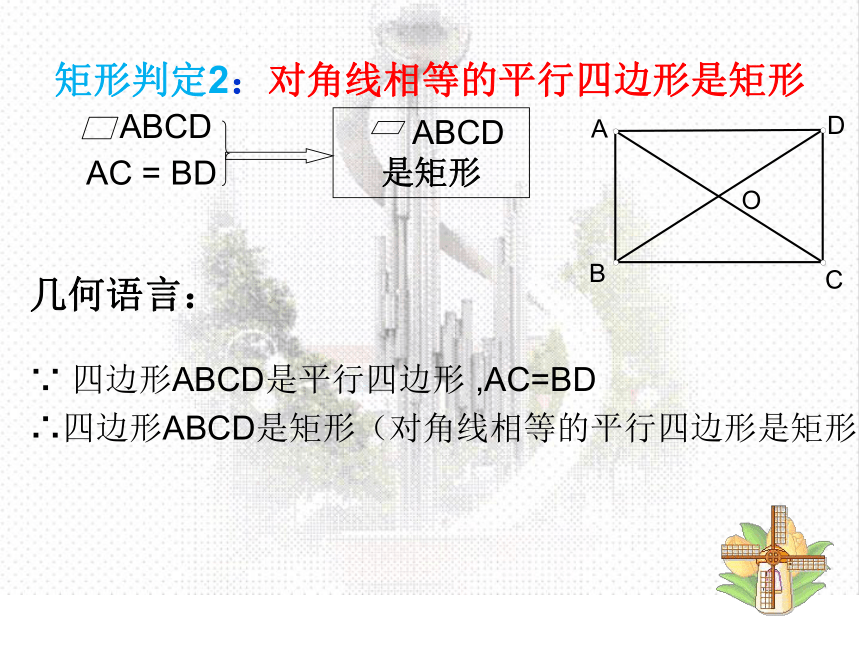
矩形判定2:对角线相等的平行四边形是矩形
ABCD
AC = BD
ABCD
是矩形
几何语言:
∵ 四边形ABCD是平行四边形 ,AC=BD
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形 )
如果想从角的方向判断一个四边形是矩形 ,试想一想:需要角满足什么条件?
能证明它的正确性吗
命题:
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
求证:四边形ABCD是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
D
B
C
A
∴四边形ABCD是矩形.
有三个角是直角的四边形是矩形
矩形判定3:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
D
B
C
A
几何语言:
∵
∠A= ∠B= ∠C=90°
∴四边形ABCD是矩形
(有三个角是直角的四边形是矩形)
1.一个角是直角的平行四边形是矩形
2.对角线相等的平行四边形是矩形
3.三个角是直角是四边形是矩形
归纳:
矩形的三种判定方法
探究:
判定1:
有一个角是直角的平行四边形是矩形
判定2:
对角线相等的平行四边形是矩形
有一个角是直角且两组对边分别平行的四边形是矩形
有一个角是直角且两组对边分别相等的四边形是矩形
有一个角是直角且一组对边平行且相等的四边形是矩形
有一个角是直角且对角线互相平分的四边形是矩形
对角线相等且两组对边分别平行的四边形是矩形
对角线相等且两组对边分别相等的四边形是矩形
对角线相等且一组对边平行且相等的四边形是矩形
对角线相等且对角线互相平分的四边形是矩形
课堂练习:
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
D
D
一.选择题
二.判断题
对角线相等的四边形是矩形。
对角线互相平分且相等的四边形是矩形。
有一个角是直角的四边形是矩形。
四个角都是直角的四边形是矩形。
四个角都相等的四边形是矩形。
对角线相等且有一个角是直角的四边形是矩形。
对角线相等且互相垂直的四边形是矩形。
例1、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,
求证:四边形AEBD是矩形。
A
B
C
D
E
P
1
2
证明:
∵BD,BE分别是∠ABC,∠ABP的平分线
∴∠1=1/2 ∠ABC,∠2=1/2 ∠ABP
∵∠ABC+∠ABP=180°.
∴∠1+∠2=1/2∠ABC+1/2∠ABP).
=1/2(∠ABC+∠ABP)
=1/2×180°
=90°
∴∠EBD=90°
∵AE⊥BE,AD⊥BD
∴∠AEB=∠ADB=90°
∴四边形AEBD是矩形
(有三个角是直角的四边形是矩形)
1.一个角是直角的平行四边形是矩形
2.三个角是直角是四边形是矩形
3.对角线相等的平行四边形是矩形
矩形的三种判定方法
我的收获
再见
沪科版数学八年级下
19.3 矩形的判定
沪科版数学八年级下
有一个角是直角的平行四边形叫做矩形
矩形的 两条对角线相等且互相平分
矩形的对边平行且相等
矩形的四个角都是直角
矩形的定义
边
对角线
角
矩形的性质
平行四边形
A
B
C
D
一个角是直角
//
∵四边形ABCD是矩形
∴ AB CD,AD BC
//
=
=
∵四边形ABCD是矩形
∴AC=BD, OA=OC,OB=OD
90°
∴∠ A = ∠ C =
∠ D=∠ B =
∵四边形ABCD是矩形
温故知新
你知道如何判定一个平行四边形是矩形吗?
矩形判定1
(定义):
有一个角是直角的平行四边形是矩形。
几何语言:
你还有其它的判定方法吗?
四边形ABCD是矩形
∴
∠A=900
∵
(矩形的定义)
平行四边形,
四边形ABCD是
请你思考
交流:工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:
对角线相等的平行四边形是矩形 。
命题:对角线相等的平行四边形是矩形。
证明
已知:在平行四边形ABCD中,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
∵ 四边形ABCD是平行四边(已知)
∴ AB=CD, BC=BC(平行四边形对边相等)
在 △ABC和△DCB中
AB=CD (已证)
BC=BC (已证)
AC=BD (已知)
∴ △ABC ≌△DCB(SSS)
∵ ∠ABC+∠DCB=180°(平行四边形邻角互补)
∴ ∠ABC=90°(等式的性质)
∴四边形ABCD是矩形(矩形的定义)
∴ ∠ABC=∠DCB (全等三角形对应边相等)
矩形判定2:对角线相等的平行四边形是矩形
ABCD
AC = BD
ABCD
是矩形
几何语言:
∵ 四边形ABCD是平行四边形 ,AC=BD
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形 )
如果想从角的方向判断一个四边形是矩形 ,试想一想:需要角满足什么条件?
能证明它的正确性吗
命题:
证明:
∵ ∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
∴四边形ABCD是平行四边形.
求证:四边形ABCD是矩形.
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
D
B
C
A
∴四边形ABCD是矩形.
有三个角是直角的四边形是矩形
矩形判定3:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD
是矩形
D
B
C
A
几何语言:
∵
∠A= ∠B= ∠C=90°
∴四边形ABCD是矩形
(有三个角是直角的四边形是矩形)
1.一个角是直角的平行四边形是矩形
2.对角线相等的平行四边形是矩形
3.三个角是直角是四边形是矩形
归纳:
矩形的三种判定方法
探究:
判定1:
有一个角是直角的平行四边形是矩形
判定2:
对角线相等的平行四边形是矩形
有一个角是直角且两组对边分别平行的四边形是矩形
有一个角是直角且两组对边分别相等的四边形是矩形
有一个角是直角且一组对边平行且相等的四边形是矩形
有一个角是直角且对角线互相平分的四边形是矩形
对角线相等且两组对边分别平行的四边形是矩形
对角线相等且两组对边分别相等的四边形是矩形
对角线相等且一组对边平行且相等的四边形是矩形
对角线相等且对角线互相平分的四边形是矩形
课堂练习:
(1)矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等(C)对边平行且相等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等(C)是轴对称图形(D)对角线垂直
D
D
一.选择题
二.判断题
对角线相等的四边形是矩形。
对角线互相平分且相等的四边形是矩形。
有一个角是直角的四边形是矩形。
四个角都是直角的四边形是矩形。
四个角都相等的四边形是矩形。
对角线相等且有一个角是直角的四边形是矩形。
对角线相等且互相垂直的四边形是矩形。
例1、BD、BE分别是∠ABC与它的邻补角的平分线,AE⊥BE,AD⊥BD,
求证:四边形AEBD是矩形。
A
B
C
D
E
P
1
2
证明:
∵BD,BE分别是∠ABC,∠ABP的平分线
∴∠1=1/2 ∠ABC,∠2=1/2 ∠ABP
∵∠ABC+∠ABP=180°.
∴∠1+∠2=1/2∠ABC+1/2∠ABP).
=1/2(∠ABC+∠ABP)
=1/2×180°
=90°
∴∠EBD=90°
∵AE⊥BE,AD⊥BD
∴∠AEB=∠ADB=90°
∴四边形AEBD是矩形
(有三个角是直角的四边形是矩形)
1.一个角是直角的平行四边形是矩形
2.三个角是直角是四边形是矩形
3.对角线相等的平行四边形是矩形
矩形的三种判定方法
我的收获
再见
