沪科版八下数学20.2.2中位数和众数 课件(共19张ppt)
文档属性
| 名称 | 沪科版八下数学20.2.2中位数和众数 课件(共19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 11:56:54 | ||
图片预览




文档简介
沪科版八年级下册
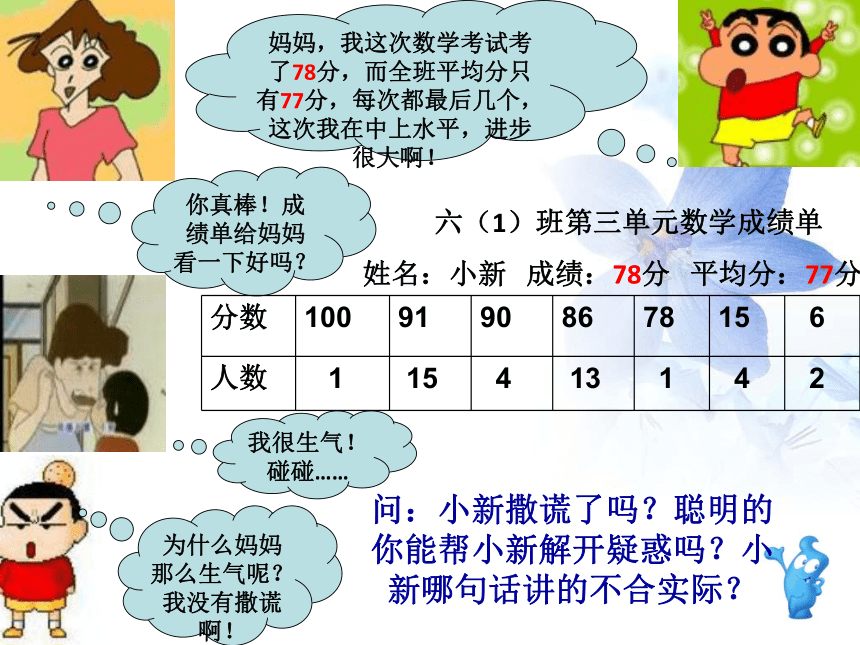
妈妈,我这次数学考试考了78分,而全班平均分只有77分,每次都最后几个,这次我在中上水平,进步很大啊!
你真棒!成绩单给妈妈看一下好吗?
我很生气!碰碰……
分数
100
91
90
86
78
15
6
人数
1
15
4
13
1
4
2
六(1)班第三单元数学成绩单
姓名:小新 成绩:78分 平均分:77分
为什么妈妈那么生气呢?我没有撒谎啊!
问:小新撒谎了吗?聪明的你能帮小新解开疑惑吗?小新哪句话讲的不合实际?
王刚
招聘会现场
我在找工作时,遇到了一件事,请同学们帮我解决一下。
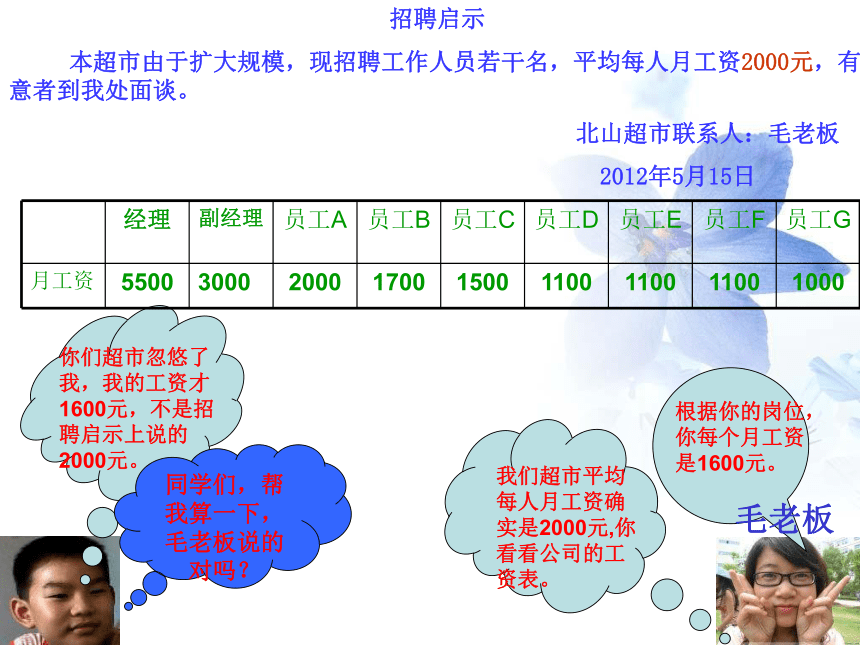
招聘启示
本超市由于扩大规模,现招聘工作人员若干名,平均每人月工资2000元,有意者到我处面谈。
北山超市联系人:毛老板
2012年5月15日
你们超市忽悠了我,我的工资才1600元,不是招聘启示上说的2000元。
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
根据你的岗位,你每个月工资是1600元。
我们超市平均每人月工资确实是2000元,你看看公司的工资表。
毛老板
同学们,帮我算一下,毛老板说的对吗?
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
平均每人月工资
(5500+3000+2000+1700+1500+1100+1100+1100+1000)÷9
=18000÷9
=2000(元)
1、有多少人的工资超过了平均月工资?有多少人的工资低于了平均月工资?
2、是哪几个人的工资影响了平均月工资?
3、用平均数2000元能代表这一组数据准确吗?
平均数可以反映一组数据的整体水平,但是它容易受极端数据的影响。
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
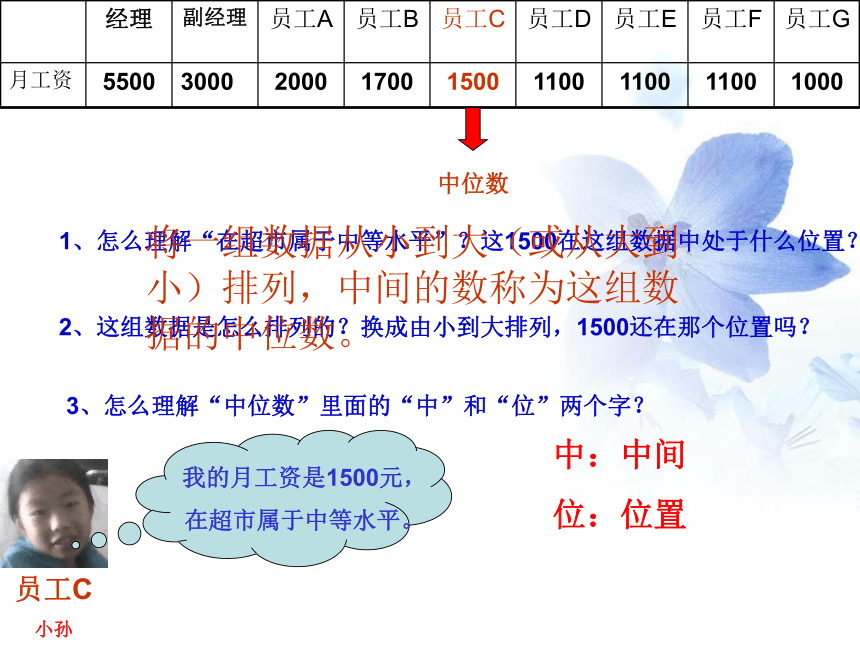
员工C
小孙
我的月工资是1500元,
在超市属于中等水平。
1、怎么理解“在超市属于中等水平”?这1500在这组数据中处于什么位置?
2、这组数据是怎么排列的?换成由小到大排列,1500还在那个位置吗?
中位数
3、怎么理解“中位数”里面的“中”和“位”两个字?
将一组数据从小到大(或从大到小)排列,中间的数称为这组数据的中位数。
中:中间
位:位置
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
王刚
1600
刚才有9个数据,中位数在正中间。现在有十个数据,怎样求它们的中位数呢?请同学们自己试一试。
第一步,重新按顺序排列。
5500 3000 2000 1700 1600 1500 1100 1100 1100 1000
第二步,找正中间的两个数,求它们两个数的平均数。
(1600+1500)÷2
=3100 ÷2
=1550(元)
怎样求一组数据的中位数?
将一组数据由小到大或者由大到小排列。
(1)如果数据个数是奇数,则处于中间位置的数为这组数据的中位数。
(2)如果数据个数是偶数,则中间两个数据的平均数为这组数据的中位数。
比一比,看谁能快速找到我。
题号
数据
中位数
(1)
5 6 2 3 2
(2)
3 7 6 8 8 40 10
(3)
5 6 2 4 3 5
(4)
10 6 12 44 200 55 20 100
3
8
4.5
32
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
我们这里好几个人月工资都是1100元。
员工D
小骆
1、在这组数据中,1100有什么特点?
众数
一组数据中出现次数最多的数称为这组数据的众数。
2、怎么理解众数中“众”的意思?
众:多
下面各组数数据中有众数吗?如果有,找一找。
题号
数据
众数
(1)
40 50 65 33 50 70 50
(2)
3 2 6 7 6 5 3 3 6
(3)
3 0 1 5 9 14
(4)
2 3 5 5 3 2
50
3和6
没有
没有
观察这几组数,你知道了关于众数个数的哪些知识?
1、在一组数据中,可能不止一个众数。
2、在一组数据中,如果每个数据出现的次数相同,这组数据就没有众数。
平均数、中位数、众数是从不同的角度来描述一组数据。
下面不同情况,应该关注哪种数呢?
1、一次考试后,老师想了解全班整体水平怎么样,要关注全班分数的( )。
2、老师想了解全班哪个分数的人最多,要关注全班分数的( )。
3、一个学生想了解自己在全班处于中上还是中下水平,要关注全班分数的( )。
平均数
众数
中位数
比较三个统计量:
区别:三个统计量从不同的侧面提供了一组数据的面貌.
1、平均数:应用范围最广泛,比较可靠和稳定。它与这组数据中的每一个数据都有关系,能够最为充分地反映这组数据所包含的信息,在进行统计推断时有重要的作用。但容易受到极端数据的影响。
2、中位数:在一组数据的数值排序中处于中间位置,在统计 学分析中扮演“分水岭”的角色,人们通过中位数可以对事物大体趋势进行判断和掌控。
3、众数:着眼于各个数据出现次数多少的考察,其大小仅仅与一组数据的部分数据有关系。它反映一组数据的集中水平。
联系:三个统计量都可代表一组数据,表示数据的“平均水平,中等水平或多数水平”,都反映数据的集中趋势。
求出这组数的平均数、中位数和众数。
10 15 5 8 10 10 10 12
平均数是( )
中位数是( )
众数是( )
在一组数据中,有时平均数、中位数和众数可能相同。
10
10
10
在运动会进行跳绳比赛时,我班第一组九个女生1分钟时间跳的次数如下:
234 133 128 92 113 116 182 125 92
(1)分别计算这组数据的平均数和中位数。
(2)你认为平均数、中位数哪一个能更好地表示这组同学的跳绳水平?
中位数能更好地表示这组同学的跳绳水平。因为在一组数据中,有数据偏大或者偏小时,用中位数来代表这组数据的一般水平比平均数更合适。
平均数:(234+133+128+92+113+116+182+125+92 )÷9=135
中位数:234 182 133 128 125 116 113 92 92
中位数是125
在运动会中,五年级女子跳远预决赛成绩如下:
郑芳圆:3.6米 宋 敏 :3.2 米 刘炎炎:3.2米
杜 桦 :3.0米 张守宇:2.6米 崔咏琪:3.0米
根据这组数据,你能提哪些问题?
老师的问题:
(1)在这组数据中,平均数是多少?中位数是多少?众数是多少?
(2)崔咏琪在这6人中处于什么水平?
在运动会集体项目广播体操比赛中,计算每班的最后得分,是先去掉一个最高分和一个最低分,再算剩下的得分的平均分,把它作为该班的最后得分,你知道这是为什么吗?
因为裁判的疏忽、或者欣赏兴趣不同、或者个人情感等原因,造成有的分数过高或者过低。这些极端数据会影响平均数。去掉这些极端数据,就减弱了极端数据的影响。再求剩下的得分的平均分,又发挥了大多数评委的作用。这样做吸取了平均数和中位数的优点。
练一练
1、判断题:
(1)给定一组数据,那么描述这组数据的平均数一定只有一个。( )
(2)给定一组数据,那么描述这组数据的中位数一定只有一个。( )
(3)给定一组数据,那么描述这组数据的众数一定只有一个。 ( )
(4)给定一组数据,那么描述这组数据的平均数一定位于最大值和最小值之间。 ( )
(5)给定一组数据,那么描述这组数据的中位数一定位于最大值和最小值正中间。 ( )
(6)给定一组数据,如果找不到众数,那么众数一定就是0。 ( )
√
√
√
×
×
×
统计量
相同点
优点
缺点
求法
个数
平均数、中位数和众数的比较
中位数
众数
平均数
小结
都是数据的代表,从不同侧面反映了数据的集中程度
反映平均水平
反映中等水平
反映多数水平
易受极端
值的影响
不能全面
反映数据
有多个众数时没多大意义
公式
先排序后求数
出现次
数最多
唯一
唯一
不唯一
妈妈,我这次数学考试考了78分,而全班平均分只有77分,每次都最后几个,这次我在中上水平,进步很大啊!
你真棒!成绩单给妈妈看一下好吗?
我很生气!碰碰……
分数
100
91
90
86
78
15
6
人数
1
15
4
13
1
4
2
六(1)班第三单元数学成绩单
姓名:小新 成绩:78分 平均分:77分
为什么妈妈那么生气呢?我没有撒谎啊!
问:小新撒谎了吗?聪明的你能帮小新解开疑惑吗?小新哪句话讲的不合实际?
王刚
招聘会现场
我在找工作时,遇到了一件事,请同学们帮我解决一下。
招聘启示
本超市由于扩大规模,现招聘工作人员若干名,平均每人月工资2000元,有意者到我处面谈。
北山超市联系人:毛老板
2012年5月15日
你们超市忽悠了我,我的工资才1600元,不是招聘启示上说的2000元。
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
根据你的岗位,你每个月工资是1600元。
我们超市平均每人月工资确实是2000元,你看看公司的工资表。
毛老板
同学们,帮我算一下,毛老板说的对吗?
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
平均每人月工资
(5500+3000+2000+1700+1500+1100+1100+1100+1000)÷9
=18000÷9
=2000(元)
1、有多少人的工资超过了平均月工资?有多少人的工资低于了平均月工资?
2、是哪几个人的工资影响了平均月工资?
3、用平均数2000元能代表这一组数据准确吗?
平均数可以反映一组数据的整体水平,但是它容易受极端数据的影响。
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
员工C
小孙
我的月工资是1500元,
在超市属于中等水平。
1、怎么理解“在超市属于中等水平”?这1500在这组数据中处于什么位置?
2、这组数据是怎么排列的?换成由小到大排列,1500还在那个位置吗?
中位数
3、怎么理解“中位数”里面的“中”和“位”两个字?
将一组数据从小到大(或从大到小)排列,中间的数称为这组数据的中位数。
中:中间
位:位置
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
王刚
1600
刚才有9个数据,中位数在正中间。现在有十个数据,怎样求它们的中位数呢?请同学们自己试一试。
第一步,重新按顺序排列。
5500 3000 2000 1700 1600 1500 1100 1100 1100 1000
第二步,找正中间的两个数,求它们两个数的平均数。
(1600+1500)÷2
=3100 ÷2
=1550(元)
怎样求一组数据的中位数?
将一组数据由小到大或者由大到小排列。
(1)如果数据个数是奇数,则处于中间位置的数为这组数据的中位数。
(2)如果数据个数是偶数,则中间两个数据的平均数为这组数据的中位数。
比一比,看谁能快速找到我。
题号
数据
中位数
(1)
5 6 2 3 2
(2)
3 7 6 8 8 40 10
(3)
5 6 2 4 3 5
(4)
10 6 12 44 200 55 20 100
3
8
4.5
32
经理
副经理
员工A
员工B
员工C
员工D
员工E
员工F
员工G
月工资
5500
3000
2000
1700
1500
1100
1100
1100
1000
我们这里好几个人月工资都是1100元。
员工D
小骆
1、在这组数据中,1100有什么特点?
众数
一组数据中出现次数最多的数称为这组数据的众数。
2、怎么理解众数中“众”的意思?
众:多
下面各组数数据中有众数吗?如果有,找一找。
题号
数据
众数
(1)
40 50 65 33 50 70 50
(2)
3 2 6 7 6 5 3 3 6
(3)
3 0 1 5 9 14
(4)
2 3 5 5 3 2
50
3和6
没有
没有
观察这几组数,你知道了关于众数个数的哪些知识?
1、在一组数据中,可能不止一个众数。
2、在一组数据中,如果每个数据出现的次数相同,这组数据就没有众数。
平均数、中位数、众数是从不同的角度来描述一组数据。
下面不同情况,应该关注哪种数呢?
1、一次考试后,老师想了解全班整体水平怎么样,要关注全班分数的( )。
2、老师想了解全班哪个分数的人最多,要关注全班分数的( )。
3、一个学生想了解自己在全班处于中上还是中下水平,要关注全班分数的( )。
平均数
众数
中位数
比较三个统计量:
区别:三个统计量从不同的侧面提供了一组数据的面貌.
1、平均数:应用范围最广泛,比较可靠和稳定。它与这组数据中的每一个数据都有关系,能够最为充分地反映这组数据所包含的信息,在进行统计推断时有重要的作用。但容易受到极端数据的影响。
2、中位数:在一组数据的数值排序中处于中间位置,在统计 学分析中扮演“分水岭”的角色,人们通过中位数可以对事物大体趋势进行判断和掌控。
3、众数:着眼于各个数据出现次数多少的考察,其大小仅仅与一组数据的部分数据有关系。它反映一组数据的集中水平。
联系:三个统计量都可代表一组数据,表示数据的“平均水平,中等水平或多数水平”,都反映数据的集中趋势。
求出这组数的平均数、中位数和众数。
10 15 5 8 10 10 10 12
平均数是( )
中位数是( )
众数是( )
在一组数据中,有时平均数、中位数和众数可能相同。
10
10
10
在运动会进行跳绳比赛时,我班第一组九个女生1分钟时间跳的次数如下:
234 133 128 92 113 116 182 125 92
(1)分别计算这组数据的平均数和中位数。
(2)你认为平均数、中位数哪一个能更好地表示这组同学的跳绳水平?
中位数能更好地表示这组同学的跳绳水平。因为在一组数据中,有数据偏大或者偏小时,用中位数来代表这组数据的一般水平比平均数更合适。
平均数:(234+133+128+92+113+116+182+125+92 )÷9=135
中位数:234 182 133 128 125 116 113 92 92
中位数是125
在运动会中,五年级女子跳远预决赛成绩如下:
郑芳圆:3.6米 宋 敏 :3.2 米 刘炎炎:3.2米
杜 桦 :3.0米 张守宇:2.6米 崔咏琪:3.0米
根据这组数据,你能提哪些问题?
老师的问题:
(1)在这组数据中,平均数是多少?中位数是多少?众数是多少?
(2)崔咏琪在这6人中处于什么水平?
在运动会集体项目广播体操比赛中,计算每班的最后得分,是先去掉一个最高分和一个最低分,再算剩下的得分的平均分,把它作为该班的最后得分,你知道这是为什么吗?
因为裁判的疏忽、或者欣赏兴趣不同、或者个人情感等原因,造成有的分数过高或者过低。这些极端数据会影响平均数。去掉这些极端数据,就减弱了极端数据的影响。再求剩下的得分的平均分,又发挥了大多数评委的作用。这样做吸取了平均数和中位数的优点。
练一练
1、判断题:
(1)给定一组数据,那么描述这组数据的平均数一定只有一个。( )
(2)给定一组数据,那么描述这组数据的中位数一定只有一个。( )
(3)给定一组数据,那么描述这组数据的众数一定只有一个。 ( )
(4)给定一组数据,那么描述这组数据的平均数一定位于最大值和最小值之间。 ( )
(5)给定一组数据,那么描述这组数据的中位数一定位于最大值和最小值正中间。 ( )
(6)给定一组数据,如果找不到众数,那么众数一定就是0。 ( )
√
√
√
×
×
×
统计量
相同点
优点
缺点
求法
个数
平均数、中位数和众数的比较
中位数
众数
平均数
小结
都是数据的代表,从不同侧面反映了数据的集中程度
反映平均水平
反映中等水平
反映多数水平
易受极端
值的影响
不能全面
反映数据
有多个众数时没多大意义
公式
先排序后求数
出现次
数最多
唯一
唯一
不唯一
