华东师大版数学九年级上册 复习《三角形》(教案)
文档属性
| 名称 | 华东师大版数学九年级上册 复习《三角形》(教案) |
|
|
| 格式 | docx | ||
| 文件大小 | 60.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览


文档简介
教学设计——复习《三角形》
教学设计:
一:复习知识点
简单复习三角形全等、相似的几种证明方法,特殊三角形的性质和判定。
证明一般三角形全等的方法有 等(简写),
证明一般三角形相似的方法有 等(简写)。
证明直角三角形全等所特有的方法有 ,
证明直角三角形相似所特有的方法有 。
(可用符号语言)等腰三角形的性质有 ;
判定有 。
等边三角形的性质有 ;
判定有 。
具体操作:1、学生先独立完成;
2、6人小组互相补充;
3、教师多媒体对答案。
典例分析
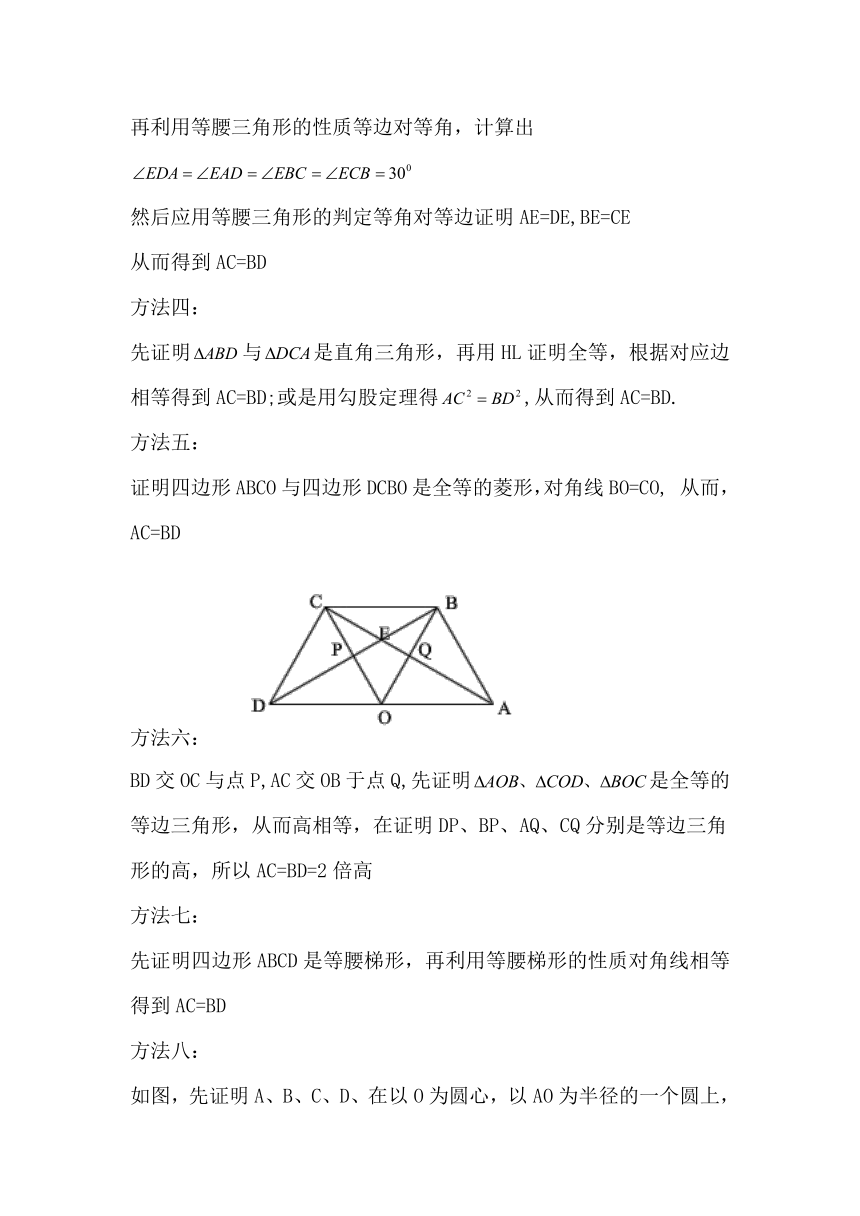
例:如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC,求证:BD=AC.你还能得出那些正确的结论呢?请选择其中的一个进行证明。
具体操作:
对于此问题要求学生课下独立思考并寻求解题方法;
学生单独完成至少一种解答,鼓励多种解答(给予充分的时间)
6人小组互相讨论交流补充不同的解题方法(学生讨论时教师巡视,指导,收集不同的解题方法)
教师将各小组不同的解题方法汇总,给予适当的点评和表扬;
根据不同的解答过程启发学生进一步思考,还能得出哪些正确的结论,教师将不同结论汇总,筛选并要求学生简要证明
学生解题方法摘录:
方法一:
证明,再用全等三角形对应边相等证明AC=BD
方法二:
证明,再用全等三角形对应边相等得到AC=BD
方法三:
先证明BO=DO CO=AO AB=BC=CD,
再利用等腰三角形的性质等边对等角,计算出
然后应用等腰三角形的判定等角对等边证明AE=DE,BE=CE
从而得到AC=BD
方法四:
先证明与是直角三角形,再用HL证明全等,根据对应边相等得到AC=BD;或是用勾股定理得,从而得到AC=BD.
方法五:
证明四边形ABCO与四边形DCBO是全等的菱形,对角线BO=CO, 从而,AC=BD
方法六:
BD交OC与点P,AC交OB于点Q,先证明是全等的等边三角形,从而高相等,在证明DP、BP、AQ、CQ分别是等边三角形的高,所以AC=BD=2倍高
方法七:
先证明四边形ABCD是等腰梯形,再利用等腰梯形的性质对角线相等得到AC=BD
方法八:
如图,先证明A、B、C、D、在以O为圆心,以AO为半径的一个圆上,再证明弧BD=弧AC,从而得到AC=BD,或者利用圆心角,从而得到AC=BD
学生得出的结论摘录:
四边形ABCD为等腰梯形,
四边形ABCD为菱形,
△CEB∽△AED且相似比为1:2,
△BQE∽△AQO
△CPE∽△DCE∽△DPC
OP=OQ
为等边三角形
OP为的中位线
课后变式训练
变式一:利用旋转进行变式
ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),则以上所得结论还成立吗?
变式二:利用平移进行变式
若点O是线段AD上一动点,则以上结论还成立吗?ΔOCD再绕点O旋转呢?
变式三:改变条件进行变式
若将ΔOAB和ΔOCD改为全等的等腰三角形呢?
教学反思:
学生开始独立完成解答时,一般都只能想到一两种解题方法,后来通过小组讨论交流之后,,学生思路被完全打开,也为证明其他没能想到的正确结论打下了基础。非常难得的是学生能广泛进行联想把所学的圆、四边形等知识与三角形密切联系起来,创造性地应用所学到的各种知识和方法解决问题,实现了知识的正向迁移,真正有效地提高了学生的问题解决能力。
设计意图:
本堂课是初三的一节复习课,立足于使学生牢固掌握基础知识和基本技能,并能灵活运用知识进行独立思考,选择具有典型性、探索性、多解性、拓展性的例题,并通过小组合作培养了学生思维的灵活性、深刻性、广阔性、批判性和创造性等良好的思维品质,从而有效地提高解题能力。
教学设计:
一:复习知识点
简单复习三角形全等、相似的几种证明方法,特殊三角形的性质和判定。
证明一般三角形全等的方法有 等(简写),
证明一般三角形相似的方法有 等(简写)。
证明直角三角形全等所特有的方法有 ,
证明直角三角形相似所特有的方法有 。
(可用符号语言)等腰三角形的性质有 ;
判定有 。
等边三角形的性质有 ;
判定有 。
具体操作:1、学生先独立完成;
2、6人小组互相补充;
3、教师多媒体对答案。
典例分析
例:如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC,求证:BD=AC.你还能得出那些正确的结论呢?请选择其中的一个进行证明。
具体操作:
对于此问题要求学生课下独立思考并寻求解题方法;
学生单独完成至少一种解答,鼓励多种解答(给予充分的时间)
6人小组互相讨论交流补充不同的解题方法(学生讨论时教师巡视,指导,收集不同的解题方法)
教师将各小组不同的解题方法汇总,给予适当的点评和表扬;
根据不同的解答过程启发学生进一步思考,还能得出哪些正确的结论,教师将不同结论汇总,筛选并要求学生简要证明
学生解题方法摘录:
方法一:
证明,再用全等三角形对应边相等证明AC=BD
方法二:
证明,再用全等三角形对应边相等得到AC=BD
方法三:
先证明BO=DO CO=AO AB=BC=CD,
再利用等腰三角形的性质等边对等角,计算出
然后应用等腰三角形的判定等角对等边证明AE=DE,BE=CE
从而得到AC=BD
方法四:
先证明与是直角三角形,再用HL证明全等,根据对应边相等得到AC=BD;或是用勾股定理得,从而得到AC=BD.
方法五:
证明四边形ABCO与四边形DCBO是全等的菱形,对角线BO=CO, 从而,AC=BD
方法六:
BD交OC与点P,AC交OB于点Q,先证明是全等的等边三角形,从而高相等,在证明DP、BP、AQ、CQ分别是等边三角形的高,所以AC=BD=2倍高
方法七:
先证明四边形ABCD是等腰梯形,再利用等腰梯形的性质对角线相等得到AC=BD
方法八:
如图,先证明A、B、C、D、在以O为圆心,以AO为半径的一个圆上,再证明弧BD=弧AC,从而得到AC=BD,或者利用圆心角,从而得到AC=BD
学生得出的结论摘录:
四边形ABCD为等腰梯形,
四边形ABCD为菱形,
△CEB∽△AED且相似比为1:2,
△BQE∽△AQO
△CPE∽△DCE∽△DPC
OP=OQ
为等边三角形
OP为的中位线
课后变式训练
变式一:利用旋转进行变式
ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),则以上所得结论还成立吗?
变式二:利用平移进行变式
若点O是线段AD上一动点,则以上结论还成立吗?ΔOCD再绕点O旋转呢?
变式三:改变条件进行变式
若将ΔOAB和ΔOCD改为全等的等腰三角形呢?
教学反思:
学生开始独立完成解答时,一般都只能想到一两种解题方法,后来通过小组讨论交流之后,,学生思路被完全打开,也为证明其他没能想到的正确结论打下了基础。非常难得的是学生能广泛进行联想把所学的圆、四边形等知识与三角形密切联系起来,创造性地应用所学到的各种知识和方法解决问题,实现了知识的正向迁移,真正有效地提高了学生的问题解决能力。
设计意图:
本堂课是初三的一节复习课,立足于使学生牢固掌握基础知识和基本技能,并能灵活运用知识进行独立思考,选择具有典型性、探索性、多解性、拓展性的例题,并通过小组合作培养了学生思维的灵活性、深刻性、广阔性、批判性和创造性等良好的思维品质,从而有效地提高解题能力。
