华东师大版数学九年级上册 23.3.3 相似三角形的性质 课件(共21张)
文档属性
| 名称 | 华东师大版数学九年级上册 23.3.3 相似三角形的性质 课件(共21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 199.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 14:16:01 | ||
图片预览






文档简介
(共21张PPT)
相似三角形的性质
相似三角形的性质:
①对应角相等
②对应边成比例(相似比)
相似三角形有哪些判定方法?
1.预备定理。
2.两角对应相等
3.两边对应成比例且夹角相等
4.三边对应成比例
单元导入,明确目标
相似三角形的对应高、对应中线及对应角平分线、周长、面积有何关系呢?
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平
分线、周长、面积的关系。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
自学指导、合作探究
自学内容:课本P
合作探究:
1.相似三角形对应高的比、对应角平分线的比、对应中线的比是多少?并说明理由。
2相似三角形的周长比、面积比为多少?并说明理由。
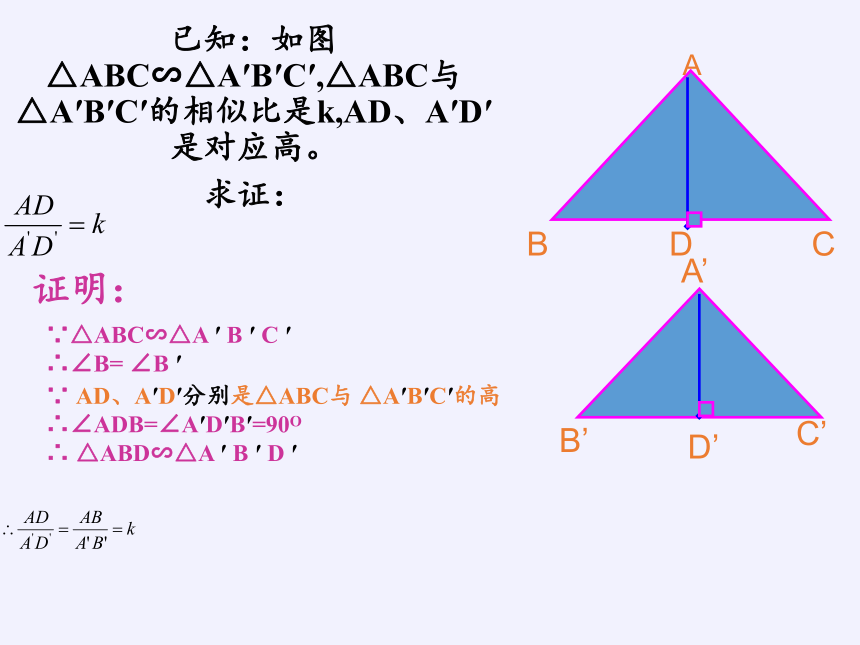
已知:如图△ABC∽△A′B′C′,△ABC与 △A′B′C′的相似比是k,AD、A′D′是对应高。
求证:
B’
A’
C’
D’
A
B
C
D
证明:
∵△ABC∽△A ′ B ′ C ′
∴∠B= ∠B ′
∵ AD、A′D′分别是△ABC与 △A′B′C′的高
∴∠ADB=∠A′D′B′=90O
∴ △ABD∽△A ′ B ′ D ′
我也做一做:
A、求证:相似三角形对应中线的比等于相似比。
B、求证:相似三角形对应角平分线的比等于相似比
大组汇报,教师点拨
A
C
B
B′
A′
C′
A
C
B
B′
A′
C′
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
A
B
C
A′
B′
C′
D
D′
证明:
∽ △
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
相似三角形的面积比为相似比的平方。
通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。是平方,平方!重要的事情说三遍!
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为2:5,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
2:5
2:5
4:25
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4 : 3
4 : 3
2:5
巩固达标
4.已知:梯形ABCD中,AD∥BC,AD=3cm,
BC=5cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=2cm,则OF=_______.
A
B
C
D
E
F
O
5. 如图,在 ABCD中,E是AB上一点,AC与DE相交于F,AE:EB=1:2,求 AEF与 CDF的相似比.若 AEF的面积为5平方厘米,求 CDF的面积。
D
B
F
E
C
A
D
自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是 ,周长比是 ,面积比是 .
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为 cm.
3、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4
(D)1:5
A
B
C
D
E
A
B
D
C
E
4. 在△ABC中,BC=2,DE∥BC,交AB于E,交AC于D, 则DE=_______。
小结
这节课你有什么收获呢
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
知识象一艘船
让它载着我们
驶向理想的
……
你今天努力了吗?
谢 谢
相似三角形的性质
相似三角形的性质:
①对应角相等
②对应边成比例(相似比)
相似三角形有哪些判定方法?
1.预备定理。
2.两角对应相等
3.两边对应成比例且夹角相等
4.三边对应成比例
单元导入,明确目标
相似三角形的对应高、对应中线及对应角平分线、周长、面积有何关系呢?
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平
分线、周长、面积的关系。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
自学指导、合作探究
自学内容:课本P
合作探究:
1.相似三角形对应高的比、对应角平分线的比、对应中线的比是多少?并说明理由。
2相似三角形的周长比、面积比为多少?并说明理由。
已知:如图△ABC∽△A′B′C′,△ABC与 △A′B′C′的相似比是k,AD、A′D′是对应高。
求证:
B’
A’
C’
D’
A
B
C
D
证明:
∵△ABC∽△A ′ B ′ C ′
∴∠B= ∠B ′
∵ AD、A′D′分别是△ABC与 △A′B′C′的高
∴∠ADB=∠A′D′B′=90O
∴ △ABD∽△A ′ B ′ D ′
我也做一做:
A、求证:相似三角形对应中线的比等于相似比。
B、求证:相似三角形对应角平分线的比等于相似比
大组汇报,教师点拨
A
C
B
B′
A′
C′
A
C
B
B′
A′
C′
相似三角形周长的比等于相似比。
已知:
求证:
∽△
△
证明:
∽△
△
∵
∴
∴
(相似三角形对应边成比例)
(等比性质)
A
C
B
B′
A′
C′
A
B
C
A′
B′
C′
D
D′
证明:
∽ △
△
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
相似三角形的面积比为相似比的平方。
通过前面的思考、探索、推理,我们得到相似三角形有如下性质;
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。是平方,平方!重要的事情说三遍!
1.如果两个三角形相似,相似比为3∶5,那么对应角的角平分线的比等于多少?
2.相似三角形对应边的比为2:5,那么相似比为______,对应角的角平分线的比为______,周长的比为______,面积的比为______.
3∶5
2:5
2:5
4:25
3、若两个三角形面积之比为16:9,则它们的对高之比为_____,对应中线之比为_____
4 : 3
4 : 3
2:5
巩固达标
4.已知:梯形ABCD中,AD∥BC,AD=3cm,
BC=5cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=2cm,则OF=_______.
A
B
C
D
E
F
O
5. 如图,在 ABCD中,E是AB上一点,AC与DE相交于F,AE:EB=1:2,求 AEF与 CDF的相似比.若 AEF的面积为5平方厘米,求 CDF的面积。
D
B
F
E
C
A
D
自我测试
1、两个矩形相似,它们的对角线之比是1:3,那么
它们的相似比是 ,周长比是 ,面积比是 .
2、若两个相似三角形的相似比是3:5,其中第一
个三角形的周长为21cm,则第二个三角形的
周长为 cm.
3、如图,已知△ABC∽△ADE,
且BC=2DE,则△ADE与四
边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4
(D)1:5
A
B
C
D
E
A
B
D
C
E
4. 在△ABC中,BC=2,DE∥BC,交AB于E,交AC于D, 则DE=_______。
小结
这节课你有什么收获呢
1、相似三角形对应高的比等于相似比,
相似三角形对应中线的比等于相似比,
相似三角形对应角平分线的比等于相似比。
2、相似三角形周长的比等于相似比,
相似三角形面积的比等于相似比的平方。
知识象一艘船
让它载着我们
驶向理想的
……
你今天努力了吗?
谢 谢
