2021-2022北师大版八上数学一次函数压轴题精选30题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022北师大版八上数学一次函数压轴题精选30题(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-05 22:11:18 | ||
图片预览


文档简介
北师大版八上数学一次函数压轴题精选30题
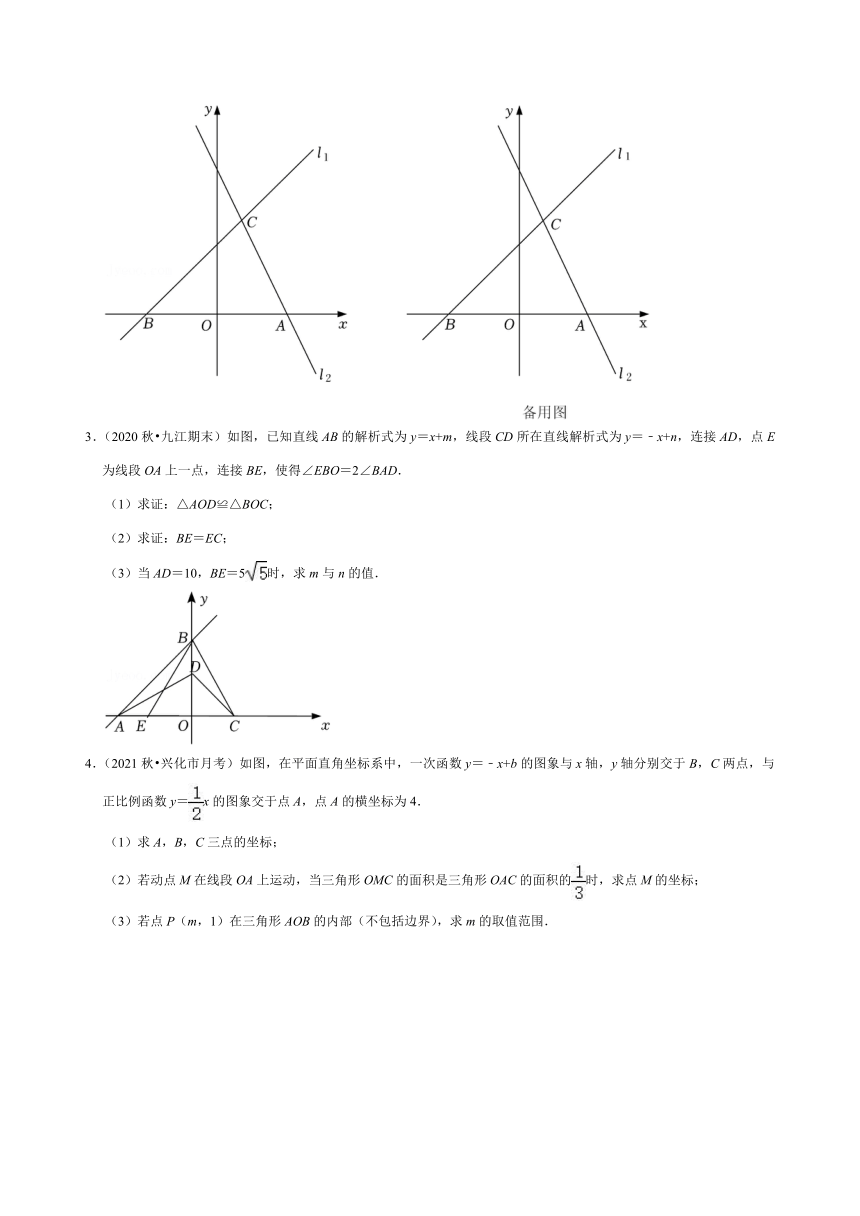
1.(2020秋 金台区校级期末)(1)问题解决:如图1,在平面直角坐标系xOy中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标.
(2)问题拓展:在图1中,点E是x轴上的一个动点,是否存在这样的点E,使得|EC﹣EB|的值最大?如果不存在,请说明理由,如果存在,求点E的坐标.
(3)类比探究:如图2,在平面直角坐标系xOy中,点A坐标(0,﹣6),点B坐标(8,0),过点B作x轴垂线l,点P是l上一动点,点D是在一次函数y=﹣2x+2图象上一动点,若△APD是以点D为直角顶点的等腰直角三角形,求出点D与点P的坐标.
2.(2020秋 济阳区期末)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
(3)在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
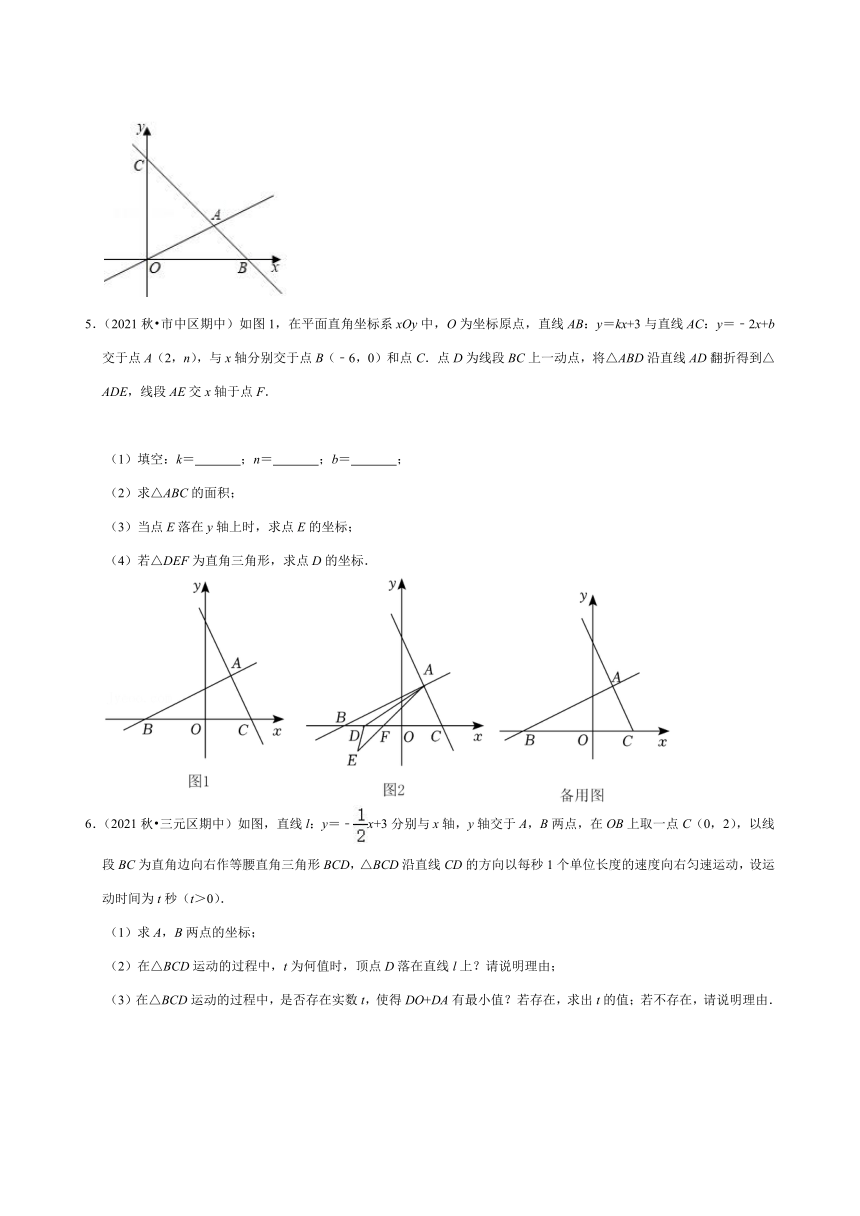
3.(2020秋 九江期末)如图,已知直线AB的解析式为y=x+m,线段CD所在直线解析式为y=﹣x+n,连接AD,点E为线段OA上一点,连接BE,使得∠EBO=2∠BAD.
(1)求证:△AOD≌△BOC;
(2)求证:BE=EC;
(3)当AD=10,BE=5时,求m与n的值.
4.(2021秋 兴化市月考)如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
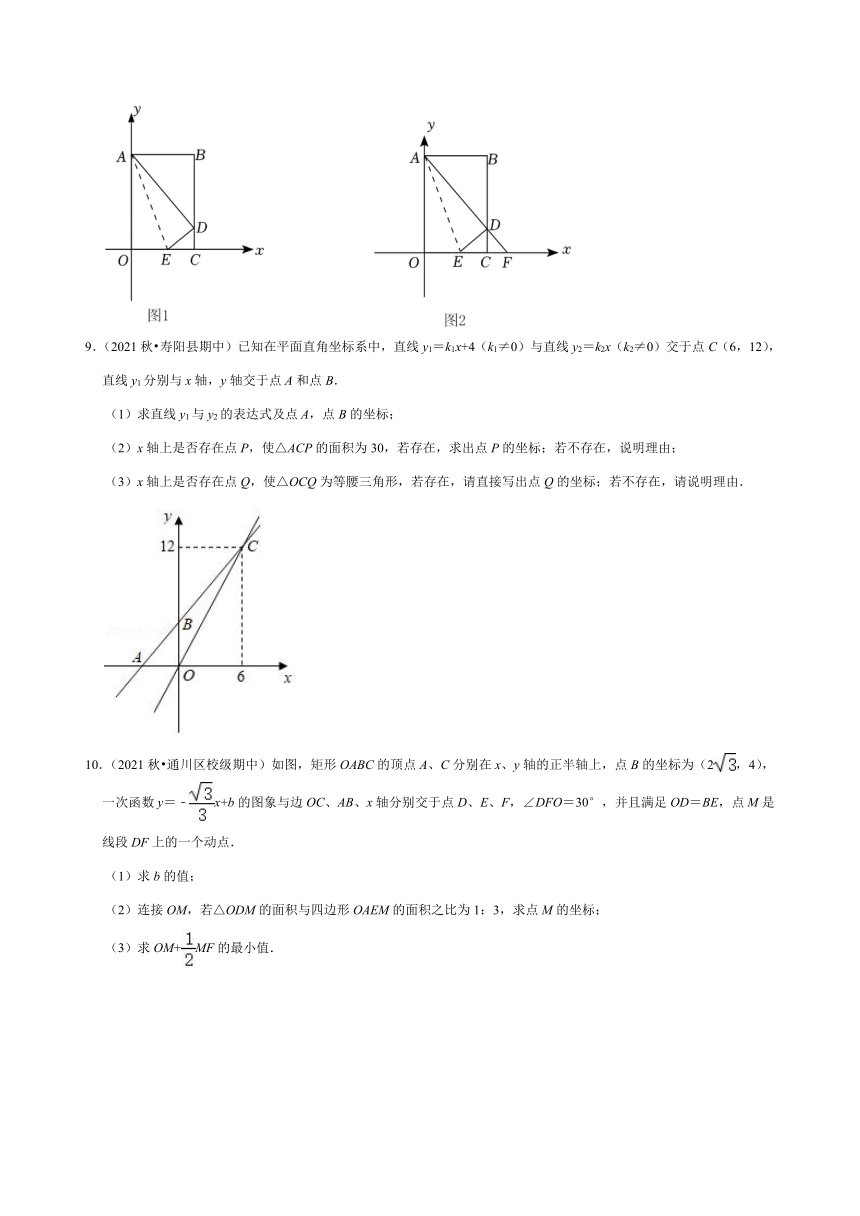
5.(2021秋 市中区期中)如图1,在平面直角坐标系xOy中,O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)填空:k= ;n= ;b= ;
(2)求△ABC的面积;
(3)当点E落在y轴上时,求点E的坐标;
(4)若△DEF为直角三角形,求点D的坐标.
6.(2021秋 三元区期中)如图,直线l:y=﹣x+3分别与x轴,y轴交于A,B两点,在OB上取一点C(0,2),以线段BC为直角边向右作等腰直角三角形BCD,△BCD沿直线CD的方向以每秒1个单位长度的速度向右匀速运动,设运动时间为t秒(t>0).
(1)求A,B两点的坐标;
(2)在△BCD运动的过程中,t为何值时,顶点D落在直线l上?请说明理由;
(3)在△BCD运动的过程中,是否存在实数t,使得DO+DA有最小值?若存在,求出t的值;若不存在,请说明理由.
7.(2021秋 雨城区校级期中)如图,直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)直接写出点A,B的坐标,并求出线段AB的长.
(2)猜想线段AF与BE之间的数量与位置关系,并证明;
(3)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=3,求CF的长.
8.(2021秋 介休市期中)在“综合与探究”课上,张老师让每名同学在练习本上画出一个长方形,随后以该长方形为基本图形,以小组为单位编制一道综合探究题.经过思考和讨论,励志小组向全班同学分享了他们编拟的试题,得到了侯老师的认可,同学们也眼前一亮,纷纷动手,开始了探究.请你也跟他们一起来完成这道试题吧.如图1,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐标系,已知AO=10,AB=6,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.
(1)分别求点D,E的坐标.
(2)如图2,若直线AD与x轴相交于点F,求直线AD表达式及点F的坐标.
(3)在(2)的条件下,P是x轴上的一动点,是否存在以A,P,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(4)在本题的探究过程中,你感悟到哪些数学思想,请至少写出两条.
9.(2021秋 寿阳县期中)已知在平面直角坐标系中,直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),直线y1分别与x轴,y轴交于点A和点B.
(1)求直线y1与y2的表达式及点A,点B的坐标;
(2)x轴上是否存在点P,使△ACP的面积为30,若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△OCQ为等腰三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
10.(2021秋 通川区校级期中)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(2,4),一次函数y=﹣x+b的图象与边OC、AB、x轴分别交于点D、E、F,∠DFO=30°,并且满足OD=BE,点M是线段DF上的一个动点.
(1)求b的值;
(2)连接OM,若△ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)求OM+MF的最小值.
11.(2021秋 深圳校级期中)如图所示,在平面直角坐标系中,直线y=x+1与y=﹣x+3分别交x轴于点B和点C,点D是直线y=﹣x+3与y轴的交点.
(1)求点B、C、D的坐标;
(2)设M(x,y)是直线y=x+1上一点,△BCM的面积为S,请写出S与x的函数关系式;来探究当点M运动到什么位置时,△BCM的面积为10,并说明理由.
(3)线段CD上是否存在点P,使△CBP为等腰三角形,如果存在,直接写出P点的坐标;如果不存在,请说明理由.
12.(2021秋 南岸区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4分别交x轴、y轴于点A、B,经过点B的直线y=﹣x+b交x轴于点C.
(1)求点C的坐标;
(2)动点P在射线AB上运动,过点P作PH⊥x轴,垂足为点H,交直线BC于点Q,设点P的横坐标为t.线段PQ的长为d(d≠0).求d关于t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,当点P在线段AB上时,连接CP,若S△CPQ=,在线段BC上取一点M.连接PM,使∠BPM+2∠ABO=90°,问在x轴上是否存在点R,使△PMR是以∠PMR为直角的直角三角形?若存在,请求出点R的坐标;若不存在,请说明理由.
13.(2021秋 本溪期中)已知一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、B,与直线y=x相交于点C,过B作x轴的平行线l,点P是直线l上的一个动点.
(1)直接写出点A、B的坐标:A 、B .
(2)若S△AOC=S△BCP,求点P的坐标;
(3)若点E是平面内的一个动点,当△ABE是AB为直角边的等腰直角三角形,则点E的坐标为 .
14.(2021秋 金牛区校级期中)如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
15.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
16.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
17.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
18.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
19.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 ,F的坐标为 ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 .
20.(2021秋 和平区期中)已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.
(1)点A的坐标 ,点B的坐标 ;
(2)若S△AOC=S△BCP,求点P的坐标.
(3)若点E是直线y=x上的一个动点,当△APE是以AE为斜边的等腰直角三角形时,点E的坐标为 .
(4)在(3)的条件下,当点P在AE右侧时,Q为平面内一点,EQ=2,连接OQ,将线段OQ绕着点O逆时针旋转90°,得到线段OM,连接QM,EM,直接写出EM的范围.
21.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,请直接写出点M的坐标 ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 .
22.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
23.(2021秋 龙华区校级期中)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D.过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD的长;
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;
(3)当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 .
24.(2021秋 南海区期中)如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
25.(2021秋 龙岗区校级期中)如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求直线CD的函数解析式;
(3)在直线AB上,是否存在点P,使得S△POD=S△OCD,若存在,请直接写出点P的坐标;若不存在,说明理由.
26.(2021 古冶区一模)如图,直角坐标系xOy中,过点A(6,0)的直线l1与直线l2:y=kx﹣1相交于点C(4,2),直线l2与x轴交于点B.
(1)k的值为 ;
(2)求l1的函数表达式和S△ABC的值;
(3)直线y=a与直线l1和直线l2分别交于点M,N,(M,N不同)
①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以MN为边作正方形MNDE,边DE恰好在x轴上,直接写出此时a的值.
27.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点D在l2上.
(1)①直接写出点C的坐标为 ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
28.(2021春 任城区校级期末)如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
29.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
30.(2021春 渝中区校级期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
(1)若直线AB解析式为y=﹣2x+12,求:
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值及此时点P的坐标;若不存在,说明理由.
参考答案与试题解析
1.(2020秋 金台区校级期末)(1)问题解决:如图1,在平面直角坐标系xOy中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标.
(2)问题拓展:在图1中,点E是x轴上的一个动点,是否存在这样的点E,使得|EC﹣EB|的值最大?如果不存在,请说明理由,如果存在,求点E的坐标.
(3)类比探究:如图2,在平面直角坐标系xOy中,点A坐标(0,﹣6),点B坐标(8,0),过点B作x轴垂线l,点P是l上一动点,点D是在一次函数y=﹣2x+2图象上一动点,若△APD是以点D为直角顶点的等腰直角三角形,求出点D与点P的坐标.
【解答】解:(1)对于一次函数y=x+1,
令x=0,y=1,
∴B(0,1),
令y=0,则x+1=0,
∴x=﹣4,
∴A(﹣4,0),
∴OA=4,OB=1,
过点C作CD⊥x轴于D,
∴∠ADC=∠BOA=90°,
∴∠CAD+∠ACD=90°,
∵∠BAC=90°,
∴∠CAD+∠BAO=90°,
∴∠CAD=∠ABO,
∵△ABC是等腰直角三角形,
∴AC=AB,
在△ADC和△BOA中,
,
∴△ADC≌△BOA(AAS),
∴CD=OA=4,AD=OB=1,
∴OD=OA+AD=5,
∴C(﹣5,4);
(2)存在点E,使得|EC﹣EB|的值最大.
延长CB交x轴于E,
∵BC=|CE﹣EB|,BC>=|CE′﹣E′B|,
∴点E即为所求,
设直线CB的解析式为y=kx+b,
∵B(0,1),C(﹣5,4),
∴,
解得:,
∴直线CB的解析式为y=﹣x+1,
当y=0时,﹣x+1=0,解得:x=,
∴E(,0);
(3)如图,过点D作DF⊥y轴于F,延长FD交BP于G,
∵点A坐标(0,﹣6),点B坐标(8,0),
∴DF+DG=OB=8,
∵点D在直线y=﹣2x+2上,
∴设点D(m,﹣2m+2),
∴F(0,﹣2m+2),OF=|2m﹣2|,AF=|2m﹣2﹣6|=|2m﹣8|,
∵BP⊥x轴,B(8,0),
∴G(8,﹣2m+2),
同(1)的方法得,△AFD≌△DGP(AAS),
∴AF=DG,DF=PG,
∵DF+DG=DF+AF=8,
∴m+|2m﹣8|=8,
∴m=或m=0,
∴D(0,2)或(,﹣),
当m=0时,G(8,2),DF=0,
∴PG=0,
∴P(8,2),
当m=时,﹣2m+2=﹣2×+2=﹣,
∴G(8,﹣),DF=m=,
∴BG=,
∴P(8,),
即:D(0,2),P(8,2)或D(,﹣),P(8,).
2.(2020秋 济阳区期末)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
(3)在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)把(1,m)代入y=x+3得m=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,把C(1,4),A(3,0)代入得:
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)如图:
在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
∴AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=|3a﹣3|,
∵MN=AB,
∴|3a﹣3|=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2);
(3)存在,设P(t,0),则CP2=(t﹣1)2+16,BP2=(t+3)2,
而BC2=(1+3)2+(4﹣0)2=32,
①当BP=CP时,如图:
∴(t+3)2=(t﹣1)2+16,
解得t=1,
∴P(1,0);
②当BC=BP时,如图:
∴(t+3)2=32,
解得t=﹣3+4或t=﹣3﹣4,
∴P(﹣3+4,0)或(﹣3﹣4,0),
③当BC=CP时,如图:
∴(t﹣1)2+16=32,
解得t=5或t=﹣3(与B重合,舍去),
∴P(5,0),
综上所述,P的坐标为:(1,0)或(﹣3+4,0)或(﹣3﹣4,0)或(5,0).
3.(2020秋 九江期末)如图,已知直线AB的解析式为y=x+m,线段CD所在直线解析式为y=﹣x+n,连接AD,点E为线段OA上一点,连接BE,使得∠EBO=2∠BAD.
(1)求证:△AOD≌△BOC;
(2)求证:BE=EC;
(3)当AD=10,BE=5时,求m与n的值.
【解答】(1)证明:在y=x+m中,令x=0,则y=m,令y=0,则x=﹣m,
∴A(﹣m,0),B(0,m),
∴OA=OB=m,
在y=﹣x+n中,令x=0,则y=n,令y=0,则x=n,
∴C(n,0),D(0,n),
∴OC=OD=n,
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS);
(2)证明:由(1)知,OA=OB,OC=OD,∠AOB=∠COD=90°,
∴∠OAB=∠OBA=∠ODC=∠CDO=45°,
∵△AOD≌△BOC,
∴∠ADB=∠BCO,
∵∠ADO=∠ABO+∠BAD=45°+∠BAD,
∠BCO=∠DCO+∠BCD,
∴∠BAD=∠BCD,
设∠BAD=∠DCB=α,则∠EBO=2∠BAD=2α,
∴∠DBC=45°﹣α,
∵∠ECB=∠DCO+∠BCD=45°+α,
∠EBC=∠EBO+∠CBO=2α+45°﹣α=45°+α,
∴∠ECB=∠EBC,
∴BE=EC;
(3)解:由(1)知OA=OB=m,OC=OD=n,
∵∠AOD=∠BOE=90°,
∴AO2+OD2=AD2,OB2+OE2=BE2,
∵AD=10,BE=CE=5,
∴m2+n2=102,m2+(5﹣n)2=(5)2,
∴m=4,n=2.
4.(2021秋 兴化市月考)如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
【解答】解:(1)∵点A在正比例函数y=x的图象上,且点A的横坐标为4.
∴点A(4,2),
∵一次函数y=﹣x+b的图象与正比例函数y=x的图象交于点A,
∴2=﹣4+b,
∴b=6,
∴一次函数解析式为y=﹣x+6,
∵一次函数y=﹣x+6的图象与x轴,y轴分别交于B,C两点,
∴点B(6,0),点C(0,6);
(2)由(1)可知:OC=6,xA=4,
∴S△OAC=×OC×xA=×6×4=12,
∵S△OMC=S△OAC=4,
∴S△OMC=×OC×|xM|=4,
∴|xM|=,
∴xM=±,
当动点M在线段OA上时,x>0,则当x=时,y=×=,
∴此时M点的坐标为(,);
(3)∵点P(m,1)在△AOB的内部(不包括边界),
∴当y=1时,代入正比例函数中得:1=x,
解得:x=2,
当y=1时,代入一次函数中得:1=﹣x+6,
解得:x=5,
∴2<m<5.
故答案为:2<m<5.
5.(2021秋 市中区期中)如图1,在平面直角坐标系xOy中,O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)填空:k= ;n= 4 ;b= 8 ;
(2)求△ABC的面积;
(3)当点E落在y轴上时,求点E的坐标;
(4)若△DEF为直角三角形,求点D的坐标.
【解答】解:(1)把B(﹣6,0)代入kx+3,
∴﹣6k+3=0,
∴k=,
∴直线AB解析式:y=x+3,
把点A(2,n)代入y=x+3,
∴n=4,
∴A(2,4),
把(2,4)代入y=﹣2x+b得,
﹣4+b=4,
∴b=8,
故答案为:;4;8;
(2)∵直线AC:y=﹣2x+8,
∴点C(4,0),
∵点A(2,4),点B(﹣6,0)和点C(4,0),
∴BC=10,△ABC的BC边上的高为4,
∴S△ABC=×10×4=20;
(3)如图,过点A作AH⊥y轴于点H,
∴AH=2,AE2=AB2=(﹣6﹣2)2+42=80,
∴HE==2,
∴OE=HE﹣OH=2﹣4,
∴E点的坐标为(0,4﹣2);
(4)△DEF为直角三角形,分两种情况讨论:
当∠EDF=90°时,
如图,由对折可得,∠ADB=∠ADE==135°,
∴∠ADO=135°﹣90°=45°,
过点A作AG⊥BC于G,
∴AG=DG=4,
∵OG=2,
∴OD=2,
∴D(﹣2,0);
当∠DFE=90°时,
由对折得,AE=AB==4,BD=DE,
∴EF=4﹣4,
由A、B两点坐标可得:BF=2﹣(﹣6)=8,
设DF=m,则BD=8﹣m,
∴DE=8﹣m,
∴(8﹣m)2=m2+(4﹣4)2,
∴m=2﹣2,
∴OD=DF﹣OF=2﹣2﹣2=2﹣4,
∴D(4﹣2,0),
综上,D(﹣2,0)或(4﹣2,0).
6.(2021秋 三元区期中)如图,直线l:y=﹣x+3分别与x轴,y轴交于A,B两点,在OB上取一点C(0,2),以线段BC为直角边向右作等腰直角三角形BCD,△BCD沿直线CD的方向以每秒1个单位长度的速度向右匀速运动,设运动时间为t秒(t>0).
(1)求A,B两点的坐标;
(2)在△BCD运动的过程中,t为何值时,顶点D落在直线l上?请说明理由;
(3)在△BCD运动的过程中,是否存在实数t,使得DO+DA有最小值?若存在,求出t的值;若不存在,请说明理由.
【解答】解:(1)∵y=﹣x+3分别与x轴,y轴交于A,B两点,
∴当x=0时,y=3,当y=0时,x=6,
∴点A(6,0),点B(0,3);
(2)∵点C(0,2),点B(0,3),
∴BC=1,
∵△BCD是等腰直角三角形,
∴CD=BC=1,∠BCD=90°,
∴点D(1,2),
若顶点D落在直线l上,
∴当y=2时,则2=﹣x+3,
∴x=2,
∴t==1;
(3)如图,作点O关于直线CD的对称点O',连接O'A交直线CD于点D',此时,D'O+D'A有最小值;
∵点O与点O'关于直线CD对称,
∴O'(0,4),
设直线O'A的解析式为y=kx+4,
∴0=6k+4,
∴k=﹣,
∴直线O'A的解析式为y=﹣x+4,
当y=2时,2=﹣x+4,
∴x=3,
∴t==2,
当t=2时,使得DO+DA有最小值.
7.(2021秋 雨城区校级期中)如图,直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)直接写出点A,B的坐标,并求出线段AB的长.
(2)猜想线段AF与BE之间的数量与位置关系,并证明;
(3)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=3,求CF的长.
【解答】解:(1)直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,
令x=0,则y=﹣4,
∴B(0,﹣4),
∴OB=4,
令y=0,则x﹣4=0,
∴x=4,
∴A(4,0),
∴OA=4,
∴AB==4;
(2)猜想:AF=BE,AF⊥BE,
证明:∵OE⊥OF,OA⊥OB,
∴∠FOA=∠EOB,
∵点A(4,0),点B(0,﹣4),
∴OA=OB,
在△FOA和△EOB中,
,
∴△FOA≌△EOB(SAS),
∴AF=BE,∠FAO=∠EBO,
∵∠EBO+∠OAB=90°,
∴∠FAO+∠OAB=90°,即∠FAB=90°,
∴AF⊥BE,
∴AF=BE,AF⊥BE;
(3)连接CE,
∵OA=OB=4,AB=4,BE=3,
∴AF=BE=3,AE=,
∵OE=OF,OM⊥EF,
∴OM是线段EF的垂直平分线,
∴CF=CE,
设CF=x,则CE=x,AC=3﹣x,
在Rt△ACE中,CE2=AE2+AC2,即x2=()2+(3﹣x)2,
解得,x=,即CF=.
8.(2021秋 介休市期中)在“综合与探究”课上,张老师让每名同学在练习本上画出一个长方形,随后以该长方形为基本图形,以小组为单位编制一道综合探究题.经过思考和讨论,励志小组向全班同学分享了他们编拟的试题,得到了侯老师的认可,同学们也眼前一亮,纷纷动手,开始了探究.请你也跟他们一起来完成这道试题吧.如图1,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐标系,已知AO=10,AB=6,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.
(1)分别求点D,E的坐标.
(2)如图2,若直线AD与x轴相交于点F,求直线AD表达式及点F的坐标.
(3)在(2)的条件下,P是x轴上的一动点,是否存在以A,P,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(4)在本题的探究过程中,你感悟到哪些数学思想,请至少写出两条.
【解答】解:(1)如图1,由折叠得:AD=AO=10,OE=DE,
Rt△ABD中,AB=6,
∴BD===8,
∵OA=BC=10,
∴CD=10﹣8=2,
∴D(6,2),
设OE=x,则EC=6﹣x,
由勾股定理得:DE2=EC2+CD2,
∴x2=(6﹣x)2+22,
解得:x=,
∴E(,0);
(2)设AD的解析式为:y=kx+b,
把A(0,10)和D(6,2)代入得:
,
解得:,
∴AD的解析式为:y=﹣x+10,
当y=0时,﹣x+10=0,
∴x=,
∴F(,0);
(3)①当AP=AF时,
∵AO⊥x轴,F(,0),
∴OP=OF=,
∴P(﹣,0);
②当AF=FP时,
由勾股定理得:AF==,
∴OP′=﹣=5,OP=+=20,
∴P′(﹣5,0),P(20,0);
③当AP=FP时,
由勾股定理得:FP2=AP2=OP2+OA2,
∴(OP+)2=OP2+102,
解得:OP=,
∴P(﹣,0),
综上,点P的坐标为(﹣,0)或(﹣5,0)或(20,0)或(﹣,0);
(4)在本题的探究过程中,由(1)可知利用数形结合的思想,由(2)和(1)列方程可解答,利用了方程思想,由(3)运用了分类讨论的思想.
9.(2021秋 寿阳县期中)已知在平面直角坐标系中,直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),直线y1分别与x轴,y轴交于点A和点B.
(1)求直线y1与y2的表达式及点A,点B的坐标;
(2)x轴上是否存在点P,使△ACP的面积为30,若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△OCQ为等腰三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),
∴12=6k1+4,12=6k2,
解得:k1=,k2=2,
∴y1=x+4,y2=2x,
在y1=x+4中,当y1=0时,x=﹣3,
∴A(﹣3,0),
当x=0时,当y1=4,
∴B(0,4);
(2)存在,理由如下:
设P(m,0),
∵A(﹣3,0),C(6,12),
∴AP=|m+3|,
∵△ACP的面积为30,
∴×12×|m+3|=30
解得:m=2或﹣8,
∴P(2,0)或P(﹣8,0);
(3)∵点C(6,12),
∴OC===6,
当OC=OQ时,如图:
OC=OQ=6,
∵点Q的坐标为(﹣6,0)或(6,0);
当CO=CQ时,如图:作CD⊥x轴于D,
∵CO=CQ,
∴DQ=OD=6,
∴OQ=12,
∴点Q的坐标为(12,0);
当CQ=OQ时,如图:
∵CQ=OQ,CQ2=122+(OQ﹣6)2,
∴OQ2=122+(OQ﹣6)2,解得OQ=15,
∴点Q的坐标为(15,0).
综上所述,存在点Q,使△OCQ为等腰三角形,点Q的坐标为(﹣6,0)或(6,0)或(12,0)或(15,0).
10.(2021秋 通川区校级期中)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(2,4),一次函数y=﹣x+b的图象与边OC、AB、x轴分别交于点D、E、F,∠DFO=30°,并且满足OD=BE,点M是线段DF上的一个动点.
(1)求b的值;
(2)连接OM,若△ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)求OM+MF的最小值.
【解答】解:(1)y=﹣x+b中,令x=0,解得y=b,则点D的坐标是(0,b),OD=b,
∵OD=BE,
∴BE=b,
∵点B的坐标为(2,4),
∴点E的坐标为(2,4﹣b),
把E点坐标代入y=﹣x+b得4﹣b=﹣2+b,
解得b=3;
(2)∵b=3,点D的坐标是(0,b),点E的坐标为(2,4﹣b),
∴点D的坐标是(0,3),点E的坐标为(2,1),
∴OD=3,AE=1,OA=2,
∵S四边形OAED=(OD+AE) OA=×(3+1)×2=4,
∵△ODM的面积与四边形OAEM的面积之比为1:3,
∴△ODM的面积与四边形OAED的面积之比为1:4,
∴S△ODM=S四边形OAED=,
设点M的横坐标是a,则 3a=,解得a=,
把x=a=代入y=﹣x+3得y=﹣×+3=,
∴点M的坐标是(,);
(3)过点M作MN⊥x轴交于点N,
∵∠DFO=30°,
∴MN=MF,
∴OM+MF=OM+MN,
作点O关于一次函数的对称点O',过点O'作x轴的垂线交x轴于点N',交一次函数于点M′,
∴OM′=O′M′,
∴OM+MN的最小值=OM′+M′N′,
当O′、M′、N′在同一直线时,OM′+M′N′的值最小,为O'N',
∵∠DFO=30°,
∴∠ODF=60°,∠DOM=30°,∠O'ON'=90°﹣30°=60°,
在Rt△ODM中,OM=OD =3×=,
∴OO′=2OM=3,
在Rt△ON'O'中,
N'=OO′ =3×=.
∴OM+MF的最小值为.
11.(2021秋 深圳校级期中)如图所示,在平面直角坐标系中,直线y=x+1与y=﹣x+3分别交x轴于点B和点C,点D是直线y=﹣x+3与y轴的交点.
(1)求点B、C、D的坐标;
(2)设M(x,y)是直线y=x+1上一点,△BCM的面积为S,请写出S与x的函数关系式;来探究当点M运动到什么位置时,△BCM的面积为10,并说明理由.
(3)线段CD上是否存在点P,使△CBP为等腰三角形,如果存在,直接写出P点的坐标;如果不存在,请说明理由.
【解答】(1)解:把y=0代入y=x+1得:0=x+1,
∴x=﹣1,
∴B(﹣1,0),
当x=0时,y=﹣x+3=0,
∴D(0,3),
把y=0代入y=﹣x+3得:0=﹣x+3,
∴x=4,
∴C(4,0),
即B(﹣1,0),C(4,0),D(0,3);
(2)解:BC=4﹣(﹣1)=5,∵M(x,y)在y=x+1上,
∴M(x,x+1),
过M作MN⊥x轴于N,
①当M在x轴的上方时,MN=x+1,
∴S=BC MN=×5×(x+1)=x+;
②当M在x轴的下方时,MN=|x+1|=﹣x﹣1,
∴S=BC MN=×5×(﹣x﹣1)=﹣x﹣;
把S=10代入得:10=x+得:x=3,x+1=4;
把S=10代入y=﹣x﹣得:x=5=﹣5,x+1=﹣4;
∴M(3,4)或(﹣5,﹣4)时,s=10;
即S与x的函数关系式是,点M运动到(3,4)或(﹣5,﹣4)时,△BCM的面积为10;
(3)解:∵C(4,0),D(0,3),
∴OC=4,OD=3,
在Rt△OCD中,
由勾股定理得:CD===5,
有三种情况:
①CB=CP=5时,此时P与D重合,P的坐标是(0,3);
②BP=PC时,此时P在BC的垂直平分线上,P的横坐标是x==,
代入y=﹣x+3得:y=,
∴P的坐标是(,);
③BC=BP时,设P(x,﹣x+3),
根据勾股定理得:(x+1)2+(﹣x+3﹣0)2=52,
解得:x=﹣或x=4,
∵P在线段CD上,
∴x=﹣(舍去),
当x=4时,与C重合,(舍去);
∴存在点P,使△CBP为等腰三角形,P点的坐标是(0,3)或(,).
12.(2021秋 南岸区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4分别交x轴、y轴于点A、B,经过点B的直线y=﹣x+b交x轴于点C.
(1)求点C的坐标;
(2)动点P在射线AB上运动,过点P作PH⊥x轴,垂足为点H,交直线BC于点Q,设点P的横坐标为t.线段PQ的长为d(d≠0).求d关于t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,当点P在线段AB上时,连接CP,若S△CPQ=,在线段BC上取一点M.连接PM,使∠BPM+2∠ABO=90°,问在x轴上是否存在点R,使△PMR是以∠PMR为直角的直角三角形?若存在,请求出点R的坐标;若不存在,请说明理由.
【解答】解:(1)直线y=2x+4,当x=0时,y=4;
当y=0时,则2x+4=0,
解得x=﹣2,
∴A(﹣2,0),B(0,4),
∵直线y=﹣x+b经过点B(0,4),
∴b=4,
∴直线y=﹣x+b的解析式为y=﹣x+4,
当y=0时,则﹣x+4=0,
解得x=4,
∴C(4,0).
(2)∵PH⊥x轴于点H,交直线BC于点Q,且点P的横坐标为t,
∴P(t,2t+4),Q(t,﹣t+4),
如图1,点P在y轴的左侧,则﹣2≤t<0,
∵PQ=﹣t+4﹣(2t+4)=﹣3t,
∴d=﹣3t(﹣2≤t<0);
如图2,点P在y轴的右侧,则t>0,
∵PQ=2t+4﹣(﹣t+4)=3t,
∴d=3t(t>0),
综上所述,d关于t的函数解析式为.
(3)存在,
如图3,连接OP,PM交y轴于点F,∠PMR=90°,作PE⊥y轴于点E,
∵点P在线段AB上,且S△CPQ=,
∴×(﹣3t)(4﹣t)=,
整理得t=﹣1或t=5(不符合题意,舍去),
∴P(﹣1,2),E(0,2),
∴点P为AB的中点,
∵∠AOB=90°,
∴OP=AB=PB,
∴∠ABO=∠POB,
∴∠APO=∠ABO+∠POB=2∠ABO,
∵∠BPM+2∠ABO=90°,
∴∠BPM+∠APO=90°,
∴∠OPF=90°,
∵∠OEP=90°,OE=2,PE=1,
∴OP==,
∵S△POF=OF PE=PF OP,
∴PF=OF=OF=OF,
∵PF2+OP2=OF2,
∴(OF)2+()2=OF2,
解得OF=,
∴F(0,),
设直线PF的解析式为y=kx+,则﹣k+=2,
解得k=,
∴直线PF的解析式为y=x+,
由得,
∴M(1,3),
设直线OP的解析式为y=mx,则﹣m=2,
解得m=﹣2,
∴直线OP的解析式为y=﹣2x,
∵∠PMR+∠OPF=180°,
∴MR∥OP,
设直线MR的解析式为y=﹣2x+n,则﹣2+n=3,
解得n=5,
∴直线MR的解析式为y=﹣2x+5,
当y=0时,则﹣2x+5=0,
解得x=,
∴点R的坐标为(,0).
13.(2021秋 本溪期中)已知一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、B,与直线y=x相交于点C,过B作x轴的平行线l,点P是直线l上的一个动点.
(1)直接写出点A、B的坐标:A (8,0) 、B (0,6) .
(2)若S△AOC=S△BCP,求点P的坐标;
(3)若点E是平面内的一个动点,当△ABE是AB为直角边的等腰直角三角形,则点E的坐标为 (6,14)或(﹣6,﹣2)或(14,8)或(2,﹣8) .
【解答】解:(1)对于y=﹣x+6,
当x=0时,y=6;
当y=0时,则﹣x+6=0,解得x=8,
∴A(8,0),B(0,6).
(2)如图1,过点C作CD⊥x轴于点D,交直线l于点E,
由得,
∴C(3,),
∴D(3,0),E(3,6),
∴CD=,CE=6=,
设P(x,6),
∵S△AOC=S△BCP,且BP=|x|
∴×8×=×|x|,
解得x=或x=,
∴P(,6)或P′(,6),
∴点P的坐标为(,6)或(,6).
(3)如图2,EB=BA,且∠ABE=90°,点E在y轴右侧,
作EG⊥y轴于点G,则∠BGE=∠AOB=90°,
∴∠EBG=90°﹣∠ABO=∠BAO,
∴△BGE≌△AOB(ASA),
∴GB=OA=8,GE=OB=6,
∴OG=OB+GB=6+8=14,
∴E(6,14);
如图2,E′B=BA,且∠ABE′=90°,点E′在y轴左侧,
∵E′B=EB,
∴点E′与点E关于点B成中心对称,
∴E′(﹣6,﹣2);
如图3,AE=BA,且∠BAE=90°,点E在x轴上方,
作EH⊥x轴于点H,则∠EHA=∠AOB=90°,
∴∠EAH=90°﹣∠OAB=∠ABO,
∴△EHA≌△AOB(ASA),
∴HE=OA=8,HA=OB=6,
∴OH=OA+HA=8+6=14,
∴E(14,8);
如图3,AE′=BA,且∠BAE′=90°,点E′在x轴下方,
∵E′A=EA,
∴点E′与点E关于点A成中心对称,
∴E′(2,﹣8),
综上所述,点E的坐标为(6,14)或(﹣6,﹣2)或(14,8)或(2,﹣8).
14.(2021秋 金牛区校级期中)如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
【解答】解:(1)∵直线y=x+1与x轴、y轴分别交于点C、E,
∴C(﹣2,0),E(0,1),
设直线BC的解析式为y=kx+b,
根据题意得,
解得,
∴直线BC的解析式为y=2x+4;
∵A(4,0),B(0,4),
设直线AB的解析式为y=ax+4,
∴4a+4=0,解得a=﹣1,
∴直线AB的解析式为y=﹣x+4,
∵直线y=x+1与线AB交于点D.
联立得,解得,
∴D(2,2);
(2)过点D作DH⊥x轴于H,
∵D(2,2),E(0,1),A(4,0),
∴DH=2,OH=2,OE=1,OA=4,AH=4﹣2=2,
∴S四边形OADE=S梯形OHDE+S△ADH=×2×(1+2)+×2×2=5;
(3)∵F是OA的中点,A(4,0),
∴F(2,0),
∴AF=OF=2,
设直线l与四边形OADE的另一交点为M,M的纵坐标为y,直线l恰好将四边形OADE分成面积比为1:4的两部分,即直线MF恰好将四边形OADE分成面积比为1:4的两部分,
分两种情况:
①当点M在点F右侧时,S△AMF:S五边形OFMDE=1:4,如图:
∵S四边形OADE=5,
∴S△AMF=1,
∴AF y=1,即×2y=1,解得y=1,
∵点M在直线AB:y=﹣x+4上,
∴1=﹣x+4,解得x=3,
∴点M(3,1),
由F,M两点坐标可求得直线FM的解析式为y=x﹣2,即直线l的解析式为y=x﹣2;
②当点M在点F右左侧时,S△OMF:S五边形MFADE=1:4,如图:
∵S四边形OADE=5,
∴S△OMF=1,
∴AF y=1,即×2y=1,解得y=1,
∴点M与点E重合,
∴点M(0,1),
由F,M两点坐标可求得直线FM的解析式为y=﹣x+1,即直线l的解析式为y=﹣x+1;
综上可知,直线l的解析式为y=x﹣2或y=﹣x+1.
15.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
【解答】(1)解:∵+(a﹣4)2=0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4,
则OA=OB=4.
∵AH⊥BC即∠AHC=90°,∠COB=90°,
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA);
(2)证明:过O分别作OM⊥CB于M点,作ON⊥HA于N点.
在四边形OMHN中,∠MON=360°﹣3×90°=90°,
∴∠COM=∠PON=90°﹣∠MOP.
∵△OAP≌△OBC,
∴OC=OP,
在△COM与△PON中,
,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=∠CHA=45°;
(3)证明:如图:连接OD.
∵∠AOB=90°,OA=OB,D为AB的中点,
∴OD⊥AB,∠BOD=∠AOD=45°,OD=DA=BD,
∴∠OAD=45°,∠MOD=90°+45°=135°,
∴∠DAN=135°=∠MOD.
∵MD⊥ND即∠MDN=90°,
∴∠MDO=∠NDA=90°﹣∠MDA.
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN.
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
16.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
【解答】解:(1)对于直线l2的解析式为y=﹣x+3,令x=0,得到y=3,
∴B(0,3),
令y=0,得到x=6,
∴A(6,0).
∴点A是坐标为(6,0),点B的坐标为(0,3);
(2)联立y=x,y=﹣x+3并解得:x=2,
∴点C(2,2),
∴S△COB=OB xC=×3×2=3;
(3)存在.
∵点B(0,3),点C(2,2),
∴BC==,
设P(0,y),
①当PC=BC=时,如图,
又∵点C(2,2),
∴PC2=22+(2﹣y)2,
∴()2=22+(2﹣y)2,
∴y=1或3,
∵y=3时,与点B重合,故舍去,
∴点P(0,1);
②当BP=BC=时,如图,
OP=OB+PB=3+,OP′=OB﹣P′B=3﹣,
∴点P(0,3+),(0,3﹣);
③当PB=PC时,如图,
∵PB2=PC2,
∴(3﹣y)2=22+(2﹣y)2,
∴解得:y=,
∴点P(0,),
综上所述:点P坐标为(0,3+),(0,3﹣),(0,1),(0,).
17.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
【解答】解:(1)当x=0时,y=﹣2k;当y=0时,x=2,
∴点B坐标为(0,﹣2k),点A坐标(2,0),
∴OA=2,OB=﹣2k,
∵OA=OB,
∴k=﹣1,
∴直线l的函数表达式为y=﹣x+2;
(2)在Rt△OAD中,AD=,OA=2,
∴OD==1,
∵∠OEB=∠ADO=∠AOB=90°,
∴∠BOE+∠OBE=90°,∠BOE+∠AOD=90°,
∴∠OBE=∠AOD,
∵OB=OA,
在Rt△OBE和Rt△AOD中,
,
∴△OBE≌△AOD(AAS),
∴BE=OD=1;
(3)点P始终在直线y=x上运动,
理由:如图3,过P作PE⊥x轴于E,PF⊥y轴于F,
则∠PFO=∠PEO=∠AOB=90°,
∴∠EPF=90°,
∵△ABP是等腰直角三角形,
∴∠APB=90°,PA=PB,
∴∠BPF=∠APE,
在△PBF与△PAE中,
,
∴△PBF≌△PAE(AAS),
∴PF=PE,
∴点P到x轴的距离等于点P到y轴的距离,
∴动点P在直线y=x(x>1)上运动.
18.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 A或B 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=|x+3|,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=|x+3﹣(﹣x+3)|=|x|,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=3,
∵PQ=BC,
∴|x|=3,解得:x=2或﹣2,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
19.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 (,6﹣) ,F的坐标为 (,2) ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 3或1 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 (0,8)或(0,2)或p(0,﹣2)或(0,) .
【解答】解:(1)∵正比例函数y=kx的图象过点C(2,4),
∴2k=4,
解得k=2,
∴正比例函数的表达式为y=2x;
∵一次函数y=﹣x+b的图象与正比例函数y=kx的图象交于点C(2,4),
∴4=﹣2+b,
∴b=6,
∴一次函数的表达式为:y=﹣x+6;
(2)∵点G在一次函数y=﹣x+6上,点F在正比例函数y=2x上,且点F.G.E在直线l上,E (m,0),m=,
∴点F、点G横坐标都为,
分别代入一次函数y=﹣x+6,正比例函数y=2x,
∴点G的纵坐标为y=﹣+6=6﹣,点F的纵坐标为y=2,
∴点G的坐标为(,6﹣),F的坐标为(,2),
∴FG=2﹣(6﹣)=3﹣6,
∴S△CFG=×(3﹣6)×(﹣2)=.
故答案为:(,6﹣),(,2),;
(3)①当点F在G点上方,即m>2时,
由(2)知点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=2m﹣(﹣m+6)=3m﹣6,
当GF=3时,3m﹣6=3,
解得:m=3;
②当F点在G点下方,即m<2时,
点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=(﹣m+6)﹣2m=﹣3m+6,
当GF=3时,﹣3m+6=3,
解得:m=1,
综上,m的值为3或1,
故答案为:3或1;
(4)①当CP=CO时,过点C作CM⊥y轴于M,△PCO为等腰三形,
∴PM=OM,
∵C(2,4),
∴OM=4.
∴PM=4,
∴P(0,8);
②当OP=OC时,
:C(2,4),
∴OC==2,
∴OP=2,
∴P(0,2)或p(0,﹣2);
③当PO=PC时,设P(0,y),
∴PO=|y|,PC==,
解得:y=,
∴P(0,).
故答案为:(0,8)或(0,2)或p(0,﹣2)或(0,).
20.(2021秋 和平区期中)已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.
(1)点A的坐标 (8,0) ,点B的坐标 (0,6) ;
(2)若S△AOC=S△BCP,求点P的坐标.
(3)若点E是直线y=x上的一个动点,当△APE是以AE为斜边的等腰直角三角形时,点E的坐标为 (,)或(16,20) .
(4)在(3)的条件下,当点P在AE右侧时,Q为平面内一点,EQ=2,连接OQ,将线段OQ绕着点O逆时针旋转90°,得到线段OM,连接QM,EM,直接写出EM的范围.
【解答】解:(1)在y=﹣x+6中,令y=0,
得﹣x+6=0,
解得:x=8,
∴A(8,0),
令x=0,得y=6,
∴B(0,6),
故答案为:(8,0),(0,6);
(2)由题意得:,
解得:,
∴C(3,),
∵直线l∥x轴,经过B(0,6),点P是直线l上的一个动点
∴P(x,6),
∴BP=|x|,
如图①,过点C作CG⊥OA于G,延长GC交BP于H,
则∠AGC=∠HGO=90°=∠BOG,
∵BP∥OA,
∴∠BHG=∠AGC=90°,
∴∠BHG=∠HGO=∠BOG=90°,
∴四边形BOGH是矩形,
∴GH=OB=6,
∵CG=,
∴CH=GH﹣CG=6﹣=,
∵S△AOC=S△BCP,
∴OA CG=BP CH,
即×8×= |x| ,
∴|x|=,
∴x=±,
∴P(,6)或(﹣,6);
(3)设点E(m,m)、点P(n,6),
∵△APE是以AE为斜边的等腰直角三角形,
∴PE=PA,∠APE=90°,
如图②,过点P作PF⊥OA于F,过点E作EK⊥PF于K,
则∠PKE=∠AFP=90°,
∴∠EPK+∠APF=90°,∠APF+∠PAF=90°,
∴∠EPK=∠PAF,
∴△PEK≌△APF(AAS),
∴EK=PF=6,PK=AF,
∵EK=|m﹣n|,PK=KF﹣PF=m﹣6,AF=|8﹣n|,
∴|m﹣n|=6,m﹣6=|8﹣n|,
解得:或,③
∴E(,)或(16,20);
(4)如图③,由(3)得E(,)或(16,20),
∵点P在AE右侧,
∴E(16,20),
∵EQ=2,
∴点Q在以E为圆心,半径为2的⊙E上运动,将OE绕点O逆时针旋转90°,得到ON,
以N为圆心,半径为2,作⊙N,连接EN交⊙N于M1,延长EN交⊙N于M2,
∵ON=OE==4,∠EON=90°,
∴EN=OE=4,
∵NM1=NM2=2,
∴EM的最小值为EM1=EN﹣NM1=4﹣2,
EM的最大值为EM2=EN+NM2=4+2,
∴EM的范围为4﹣2≤EM≤4+2.
21.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 y=﹣x+3 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 (﹣,) ;
②若△PQB的面积为,请直接写出点M的坐标 (,0)或(﹣,0) ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 (,0) .
【解答】解:(1)对于y=x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣x+3,
故答案为:y=﹣x+3;
(2)①设点M(m,0),
∴P(m,m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣,
∴P(﹣,),
故答案为:(﹣,);
②设点M(n,0),
∵点P在直线AB:y=x+3上,
∴P(n,n+3),
∵点Q在直线BC:y=﹣x+3上,
∴Q(n,﹣n+3),
∴PQ=|n+3﹣(﹣n+3)|=|n|,
∵△PQB的面积为,
∴S△PQB=|n| |n|=n2=,
∴n=±,
∴M(,0)或(﹣,0),
故答案为:(,0)或(﹣,0);
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,
∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,
∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,
∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,
∴EF=OK=,K(0,),
设F(x,0),则OE=x+,EH=OF=x,则H(x+,x),
∵C(6,0),K(0,),
设直线CK的解析式为y=kx+b,
∴,解得:,
∴直线CK的解析式为y=﹣x+,
∵点H在CK上,H(x+,x),
∴x=﹣(x+)+,解得:x=,
∴点F的坐标为(,0).
故答案为:(,0).
22.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 (1,7) .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组,得,
所以点C的坐标为(1,7),
故答案为:(1,7);
(2)∵M是直线AB上一点,
设点M的坐标为(a,a+6),
∵MN∥x轴,点N是直线y=﹣2x+9上一点,
∴a+6=﹣2x+9,解得x=,
∴点N的坐标是(,a+6),
∵MN=6,
∴|﹣a|=6,解得:a=5或﹣3,
∴点M的坐标为(5,11)或(﹣3,3);
(3)存在,
①点M的坐标为(﹣3,3)时,点N的坐标为(3,3),
∴MN=6,MC==,NC==,
设点P的坐标为(x,y),
∵直线y=x+6交x轴于点A,交y轴于点B,
∴B(0,6),OB=6=MN,
当BP=NC,OP=MC时;
,解得:或,
∴点P的坐标为(4,4)或(﹣4,4),
当BP=MC,OP=NC时,
,解得:或,
∴点P的坐标为(4,2)或(﹣4,2),
②点M的坐标为(5,11)时,点N的坐标为(﹣1,11),
∴MN=6,MC==,NC==,
此时△MNC与①中的△MNC三边都对应相等,所以此时情况与①相同.
综上,点P的坐标为(4,4)或(﹣4,4)或(4,2)或(﹣4,2).
23.(2021秋 龙华区校级期中)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D.过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD的长;
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;
(3)当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 4 .
【解答】解:(1)由题意知△BEO≌△AOD,
∴OE=AD,
∵k=﹣1,
∴y=﹣x+4,
∴B(0,4),
∴OB=4,
∵BE=3,
∴OE=,
∴;
(2)当k=﹣时,y=﹣,
∴当x=3时,y=0,
∴A(3,0),
①当BM⊥AB,且BM=AB时,
过点M作MN⊥y轴,
∴△BMN≌△ABO(AAS),
∴MN=OB,BN=OA,
∴MN=4,BN=3,
∴M(4,7);
②当AB⊥AM,且AM=AB时,
过点M作x轴垂线MK,
∴△ABO≌△AMK(AAS),
∴OB=AK,OA=MK,
∴AK=4,MK=3,
∴M(7,3);
③当AM⊥BM,且AM=BM时,
过点M作MH⊥x轴,MG⊥y轴,
∴△BMG≌△AHM(AAS),
∴BG=AH,GM=MH,
∴4﹣MH=MH﹣3,
∴MH=,
∴M();
综上所述:M(7,3)或(4,7)或();
(3)如图,将线段OB绕点B逆时针旋转90°得BE,连接EQ,
∴∠ABO=∠EBQ,
又∵AB=BQ,OB=BE,
∴△ABO≌△QBE(SAS),
∴∠BEQ=∠BOA=90°,
∴点Q在直线x=4上运动,
∴OQ的最小值为4,
故答案为:4.
24.(2021秋 南海区期中)如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
【解答】解:(1)把A(4,0)代入得:m=3,
一次函数解析式为,
令x=0,得y=3,
∴B(0,3),
在Rt△AOB中,AB2=OA2+OB2,
∴AB=5,
∵BC=AB=5,
∴C(0,﹣2),
∴;
(2)①设,
∴P在线段AB上,
∴0<t<4,
设直线AC的解析式为y=kx+b,代入A(4,0),C(0,﹣2)得,
∴,
∴,
又∵PQ∥y轴,则,
∴,
∴S四边形APOQ=S△AOP+S△AOQ=AO×|yP|+AO×|yQ|=×4×PQ=×4×(5﹣t)=,
又∵,
∴,解得t=1;
②如图所示,当N点在x轴下方时,
∵BP=AM,
∴BP+AP=AM+AP=AB,
∴PM=AB=5,
∵△PMN是以PM为直角边的等腰直角三角形,
当∠NPM=90°时,PN=PM=5,,
设,
过P点作直线M'N'∥x轴,作MM'⊥M'N',NN'⊥M'N',
∴MM'∥OB,
∴∠ABO=∠PMM',
在△AOB与△PM'M中,
,
∴△AOB≌△PM'M(AAS),
∴MM'=OB=3,PM'=OA=4,
∵∠NPN'+∠MPM'=90°,∠NPN'+∠N'NP=90°,
∴∠MPM'=∠N'NP,
在△PNN'与△MPM'中,
,
∴△PNN'≌△MPM'(AAS),
∴PN'=MM'=3,NN'=PM'=4,
∴M'N'=7,作MH⊥NN',则NH=1,
∵,
∴,
∴M在直线AB上,
∴,
,
,
a=﹣1,
∴,
∴.
当N点在x轴上方时,点N'与关于A(4,0)对称,
则,即,
综上:存在一点或使△PMN是以PM为直角边的等腰直角三角形.
25.(2021秋 龙岗区校级期中)如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 (8,0) ,点B的坐标为 (0,4) ;
(2)求直线CD的函数解析式;
(3)在直线AB上,是否存在点P,使得S△POD=S△OCD,若存在,请直接写出点P的坐标;若不存在,说明理由.
【解答】解:(1)令x=0,则y=4,
∴B(0,4),
令y=0,则0=﹣x+4,
∴x=8,
∴A(8,0),
故答案为:(8,0),(0,4);
(2)设OC=a,则AC=8﹣a,
由折叠知,BC=AC=8﹣a,
在Rt△BOC中,OB=4,
根据勾股定理得,BC2﹣OC2=OB2,
∴(8﹣a)2﹣a2=16,
∴a=3,
即:OC=3,
∴C(3,0),
∵△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
A(8,0),B(0,4),
∴D(4,2),
设CD的函数解析式为:y=kx+b,
则,
解得,
∴直线CD的函数解析式为:y=2x﹣6;
(3)点P在OD下方时,过点C作OD的平行线交AB于P,
∵D(4,2),
∴直线OD的解析式为:y=x,
∴设直线CP的函数解析式为:y=x+b,将C(3,0)代入得:b=﹣,
∴直线CP的函数解析式为:y=,
∴=﹣x+4,
解得x=,
∴y=,
∴点P(),
当点P在OD上方时,则点D为PP'的中点,
∴P'(,),
综上:点P()或(,).
26.(2021 古冶区一模)如图,直角坐标系xOy中,过点A(6,0)的直线l1与直线l2:y=kx﹣1相交于点C(4,2),直线l2与x轴交于点B.
(1)k的值为 ;
(2)求l1的函数表达式和S△ABC的值;
(3)直线y=a与直线l1和直线l2分别交于点M,N,(M,N不同)
①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以MN为边作正方形MNDE,边DE恰好在x轴上,直接写出此时a的值.
【解答】解:(1)将点C(4,2)代入y=kx﹣1得,
2=4k﹣1,
解得,
故答案为:;
(2)设直线l1的表达式为y=k1x+b
将点A(6,0),C(4,2)代入得,
,
解得,
∴直线l1的表达式为y=﹣x+6,
当y=0时,,
解得x=,
∴点B的坐标为(,0),
∴AB=6﹣=,
∴S△ABC=;
(3)①当x=0时,y=x﹣1=﹣1,
y=﹣x+6=6,
∴M,N都在y轴右侧时a的取值范围是:﹣1<a<6且a≠2.
②当y=a时,x﹣1=a,则x=,
∴点N的坐标为(,a),
当y=a时,﹣x+6=a,则x=6﹣a,
∴点M的坐标为(6﹣a,a)
∴MN=|6﹣a﹣|=||,
∵四边形MNDE为正方形,
∴||=|a|,
解得:或,
∴或.
27.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点D在l2上.
(1)①直接写出点C的坐标为 (2,1) ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
【解答】解(1)①∵y=kx﹣2k+1经过定点C,
∴点C的坐标与k的取值无关,
∴x=2时,y=1,
∴C(2,1),
故答案为:(2,1);
②设l2的解析式为:y=ax,
把C(2,1)代入y=ax得:a=,
∴l2的解析式为y=,
(2)如图,取OB的中点H,连接CH,
∵C(2,1),
∵S△BOC=2S△BCD,
当点D在线段OC上时,
则点D为OC的中点,
∴D(1,);
当点D在线段DC的延长线时,
∴S△BCD=,
即OB=,|xD|=3,
∴D(3,),
综上所述,符合条件的点D坐标为(1,)或(3,).
(3)过点C作CH∥EF,过点O作OH⊥OC,分别过点C,H作CM⊥OB于M,MN⊥OB于N,
∵∠EDO=45°,
∴∠OCH=45°,
∴OC=OH,
又∵∠MOC=∠NHO,∠OMC=∠ONH,
∴△COM≌△OHN(AAS),
∴CM=OH,OM=NH,
由C(2,1)得:H(1,﹣2),
∴yCH=3x﹣5,
由E(0,﹣)得:yEF=3x﹣,
∴P(,0),
过点F作FK⊥OA于K,
∵PF=PE,
∴△OPE≌△FPK(AAS),
∴F(1,),
将F(1,)代入l1:y=kx﹣2k+1,
∴k﹣2k+1=,
解得k=﹣.
28.(2021春 任城区校级期末)如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
【解答】解:(1)∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,
∴∠BCO=∠CDE,
在△BOC与△CED中,
,
∴Rt△BOC≌Rt△CED(AAS);
(2)设直线AB解析式为y=kx+b,把A(6,0),B(0,2)代入上式得:,
解得,
故直线AB的解析式为,
∵△BOC≌△CED,
∴CO=DE,
设CO=DE=m,而OB=CE=2,
∴D(m+2,m),
∵点D在直线上,把D(m+2,m)代入上式并解得m=1,
∴D(3,1),
(3)存在,理由如下:
设点P的坐标为(t,0),
而点C,D的坐标分别为(1,0),(3,1),
由点P,C,D的坐标得:PC2=(t﹣1)2,PD2=(t﹣3)2+1,CD2=22+1=5,
当PC=PD时,则(t﹣1)2=(t﹣3)2+1,
解得:t=,
当PC=CD时,则(t﹣1)2=5,
解得:t=,
当PD=CD时,则(t﹣3)2+1=5,
解得:t=5或t=1(舍去),
故P的坐标为或或或(5,0).
29.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
【解答】解:(1)∵直线y=﹣x+b(b>0)平分矩形OABC的面积,
∴直线过矩形的中心,
∵B(12,6),
∴矩形中心为(6,3),
∴﹣6+b=3,
解得b=12;
(2)如图,假设存在ON平分∠CNM的情况,
当PM与线段BC,OA交于N,M时,
过点O作OH⊥MN于H,
∵ON平分∠CNM,OC⊥BC,OH⊥MN,
∴OH=OC=6,
∵OP=12,
∴∠OPN=30°,
∴OM=OP =4,
当y=0时,﹣,解得x=8,
∴OD=8,
∴DM=OD﹣OM=8﹣4;
当PM与直线BC,OA交于N,M时,如图,
同理可得,此时DM=OD+OM=8+4,
综上:存在ON平分∠CNM的情况,此时DM=8﹣4或8+4;
(3)设平移后的直线y=﹣与y轴交于点P',沿此直线折叠,点O的对应点恰好落在BC边上F处,连接P'F,OF,
则有OP'=P'F=m,CP'=m﹣6,
在Rt△CP'F中,由勾股定理得:
(m﹣6)2+92=m2,
解得m=,
∴PP'=12﹣=,
∴a=.
30.(2021春 渝中区校级期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
(1)若直线AB解析式为y=﹣2x+12,求:
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值及此时点P的坐标;若不存在,说明理由.
【解答】解:(1)如图1,
①联立方程组得,
解得,
∴点C的坐标为(4,4);
②在y=﹣2x+12中,当x=0时y=12,
当y=0时,﹣2x+12=0,解得x=6,
∴点B(0,12),A(6,0),
则△OAC的面积为×6×4=12;
(2)由题意,在OC上截取OM=OP,连接MQ,
∵ON平分∠AOC,
∴∠AOQ=∠COQ,
又OQ=OQ.
∴△POQ≌△MOQ(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小,
即AQ+PQ存在最小值;
∵AB⊥ON,
∴∠AEO=∠CEO,
..△AEO≌△CEO(ASA),
∴OC=OA=4,
在Rt△OAM中,∵∠AOM=45°,
∴OM=AM=OA=2.
此时OP=OM=2,故P(2,0)
1.(2020秋 金台区校级期末)(1)问题解决:如图1,在平面直角坐标系xOy中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标.
(2)问题拓展:在图1中,点E是x轴上的一个动点,是否存在这样的点E,使得|EC﹣EB|的值最大?如果不存在,请说明理由,如果存在,求点E的坐标.
(3)类比探究:如图2,在平面直角坐标系xOy中,点A坐标(0,﹣6),点B坐标(8,0),过点B作x轴垂线l,点P是l上一动点,点D是在一次函数y=﹣2x+2图象上一动点,若△APD是以点D为直角顶点的等腰直角三角形,求出点D与点P的坐标.
2.(2020秋 济阳区期末)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
(3)在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
3.(2020秋 九江期末)如图,已知直线AB的解析式为y=x+m,线段CD所在直线解析式为y=﹣x+n,连接AD,点E为线段OA上一点,连接BE,使得∠EBO=2∠BAD.
(1)求证:△AOD≌△BOC;
(2)求证:BE=EC;
(3)当AD=10,BE=5时,求m与n的值.
4.(2021秋 兴化市月考)如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
5.(2021秋 市中区期中)如图1,在平面直角坐标系xOy中,O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)填空:k= ;n= ;b= ;
(2)求△ABC的面积;
(3)当点E落在y轴上时,求点E的坐标;
(4)若△DEF为直角三角形,求点D的坐标.
6.(2021秋 三元区期中)如图,直线l:y=﹣x+3分别与x轴,y轴交于A,B两点,在OB上取一点C(0,2),以线段BC为直角边向右作等腰直角三角形BCD,△BCD沿直线CD的方向以每秒1个单位长度的速度向右匀速运动,设运动时间为t秒(t>0).
(1)求A,B两点的坐标;
(2)在△BCD运动的过程中,t为何值时,顶点D落在直线l上?请说明理由;
(3)在△BCD运动的过程中,是否存在实数t,使得DO+DA有最小值?若存在,求出t的值;若不存在,请说明理由.
7.(2021秋 雨城区校级期中)如图,直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)直接写出点A,B的坐标,并求出线段AB的长.
(2)猜想线段AF与BE之间的数量与位置关系,并证明;
(3)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=3,求CF的长.
8.(2021秋 介休市期中)在“综合与探究”课上,张老师让每名同学在练习本上画出一个长方形,随后以该长方形为基本图形,以小组为单位编制一道综合探究题.经过思考和讨论,励志小组向全班同学分享了他们编拟的试题,得到了侯老师的认可,同学们也眼前一亮,纷纷动手,开始了探究.请你也跟他们一起来完成这道试题吧.如图1,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐标系,已知AO=10,AB=6,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.
(1)分别求点D,E的坐标.
(2)如图2,若直线AD与x轴相交于点F,求直线AD表达式及点F的坐标.
(3)在(2)的条件下,P是x轴上的一动点,是否存在以A,P,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(4)在本题的探究过程中,你感悟到哪些数学思想,请至少写出两条.
9.(2021秋 寿阳县期中)已知在平面直角坐标系中,直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),直线y1分别与x轴,y轴交于点A和点B.
(1)求直线y1与y2的表达式及点A,点B的坐标;
(2)x轴上是否存在点P,使△ACP的面积为30,若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△OCQ为等腰三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
10.(2021秋 通川区校级期中)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(2,4),一次函数y=﹣x+b的图象与边OC、AB、x轴分别交于点D、E、F,∠DFO=30°,并且满足OD=BE,点M是线段DF上的一个动点.
(1)求b的值;
(2)连接OM,若△ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)求OM+MF的最小值.
11.(2021秋 深圳校级期中)如图所示,在平面直角坐标系中,直线y=x+1与y=﹣x+3分别交x轴于点B和点C,点D是直线y=﹣x+3与y轴的交点.
(1)求点B、C、D的坐标;
(2)设M(x,y)是直线y=x+1上一点,△BCM的面积为S,请写出S与x的函数关系式;来探究当点M运动到什么位置时,△BCM的面积为10,并说明理由.
(3)线段CD上是否存在点P,使△CBP为等腰三角形,如果存在,直接写出P点的坐标;如果不存在,请说明理由.
12.(2021秋 南岸区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4分别交x轴、y轴于点A、B,经过点B的直线y=﹣x+b交x轴于点C.
(1)求点C的坐标;
(2)动点P在射线AB上运动,过点P作PH⊥x轴,垂足为点H,交直线BC于点Q,设点P的横坐标为t.线段PQ的长为d(d≠0).求d关于t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,当点P在线段AB上时,连接CP,若S△CPQ=,在线段BC上取一点M.连接PM,使∠BPM+2∠ABO=90°,问在x轴上是否存在点R,使△PMR是以∠PMR为直角的直角三角形?若存在,请求出点R的坐标;若不存在,请说明理由.
13.(2021秋 本溪期中)已知一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、B,与直线y=x相交于点C,过B作x轴的平行线l,点P是直线l上的一个动点.
(1)直接写出点A、B的坐标:A 、B .
(2)若S△AOC=S△BCP,求点P的坐标;
(3)若点E是平面内的一个动点,当△ABE是AB为直角边的等腰直角三角形,则点E的坐标为 .
14.(2021秋 金牛区校级期中)如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
15.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
16.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
17.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
18.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
19.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 ,F的坐标为 ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 .
20.(2021秋 和平区期中)已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.
(1)点A的坐标 ,点B的坐标 ;
(2)若S△AOC=S△BCP,求点P的坐标.
(3)若点E是直线y=x上的一个动点,当△APE是以AE为斜边的等腰直角三角形时,点E的坐标为 .
(4)在(3)的条件下,当点P在AE右侧时,Q为平面内一点,EQ=2,连接OQ,将线段OQ绕着点O逆时针旋转90°,得到线段OM,连接QM,EM,直接写出EM的范围.
21.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,请直接写出点M的坐标 ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 .
22.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
23.(2021秋 龙华区校级期中)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D.过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD的长;
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;
(3)当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 .
24.(2021秋 南海区期中)如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
25.(2021秋 龙岗区校级期中)如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求直线CD的函数解析式;
(3)在直线AB上,是否存在点P,使得S△POD=S△OCD,若存在,请直接写出点P的坐标;若不存在,说明理由.
26.(2021 古冶区一模)如图,直角坐标系xOy中,过点A(6,0)的直线l1与直线l2:y=kx﹣1相交于点C(4,2),直线l2与x轴交于点B.
(1)k的值为 ;
(2)求l1的函数表达式和S△ABC的值;
(3)直线y=a与直线l1和直线l2分别交于点M,N,(M,N不同)
①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以MN为边作正方形MNDE,边DE恰好在x轴上,直接写出此时a的值.
27.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点D在l2上.
(1)①直接写出点C的坐标为 ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
28.(2021春 任城区校级期末)如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
29.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
30.(2021春 渝中区校级期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
(1)若直线AB解析式为y=﹣2x+12,求:
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值及此时点P的坐标;若不存在,说明理由.
参考答案与试题解析
1.(2020秋 金台区校级期末)(1)问题解决:如图1,在平面直角坐标系xOy中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标.
(2)问题拓展:在图1中,点E是x轴上的一个动点,是否存在这样的点E,使得|EC﹣EB|的值最大?如果不存在,请说明理由,如果存在,求点E的坐标.
(3)类比探究:如图2,在平面直角坐标系xOy中,点A坐标(0,﹣6),点B坐标(8,0),过点B作x轴垂线l,点P是l上一动点,点D是在一次函数y=﹣2x+2图象上一动点,若△APD是以点D为直角顶点的等腰直角三角形,求出点D与点P的坐标.
【解答】解:(1)对于一次函数y=x+1,
令x=0,y=1,
∴B(0,1),
令y=0,则x+1=0,
∴x=﹣4,
∴A(﹣4,0),
∴OA=4,OB=1,
过点C作CD⊥x轴于D,
∴∠ADC=∠BOA=90°,
∴∠CAD+∠ACD=90°,
∵∠BAC=90°,
∴∠CAD+∠BAO=90°,
∴∠CAD=∠ABO,
∵△ABC是等腰直角三角形,
∴AC=AB,
在△ADC和△BOA中,
,
∴△ADC≌△BOA(AAS),
∴CD=OA=4,AD=OB=1,
∴OD=OA+AD=5,
∴C(﹣5,4);
(2)存在点E,使得|EC﹣EB|的值最大.
延长CB交x轴于E,
∵BC=|CE﹣EB|,BC>=|CE′﹣E′B|,
∴点E即为所求,
设直线CB的解析式为y=kx+b,
∵B(0,1),C(﹣5,4),
∴,
解得:,
∴直线CB的解析式为y=﹣x+1,
当y=0时,﹣x+1=0,解得:x=,
∴E(,0);
(3)如图,过点D作DF⊥y轴于F,延长FD交BP于G,
∵点A坐标(0,﹣6),点B坐标(8,0),
∴DF+DG=OB=8,
∵点D在直线y=﹣2x+2上,
∴设点D(m,﹣2m+2),
∴F(0,﹣2m+2),OF=|2m﹣2|,AF=|2m﹣2﹣6|=|2m﹣8|,
∵BP⊥x轴,B(8,0),
∴G(8,﹣2m+2),
同(1)的方法得,△AFD≌△DGP(AAS),
∴AF=DG,DF=PG,
∵DF+DG=DF+AF=8,
∴m+|2m﹣8|=8,
∴m=或m=0,
∴D(0,2)或(,﹣),
当m=0时,G(8,2),DF=0,
∴PG=0,
∴P(8,2),
当m=时,﹣2m+2=﹣2×+2=﹣,
∴G(8,﹣),DF=m=,
∴BG=,
∴P(8,),
即:D(0,2),P(8,2)或D(,﹣),P(8,).
2.(2020秋 济阳区期末)如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.
(1)求直线l2的解析式;
(2)点M在直线l1上,MN∥y轴,交直线l2于点N,若MN=AB,求点M的坐标.
(3)在x轴上是否存在点P,使以B、C、P为顶点的三角形是等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)把(1,m)代入y=x+3得m=4,
∴C(1,4),
设直线l2的解析式为y=kx+b,把C(1,4),A(3,0)代入得:
∴,解得,
∴直线l2的解析式为y=﹣2x+6;
(2)如图:
在y=x+3中,令y=0,得x=﹣3,
∴B(﹣3,0),
∴AB=3﹣(﹣3)=6,
设M(a,a+3),由MN∥y轴,得N(a,﹣2a+6),
MN=|a+3﹣(﹣2a+6)|=|3a﹣3|,
∵MN=AB,
∴|3a﹣3|=6,
解得a=3或a=﹣1,
∴M(3,6)或(﹣1,2);
(3)存在,设P(t,0),则CP2=(t﹣1)2+16,BP2=(t+3)2,
而BC2=(1+3)2+(4﹣0)2=32,
①当BP=CP时,如图:
∴(t+3)2=(t﹣1)2+16,
解得t=1,
∴P(1,0);
②当BC=BP时,如图:
∴(t+3)2=32,
解得t=﹣3+4或t=﹣3﹣4,
∴P(﹣3+4,0)或(﹣3﹣4,0),
③当BC=CP时,如图:
∴(t﹣1)2+16=32,
解得t=5或t=﹣3(与B重合,舍去),
∴P(5,0),
综上所述,P的坐标为:(1,0)或(﹣3+4,0)或(﹣3﹣4,0)或(5,0).
3.(2020秋 九江期末)如图,已知直线AB的解析式为y=x+m,线段CD所在直线解析式为y=﹣x+n,连接AD,点E为线段OA上一点,连接BE,使得∠EBO=2∠BAD.
(1)求证:△AOD≌△BOC;
(2)求证:BE=EC;
(3)当AD=10,BE=5时,求m与n的值.
【解答】(1)证明:在y=x+m中,令x=0,则y=m,令y=0,则x=﹣m,
∴A(﹣m,0),B(0,m),
∴OA=OB=m,
在y=﹣x+n中,令x=0,则y=n,令y=0,则x=n,
∴C(n,0),D(0,n),
∴OC=OD=n,
在△AOD与△BOC中,
,
∴△AOD≌△BOC(SAS);
(2)证明:由(1)知,OA=OB,OC=OD,∠AOB=∠COD=90°,
∴∠OAB=∠OBA=∠ODC=∠CDO=45°,
∵△AOD≌△BOC,
∴∠ADB=∠BCO,
∵∠ADO=∠ABO+∠BAD=45°+∠BAD,
∠BCO=∠DCO+∠BCD,
∴∠BAD=∠BCD,
设∠BAD=∠DCB=α,则∠EBO=2∠BAD=2α,
∴∠DBC=45°﹣α,
∵∠ECB=∠DCO+∠BCD=45°+α,
∠EBC=∠EBO+∠CBO=2α+45°﹣α=45°+α,
∴∠ECB=∠EBC,
∴BE=EC;
(3)解:由(1)知OA=OB=m,OC=OD=n,
∵∠AOD=∠BOE=90°,
∴AO2+OD2=AD2,OB2+OE2=BE2,
∵AD=10,BE=CE=5,
∴m2+n2=102,m2+(5﹣n)2=(5)2,
∴m=4,n=2.
4.(2021秋 兴化市月考)如图,在平面直角坐标系中,一次函数y=﹣x+b的图象与x轴,y轴分别交于B,C两点,与正比例函数y=x的图象交于点A,点A的横坐标为4.
(1)求A,B,C三点的坐标;
(2)若动点M在线段OA上运动,当三角形OMC的面积是三角形OAC的面积的时,求点M的坐标;
(3)若点P(m,1)在三角形AOB的内部(不包括边界),求m的取值范围.
【解答】解:(1)∵点A在正比例函数y=x的图象上,且点A的横坐标为4.
∴点A(4,2),
∵一次函数y=﹣x+b的图象与正比例函数y=x的图象交于点A,
∴2=﹣4+b,
∴b=6,
∴一次函数解析式为y=﹣x+6,
∵一次函数y=﹣x+6的图象与x轴,y轴分别交于B,C两点,
∴点B(6,0),点C(0,6);
(2)由(1)可知:OC=6,xA=4,
∴S△OAC=×OC×xA=×6×4=12,
∵S△OMC=S△OAC=4,
∴S△OMC=×OC×|xM|=4,
∴|xM|=,
∴xM=±,
当动点M在线段OA上时,x>0,则当x=时,y=×=,
∴此时M点的坐标为(,);
(3)∵点P(m,1)在△AOB的内部(不包括边界),
∴当y=1时,代入正比例函数中得:1=x,
解得:x=2,
当y=1时,代入一次函数中得:1=﹣x+6,
解得:x=5,
∴2<m<5.
故答案为:2<m<5.
5.(2021秋 市中区期中)如图1,在平面直角坐标系xOy中,O为坐标原点,直线AB:y=kx+3与直线AC:y=﹣2x+b交于点A(2,n),与x轴分别交于点B(﹣6,0)和点C.点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F.
(1)填空:k= ;n= 4 ;b= 8 ;
(2)求△ABC的面积;
(3)当点E落在y轴上时,求点E的坐标;
(4)若△DEF为直角三角形,求点D的坐标.
【解答】解:(1)把B(﹣6,0)代入kx+3,
∴﹣6k+3=0,
∴k=,
∴直线AB解析式:y=x+3,
把点A(2,n)代入y=x+3,
∴n=4,
∴A(2,4),
把(2,4)代入y=﹣2x+b得,
﹣4+b=4,
∴b=8,
故答案为:;4;8;
(2)∵直线AC:y=﹣2x+8,
∴点C(4,0),
∵点A(2,4),点B(﹣6,0)和点C(4,0),
∴BC=10,△ABC的BC边上的高为4,
∴S△ABC=×10×4=20;
(3)如图,过点A作AH⊥y轴于点H,
∴AH=2,AE2=AB2=(﹣6﹣2)2+42=80,
∴HE==2,
∴OE=HE﹣OH=2﹣4,
∴E点的坐标为(0,4﹣2);
(4)△DEF为直角三角形,分两种情况讨论:
当∠EDF=90°时,
如图,由对折可得,∠ADB=∠ADE==135°,
∴∠ADO=135°﹣90°=45°,
过点A作AG⊥BC于G,
∴AG=DG=4,
∵OG=2,
∴OD=2,
∴D(﹣2,0);
当∠DFE=90°时,
由对折得,AE=AB==4,BD=DE,
∴EF=4﹣4,
由A、B两点坐标可得:BF=2﹣(﹣6)=8,
设DF=m,则BD=8﹣m,
∴DE=8﹣m,
∴(8﹣m)2=m2+(4﹣4)2,
∴m=2﹣2,
∴OD=DF﹣OF=2﹣2﹣2=2﹣4,
∴D(4﹣2,0),
综上,D(﹣2,0)或(4﹣2,0).
6.(2021秋 三元区期中)如图,直线l:y=﹣x+3分别与x轴,y轴交于A,B两点,在OB上取一点C(0,2),以线段BC为直角边向右作等腰直角三角形BCD,△BCD沿直线CD的方向以每秒1个单位长度的速度向右匀速运动,设运动时间为t秒(t>0).
(1)求A,B两点的坐标;
(2)在△BCD运动的过程中,t为何值时,顶点D落在直线l上?请说明理由;
(3)在△BCD运动的过程中,是否存在实数t,使得DO+DA有最小值?若存在,求出t的值;若不存在,请说明理由.
【解答】解:(1)∵y=﹣x+3分别与x轴,y轴交于A,B两点,
∴当x=0时,y=3,当y=0时,x=6,
∴点A(6,0),点B(0,3);
(2)∵点C(0,2),点B(0,3),
∴BC=1,
∵△BCD是等腰直角三角形,
∴CD=BC=1,∠BCD=90°,
∴点D(1,2),
若顶点D落在直线l上,
∴当y=2时,则2=﹣x+3,
∴x=2,
∴t==1;
(3)如图,作点O关于直线CD的对称点O',连接O'A交直线CD于点D',此时,D'O+D'A有最小值;
∵点O与点O'关于直线CD对称,
∴O'(0,4),
设直线O'A的解析式为y=kx+4,
∴0=6k+4,
∴k=﹣,
∴直线O'A的解析式为y=﹣x+4,
当y=2时,2=﹣x+4,
∴x=3,
∴t==2,
当t=2时,使得DO+DA有最小值.
7.(2021秋 雨城区校级期中)如图,直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,若点E在线段AB上,OE⊥OF,且OE=OF,连接AF.
(1)直接写出点A,B的坐标,并求出线段AB的长.
(2)猜想线段AF与BE之间的数量与位置关系,并证明;
(3)过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=3,求CF的长.
【解答】解:(1)直线AB:y=x﹣4与x轴交于点A,与y轴交于点B,
令x=0,则y=﹣4,
∴B(0,﹣4),
∴OB=4,
令y=0,则x﹣4=0,
∴x=4,
∴A(4,0),
∴OA=4,
∴AB==4;
(2)猜想:AF=BE,AF⊥BE,
证明:∵OE⊥OF,OA⊥OB,
∴∠FOA=∠EOB,
∵点A(4,0),点B(0,﹣4),
∴OA=OB,
在△FOA和△EOB中,
,
∴△FOA≌△EOB(SAS),
∴AF=BE,∠FAO=∠EBO,
∵∠EBO+∠OAB=90°,
∴∠FAO+∠OAB=90°,即∠FAB=90°,
∴AF⊥BE,
∴AF=BE,AF⊥BE;
(3)连接CE,
∵OA=OB=4,AB=4,BE=3,
∴AF=BE=3,AE=,
∵OE=OF,OM⊥EF,
∴OM是线段EF的垂直平分线,
∴CF=CE,
设CF=x,则CE=x,AC=3﹣x,
在Rt△ACE中,CE2=AE2+AC2,即x2=()2+(3﹣x)2,
解得,x=,即CF=.
8.(2021秋 介休市期中)在“综合与探究”课上,张老师让每名同学在练习本上画出一个长方形,随后以该长方形为基本图形,以小组为单位编制一道综合探究题.经过思考和讨论,励志小组向全班同学分享了他们编拟的试题,得到了侯老师的认可,同学们也眼前一亮,纷纷动手,开始了探究.请你也跟他们一起来完成这道试题吧.如图1,分别以长方形OABC的边OC,OA所在直线为x轴、y轴,建立平面直角坐标系,已知AO=10,AB=6,点E在线段OC上,以直线AE为轴,把△OAE翻折,点O的对应点D恰好落在线段BC上.
(1)分别求点D,E的坐标.
(2)如图2,若直线AD与x轴相交于点F,求直线AD表达式及点F的坐标.
(3)在(2)的条件下,P是x轴上的一动点,是否存在以A,P,F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
(4)在本题的探究过程中,你感悟到哪些数学思想,请至少写出两条.
【解答】解:(1)如图1,由折叠得:AD=AO=10,OE=DE,
Rt△ABD中,AB=6,
∴BD===8,
∵OA=BC=10,
∴CD=10﹣8=2,
∴D(6,2),
设OE=x,则EC=6﹣x,
由勾股定理得:DE2=EC2+CD2,
∴x2=(6﹣x)2+22,
解得:x=,
∴E(,0);
(2)设AD的解析式为:y=kx+b,
把A(0,10)和D(6,2)代入得:
,
解得:,
∴AD的解析式为:y=﹣x+10,
当y=0时,﹣x+10=0,
∴x=,
∴F(,0);
(3)①当AP=AF时,
∵AO⊥x轴,F(,0),
∴OP=OF=,
∴P(﹣,0);
②当AF=FP时,
由勾股定理得:AF==,
∴OP′=﹣=5,OP=+=20,
∴P′(﹣5,0),P(20,0);
③当AP=FP时,
由勾股定理得:FP2=AP2=OP2+OA2,
∴(OP+)2=OP2+102,
解得:OP=,
∴P(﹣,0),
综上,点P的坐标为(﹣,0)或(﹣5,0)或(20,0)或(﹣,0);
(4)在本题的探究过程中,由(1)可知利用数形结合的思想,由(2)和(1)列方程可解答,利用了方程思想,由(3)运用了分类讨论的思想.
9.(2021秋 寿阳县期中)已知在平面直角坐标系中,直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),直线y1分别与x轴,y轴交于点A和点B.
(1)求直线y1与y2的表达式及点A,点B的坐标;
(2)x轴上是否存在点P,使△ACP的面积为30,若存在,求出点P的坐标;若不存在,说明理由;
(3)x轴上是否存在点Q,使△OCQ为等腰三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【解答】解:(1)∵直线y1=k1x+4(k1≠0)与直线y2=k2x(k2≠0)交于点C(6,12),
∴12=6k1+4,12=6k2,
解得:k1=,k2=2,
∴y1=x+4,y2=2x,
在y1=x+4中,当y1=0时,x=﹣3,
∴A(﹣3,0),
当x=0时,当y1=4,
∴B(0,4);
(2)存在,理由如下:
设P(m,0),
∵A(﹣3,0),C(6,12),
∴AP=|m+3|,
∵△ACP的面积为30,
∴×12×|m+3|=30
解得:m=2或﹣8,
∴P(2,0)或P(﹣8,0);
(3)∵点C(6,12),
∴OC===6,
当OC=OQ时,如图:
OC=OQ=6,
∵点Q的坐标为(﹣6,0)或(6,0);
当CO=CQ时,如图:作CD⊥x轴于D,
∵CO=CQ,
∴DQ=OD=6,
∴OQ=12,
∴点Q的坐标为(12,0);
当CQ=OQ时,如图:
∵CQ=OQ,CQ2=122+(OQ﹣6)2,
∴OQ2=122+(OQ﹣6)2,解得OQ=15,
∴点Q的坐标为(15,0).
综上所述,存在点Q,使△OCQ为等腰三角形,点Q的坐标为(﹣6,0)或(6,0)或(12,0)或(15,0).
10.(2021秋 通川区校级期中)如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B的坐标为(2,4),一次函数y=﹣x+b的图象与边OC、AB、x轴分别交于点D、E、F,∠DFO=30°,并且满足OD=BE,点M是线段DF上的一个动点.
(1)求b的值;
(2)连接OM,若△ODM的面积与四边形OAEM的面积之比为1:3,求点M的坐标;
(3)求OM+MF的最小值.
【解答】解:(1)y=﹣x+b中,令x=0,解得y=b,则点D的坐标是(0,b),OD=b,
∵OD=BE,
∴BE=b,
∵点B的坐标为(2,4),
∴点E的坐标为(2,4﹣b),
把E点坐标代入y=﹣x+b得4﹣b=﹣2+b,
解得b=3;
(2)∵b=3,点D的坐标是(0,b),点E的坐标为(2,4﹣b),
∴点D的坐标是(0,3),点E的坐标为(2,1),
∴OD=3,AE=1,OA=2,
∵S四边形OAED=(OD+AE) OA=×(3+1)×2=4,
∵△ODM的面积与四边形OAEM的面积之比为1:3,
∴△ODM的面积与四边形OAED的面积之比为1:4,
∴S△ODM=S四边形OAED=,
设点M的横坐标是a,则 3a=,解得a=,
把x=a=代入y=﹣x+3得y=﹣×+3=,
∴点M的坐标是(,);
(3)过点M作MN⊥x轴交于点N,
∵∠DFO=30°,
∴MN=MF,
∴OM+MF=OM+MN,
作点O关于一次函数的对称点O',过点O'作x轴的垂线交x轴于点N',交一次函数于点M′,
∴OM′=O′M′,
∴OM+MN的最小值=OM′+M′N′,
当O′、M′、N′在同一直线时,OM′+M′N′的值最小,为O'N',
∵∠DFO=30°,
∴∠ODF=60°,∠DOM=30°,∠O'ON'=90°﹣30°=60°,
在Rt△ODM中,OM=OD =3×=,
∴OO′=2OM=3,
在Rt△ON'O'中,
N'=OO′ =3×=.
∴OM+MF的最小值为.
11.(2021秋 深圳校级期中)如图所示,在平面直角坐标系中,直线y=x+1与y=﹣x+3分别交x轴于点B和点C,点D是直线y=﹣x+3与y轴的交点.
(1)求点B、C、D的坐标;
(2)设M(x,y)是直线y=x+1上一点,△BCM的面积为S,请写出S与x的函数关系式;来探究当点M运动到什么位置时,△BCM的面积为10,并说明理由.
(3)线段CD上是否存在点P,使△CBP为等腰三角形,如果存在,直接写出P点的坐标;如果不存在,请说明理由.
【解答】(1)解:把y=0代入y=x+1得:0=x+1,
∴x=﹣1,
∴B(﹣1,0),
当x=0时,y=﹣x+3=0,
∴D(0,3),
把y=0代入y=﹣x+3得:0=﹣x+3,
∴x=4,
∴C(4,0),
即B(﹣1,0),C(4,0),D(0,3);
(2)解:BC=4﹣(﹣1)=5,∵M(x,y)在y=x+1上,
∴M(x,x+1),
过M作MN⊥x轴于N,
①当M在x轴的上方时,MN=x+1,
∴S=BC MN=×5×(x+1)=x+;
②当M在x轴的下方时,MN=|x+1|=﹣x﹣1,
∴S=BC MN=×5×(﹣x﹣1)=﹣x﹣;
把S=10代入得:10=x+得:x=3,x+1=4;
把S=10代入y=﹣x﹣得:x=5=﹣5,x+1=﹣4;
∴M(3,4)或(﹣5,﹣4)时,s=10;
即S与x的函数关系式是,点M运动到(3,4)或(﹣5,﹣4)时,△BCM的面积为10;
(3)解:∵C(4,0),D(0,3),
∴OC=4,OD=3,
在Rt△OCD中,
由勾股定理得:CD===5,
有三种情况:
①CB=CP=5时,此时P与D重合,P的坐标是(0,3);
②BP=PC时,此时P在BC的垂直平分线上,P的横坐标是x==,
代入y=﹣x+3得:y=,
∴P的坐标是(,);
③BC=BP时,设P(x,﹣x+3),
根据勾股定理得:(x+1)2+(﹣x+3﹣0)2=52,
解得:x=﹣或x=4,
∵P在线段CD上,
∴x=﹣(舍去),
当x=4时,与C重合,(舍去);
∴存在点P,使△CBP为等腰三角形,P点的坐标是(0,3)或(,).
12.(2021秋 南岸区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4分别交x轴、y轴于点A、B,经过点B的直线y=﹣x+b交x轴于点C.
(1)求点C的坐标;
(2)动点P在射线AB上运动,过点P作PH⊥x轴,垂足为点H,交直线BC于点Q,设点P的横坐标为t.线段PQ的长为d(d≠0).求d关于t的函数解析式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,当点P在线段AB上时,连接CP,若S△CPQ=,在线段BC上取一点M.连接PM,使∠BPM+2∠ABO=90°,问在x轴上是否存在点R,使△PMR是以∠PMR为直角的直角三角形?若存在,请求出点R的坐标;若不存在,请说明理由.
【解答】解:(1)直线y=2x+4,当x=0时,y=4;
当y=0时,则2x+4=0,
解得x=﹣2,
∴A(﹣2,0),B(0,4),
∵直线y=﹣x+b经过点B(0,4),
∴b=4,
∴直线y=﹣x+b的解析式为y=﹣x+4,
当y=0时,则﹣x+4=0,
解得x=4,
∴C(4,0).
(2)∵PH⊥x轴于点H,交直线BC于点Q,且点P的横坐标为t,
∴P(t,2t+4),Q(t,﹣t+4),
如图1,点P在y轴的左侧,则﹣2≤t<0,
∵PQ=﹣t+4﹣(2t+4)=﹣3t,
∴d=﹣3t(﹣2≤t<0);
如图2,点P在y轴的右侧,则t>0,
∵PQ=2t+4﹣(﹣t+4)=3t,
∴d=3t(t>0),
综上所述,d关于t的函数解析式为.
(3)存在,
如图3,连接OP,PM交y轴于点F,∠PMR=90°,作PE⊥y轴于点E,
∵点P在线段AB上,且S△CPQ=,
∴×(﹣3t)(4﹣t)=,
整理得t=﹣1或t=5(不符合题意,舍去),
∴P(﹣1,2),E(0,2),
∴点P为AB的中点,
∵∠AOB=90°,
∴OP=AB=PB,
∴∠ABO=∠POB,
∴∠APO=∠ABO+∠POB=2∠ABO,
∵∠BPM+2∠ABO=90°,
∴∠BPM+∠APO=90°,
∴∠OPF=90°,
∵∠OEP=90°,OE=2,PE=1,
∴OP==,
∵S△POF=OF PE=PF OP,
∴PF=OF=OF=OF,
∵PF2+OP2=OF2,
∴(OF)2+()2=OF2,
解得OF=,
∴F(0,),
设直线PF的解析式为y=kx+,则﹣k+=2,
解得k=,
∴直线PF的解析式为y=x+,
由得,
∴M(1,3),
设直线OP的解析式为y=mx,则﹣m=2,
解得m=﹣2,
∴直线OP的解析式为y=﹣2x,
∵∠PMR+∠OPF=180°,
∴MR∥OP,
设直线MR的解析式为y=﹣2x+n,则﹣2+n=3,
解得n=5,
∴直线MR的解析式为y=﹣2x+5,
当y=0时,则﹣2x+5=0,
解得x=,
∴点R的坐标为(,0).
13.(2021秋 本溪期中)已知一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、B,与直线y=x相交于点C,过B作x轴的平行线l,点P是直线l上的一个动点.
(1)直接写出点A、B的坐标:A (8,0) 、B (0,6) .
(2)若S△AOC=S△BCP,求点P的坐标;
(3)若点E是平面内的一个动点,当△ABE是AB为直角边的等腰直角三角形,则点E的坐标为 (6,14)或(﹣6,﹣2)或(14,8)或(2,﹣8) .
【解答】解:(1)对于y=﹣x+6,
当x=0时,y=6;
当y=0时,则﹣x+6=0,解得x=8,
∴A(8,0),B(0,6).
(2)如图1,过点C作CD⊥x轴于点D,交直线l于点E,
由得,
∴C(3,),
∴D(3,0),E(3,6),
∴CD=,CE=6=,
设P(x,6),
∵S△AOC=S△BCP,且BP=|x|
∴×8×=×|x|,
解得x=或x=,
∴P(,6)或P′(,6),
∴点P的坐标为(,6)或(,6).
(3)如图2,EB=BA,且∠ABE=90°,点E在y轴右侧,
作EG⊥y轴于点G,则∠BGE=∠AOB=90°,
∴∠EBG=90°﹣∠ABO=∠BAO,
∴△BGE≌△AOB(ASA),
∴GB=OA=8,GE=OB=6,
∴OG=OB+GB=6+8=14,
∴E(6,14);
如图2,E′B=BA,且∠ABE′=90°,点E′在y轴左侧,
∵E′B=EB,
∴点E′与点E关于点B成中心对称,
∴E′(﹣6,﹣2);
如图3,AE=BA,且∠BAE=90°,点E在x轴上方,
作EH⊥x轴于点H,则∠EHA=∠AOB=90°,
∴∠EAH=90°﹣∠OAB=∠ABO,
∴△EHA≌△AOB(ASA),
∴HE=OA=8,HA=OB=6,
∴OH=OA+HA=8+6=14,
∴E(14,8);
如图3,AE′=BA,且∠BAE′=90°,点E′在x轴下方,
∵E′A=EA,
∴点E′与点E关于点A成中心对称,
∴E′(2,﹣8),
综上所述,点E的坐标为(6,14)或(﹣6,﹣2)或(14,8)或(2,﹣8).
14.(2021秋 金牛区校级期中)如图,A(4,0),B(0,4),直线y=x+1与x轴、y轴、直线AB分别交于点C、E、D.
(1)求直线BC的解析式及D点的坐标;
(2)求四边形OADE的面积;
(3)F是OA的中点,过点F作直线l,若l恰好将四边形OADE分成面积比为1:4的两部分,求直线l的解析式.
【解答】解:(1)∵直线y=x+1与x轴、y轴分别交于点C、E,
∴C(﹣2,0),E(0,1),
设直线BC的解析式为y=kx+b,
根据题意得,
解得,
∴直线BC的解析式为y=2x+4;
∵A(4,0),B(0,4),
设直线AB的解析式为y=ax+4,
∴4a+4=0,解得a=﹣1,
∴直线AB的解析式为y=﹣x+4,
∵直线y=x+1与线AB交于点D.
联立得,解得,
∴D(2,2);
(2)过点D作DH⊥x轴于H,
∵D(2,2),E(0,1),A(4,0),
∴DH=2,OH=2,OE=1,OA=4,AH=4﹣2=2,
∴S四边形OADE=S梯形OHDE+S△ADH=×2×(1+2)+×2×2=5;
(3)∵F是OA的中点,A(4,0),
∴F(2,0),
∴AF=OF=2,
设直线l与四边形OADE的另一交点为M,M的纵坐标为y,直线l恰好将四边形OADE分成面积比为1:4的两部分,即直线MF恰好将四边形OADE分成面积比为1:4的两部分,
分两种情况:
①当点M在点F右侧时,S△AMF:S五边形OFMDE=1:4,如图:
∵S四边形OADE=5,
∴S△AMF=1,
∴AF y=1,即×2y=1,解得y=1,
∵点M在直线AB:y=﹣x+4上,
∴1=﹣x+4,解得x=3,
∴点M(3,1),
由F,M两点坐标可求得直线FM的解析式为y=x﹣2,即直线l的解析式为y=x﹣2;
②当点M在点F右左侧时,S△OMF:S五边形MFADE=1:4,如图:
∵S四边形OADE=5,
∴S△OMF=1,
∴AF y=1,即×2y=1,解得y=1,
∴点M与点E重合,
∴点M(0,1),
由F,M两点坐标可求得直线FM的解析式为y=﹣x+1,即直线l的解析式为y=﹣x+1;
综上可知,直线l的解析式为y=x﹣2或y=﹣x+1.
15.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
【解答】(1)解:∵+(a﹣4)2=0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4,
则OA=OB=4.
∵AH⊥BC即∠AHC=90°,∠COB=90°,
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA);
(2)证明:过O分别作OM⊥CB于M点,作ON⊥HA于N点.
在四边形OMHN中,∠MON=360°﹣3×90°=90°,
∴∠COM=∠PON=90°﹣∠MOP.
∵△OAP≌△OBC,
∴OC=OP,
在△COM与△PON中,
,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=∠CHA=45°;
(3)证明:如图:连接OD.
∵∠AOB=90°,OA=OB,D为AB的中点,
∴OD⊥AB,∠BOD=∠AOD=45°,OD=DA=BD,
∴∠OAD=45°,∠MOD=90°+45°=135°,
∴∠DAN=135°=∠MOD.
∵MD⊥ND即∠MDN=90°,
∴∠MDO=∠NDA=90°﹣∠MDA.
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN.
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
16.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
【解答】解:(1)对于直线l2的解析式为y=﹣x+3,令x=0,得到y=3,
∴B(0,3),
令y=0,得到x=6,
∴A(6,0).
∴点A是坐标为(6,0),点B的坐标为(0,3);
(2)联立y=x,y=﹣x+3并解得:x=2,
∴点C(2,2),
∴S△COB=OB xC=×3×2=3;
(3)存在.
∵点B(0,3),点C(2,2),
∴BC==,
设P(0,y),
①当PC=BC=时,如图,
又∵点C(2,2),
∴PC2=22+(2﹣y)2,
∴()2=22+(2﹣y)2,
∴y=1或3,
∵y=3时,与点B重合,故舍去,
∴点P(0,1);
②当BP=BC=时,如图,
OP=OB+PB=3+,OP′=OB﹣P′B=3﹣,
∴点P(0,3+),(0,3﹣);
③当PB=PC时,如图,
∵PB2=PC2,
∴(3﹣y)2=22+(2﹣y)2,
∴解得:y=,
∴点P(0,),
综上所述:点P坐标为(0,3+),(0,3﹣),(0,1),(0,).
17.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
【解答】解:(1)当x=0时,y=﹣2k;当y=0时,x=2,
∴点B坐标为(0,﹣2k),点A坐标(2,0),
∴OA=2,OB=﹣2k,
∵OA=OB,
∴k=﹣1,
∴直线l的函数表达式为y=﹣x+2;
(2)在Rt△OAD中,AD=,OA=2,
∴OD==1,
∵∠OEB=∠ADO=∠AOB=90°,
∴∠BOE+∠OBE=90°,∠BOE+∠AOD=90°,
∴∠OBE=∠AOD,
∵OB=OA,
在Rt△OBE和Rt△AOD中,
,
∴△OBE≌△AOD(AAS),
∴BE=OD=1;
(3)点P始终在直线y=x上运动,
理由:如图3,过P作PE⊥x轴于E,PF⊥y轴于F,
则∠PFO=∠PEO=∠AOB=90°,
∴∠EPF=90°,
∵△ABP是等腰直角三角形,
∴∠APB=90°,PA=PB,
∴∠BPF=∠APE,
在△PBF与△PAE中,
,
∴△PBF≌△PAE(AAS),
∴PF=PE,
∴点P到x轴的距离等于点P到y轴的距离,
∴动点P在直线y=x(x>1)上运动.
18.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 A或B 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=|x+3|,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=|x+3﹣(﹣x+3)|=|x|,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=3,
∵PQ=BC,
∴|x|=3,解得:x=2或﹣2,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
19.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 (,6﹣) ,F的坐标为 (,2) ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 3或1 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 (0,8)或(0,2)或p(0,﹣2)或(0,) .
【解答】解:(1)∵正比例函数y=kx的图象过点C(2,4),
∴2k=4,
解得k=2,
∴正比例函数的表达式为y=2x;
∵一次函数y=﹣x+b的图象与正比例函数y=kx的图象交于点C(2,4),
∴4=﹣2+b,
∴b=6,
∴一次函数的表达式为:y=﹣x+6;
(2)∵点G在一次函数y=﹣x+6上,点F在正比例函数y=2x上,且点F.G.E在直线l上,E (m,0),m=,
∴点F、点G横坐标都为,
分别代入一次函数y=﹣x+6,正比例函数y=2x,
∴点G的纵坐标为y=﹣+6=6﹣,点F的纵坐标为y=2,
∴点G的坐标为(,6﹣),F的坐标为(,2),
∴FG=2﹣(6﹣)=3﹣6,
∴S△CFG=×(3﹣6)×(﹣2)=.
故答案为:(,6﹣),(,2),;
(3)①当点F在G点上方,即m>2时,
由(2)知点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=2m﹣(﹣m+6)=3m﹣6,
当GF=3时,3m﹣6=3,
解得:m=3;
②当F点在G点下方,即m<2时,
点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=(﹣m+6)﹣2m=﹣3m+6,
当GF=3时,﹣3m+6=3,
解得:m=1,
综上,m的值为3或1,
故答案为:3或1;
(4)①当CP=CO时,过点C作CM⊥y轴于M,△PCO为等腰三形,
∴PM=OM,
∵C(2,4),
∴OM=4.
∴PM=4,
∴P(0,8);
②当OP=OC时,
:C(2,4),
∴OC==2,
∴OP=2,
∴P(0,2)或p(0,﹣2);
③当PO=PC时,设P(0,y),
∴PO=|y|,PC==,
解得:y=,
∴P(0,).
故答案为:(0,8)或(0,2)或p(0,﹣2)或(0,).
20.(2021秋 和平区期中)已知,一次函数y=﹣x+6的图象与x轴、y轴分别交于点A、点B,与直线y=x相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.
(1)点A的坐标 (8,0) ,点B的坐标 (0,6) ;
(2)若S△AOC=S△BCP,求点P的坐标.
(3)若点E是直线y=x上的一个动点,当△APE是以AE为斜边的等腰直角三角形时,点E的坐标为 (,)或(16,20) .
(4)在(3)的条件下,当点P在AE右侧时,Q为平面内一点,EQ=2,连接OQ,将线段OQ绕着点O逆时针旋转90°,得到线段OM,连接QM,EM,直接写出EM的范围.
【解答】解:(1)在y=﹣x+6中,令y=0,
得﹣x+6=0,
解得:x=8,
∴A(8,0),
令x=0,得y=6,
∴B(0,6),
故答案为:(8,0),(0,6);
(2)由题意得:,
解得:,
∴C(3,),
∵直线l∥x轴,经过B(0,6),点P是直线l上的一个动点
∴P(x,6),
∴BP=|x|,
如图①,过点C作CG⊥OA于G,延长GC交BP于H,
则∠AGC=∠HGO=90°=∠BOG,
∵BP∥OA,
∴∠BHG=∠AGC=90°,
∴∠BHG=∠HGO=∠BOG=90°,
∴四边形BOGH是矩形,
∴GH=OB=6,
∵CG=,
∴CH=GH﹣CG=6﹣=,
∵S△AOC=S△BCP,
∴OA CG=BP CH,
即×8×= |x| ,
∴|x|=,
∴x=±,
∴P(,6)或(﹣,6);
(3)设点E(m,m)、点P(n,6),
∵△APE是以AE为斜边的等腰直角三角形,
∴PE=PA,∠APE=90°,
如图②,过点P作PF⊥OA于F,过点E作EK⊥PF于K,
则∠PKE=∠AFP=90°,
∴∠EPK+∠APF=90°,∠APF+∠PAF=90°,
∴∠EPK=∠PAF,
∴△PEK≌△APF(AAS),
∴EK=PF=6,PK=AF,
∵EK=|m﹣n|,PK=KF﹣PF=m﹣6,AF=|8﹣n|,
∴|m﹣n|=6,m﹣6=|8﹣n|,
解得:或,③
∴E(,)或(16,20);
(4)如图③,由(3)得E(,)或(16,20),
∵点P在AE右侧,
∴E(16,20),
∵EQ=2,
∴点Q在以E为圆心,半径为2的⊙E上运动,将OE绕点O逆时针旋转90°,得到ON,
以N为圆心,半径为2,作⊙N,连接EN交⊙N于M1,延长EN交⊙N于M2,
∵ON=OE==4,∠EON=90°,
∴EN=OE=4,
∵NM1=NM2=2,
∴EM的最小值为EM1=EN﹣NM1=4﹣2,
EM的最大值为EM2=EN+NM2=4+2,
∴EM的范围为4﹣2≤EM≤4+2.
21.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 y=﹣x+3 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 (﹣,) ;
②若△PQB的面积为,请直接写出点M的坐标 (,0)或(﹣,0) ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 (,0) .
【解答】解:(1)对于y=x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣x+3,
故答案为:y=﹣x+3;
(2)①设点M(m,0),
∴P(m,m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣,
∴P(﹣,),
故答案为:(﹣,);
②设点M(n,0),
∵点P在直线AB:y=x+3上,
∴P(n,n+3),
∵点Q在直线BC:y=﹣x+3上,
∴Q(n,﹣n+3),
∴PQ=|n+3﹣(﹣n+3)|=|n|,
∵△PQB的面积为,
∴S△PQB=|n| |n|=n2=,
∴n=±,
∴M(,0)或(﹣,0),
故答案为:(,0)或(﹣,0);
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,
∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,
∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,
∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,
∴EF=OK=,K(0,),
设F(x,0),则OE=x+,EH=OF=x,则H(x+,x),
∵C(6,0),K(0,),
设直线CK的解析式为y=kx+b,
∴,解得:,
∴直线CK的解析式为y=﹣x+,
∵点H在CK上,H(x+,x),
∴x=﹣(x+)+,解得:x=,
∴点F的坐标为(,0).
故答案为:(,0).
22.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 (1,7) .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组,得,
所以点C的坐标为(1,7),
故答案为:(1,7);
(2)∵M是直线AB上一点,
设点M的坐标为(a,a+6),
∵MN∥x轴,点N是直线y=﹣2x+9上一点,
∴a+6=﹣2x+9,解得x=,
∴点N的坐标是(,a+6),
∵MN=6,
∴|﹣a|=6,解得:a=5或﹣3,
∴点M的坐标为(5,11)或(﹣3,3);
(3)存在,
①点M的坐标为(﹣3,3)时,点N的坐标为(3,3),
∴MN=6,MC==,NC==,
设点P的坐标为(x,y),
∵直线y=x+6交x轴于点A,交y轴于点B,
∴B(0,6),OB=6=MN,
当BP=NC,OP=MC时;
,解得:或,
∴点P的坐标为(4,4)或(﹣4,4),
当BP=MC,OP=NC时,
,解得:或,
∴点P的坐标为(4,2)或(﹣4,2),
②点M的坐标为(5,11)时,点N的坐标为(﹣1,11),
∴MN=6,MC==,NC==,
此时△MNC与①中的△MNC三边都对应相等,所以此时情况与①相同.
综上,点P的坐标为(4,4)或(﹣4,4)或(4,2)或(﹣4,2).
23.(2021秋 龙华区校级期中)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线DE经过点C,过A作AD⊥DE于点D.过B作BE⊥DE于点E,则△BEC≌△CDA,我们称这种全等模型为“k型全等”.(不需要证明)
【模型应用】若一次函数y=kx+4(k≠0)的图象与x轴、y轴分别交于A、B两点.
(1)如图2,当k=﹣1时,若点B到经过原点的直线l的距离BE的长为3,求点A到直线l的距离AD的长;
(2)如图3,当k=﹣时,点M在第一象限内,若△ABM是等腰直角三角形,求点M的坐标;
(3)当k的取值变化时,点A随之在x轴上运动,将线段AB绕点B逆时针旋转90°得到BQ,连接OQ,则OQ长的最小值是 4 .
【解答】解:(1)由题意知△BEO≌△AOD,
∴OE=AD,
∵k=﹣1,
∴y=﹣x+4,
∴B(0,4),
∴OB=4,
∵BE=3,
∴OE=,
∴;
(2)当k=﹣时,y=﹣,
∴当x=3时,y=0,
∴A(3,0),
①当BM⊥AB,且BM=AB时,
过点M作MN⊥y轴,
∴△BMN≌△ABO(AAS),
∴MN=OB,BN=OA,
∴MN=4,BN=3,
∴M(4,7);
②当AB⊥AM,且AM=AB时,
过点M作x轴垂线MK,
∴△ABO≌△AMK(AAS),
∴OB=AK,OA=MK,
∴AK=4,MK=3,
∴M(7,3);
③当AM⊥BM,且AM=BM时,
过点M作MH⊥x轴,MG⊥y轴,
∴△BMG≌△AHM(AAS),
∴BG=AH,GM=MH,
∴4﹣MH=MH﹣3,
∴MH=,
∴M();
综上所述:M(7,3)或(4,7)或();
(3)如图,将线段OB绕点B逆时针旋转90°得BE,连接EQ,
∴∠ABO=∠EBQ,
又∵AB=BQ,OB=BE,
∴△ABO≌△QBE(SAS),
∴∠BEQ=∠BOA=90°,
∴点Q在直线x=4上运动,
∴OQ的最小值为4,
故答案为:4.
24.(2021秋 南海区期中)如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)求△ABC的面积.
(2)P为线段AB(不含A,B两点)上一动点.
①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.
【解答】解:(1)把A(4,0)代入得:m=3,
一次函数解析式为,
令x=0,得y=3,
∴B(0,3),
在Rt△AOB中,AB2=OA2+OB2,
∴AB=5,
∵BC=AB=5,
∴C(0,﹣2),
∴;
(2)①设,
∴P在线段AB上,
∴0<t<4,
设直线AC的解析式为y=kx+b,代入A(4,0),C(0,﹣2)得,
∴,
∴,
又∵PQ∥y轴,则,
∴,
∴S四边形APOQ=S△AOP+S△AOQ=AO×|yP|+AO×|yQ|=×4×PQ=×4×(5﹣t)=,
又∵,
∴,解得t=1;
②如图所示,当N点在x轴下方时,
∵BP=AM,
∴BP+AP=AM+AP=AB,
∴PM=AB=5,
∵△PMN是以PM为直角边的等腰直角三角形,
当∠NPM=90°时,PN=PM=5,,
设,
过P点作直线M'N'∥x轴,作MM'⊥M'N',NN'⊥M'N',
∴MM'∥OB,
∴∠ABO=∠PMM',
在△AOB与△PM'M中,
,
∴△AOB≌△PM'M(AAS),
∴MM'=OB=3,PM'=OA=4,
∵∠NPN'+∠MPM'=90°,∠NPN'+∠N'NP=90°,
∴∠MPM'=∠N'NP,
在△PNN'与△MPM'中,
,
∴△PNN'≌△MPM'(AAS),
∴PN'=MM'=3,NN'=PM'=4,
∴M'N'=7,作MH⊥NN',则NH=1,
∵,
∴,
∴M在直线AB上,
∴,
,
,
a=﹣1,
∴,
∴.
当N点在x轴上方时,点N'与关于A(4,0)对称,
则,即,
综上:存在一点或使△PMN是以PM为直角边的等腰直角三角形.
25.(2021秋 龙岗区校级期中)如图,一次函数y=﹣x+4的图象与x轴和y轴分别交于点A和B,再将△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 (8,0) ,点B的坐标为 (0,4) ;
(2)求直线CD的函数解析式;
(3)在直线AB上,是否存在点P,使得S△POD=S△OCD,若存在,请直接写出点P的坐标;若不存在,说明理由.
【解答】解:(1)令x=0,则y=4,
∴B(0,4),
令y=0,则0=﹣x+4,
∴x=8,
∴A(8,0),
故答案为:(8,0),(0,4);
(2)设OC=a,则AC=8﹣a,
由折叠知,BC=AC=8﹣a,
在Rt△BOC中,OB=4,
根据勾股定理得,BC2﹣OC2=OB2,
∴(8﹣a)2﹣a2=16,
∴a=3,
即:OC=3,
∴C(3,0),
∵△AOB沿直线CD对折,使点A与点B重合,直线CD与x轴交于点C,与AB交于点D.
A(8,0),B(0,4),
∴D(4,2),
设CD的函数解析式为:y=kx+b,
则,
解得,
∴直线CD的函数解析式为:y=2x﹣6;
(3)点P在OD下方时,过点C作OD的平行线交AB于P,
∵D(4,2),
∴直线OD的解析式为:y=x,
∴设直线CP的函数解析式为:y=x+b,将C(3,0)代入得:b=﹣,
∴直线CP的函数解析式为:y=,
∴=﹣x+4,
解得x=,
∴y=,
∴点P(),
当点P在OD上方时,则点D为PP'的中点,
∴P'(,),
综上:点P()或(,).
26.(2021 古冶区一模)如图,直角坐标系xOy中,过点A(6,0)的直线l1与直线l2:y=kx﹣1相交于点C(4,2),直线l2与x轴交于点B.
(1)k的值为 ;
(2)求l1的函数表达式和S△ABC的值;
(3)直线y=a与直线l1和直线l2分别交于点M,N,(M,N不同)
①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以MN为边作正方形MNDE,边DE恰好在x轴上,直接写出此时a的值.
【解答】解:(1)将点C(4,2)代入y=kx﹣1得,
2=4k﹣1,
解得,
故答案为:;
(2)设直线l1的表达式为y=k1x+b
将点A(6,0),C(4,2)代入得,
,
解得,
∴直线l1的表达式为y=﹣x+6,
当y=0时,,
解得x=,
∴点B的坐标为(,0),
∴AB=6﹣=,
∴S△ABC=;
(3)①当x=0时,y=x﹣1=﹣1,
y=﹣x+6=6,
∴M,N都在y轴右侧时a的取值范围是:﹣1<a<6且a≠2.
②当y=a时,x﹣1=a,则x=,
∴点N的坐标为(,a),
当y=a时,﹣x+6=a,则x=6﹣a,
∴点M的坐标为(6﹣a,a)
∴MN=|6﹣a﹣|=||,
∵四边形MNDE为正方形,
∴||=|a|,
解得:或,
∴或.
27.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点D在l2上.
(1)①直接写出点C的坐标为 (2,1) ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
【解答】解(1)①∵y=kx﹣2k+1经过定点C,
∴点C的坐标与k的取值无关,
∴x=2时,y=1,
∴C(2,1),
故答案为:(2,1);
②设l2的解析式为:y=ax,
把C(2,1)代入y=ax得:a=,
∴l2的解析式为y=,
(2)如图,取OB的中点H,连接CH,
∵C(2,1),
∵S△BOC=2S△BCD,
当点D在线段OC上时,
则点D为OC的中点,
∴D(1,);
当点D在线段DC的延长线时,
∴S△BCD=,
即OB=,|xD|=3,
∴D(3,),
综上所述,符合条件的点D坐标为(1,)或(3,).
(3)过点C作CH∥EF,过点O作OH⊥OC,分别过点C,H作CM⊥OB于M,MN⊥OB于N,
∵∠EDO=45°,
∴∠OCH=45°,
∴OC=OH,
又∵∠MOC=∠NHO,∠OMC=∠ONH,
∴△COM≌△OHN(AAS),
∴CM=OH,OM=NH,
由C(2,1)得:H(1,﹣2),
∴yCH=3x﹣5,
由E(0,﹣)得:yEF=3x﹣,
∴P(,0),
过点F作FK⊥OA于K,
∵PF=PE,
∴△OPE≌△FPK(AAS),
∴F(1,),
将F(1,)代入l1:y=kx﹣2k+1,
∴k﹣2k+1=,
解得k=﹣.
28.(2021春 任城区校级期末)如图,在平面直角坐标系中,直线AB与x轴、y轴相交于A(6,0)、B(0,2)两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.
(1)求证:△BOC≌△CED;
(2)求经过A、B两点的一次函数表达式及点D的坐标;
(3)在x轴上是否存在点P,使得以C、D、P为顶点的三角形是等腰三角形?若存在,请直接写出P点的坐标.(不用写过程)
【解答】解:(1)∵∠BOC=∠BCD=∠CED=90°,
∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,
∴∠BCO=∠CDE,
在△BOC与△CED中,
,
∴Rt△BOC≌Rt△CED(AAS);
(2)设直线AB解析式为y=kx+b,把A(6,0),B(0,2)代入上式得:,
解得,
故直线AB的解析式为,
∵△BOC≌△CED,
∴CO=DE,
设CO=DE=m,而OB=CE=2,
∴D(m+2,m),
∵点D在直线上,把D(m+2,m)代入上式并解得m=1,
∴D(3,1),
(3)存在,理由如下:
设点P的坐标为(t,0),
而点C,D的坐标分别为(1,0),(3,1),
由点P,C,D的坐标得:PC2=(t﹣1)2,PD2=(t﹣3)2+1,CD2=22+1=5,
当PC=PD时,则(t﹣1)2=(t﹣3)2+1,
解得:t=,
当PC=CD时,则(t﹣1)2=5,
解得:t=,
当PD=CD时,则(t﹣3)2+1=5,
解得:t=5或t=1(舍去),
故P的坐标为或或或(5,0).
29.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
【解答】解:(1)∵直线y=﹣x+b(b>0)平分矩形OABC的面积,
∴直线过矩形的中心,
∵B(12,6),
∴矩形中心为(6,3),
∴﹣6+b=3,
解得b=12;
(2)如图,假设存在ON平分∠CNM的情况,
当PM与线段BC,OA交于N,M时,
过点O作OH⊥MN于H,
∵ON平分∠CNM,OC⊥BC,OH⊥MN,
∴OH=OC=6,
∵OP=12,
∴∠OPN=30°,
∴OM=OP =4,
当y=0时,﹣,解得x=8,
∴OD=8,
∴DM=OD﹣OM=8﹣4;
当PM与直线BC,OA交于N,M时,如图,
同理可得,此时DM=OD+OM=8+4,
综上:存在ON平分∠CNM的情况,此时DM=8﹣4或8+4;
(3)设平移后的直线y=﹣与y轴交于点P',沿此直线折叠,点O的对应点恰好落在BC边上F处,连接P'F,OF,
则有OP'=P'F=m,CP'=m﹣6,
在Rt△CP'F中,由勾股定理得:
(m﹣6)2+92=m2,
解得m=,
∴PP'=12﹣=,
∴a=.
30.(2021春 渝中区校级期末)如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC:y=x交于点C.
(1)若直线AB解析式为y=﹣2x+12,求:
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值及此时点P的坐标;若不存在,说明理由.
【解答】解:(1)如图1,
①联立方程组得,
解得,
∴点C的坐标为(4,4);
②在y=﹣2x+12中,当x=0时y=12,
当y=0时,﹣2x+12=0,解得x=6,
∴点B(0,12),A(6,0),
则△OAC的面积为×6×4=12;
(2)由题意,在OC上截取OM=OP,连接MQ,
∵ON平分∠AOC,
∴∠AOQ=∠COQ,
又OQ=OQ.
∴△POQ≌△MOQ(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小,
即AQ+PQ存在最小值;
∵AB⊥ON,
∴∠AEO=∠CEO,
..△AEO≌△CEO(ASA),
∴OC=OA=4,
在Rt△OAM中,∵∠AOM=45°,
∴OM=AM=OA=2.
此时OP=OM=2,故P(2,0)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
