八年级数学12.2.1作轴对称图形(2)
文档属性
| 名称 | 八年级数学12.2.1作轴对称图形(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 347.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-06 00:00:00 | ||
图片预览



文档简介
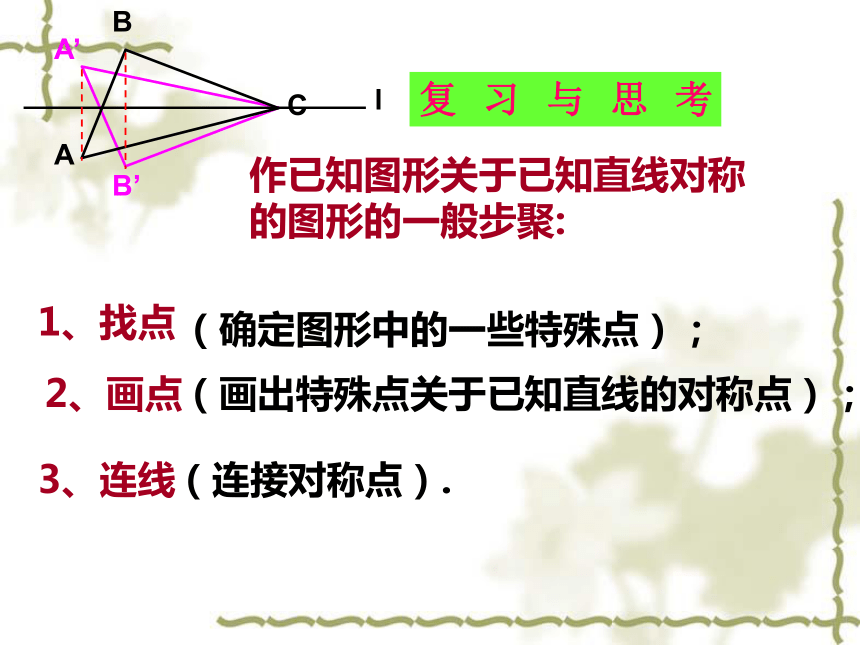
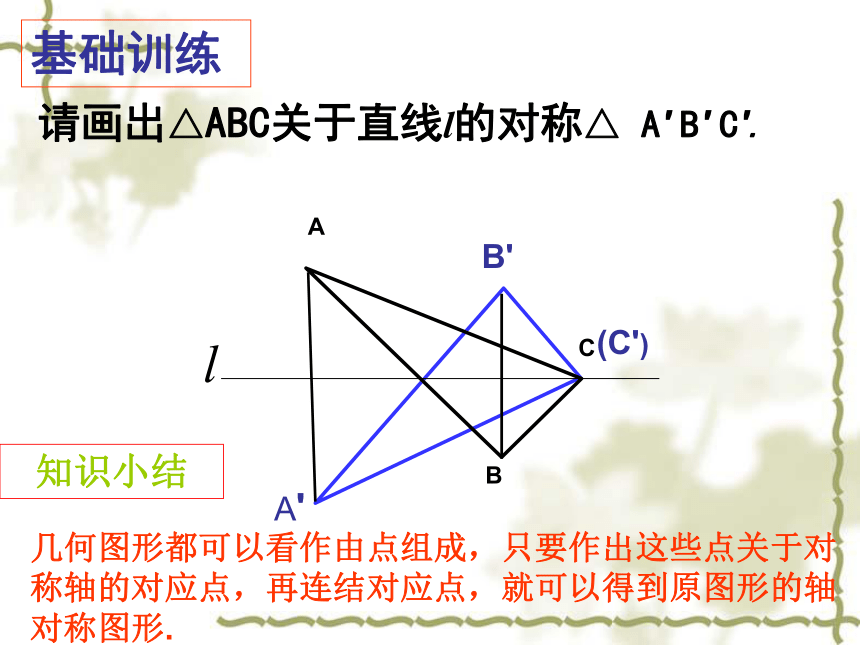
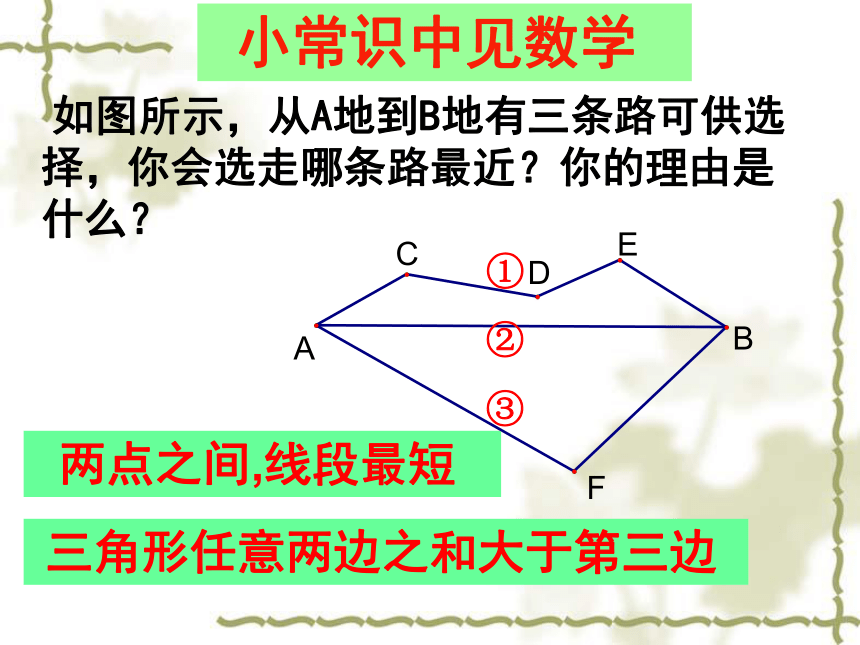
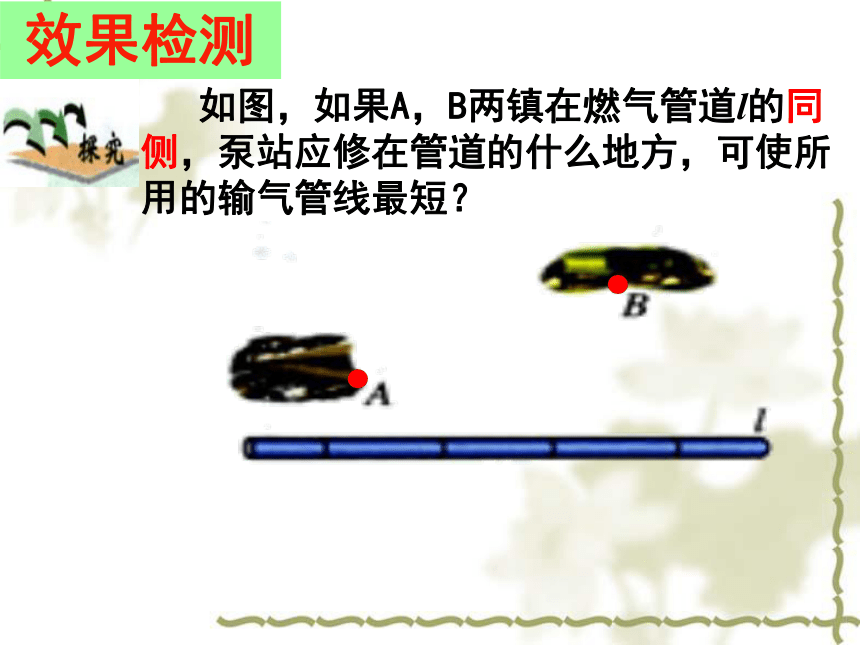
课件24张PPT。12.2.1 作轴对称图形(2)岳麓区坪塘中学C175作已知图形关于已知直线对称的图形的一般步聚:1、找点2、画点3、连线(确定图形中的一些特殊点);(画出特殊点关于已知直线的对称点);(连接对称点).复习与思考基础训练请画出△ABC关于直线l的对称△ A' B' C'.A'B'(C')几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连结对应点,就可以得到原图形的轴对称图形.知识小结 如图所示,从A地到B地有三条路可供选择,你会选走哪条路最近?你的理由是什么? 两点之间,线段最短 小常识中见数学 三角形任意两边之和大于第三边 如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
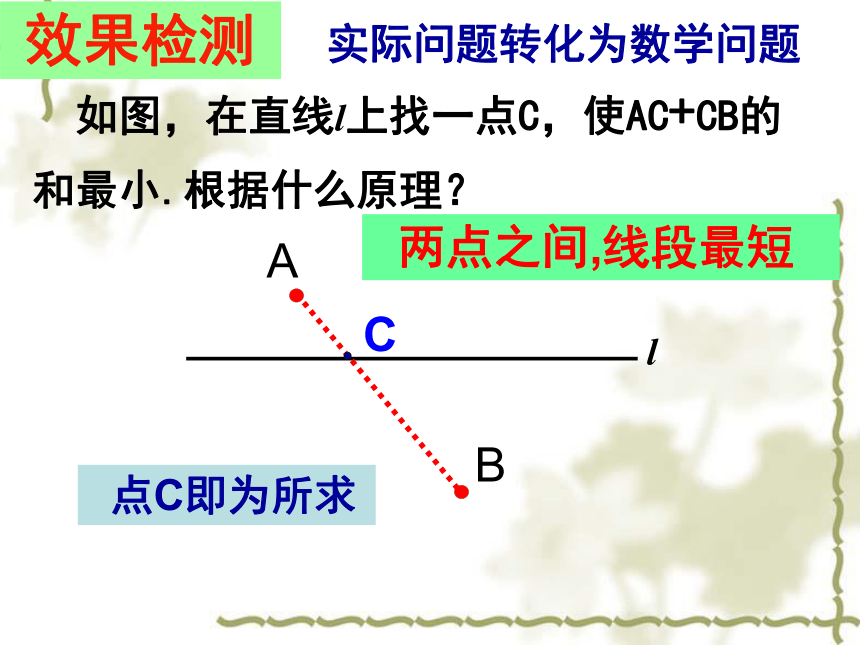
效果检测 实际问题转化为数学问题
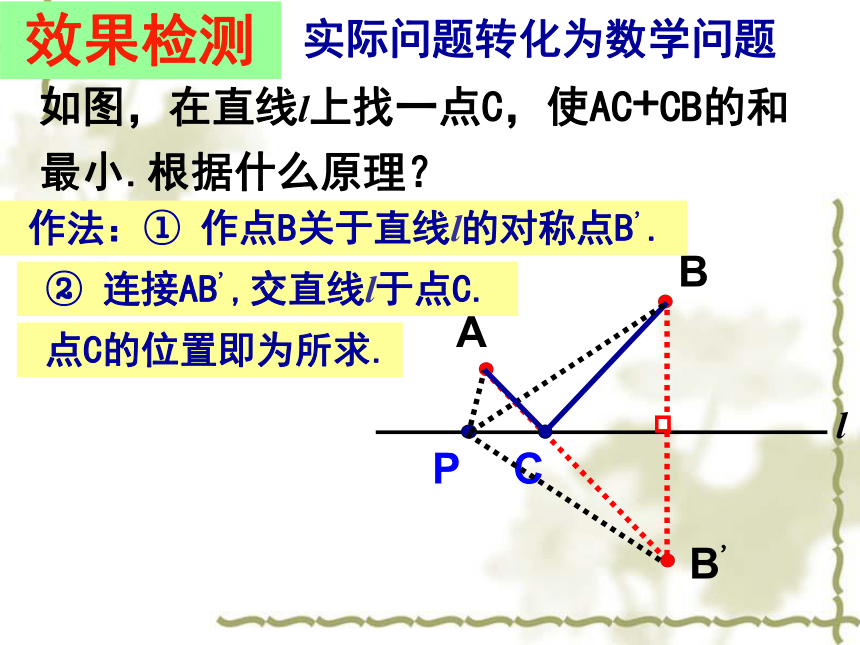
两点之间,线段最短 点C即为所求效果检测 如图,在直线l上找一点C,使AC+CB的
和最小.根据什么原理?
如图,如果A,B两镇在燃气管道l的同侧,泵站应修在管道的什么地方,可使所用的输气管线最短?效果检测 实际问题转化为数学问题效果检测 点C的位置即为所求.如图,在直线l上找一点C,使AC+CB的和最小.根据什么原理?
作法:① 作点B关于直线l的对称点B'. ② 连接AB',交直线l于点C.∵直线l是点B 、B'点的对称轴,P 、C在对称轴上,∴BP=B'P, BC=B'C在l上任取另一点C连结AC 、BC、B'C证明:在△AB'C中,AB'(1) 若要使厂部到A 村与B村的距离相
等则应如何选择厂址?
(2)若要使厂部到A 村与B村的水管用料
最省,则应如何选择厂址?拓 展 与 思 考 水泵站修在什么地方?如图所示,水泵站修在 C 点可使所用的水管最短. 如图,要在河边修建一个水泵站,分别向张村、李庄送水,修在河边什么地方,可使所用的水管最短?张村李庄A’C应用新知 效果检测 还有不同的方法找点C吗?在直线l上找一点C,使AC+CB的和最小.
1.八年级某班同学做游戏,在活动区域边放了一些球,则B处的小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处?P当堂训练BA′如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B.C2.已知,P,Q为△ABC的边AB,AC的两定点,在BC上求作一点M,使△PQM的周长最短.效果检测当堂训练M 点M即为所求. 如图,A是∠MON内一点,分别在OM、ON上作出点P、Q,使△APQ的周长最小.当堂训练例题讲解A1A2PQ例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近.
ABMNP1P2根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短.例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等.
ABMNP3根据:线段的垂直平分线上的点到这条线段两个端点的距离相等.
例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短.
ABMNP4根据:两点之间线段最短.又问:若村庄M,N在公路AB的同侧,则又如何解决此题?N1P5答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短.
1.如图,某地由于居民增多,要在公路边增加一个公共汽车站,A、B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?c解:
(1)连接AB,
(2)作AB的垂直平分 线交公路于点C.
则点C为车站地址. 这时有AC=BC.心动不如行动 2.为解决农民工子女上学难的问题,某市计划在新开发的A、B、C三个工业园新建一所农民工子弟学校.请你在图上找一点D,使点D到三个工业园距离相等.思考:三角形两边的中垂线交点也在第三边的中垂线上吗?作业讲评1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?P342.如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?AMBC作业讲评 如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷.请你帮助他确定这一天的最短路线.课本第47页第9题
效果检测 实际问题转化为数学问题
两点之间,线段最短 点C即为所求效果检测 如图,在直线l上找一点C,使AC+CB的
和最小.根据什么原理?
如图,如果A,B两镇在燃气管道l的同侧,泵站应修在管道的什么地方,可使所用的输气管线最短?效果检测 实际问题转化为数学问题效果检测 点C的位置即为所求.如图,在直线l上找一点C,使AC+CB的和最小.根据什么原理?
作法:① 作点B关于直线l的对称点B'. ② 连接AB',交直线l于点C.∵直线l是点B 、B'点的对称轴,P 、C在对称轴上,∴BP=B'P, BC=B'C在l上任取另一点C连结AC 、BC、B'C证明:在△AB'C中,AB'
等则应如何选择厂址?
(2)若要使厂部到A 村与B村的水管用料
最省,则应如何选择厂址?拓 展 与 思 考 水泵站修在什么地方?如图所示,水泵站修在 C 点可使所用的水管最短. 如图,要在河边修建一个水泵站,分别向张村、李庄送水,修在河边什么地方,可使所用的水管最短?张村李庄A’C应用新知 效果检测 还有不同的方法找点C吗?在直线l上找一点C,使AC+CB的和最小.
1.八年级某班同学做游戏,在活动区域边放了一些球,则B处的小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A处?P当堂训练BA′如图,EFGH是矩形的台球桌面,有两球分别位于A、B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF反弹后再击中B球?试一试:解:1.作点A关于EF的对称点A′ 2.连结A′B交EF于点C则沿AC撞击黑球A,必沿CB反弹击中白球B.C2.已知,P,Q为△ABC的边AB,AC的两定点,在BC上求作一点M,使△PQM的周长最短.效果检测当堂训练M 点M即为所求. 如图,A是∠MON内一点,分别在OM、ON上作出点P、Q,使△APQ的周长最小.当堂训练例题讲解A1A2PQ例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(1)当汽车行驶到什么位置时距村庄M最近?行驶到什么位置时距村庄N最近?答:如图 ,当汽车行驶到P1时,距村庄M最近,
当汽车行驶到P2时,距村庄N最近.
ABMNP1P2根据:直线外一点与直线上各点连结的所有线段中,
垂线段最短.例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(2)当汽车行驶到什么位置时,与村庄M、N的距离相等?
答:如图 ,当汽车行驶到P3时,与村庄M、N的距离相等.
ABMNP3根据:线段的垂直平分线上的点到这条线段两个端点的距离相等.
例 已知如图:一辆汽车在直线公路AB上由A向B行驶,M、N分别表示位于公路AB两侧的村庄,(3)当汽车行驶到什么位置时,到村庄M、N的距离之和最短?
答:如图 ,当汽车行驶到P4时,到村庄M、N的距离之和最短.
ABMNP4根据:两点之间线段最短.又问:若村庄M,N在公路AB的同侧,则又如何解决此题?N1P5答:若村庄M,N在公路AB的同侧时,当汽车行驶到P5时,到村庄M、N的距离之和最短.
1.如图,某地由于居民增多,要在公路边增加一个公共汽车站,A、B是路边两个新建小区,这个公共汽车站建在什么位置,能使两个小区到车站的路程一样长?c解:
(1)连接AB,
(2)作AB的垂直平分 线交公路于点C.
则点C为车站地址. 这时有AC=BC.心动不如行动 2.为解决农民工子女上学难的问题,某市计划在新开发的A、B、C三个工业园新建一所农民工子弟学校.请你在图上找一点D,使点D到三个工业园距离相等.思考:三角形两边的中垂线交点也在第三边的中垂线上吗?作业讲评1.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?P342.如图:AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?AMBC作业讲评 如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷.请你帮助他确定这一天的最短路线.课本第47页第9题
