八年级数学《等腰三角形的性质》课件
文档属性
| 名称 | 八年级数学《等腰三角形的性质》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 46.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-06 18:32:34 | ||
图片预览

文档简介
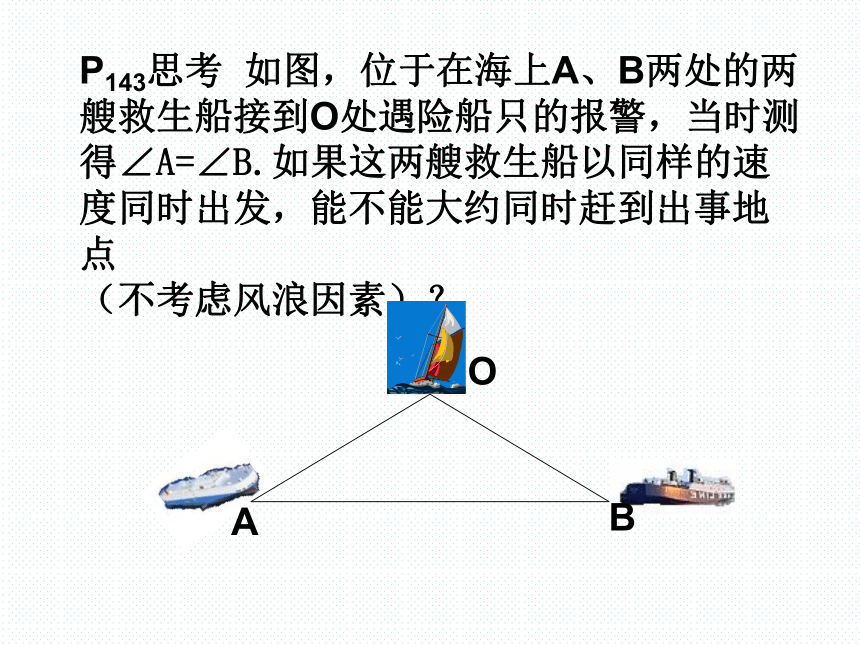
课件10张PPT。等腰三角形的判定P143思考 如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点
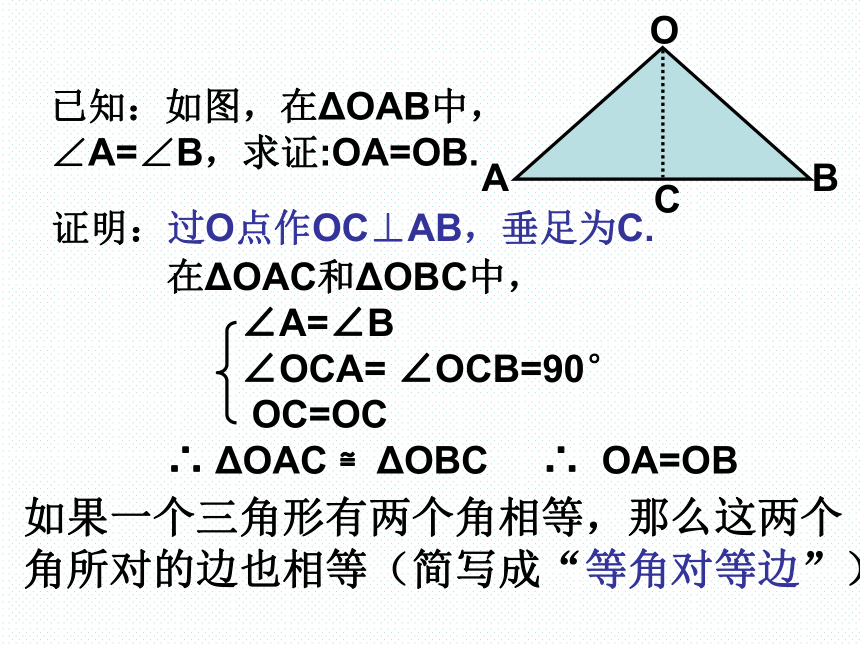
(不考虑风浪因素)?OBA已知:如图,在ΔOAB中,∠A=∠B,求证:OA=OB.证明:过O点作OC⊥AB,垂足为C.如果一个三角形有两个角相等,那么这两个
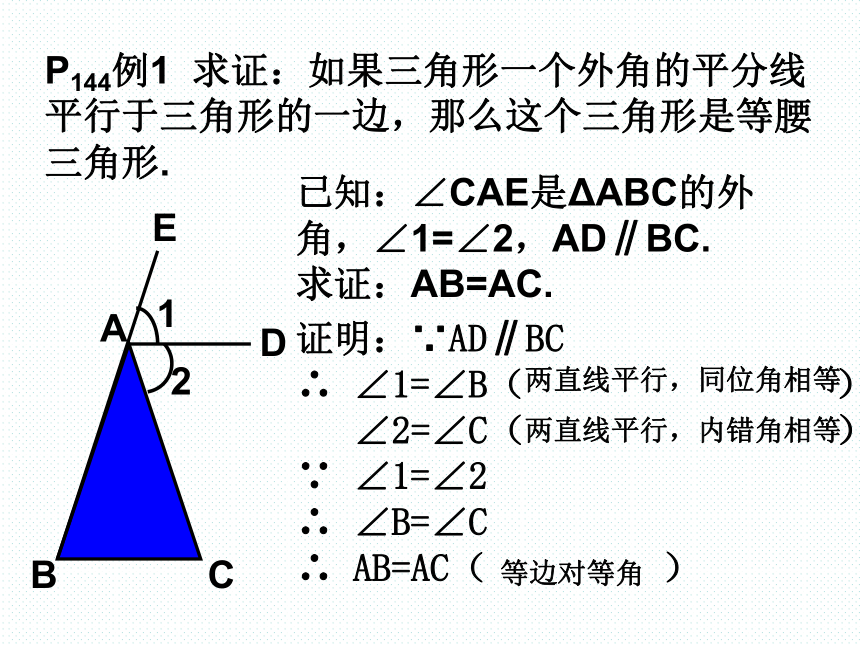
角所对的边也相等(简写成“等角对等边”).P144例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:∠CAE是ΔABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.证明:∵AD∥BC
∴ ∠1=∠B( )
∠2=∠C( )
∵ ∠1=∠2
∴ ∠B=∠C
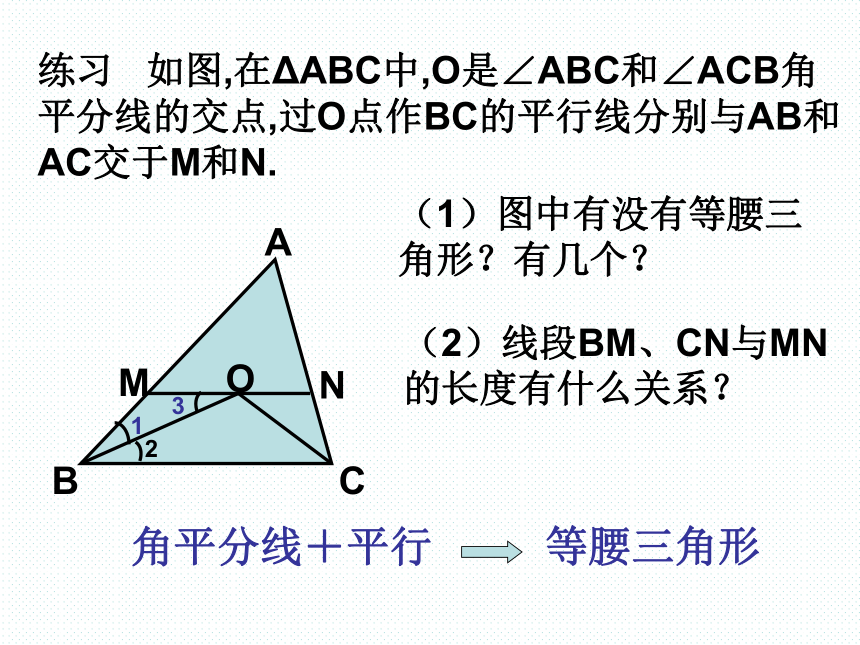
∴ AB=AC( )两直线平行,同位角相等两直线平行,内错角相等等边对等角练习 如图,在ΔABC中,O是∠ABC和∠ACB角
平分线的交点,过O点作BC的平行线分别与AB和
AC交于M和N.(1)图中有没有等腰三
角形?有几个?(2)线段BM、CN与MN
的长度有什么关系?课堂练习
P1451.如图,∠A=36°,∠DBC=36°,∠C=72°.
分别计算∠1、∠2的度数,并说明图中有哪些
等腰三角形.解:∠ABC=180°-∠A-∠C
=180°-36°-72°
=72°
∴ ∠2=∠ABC-∠DBC
=72°-36°
=36°
∴∠1=∠A+∠2=36°+36°
=72°P1452如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?P1453 如图,AC和BD相交于点O,且
AB∥DC,OA=OB,求证:OC=OD.证明:∵AB∥DC
∴∠A=∠C ∠B=∠D又∵OA=OB
∴∠A=∠B(等边对等角)思考题1如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?思考题2如图,∠B=∠E, ∠C=∠D,BC=DE,
F为CD的中点,求证:AF⊥CD.ABCDEF
(不考虑风浪因素)?OBA已知:如图,在ΔOAB中,∠A=∠B,求证:OA=OB.证明:过O点作OC⊥AB,垂足为C.如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”).P144例1 求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.已知:∠CAE是ΔABC的外角,∠1=∠2,AD∥BC.
求证:AB=AC.证明:∵AD∥BC
∴ ∠1=∠B( )
∠2=∠C( )
∵ ∠1=∠2
∴ ∠B=∠C
∴ AB=AC( )两直线平行,同位角相等两直线平行,内错角相等等边对等角练习 如图,在ΔABC中,O是∠ABC和∠ACB角
平分线的交点,过O点作BC的平行线分别与AB和
AC交于M和N.(1)图中有没有等腰三
角形?有几个?(2)线段BM、CN与MN
的长度有什么关系?课堂练习
P1451.如图,∠A=36°,∠DBC=36°,∠C=72°.
分别计算∠1、∠2的度数,并说明图中有哪些
等腰三角形.解:∠ABC=180°-∠A-∠C
=180°-36°-72°
=72°
∴ ∠2=∠ABC-∠DBC
=72°-36°
=36°
∴∠1=∠A+∠2=36°+36°
=72°P1452如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?P1453 如图,AC和BD相交于点O,且
AB∥DC,OA=OB,求证:OC=OD.证明:∵AB∥DC
∴∠A=∠C ∠B=∠D又∵OA=OB
∴∠A=∠B(等边对等角)思考题1如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?思考题2如图,∠B=∠E, ∠C=∠D,BC=DE,
F为CD的中点,求证:AF⊥CD.ABCDEF
