人教版八年级上册第十二章 轴对称>>作轴对称图形
文档属性
| 名称 | 人教版八年级上册第十二章 轴对称>>作轴对称图形 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-06 00:00:00 | ||
图片预览








文档简介
课件30张PPT。请欣赏下列几幅图片请欣赏下列几幅图片请欣赏下列几幅图片请欣赏下列几幅图片你知道这些美丽的图案是怎样得到的吗?人教版数学八年级(上)作轴对称图形兖州十四中12.2.1冯福泰学习目标:1.通过探索简单图形之间的轴对称关系,理
解轴对称变换的特征.3.认识和欣赏轴对称在现实生活中的应用,能
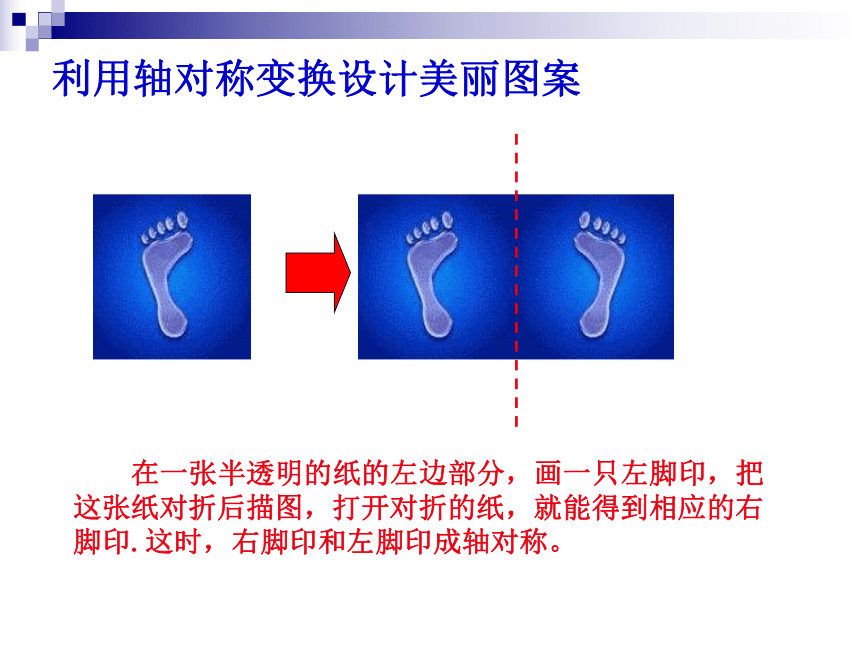
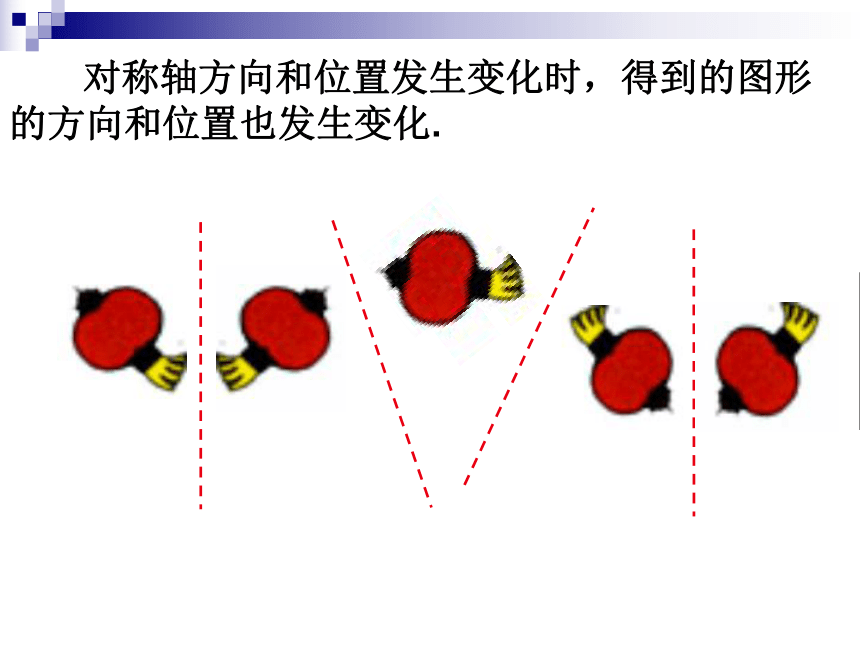
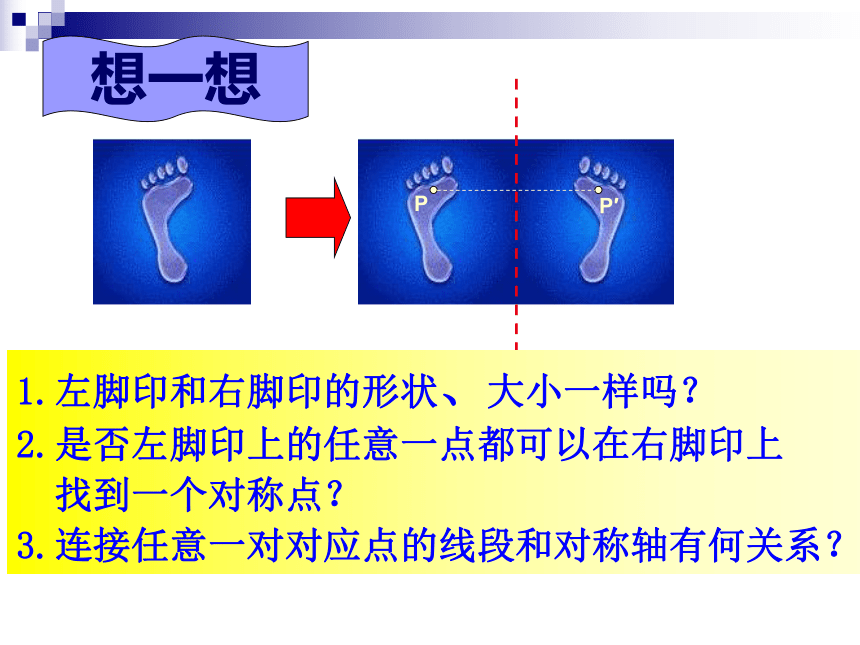
利用轴对称进行简单的图案设计.2.能作出已知图形关于某条直线对称的图形.利用轴对称变换设计美丽图案 在一张半透明的纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.这时,右脚印和左脚印成轴对称。 类似地,我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案. 对称轴方向和位置发生变化时,得到的图形的方向和位置也发生变化.想一想1.左脚印和右脚印的形状、大小一样吗?
2.是否左脚印上的任意一点都可以在右脚印上
找到一个对称点?
3.连接任意一对对应点的线段和对称轴有何关系?PP′1.由一个平面图形可以得到它关于一条直线L对称
的图形,这个图形与原图形的( )
完全相同;2.新图形上的每一点,都是原图形上的某一点关于
直线 l 的( ); 3.连接任意一对对应点的线段被对称轴( ). 答一答形状和大小对称点垂直平分轴对称变换的特征是什么?想一想 如果有一个图形和一条直线,如何作出这个图形关于这条直线
对称的图形呢?A′AO l 试一试作法:
过点A作直线l的垂线垂足为点O,在垂线上截取OA′=OA.
∴点A′就是点A关于直线 l 的对称点.
已知直线 l 和一个点A,如何画出点A关于 直线l 的对称点A′ ?试一试作法:
1.过点A作直线 l 的垂线,
垂足为点O,在垂线上截取 OA′=OA,点A′就是点A
关于直线 l 的对称点;
2.类似地,作出点B关于直
线 l 的对称点B′;
3.连接A′B′.
l 如何画线段AB关于直线 l 的对称线段 ?∴ 线段A′B′即为所求。1.过点A作直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l 的对称点; 如图,已知△ABC和直线l,作出与△ABC关于直线l 对称的图形。l作法:2.类似地,分别作出点B、C关于直线l 的对称点B′、C′;A′B′C′O例1C′C′ 如图,已知△ABC和直线l,作出与△ABC关于直线l 对称的图形.变式1A′B′A′B′C′B′A′ 如图,已知四边形ABCD和直线l,作出与四边形ABCD关于直线l 对称的图形.变式2A′B′C′D′ 如图,已知五边形ABCDE和直线l,作出与五边形ABCDE关于直线l 对称的图形.变式3B′C′D′A′E′1.找点2.画点3.连线(确定图形中的一些特殊点);(画出特殊点关于已知直线的对称点);(连接对称点)。作已知图形关于已知直线对称的图形的一般步聚:我来总结练一练如图,把下列图形补成关于直线 l 对称的图形.利用轴对称,可以设计出精美的图案。请欣赏下列美丽的图案,体会轴对称在现实生活中的应用。中外建筑《委加·派尔》
1969法国著名画家 V·瓦萨雷利学习体会学习目标:对照学习目标,说说你的收获.1.通过探索简单图形之间的轴对称关系,理解轴对称变
换的特征;2.能作出已知图形关于某条直线对称的图形; 3.认识和欣赏轴对称在现实生活中的应用,能利用轴对
称进行简单的图案设计.(①找点 ②画点 ③连线)基础与达标参考答案1.作业:1.必做作业:
书面作业:课本P45 习题第1题;
动手实践:课本P41 练习第2题.2.选做作业:
书面作业:课本P46 习题第10题;
动手实践:课本P47 习题第10题.3.完成下节预习.
解轴对称变换的特征.3.认识和欣赏轴对称在现实生活中的应用,能
利用轴对称进行简单的图案设计.2.能作出已知图形关于某条直线对称的图形.利用轴对称变换设计美丽图案 在一张半透明的纸的左边部分,画一只左脚印,把这张纸对折后描图,打开对折的纸,就能得到相应的右脚印.这时,右脚印和左脚印成轴对称。 类似地,我们可由一个图形得到与它成轴对称的另一个图形,重复此过程,可得到美丽的图案. 对称轴方向和位置发生变化时,得到的图形的方向和位置也发生变化.想一想1.左脚印和右脚印的形状、大小一样吗?
2.是否左脚印上的任意一点都可以在右脚印上
找到一个对称点?
3.连接任意一对对应点的线段和对称轴有何关系?PP′1.由一个平面图形可以得到它关于一条直线L对称
的图形,这个图形与原图形的( )
完全相同;2.新图形上的每一点,都是原图形上的某一点关于
直线 l 的( ); 3.连接任意一对对应点的线段被对称轴( ). 答一答形状和大小对称点垂直平分轴对称变换的特征是什么?想一想 如果有一个图形和一条直线,如何作出这个图形关于这条直线
对称的图形呢?A′AO l 试一试作法:
过点A作直线l的垂线垂足为点O,在垂线上截取OA′=OA.
∴点A′就是点A关于直线 l 的对称点.
已知直线 l 和一个点A,如何画出点A关于 直线l 的对称点A′ ?试一试作法:
1.过点A作直线 l 的垂线,
垂足为点O,在垂线上截取 OA′=OA,点A′就是点A
关于直线 l 的对称点;
2.类似地,作出点B关于直
线 l 的对称点B′;
3.连接A′B′.
l 如何画线段AB关于直线 l 的对称线段 ?∴ 线段A′B′即为所求。1.过点A作直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l 的对称点; 如图,已知△ABC和直线l,作出与△ABC关于直线l 对称的图形。l作法:2.类似地,分别作出点B、C关于直线l 的对称点B′、C′;A′B′C′O例1C′C′ 如图,已知△ABC和直线l,作出与△ABC关于直线l 对称的图形.变式1A′B′A′B′C′B′A′ 如图,已知四边形ABCD和直线l,作出与四边形ABCD关于直线l 对称的图形.变式2A′B′C′D′ 如图,已知五边形ABCDE和直线l,作出与五边形ABCDE关于直线l 对称的图形.变式3B′C′D′A′E′1.找点2.画点3.连线(确定图形中的一些特殊点);(画出特殊点关于已知直线的对称点);(连接对称点)。作已知图形关于已知直线对称的图形的一般步聚:我来总结练一练如图,把下列图形补成关于直线 l 对称的图形.利用轴对称,可以设计出精美的图案。请欣赏下列美丽的图案,体会轴对称在现实生活中的应用。中外建筑《委加·派尔》
1969法国著名画家 V·瓦萨雷利学习体会学习目标:对照学习目标,说说你的收获.1.通过探索简单图形之间的轴对称关系,理解轴对称变
换的特征;2.能作出已知图形关于某条直线对称的图形; 3.认识和欣赏轴对称在现实生活中的应用,能利用轴对
称进行简单的图案设计.(①找点 ②画点 ③连线)基础与达标参考答案1.作业:1.必做作业:
书面作业:课本P45 习题第1题;
动手实践:课本P41 练习第2题.2.选做作业:
书面作业:课本P46 习题第10题;
动手实践:课本P47 习题第10题.3.完成下节预习.
