2021-2022学年高一上学期数学人教A版(2019)必修第一册3.4函数的应用—停车距离问题说课课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册3.4函数的应用—停车距离问题说课课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 17:39:29 | ||
图片预览








文档简介
(共23张PPT)
停车距离问题
普通高中课程标准(2017版)
教学内容分析
教学目标设置
教学策略分析
说课内容
教学过程分析
学生学情分析
平面与平面垂直——复习课
教学内容分析
目标分析
学情分析
教学策略
本节课《停车距离问题》就是身边熟悉的实际问题,通过让学生思考汽车制动过程,分析出影响停车距离的主要因素,初步建立停车距离模型:停车距离=反应距离+制动距离。师生共同亲历数学建模的完整过程。这个过程进一步突出了数学源于生活,用于生活的思想。让学生成为主体多参与,多思考,激发学生的学习热情,初步了解建模的步骤,提升数学建模和数学运算的核心素养。
教学过程
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法建构模型解决问题的素养。数学建模过程主要包括在实际情景中,从数学的视角发现问题、提出问题,分析问题、建构模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题。数学建模活动是基于数学思维,运用模型解决实际问题的一类综合实践活动,是高中阶段数学课程的重要内容。
平面与平面垂直——复习课
教学内容分析
目标分析
学情分析
教学策略
教学过程
教学
重点
数学模型的建立过程
学分析
02
01
03
初步掌握数学建模的步骤,能运用数学知识解决停车距离问题。
通过学习学生能有意识地用数学语言表达现实世界,发现和提出问题,感悟数学与现实间的联系。
目标分析
学情分析
教学策略
教学过程
学会用数学模型解决实际问题,积累数学实践的经验,提升实践能力,增强创新意识和科学精神。
教学目标设置
内容分析
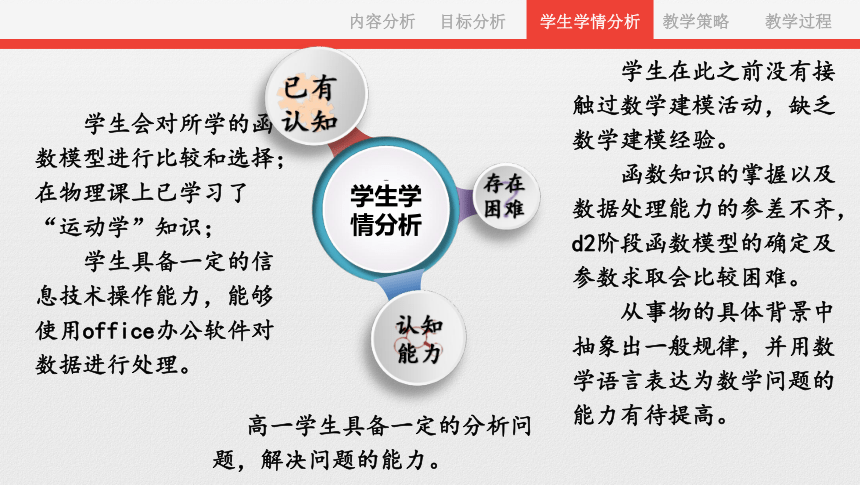
学生会对所学的函数模型进行比较和选择;
在物理课上已学习了
“运动学”知识;
学生具备一定的信息技术操作能力,能够使用office办公软件对数据进行处理。
内容分析
目标分析
学生学情分析
教学策略
教学过程
点击添加
学生学情分析
学生在此之前没有接触过数学建模活动,缺乏数学建模经验。
函数知识的掌握以及数据处理能力的参差不齐,d2阶段函数模型的确定及参数求取会比较困难。
从事物的具体背景中抽象出一般规律,并用数学语言表达为数学问题的能力有待提高。
高一学生具备一定的分析问题,解决问题的能力。
存在困难
已有认知
认知能力
平面与平面垂直——复习课
目标分析
学情分析
教学策略
教学过程
教学
难点
对函数模型的合理选择以及对参数的计算。
学生学情分析
内容分析
平面与平面垂直——复习课
教学策略分析
内容分析
学情分析
目标分析
教学过程
01
OPTION
02
OPTION
03
OPTION
自主探究、合作学习:让学生自主经历解决实际问题的过程当中。
适时引导、规范实施:
注意了解学生活动开展情况,观察学生的表现,给予帮助引导,规范撰写研究报告。
多样化评价、交流方式:让学生进行反思性自我评价与交流,思维碰撞是使学生学会建立数学模型,解决问题的重要手段。
教学策略分析
平面与平面垂直——复习课
教学过程分析
环节一——选题活动
[情境] 观看交通追尾事故视频
[教师过渡]道路安全法规定“当汽车行驶速度超过100公里/小时,与同车道前车距离要保持100米以上”,为什么要确定100米以上的车距呢?
一、创设情境 导入新课
平面与平面垂直——复习课
教学过程分析
二、提出假设 建立模型
[问题1] 影响汽车停车距离的因素有哪些?
[预设]
生1:汽车的车速。
生2:汽车的重量。
生3:轮胎。
生4:制动系统。
生5:天气情况,路况。
生6:驾驶员反应。
[问题2] 如果对安全驾驶提供建议,你觉得主要因素是什么呢?
平面与平面垂直——复习课
教学过程分析
师生共同讨论得到:可控因素主要是车速,故可对模型作如下假设:
1)假设车辆类型轮胎类型相同;
2)假设汽车制动器的性能正常,道路、气候视为不变;
3)假设汽车没有超载;
4)假设刹车系统的机械状况、驾驶员状况良好;
5)假设汽车在平直道路上行驶。
平面与平面垂直——复习课
教学过程分析
[活动1] 你能描述在行车中,从发现障碍物到车辆停止,驾驶员及车辆经历的过程吗?
[预设] 驾驶员眼睛看到障碍物后有一段反应时间,然后再脚踩刹车。从看到障碍物到脚踩刹车,车辆已经行驶了一段距离,从脚踩刹车到车辆停下来,车辆又行驶了一段距离。
平面与平面垂直——复习课
教学过程分析
[问题3] 你能用生活语言表述停车距离的模型吗?
析出模型:停车距离=反应距离+制动距离
设计意图:从学生身边熟悉的问题导入,引导学生从事物的具体背景中抽象出一般规律,并用数学语言表达为数学问题,这是一个用数学的眼光观察世界,并发现问题和提出问题的过程,为建立模型做准备。
平面与平面垂直——复习课
教学过程分析
环节二——开题活动
[活动1] 各课题小组代表介绍开题报告
平面与平面垂直——复习课
教学过程分析
[预设]
生:1.建立模型:利用物理知识来分析,第一阶段是匀速直线运动,d1=vt是正比例函数。第二阶段是匀速直线运动,d2与v是二次函数关系。停车距离d=d1+d2,得d=αv+βv2。
2.确定参数,计算求解。收集数据,网络查找数据资料。通过函数关系d1=αv和d2=βv2可以计算出相应的α和β的值,它们的平均数可以作为参数的估计值。
3.模型检验。代入车速v,利用真实实践数据与函数求解数据进行比较。分析误差,对模型进行优化。
生:网络查找数据资料,借助画散点图来呈现数据,这样比较直观。利用excel线性拟合,根据图像的变化趋势得到d1是正比例函数,d2是二次函数关系,确定函数模型d=αv+βv2。
平面与平面垂直——复习课
教学过程分析
生:网络查找数据资料,借助画散点图来呈现数据,利用excel线性拟合,根据图像的变化趋势得到d是二次函数模型,确定函数模型d=αv+βv2。
生:利用物理知识确定d1阶段为正比例函数模型;网络查找数据资料,借助画散点图来呈现数据,利用excel线性拟合,根据图像的变化趋势得到d2是二次函数模型,确定函数模型d=αv+βv2。
生:网络查找数据资料,求取d1,d2,v的平均数,通过函数关系d1=αv和d2=βv2可以计算出相应的α和β的值。
生:利用小车模拟实验收集数据。
平面与平面垂直——复习课
教学过程分析
[活动2] 请同学们集思广益,对各小组开题报告交流评价
教师组织学生对开题报告进行评价,可以从设计的周密性、实施的方便性、是否便于操作、存在哪些缺陷或不足等方面展开。
设计意图:让学生初步形成解决问题大致思路和方案。教师组织学生采用多样化的交流,用“头脑风暴”的形式集思广益,并给出评价。鼓励学生大胆陈述,表达自己的想法和建议,培养学生数学语言表达能力。做到真正把课堂交给学生,以学生为主体开展教学活动。
平面与平面垂直——复习课
教学过程分析
环节三——做题活动
[活动] 对开题方案改进并操作实施
[预设] 教师了解学生活动进展情况,观察学生的表现,帮助有困难的小组解决问题。
设计意图:让学生自主合作解决问题,在此过程中进一步培养学生数据分析,直观想象,逻辑推理,数学运算等学科素养。
平面与平面垂直——复习课
教学过程分析
环节四——结题活动
[活动1] 各课题小组代表结题汇报
[预设] 教师对获得的结果可以从数据的可靠性、推导过程的严谨性、模型的适用范围等进行评价。还要让学生对参与建模活动的过程和收获作出评价。例如,小组分工合作,发挥成员的特长,遇到哪些困难或问题,如何克服困难和解决问题,数学知识再解决问题中有怎样的作用,对有关数学知识的新理解,有哪些能力得到提升。
[活动2] 结合以上探究过程,你能尝试归纳数学模型建立的一般步骤吗?
平面与平面垂直——复习课
教学过程分析
[活动2] 结合以上探究过程,你能尝试归纳数学模型建立的一般步骤吗?
收集数据
发现和提出问题
选择函数模型
观察实际情景
求解函数模型
应用函数模型解决实际问题
检验模型
符合
不符合实际
平面与平面垂直——复习课
教学过程分析
[活动3] 谈谈经历了数学建模的过程你有什么收获?
设计意图:让学生完整经历建立模型、确定参数、计算求解、检验结果、改进模型、最终解决实际问题的过程,使学生能经历完整系统的从知识到应用的学习过程,这样才能满足学生数学思维发展的需求,在建模中体会到数学建模的核心。进一步提高学生的实践能力和数学应用能力
平面与平面垂直——复习课
教学反思
1.在这之前数学建模内容教学重视程度不够,对于教师、学生都缺乏数学建模经验。加之时间较紧,条件不足,没能达到预期效果。另外,教师扑捉学生问题并能及时准确给出评价的素养不够,使得开题阶段学生很多问题没有得到很好解决,仅流于形式,为后面各环节的处理埋下隐患。
2.最终结题报告中为了便于查阅,给驾驶员安全提供更好建议,应当给出一个更加直观清晰的急刹车的停车距离模型。
3.结题中仅对模型进行了检验,分析了误差原因,但出现误差并没有强调学生做到进一步对模型进行合理再优化。
4.最后一位结题报告同学模型中是带常数项的数学模型,与现实实际情况不符,没能及时给出评价。这说明教师对这一问题的最初认识也存在不到位现象。
这次教学我本人在以往常态教学中没有的,是一次尝试,是一次学习,是一次反思,是一次进步。“数学已经从幕后走到台前,直接为社会创造价值”高中数学必须重视数学应用,加强数学建模活动的课程。作为高中数学教师,我应当跟紧高中数学教学理念,落实学生学科核心素养,进一步提高学生实践能力和数学应用能力。
谢
谢
停车距离问题
普通高中课程标准(2017版)
教学内容分析
教学目标设置
教学策略分析
说课内容
教学过程分析
学生学情分析
平面与平面垂直——复习课
教学内容分析
目标分析
学情分析
教学策略
本节课《停车距离问题》就是身边熟悉的实际问题,通过让学生思考汽车制动过程,分析出影响停车距离的主要因素,初步建立停车距离模型:停车距离=反应距离+制动距离。师生共同亲历数学建模的完整过程。这个过程进一步突出了数学源于生活,用于生活的思想。让学生成为主体多参与,多思考,激发学生的学习热情,初步了解建模的步骤,提升数学建模和数学运算的核心素养。
教学过程
数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法建构模型解决问题的素养。数学建模过程主要包括在实际情景中,从数学的视角发现问题、提出问题,分析问题、建构模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题。数学建模活动是基于数学思维,运用模型解决实际问题的一类综合实践活动,是高中阶段数学课程的重要内容。
平面与平面垂直——复习课
教学内容分析
目标分析
学情分析
教学策略
教学过程
教学
重点
数学模型的建立过程
学分析
02
01
03
初步掌握数学建模的步骤,能运用数学知识解决停车距离问题。
通过学习学生能有意识地用数学语言表达现实世界,发现和提出问题,感悟数学与现实间的联系。
目标分析
学情分析
教学策略
教学过程
学会用数学模型解决实际问题,积累数学实践的经验,提升实践能力,增强创新意识和科学精神。
教学目标设置
内容分析
学生会对所学的函数模型进行比较和选择;
在物理课上已学习了
“运动学”知识;
学生具备一定的信息技术操作能力,能够使用office办公软件对数据进行处理。
内容分析
目标分析
学生学情分析
教学策略
教学过程
点击添加
学生学情分析
学生在此之前没有接触过数学建模活动,缺乏数学建模经验。
函数知识的掌握以及数据处理能力的参差不齐,d2阶段函数模型的确定及参数求取会比较困难。
从事物的具体背景中抽象出一般规律,并用数学语言表达为数学问题的能力有待提高。
高一学生具备一定的分析问题,解决问题的能力。
存在困难
已有认知
认知能力
平面与平面垂直——复习课
目标分析
学情分析
教学策略
教学过程
教学
难点
对函数模型的合理选择以及对参数的计算。
学生学情分析
内容分析
平面与平面垂直——复习课
教学策略分析
内容分析
学情分析
目标分析
教学过程
01
OPTION
02
OPTION
03
OPTION
自主探究、合作学习:让学生自主经历解决实际问题的过程当中。
适时引导、规范实施:
注意了解学生活动开展情况,观察学生的表现,给予帮助引导,规范撰写研究报告。
多样化评价、交流方式:让学生进行反思性自我评价与交流,思维碰撞是使学生学会建立数学模型,解决问题的重要手段。
教学策略分析
平面与平面垂直——复习课
教学过程分析
环节一——选题活动
[情境] 观看交通追尾事故视频
[教师过渡]道路安全法规定“当汽车行驶速度超过100公里/小时,与同车道前车距离要保持100米以上”,为什么要确定100米以上的车距呢?
一、创设情境 导入新课
平面与平面垂直——复习课
教学过程分析
二、提出假设 建立模型
[问题1] 影响汽车停车距离的因素有哪些?
[预设]
生1:汽车的车速。
生2:汽车的重量。
生3:轮胎。
生4:制动系统。
生5:天气情况,路况。
生6:驾驶员反应。
[问题2] 如果对安全驾驶提供建议,你觉得主要因素是什么呢?
平面与平面垂直——复习课
教学过程分析
师生共同讨论得到:可控因素主要是车速,故可对模型作如下假设:
1)假设车辆类型轮胎类型相同;
2)假设汽车制动器的性能正常,道路、气候视为不变;
3)假设汽车没有超载;
4)假设刹车系统的机械状况、驾驶员状况良好;
5)假设汽车在平直道路上行驶。
平面与平面垂直——复习课
教学过程分析
[活动1] 你能描述在行车中,从发现障碍物到车辆停止,驾驶员及车辆经历的过程吗?
[预设] 驾驶员眼睛看到障碍物后有一段反应时间,然后再脚踩刹车。从看到障碍物到脚踩刹车,车辆已经行驶了一段距离,从脚踩刹车到车辆停下来,车辆又行驶了一段距离。
平面与平面垂直——复习课
教学过程分析
[问题3] 你能用生活语言表述停车距离的模型吗?
析出模型:停车距离=反应距离+制动距离
设计意图:从学生身边熟悉的问题导入,引导学生从事物的具体背景中抽象出一般规律,并用数学语言表达为数学问题,这是一个用数学的眼光观察世界,并发现问题和提出问题的过程,为建立模型做准备。
平面与平面垂直——复习课
教学过程分析
环节二——开题活动
[活动1] 各课题小组代表介绍开题报告
平面与平面垂直——复习课
教学过程分析
[预设]
生:1.建立模型:利用物理知识来分析,第一阶段是匀速直线运动,d1=vt是正比例函数。第二阶段是匀速直线运动,d2与v是二次函数关系。停车距离d=d1+d2,得d=αv+βv2。
2.确定参数,计算求解。收集数据,网络查找数据资料。通过函数关系d1=αv和d2=βv2可以计算出相应的α和β的值,它们的平均数可以作为参数的估计值。
3.模型检验。代入车速v,利用真实实践数据与函数求解数据进行比较。分析误差,对模型进行优化。
生:网络查找数据资料,借助画散点图来呈现数据,这样比较直观。利用excel线性拟合,根据图像的变化趋势得到d1是正比例函数,d2是二次函数关系,确定函数模型d=αv+βv2。
平面与平面垂直——复习课
教学过程分析
生:网络查找数据资料,借助画散点图来呈现数据,利用excel线性拟合,根据图像的变化趋势得到d是二次函数模型,确定函数模型d=αv+βv2。
生:利用物理知识确定d1阶段为正比例函数模型;网络查找数据资料,借助画散点图来呈现数据,利用excel线性拟合,根据图像的变化趋势得到d2是二次函数模型,确定函数模型d=αv+βv2。
生:网络查找数据资料,求取d1,d2,v的平均数,通过函数关系d1=αv和d2=βv2可以计算出相应的α和β的值。
生:利用小车模拟实验收集数据。
平面与平面垂直——复习课
教学过程分析
[活动2] 请同学们集思广益,对各小组开题报告交流评价
教师组织学生对开题报告进行评价,可以从设计的周密性、实施的方便性、是否便于操作、存在哪些缺陷或不足等方面展开。
设计意图:让学生初步形成解决问题大致思路和方案。教师组织学生采用多样化的交流,用“头脑风暴”的形式集思广益,并给出评价。鼓励学生大胆陈述,表达自己的想法和建议,培养学生数学语言表达能力。做到真正把课堂交给学生,以学生为主体开展教学活动。
平面与平面垂直——复习课
教学过程分析
环节三——做题活动
[活动] 对开题方案改进并操作实施
[预设] 教师了解学生活动进展情况,观察学生的表现,帮助有困难的小组解决问题。
设计意图:让学生自主合作解决问题,在此过程中进一步培养学生数据分析,直观想象,逻辑推理,数学运算等学科素养。
平面与平面垂直——复习课
教学过程分析
环节四——结题活动
[活动1] 各课题小组代表结题汇报
[预设] 教师对获得的结果可以从数据的可靠性、推导过程的严谨性、模型的适用范围等进行评价。还要让学生对参与建模活动的过程和收获作出评价。例如,小组分工合作,发挥成员的特长,遇到哪些困难或问题,如何克服困难和解决问题,数学知识再解决问题中有怎样的作用,对有关数学知识的新理解,有哪些能力得到提升。
[活动2] 结合以上探究过程,你能尝试归纳数学模型建立的一般步骤吗?
平面与平面垂直——复习课
教学过程分析
[活动2] 结合以上探究过程,你能尝试归纳数学模型建立的一般步骤吗?
收集数据
发现和提出问题
选择函数模型
观察实际情景
求解函数模型
应用函数模型解决实际问题
检验模型
符合
不符合实际
平面与平面垂直——复习课
教学过程分析
[活动3] 谈谈经历了数学建模的过程你有什么收获?
设计意图:让学生完整经历建立模型、确定参数、计算求解、检验结果、改进模型、最终解决实际问题的过程,使学生能经历完整系统的从知识到应用的学习过程,这样才能满足学生数学思维发展的需求,在建模中体会到数学建模的核心。进一步提高学生的实践能力和数学应用能力
平面与平面垂直——复习课
教学反思
1.在这之前数学建模内容教学重视程度不够,对于教师、学生都缺乏数学建模经验。加之时间较紧,条件不足,没能达到预期效果。另外,教师扑捉学生问题并能及时准确给出评价的素养不够,使得开题阶段学生很多问题没有得到很好解决,仅流于形式,为后面各环节的处理埋下隐患。
2.最终结题报告中为了便于查阅,给驾驶员安全提供更好建议,应当给出一个更加直观清晰的急刹车的停车距离模型。
3.结题中仅对模型进行了检验,分析了误差原因,但出现误差并没有强调学生做到进一步对模型进行合理再优化。
4.最后一位结题报告同学模型中是带常数项的数学模型,与现实实际情况不符,没能及时给出评价。这说明教师对这一问题的最初认识也存在不到位现象。
这次教学我本人在以往常态教学中没有的,是一次尝试,是一次学习,是一次反思,是一次进步。“数学已经从幕后走到台前,直接为社会创造价值”高中数学必须重视数学应用,加强数学建模活动的课程。作为高中数学教师,我应当跟紧高中数学教学理念,落实学生学科核心素养,进一步提高学生实践能力和数学应用能力。
谢
谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
