20.1数据的频数分布课件2021—2022学年沪科版数学八年级下册(共19张ppt)
文档属性
| 名称 | 20.1数据的频数分布课件2021—2022学年沪科版数学八年级下册(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 15:04:09 | ||
图片预览






文档简介
(共19张PPT)
20.1 数据的频数分布
知识回顾
我们已经学习了用哪些方法来
描述数据?
统计表;条形图;折线图;
扇形图.
各方法有什么特点?
条形统计图可以清楚地表示出每个项目的具体数目
折线统计图可以清楚地反映事物变化的情况
扇形统计图可以清楚地表示各部分在总体中所占的百分比
复习
你还记得各个统计图的特点:
沙尘暴袭我国北方2.7亿人受苦 或蔓延至长江以南
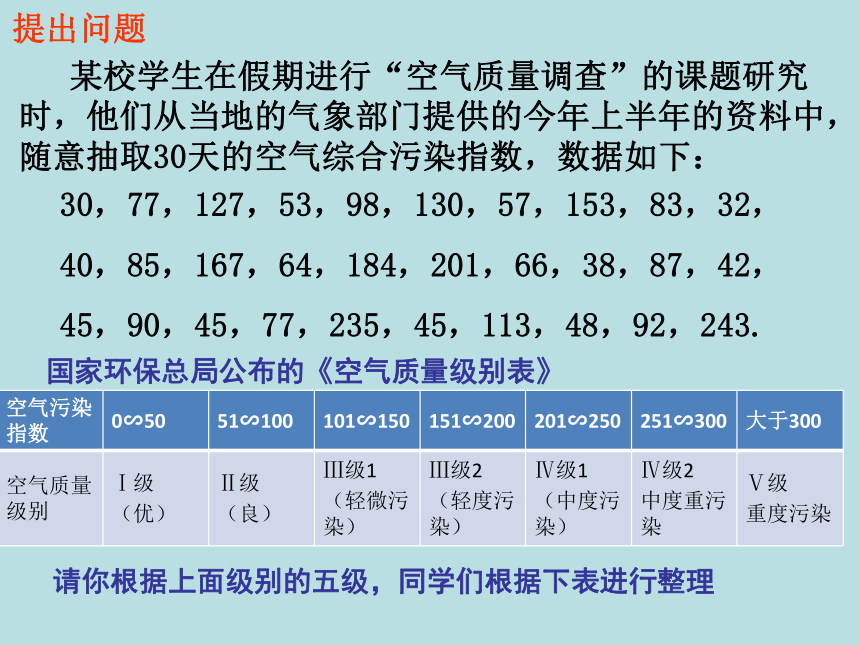
某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
提出问题
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0∽50 51∽100 101∽150 151∽200 201∽250 251∽300 大于300
空气质量级别 Ⅰ级
(优) Ⅱ级
(良) Ⅲ级1
(轻微污染) Ⅲ级2
(轻度污染) Ⅳ级1
(中度污染) Ⅳ级2
中度重污染 Ⅴ级
重度污染
请你根据上面级别的五级,同学们根据下表进行整理
(1)说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
(2)该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
空气污染指数 0∽50 51∽100 101∽150 151∽200 201∽250 251∽300 大于300
天数
9
12
3
3
3
0
0
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
问题1启示我们:
面对大量的数据,要想从中获取所需要的信息。
(1)、常常先要选择好合适的统计表,把相差不大的数据放在一起,进行适当的分组,
(2)然后统计出落在各个小组内数据的个数,并借助表格将分组结果及各组数据的个数进行整理,
这样,便能反映出这批数据的分布规律。
下面我们就来通过具体的例子,学习这种分析数据的分布方法
40,21,35,24,40,38,23,52,35,62,
36,15,51,45,42,40,32,43,36,34,
53,38,40,39,32,45,40,50,45,40,
50,26,45,40,45,35,40,42,45,40。
为了了解这批数据反映的情况,可以对它们进行怎样的分析呢?
问题2
某校体卫组对该校八年级学生一周内平均每天参加课外体育锻炼的时间(单位:min)有所了解,从中随机抽查了40名学生,结果如下:
例: 某中学九年级部分同学参加全国初中数学竞赛,指
导老师统计了所有参赛同学的成绩(成绩都是整数,试
题满分120分),并且绘制了频数分布直方图,如图所
示,请根据直方图回答下列问题:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那
么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满
分的同学等等。请再写出两条信息。
60
70
80
90
100
110
120
分数(分)
人数(人)
(每组含最低分,不含最高分)
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛
的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛
同学获奖率是43.75 %;
(3)该中学参赛同学的成绩均不低于60分;成绩在
80~90分数段的人数最多。
60
70
80
90
100
110
120
分数(分)
人数(人)
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等。请再写出两条信息。
例题:我校八年级(1)班共有学生50名,该班学生的身高(单位:cm)的频数分布如下:
根据所给表格回答:
(1)身高在161.5以上的学生有多少?占全班人数的百分之几?
分组 136.5∽141.5 141.5∽146.5 146.5∽151.5 151.5∽156.5 156.5∽161.5 161.5∽166.6 166.5∽171.5 171.5∽176.5 合计
频数 1 4 10 15 9 8 2 1 50
(2)估计我校八年级400名学生中身高在161.5以上的约有多少人?
解:身高在161.5以上的学生有:8+2+1=11
占全班人数的百分比是:
八年级学生身高在161.5以上的学生有:
答:
报纸42期
①对某班40名学生数学成绩进行统计,80~90分小组的频率是20%,则成绩在80~90这个分数段的人数是_____人
②一组数据的最大值是125,最小值是34,若确定组距是14,则组数是_____
③将50个数据分成3组,第一组频率是0.2,第三组频率是0.5,则第二组频率是____
④小红1分钟内共投篮20次,投进8个球,则小红投进球的概率是_____
下表是随机抽取的部分同学的视力情况频数分布表
视力 频数 频率
3.95~4.25 2 0.04
9 0.18
4.55~4.85 20
4.85~5.15
5.15~5.45 1 0.02
合计 1.00
4.25~4.55
0.40
18
0.36
50
请把上表补充完整;
如果视力在4.85以下就属于不正常范围,那么请你分析一下我们学校的视力情况,看到这种情况,你想对周围的同学说些什么?
3.95
视力
人数
22
20
16
14
12
10
8
6
4
2
18
4.25
4.55
4.85
5.15
5.45
报纸42期版4:
“细说频数与频率”
例3
课本P112 T2
课本P113 T4如图是某班全体学生年龄的频数分布直方图.根据图中提供的信息,画出该班学生年龄分布扇形统计图。
报纸42期版4:
“统计图表为你打开信息之门”例1
课后 小结:
梨25%
桃12.5%
通过本课的探索,你学到了什么?有何收获?
1. 学会使用统计表、统计图使数据一目了然。
2. 注意:
(1)组距要相等,组数要合适。
(2)分点数据要多位。
(3)频数、频率要分清。
3.通过解读收集并处理有价值的信息,以便我们能作出科学合理地决策。数据一般总是中间多,两头少呈正态分布。
20.1 数据的频数分布
知识回顾
我们已经学习了用哪些方法来
描述数据?
统计表;条形图;折线图;
扇形图.
各方法有什么特点?
条形统计图可以清楚地表示出每个项目的具体数目
折线统计图可以清楚地反映事物变化的情况
扇形统计图可以清楚地表示各部分在总体中所占的百分比
复习
你还记得各个统计图的特点:
沙尘暴袭我国北方2.7亿人受苦 或蔓延至长江以南
某校学生在假期进行“空气质量调查”的课题研究时,他们从当地的气象部门提供的今年上半年的资料中,随意抽取30天的空气综合污染指数,数据如下:
国家环保总局公布的《空气质量级别表》
提出问题
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
空气污染指数 0∽50 51∽100 101∽150 151∽200 201∽250 251∽300 大于300
空气质量级别 Ⅰ级
(优) Ⅱ级
(良) Ⅲ级1
(轻微污染) Ⅲ级2
(轻度污染) Ⅳ级1
(中度污染) Ⅳ级2
中度重污染 Ⅴ级
重度污染
请你根据上面级别的五级,同学们根据下表进行整理
(1)说说这30天的空气质量,根据国家公布的级别,各级别各占多大比率(即分布情况)
(2)该校学生估计该地今年(按365天计算)空气质量达到优级别的天数约是110天,你知道他们是怎样估计出这个结论的?
空气污染指数 0∽50 51∽100 101∽150 151∽200 201∽250 251∽300 大于300
天数
9
12
3
3
3
0
0
30,77,127,53,98,130,57,153,83,32,
40,85,167,64,184,201,66,38,87,42,
45,90,45,77,235,45,113,48,92,243.
问题1启示我们:
面对大量的数据,要想从中获取所需要的信息。
(1)、常常先要选择好合适的统计表,把相差不大的数据放在一起,进行适当的分组,
(2)然后统计出落在各个小组内数据的个数,并借助表格将分组结果及各组数据的个数进行整理,
这样,便能反映出这批数据的分布规律。
下面我们就来通过具体的例子,学习这种分析数据的分布方法
40,21,35,24,40,38,23,52,35,62,
36,15,51,45,42,40,32,43,36,34,
53,38,40,39,32,45,40,50,45,40,
50,26,45,40,45,35,40,42,45,40。
为了了解这批数据反映的情况,可以对它们进行怎样的分析呢?
问题2
某校体卫组对该校八年级学生一周内平均每天参加课外体育锻炼的时间(单位:min)有所了解,从中随机抽查了40名学生,结果如下:
例: 某中学九年级部分同学参加全国初中数学竞赛,指
导老师统计了所有参赛同学的成绩(成绩都是整数,试
题满分120分),并且绘制了频数分布直方图,如图所
示,请根据直方图回答下列问题:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那
么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满
分的同学等等。请再写出两条信息。
60
70
80
90
100
110
120
分数(分)
人数(人)
(每组含最低分,不含最高分)
解:(1)4+6+8+7+5+2=32,所以参加本次数学竞赛
的有32名同学;
(2)(7+5+2)÷32=43.75%,所以该中学的参赛
同学获奖率是43.75 %;
(3)该中学参赛同学的成绩均不低于60分;成绩在
80~90分数段的人数最多。
60
70
80
90
100
110
120
分数(分)
人数(人)
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)图中还提供了其他数据,例如该中学没有获得满分的同学等等。请再写出两条信息。
例题:我校八年级(1)班共有学生50名,该班学生的身高(单位:cm)的频数分布如下:
根据所给表格回答:
(1)身高在161.5以上的学生有多少?占全班人数的百分之几?
分组 136.5∽141.5 141.5∽146.5 146.5∽151.5 151.5∽156.5 156.5∽161.5 161.5∽166.6 166.5∽171.5 171.5∽176.5 合计
频数 1 4 10 15 9 8 2 1 50
(2)估计我校八年级400名学生中身高在161.5以上的约有多少人?
解:身高在161.5以上的学生有:8+2+1=11
占全班人数的百分比是:
八年级学生身高在161.5以上的学生有:
答:
报纸42期
①对某班40名学生数学成绩进行统计,80~90分小组的频率是20%,则成绩在80~90这个分数段的人数是_____人
②一组数据的最大值是125,最小值是34,若确定组距是14,则组数是_____
③将50个数据分成3组,第一组频率是0.2,第三组频率是0.5,则第二组频率是____
④小红1分钟内共投篮20次,投进8个球,则小红投进球的概率是_____
下表是随机抽取的部分同学的视力情况频数分布表
视力 频数 频率
3.95~4.25 2 0.04
9 0.18
4.55~4.85 20
4.85~5.15
5.15~5.45 1 0.02
合计 1.00
4.25~4.55
0.40
18
0.36
50
请把上表补充完整;
如果视力在4.85以下就属于不正常范围,那么请你分析一下我们学校的视力情况,看到这种情况,你想对周围的同学说些什么?
3.95
视力
人数
22
20
16
14
12
10
8
6
4
2
18
4.25
4.55
4.85
5.15
5.45
报纸42期版4:
“细说频数与频率”
例3
课本P112 T2
课本P113 T4如图是某班全体学生年龄的频数分布直方图.根据图中提供的信息,画出该班学生年龄分布扇形统计图。
报纸42期版4:
“统计图表为你打开信息之门”例1
课后 小结:
梨25%
桃12.5%
通过本课的探索,你学到了什么?有何收获?
1. 学会使用统计表、统计图使数据一目了然。
2. 注意:
(1)组距要相等,组数要合适。
(2)分点数据要多位。
(3)频数、频率要分清。
3.通过解读收集并处理有价值的信息,以便我们能作出科学合理地决策。数据一般总是中间多,两头少呈正态分布。
