华东师大版数学九年级上册 第24章解直角三角形复习题课件(共21张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 第24章解直角三角形复习题课件(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 20:18:26 | ||
图片预览








文档简介
(共21张PPT)
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA =
a
c
1、
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
*
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
特殊角三角函数值
1
角度逐渐增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
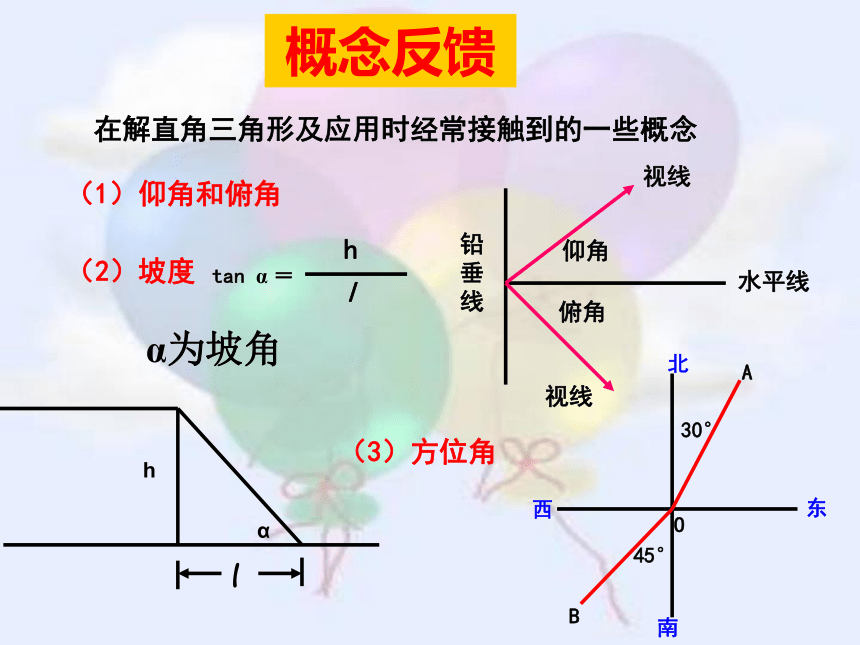
0在解直角三角形及应用时经常接触到的一些概念
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
·
例5一位同学测河宽,如图,在河岸上一点A观测河对岸边的一小树C,测得AC与河岸边的夹角为450,沿河岸边向前走200米到达B点,又观测河对岸边的小树C,测得BC与河岸边的夹角为300,问这位同学能否计算出河宽 若不能,请说明理由;若能,请你计算出河宽.
播放
停止
考点五:三角函数的实际应用
解 这位同学能计算出河宽.
在Rt△ACD中,设CD=x,由
∠ CAD=450,则CD=AD=x.
在Rt△BCD中,AB=200,
则BD=200+X,由∠CBD=300,
则tan300= 即
解得
所以河宽为
随堂演练
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图1,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
*
4.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图1),她测得CB=10米,∠ACB=50°,请你帮助她算出树高AB约为________米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
12
*
5.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米,已知小华的身高为1.6米,
那么分所住楼房的高度
为________米.
6.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为______米.
48
20
≈1.73)
7.如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发,
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
(参考数据:
≈1.41,
7.解:(1)设出发后x小时时两船与港口P的距离相等.
根据题意,得81-9x=18x,
解这个方程,得x=3.
∴出发后3小时两船与港口P的距离相等.
三边之间的关系
a2+b2=c2(勾股定理);
锐角之间的关系
∠ A+ ∠ B= 90
边角之间的关系(锐角三角函数)
tanA=
a
b
sinA =
a
c
1、
cosA=
b
c
A
C
B
a
b
c
解直角三角形的依据
*
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
特殊角三角函数值
1
角度逐渐增大
正弦值如何变化
正弦值也增大
余弦值如何变化
余弦值逐渐减小
正切值如何变化
正切值也随之增大
锐角A的正弦值、余弦值有无变化范围?
0< sinA<1
0
l
h
α
(2)坡度
tan α =
h
l
概念反馈
(1)仰角和俯角
视线
铅垂线
水平线
视线
仰角
俯角
(3)方位角
30°
45°
B
O
A
东
西
北
南
α为坡角
解直角三角形:(如图)
1.已知a,b.解直角三角形(即求:∠A,∠B及C边)
2. 已知∠A,a.解直角三角形
3.已知∠A,b. 解直角三角形
4. 已知∠A,c. 解直角三角形
b
A
B
C
a
┌
c
只有下面两种情况:
(1)已知两条边;
(2)已知一条边和一个锐角
·
例5一位同学测河宽,如图,在河岸上一点A观测河对岸边的一小树C,测得AC与河岸边的夹角为450,沿河岸边向前走200米到达B点,又观测河对岸边的小树C,测得BC与河岸边的夹角为300,问这位同学能否计算出河宽 若不能,请说明理由;若能,请你计算出河宽.
播放
停止
考点五:三角函数的实际应用
解 这位同学能计算出河宽.
在Rt△ACD中,设CD=x,由
∠ CAD=450,则CD=AD=x.
在Rt△BCD中,AB=200,
则BD=200+X,由∠CBD=300,
则tan300= 即
解得
所以河宽为
随堂演练
1. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为_______.
2. 在Rt△ABC中,∠C =90°,BC=4,AC=3,则cosA的值为______.
3. 如图1,在△ABC中,∠C =90°,BC=5,AC=12,则cosA等于( )
D
*
4.有人说,数学家就是不用爬树或把树砍倒就能够知道树高的人.小敏想知道校园内一棵大树的高(如图1),她测得CB=10米,∠ACB=50°,请你帮助她算出树高AB约为________米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
12
*
5.如图,小华为了测量所住楼房的高度,他请来同学帮忙,测量了同一时刻他自己的影长和楼房的影长分别是0.5米和15米,已知小华的身高为1.6米,
那么分所住楼房的高度
为________米.
6.如图,两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为______米.
48
20
≈1.73)
7.如图,小岛A在港口P的南偏西45°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东60°方向,以18海里/时的速度驶离港口,现两船同时出发,
(1)出发后几小时两船与港口P的距离相等?
(2)出发后几小时乙船在甲船的正东方向?(结果精确到0.1小时)
(参考数据:
≈1.41,
7.解:(1)设出发后x小时时两船与港口P的距离相等.
根据题意,得81-9x=18x,
解这个方程,得x=3.
∴出发后3小时两船与港口P的距离相等.
