2021-2022学年人教版八年级数学上册14.2乘法公式 期末综合复习知识点分类训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2乘法公式 期末综合复习知识点分类训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 194.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 19:20:57 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《14-2乘法公式》期末综合复习
知识点分类训练(附答案)
一.完全平方公式
1.下列运算正确的是( )
A.(a﹣b)2=a2﹣b2 B.2a+b=2ab
C.(a3)2=a6 D.(﹣2a)2=﹣4a4
2.下列运算正确的是( )
A.(1+2a)2=1+2a+4a2 B.a2+a3=a5
C.(2a3)3=6a9 D.a3 (﹣a)5=﹣a8
3.若x+y=6,x2+y2=20,求x﹣y的值是( )
A.2 B.﹣2 C.4 D.±2
4.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
5.若x2+y2=5,xy=2,则x﹣y= .
6.若x﹣y=3,xy=2,则x2+y2= .
7.已知(x﹣p)2=x2+mx+36,则m= .
8.小明将(2020x+2021)2展开后得到a1x2+b1x+c1;小红将(2021x﹣2020)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则c1﹣c2的值是 .
二.完全平方公式的几何背景
9.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形的面积来解释一些代数恒等式,例如图1可以用来解(a+b)2﹣(a﹣b)2=4ab,那么通过图2中阴影部分面积的计算验证的恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2
D.(a﹣b)(a+2b)=a2+ab﹣2b2
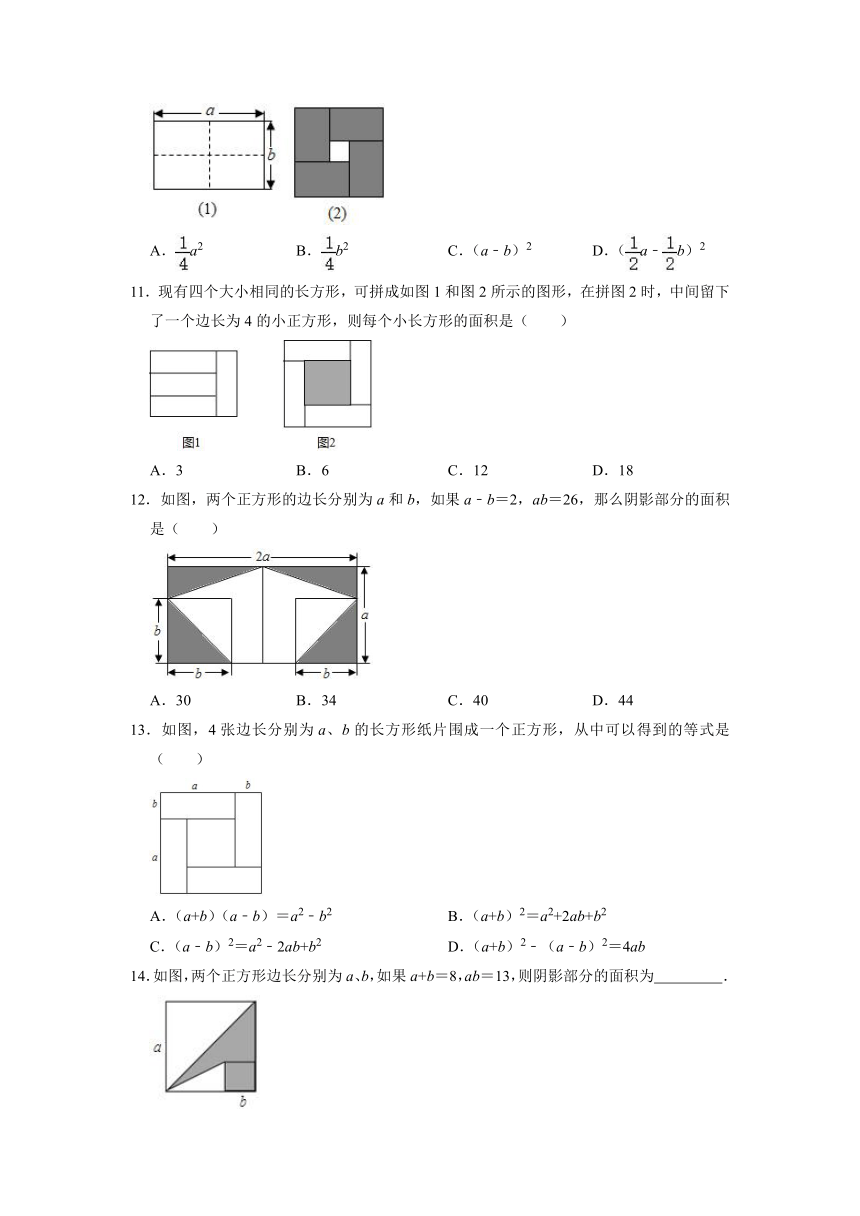
10.图(1)是一个长为a,宽为b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
A.a2 B.b2 C.(a﹣b)2 D.(a﹣b)2
11.现有四个大小相同的长方形,可拼成如图1和图2所示的图形,在拼图2时,中间留下了一个边长为4的小正方形,则每个小长方形的面积是( )
A.3 B.6 C.12 D.18
12.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
13.如图,4张边长分别为a、b的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
14.如图,两个正方形边长分别为a、b,如果a+b=8,ab=13,则阴影部分的面积为 .
15.如图,两个正方形边长分别为a、b,如果a+b=8,ab=2,则阴影部分的面积为 .
16.已知a2+ab+b2=7,a2﹣ab+b2=9,则(a+b)2= .
17.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
三.完全平方式
18.若多项式x2+kx+4是一个完全平方式,则k的值是( )
A.2 B.4 C.±2 D.±4
19.已知,x2+kx+9是一个完全平方式,则k的值是( )
A.﹣6 B.3 C.6 D.±6
20.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
21.若4x2﹣(k﹣1)xy+9y2是关于x的完全平方式,则k= .
四.平方差公式
22.3(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )
A.4 B.5 C.6 D.8
23.下列计算中错误的是( )
A.(﹣a﹣b)(b﹣a)=a2﹣b2 B.(﹣a+b)(a﹣b)=a2﹣b2
C.(﹣a﹣b)(﹣b﹣a)=a2+2ab+b2 D.(a+b)2=(a﹣b)2+4ab
24.下列运算中,正确的是( )
A.(a﹣2)2=a2﹣4 B.(a+3)2=a2+9
C.(a﹣1)(a﹣2)=a2﹣3a+2 D.(a﹣2)(2﹣a)=a2﹣4
25.下列各式,不能用平方差公式计算的是( )
A.(a+b﹣1)(a﹣b+1) B.(﹣a﹣b)(﹣a+b)
C.(a+b2)(b2﹣a) D.(2x+y)(x﹣y)
26.下列运算正确的是( )
A.(x+y)(y﹣x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(﹣y+x)=x2﹣y2
27.如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:5=32﹣22,5就是一个智慧数,则下列各数不是智慧数的是( )
A.2020 B.2021 C.2022 D.2023
五.平方差公式的几何背景
28.如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
A.2m+4 B.4m+4 C.m+4 D.2m+2
29.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
30.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
参考答案
一.完全平方公式
1.解:A、(a﹣b)2=a2﹣2ab+b2,故此选项错误;
B、2a+b,无法计算,故此选项错误;
C、(a3)2=a6,故此选项正确;
D、(﹣2a)2=4a4,故此选项错误;
故选:C.
2.解:A.(1+2a)2=1+4a+4a2,故本选项不合题意;
B.a2与a3不是同类项,所以不能合并,故本选项不合题意;
C.(2a3)3=8a9,故本选项不合题意;
D.a3 (﹣a)5=﹣a8,故本选项符合题意;
故选:D.
3.解:∵x+y=6,x2+y2=(x+y)2﹣2xy=20,
∴2xy=62﹣20=16,
∴xy=8,
∴(x﹣y)2=x2+y2﹣2xy=20﹣2×8=4,
∴x﹣y=±2,
故选:D.
4.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
5.解:∵(x﹣y)2=x2﹣2xy+y2,x2+y2=5,xy=2,
∴(x﹣y)2=(x2+y2)﹣2xy
=5﹣2×2
=1,
∴x﹣y=±1,
故答案为:±1.
6.解:∵x﹣y=3,
∴(x﹣y)2=9,
∴x2+y2﹣2xy=9,
∵xy=2,
∴x2+y2﹣2×2=9,
∴x2+y2=13,
故答案为:13.
7.解:因为(x﹣p)2=x2﹣2px+p2,(x﹣p)2=x2+mx+36,
所以m=﹣2p,p2=36,
所以m=﹣2p,p=±6,
所以m=﹣12或12.
故答案为:﹣12或12.
8.解:∵(2020x+2021)2=(2020x)2+2×2021×2020x+20212,
∴c1=20212,
∵(2021x﹣2020)2=(2021x)2﹣2×2020×2021x+20202,
∴c2=20202,
∴c1﹣c2=20212﹣20202=(2021+2020)×(2021﹣2020)=4041,
故答案为:4041.
二.完全平方公式的几何背景
9.解:阴影部分的面积:(a﹣b)2,
还可以表示为:a2﹣2ab+b2,
∴此等式是(a﹣b)2=a2﹣2ab+b2.
故选:A.
10.解:由题意得所剪得的每个小长方形的长为,宽为,
∴中间空余的部分的是一个边长为﹣的正方形,
∴中间空余的部分的面积是()2.
故选:D.
11.解:设小长方形的长为a,宽为b,由图1可得a=3b,
则a﹣b=3b﹣b=2b=4,
解得b=2
∴每个小长方形的面积为,
ab=3b b=3×2 =12,
故选:C.
12.解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
13.解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为a﹣b,则小正方形面积S2=(a﹣b)2,
四个长方形的面积为4ab,
∵S1﹣S2=4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
14.解:根据题意得:
当a+b=8,ab=13时,S阴影=a2﹣b(a﹣b)=a2﹣ab+b2=[(a+b)2﹣2ab]﹣ab==12.5.
故答案为:12.5.
15.解:由题意得阴影部分面积为,
a +b ﹣﹣=﹣+=(a ﹣ab+b )=[(a+b) ﹣3ab],
∴当a+b=8,ab=2时,
阴影部分面积为,
(8 ﹣3×2)=×58=29,
故答案为:29.
16.解:∵a2+ab+b2=7①,a2﹣ab+b2=9②,
∴①+②得:2(a2+b2)=16,即a2+b2=8,
①﹣②得:2ab=﹣2,即ab=﹣1,
则原式=a2+b2+2ab=8﹣2=6,
故答案为:6
17.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2
=(a+b)2﹣2ab﹣(a+b)2
=100﹣40﹣25
=35,
故答案为:35.
三.完全平方式
18.解:∵x2+kx+4是一个完全平方式,
∴kx=±2 x 2,
解得:k=±4,
故选:D.
19.解:∵x2+kx+9是一个完全平方式,
∴kx=±2 x 3,
解得:k=±6,
故选:D.
20.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
21.解:∵4x2﹣(k﹣1)xy+9y2=(2x)2﹣(k﹣1)xy+(3y)2,
∴(k﹣1)xy=±2×2x×3y,
解得k﹣1=±12,
∴k=13,k=﹣11.
故答案为:13或﹣11.
四.平方差公式
22.解:3(22+1)(24+1)(28+1)…(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1…=264﹣1+1=264,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选:C.
23.解:A、原式=(a+b)(a﹣b)=a2﹣b2,故此选项不符合题意;
B、原式=﹣a2+ab+ab﹣b2=﹣a2+2ab﹣b2,故此选项符合题意;
C、原式=(a+b)(a+b)=a2+2ab+b2,故此选项不符合题意;
D、(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a+b)2=(a﹣b)2+4ab,故此选项不符合题意;
故选:B.
24.解:A、(a﹣2)2=a2﹣4a+4,原计算错误,故此选项不符合题意;
B、(a+3)2=a2+6a+9,原计算错误,故此选项不符合题意;
C、(a﹣1)(a﹣2)=a2﹣3a+2,原计算正确,故此选项符合题意;
D、(a﹣2)(2﹣a)=﹣(a﹣2)(a﹣2)=﹣a2+4a﹣4,原计算错误,故此选项不符合题意;
故选:C.
25.解:A、(a+b﹣1)(a﹣b+1)=[a+(b﹣1)][a﹣(b﹣1)],两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
B、(﹣a﹣b)(﹣a+b)=(﹣a+b)(﹣a﹣b),两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
C、(a+b2)(b2﹣a)=(b2+a)(b2﹣a),两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
D、(2x+y)(x﹣y),两数和乘以的不是这两个数的差,不能用平方差公式进行计算,故此选项符合题意;
故选:D.
26.解:A、结果是y2﹣x2,故本选项不符合题意;
B、结果是x2﹣2xy+y2,故本选项不符合题意;
C、结果是x2+2xy+y2,故本选项不符合题意;
D、结果是x2﹣y2,故本选项符合题意;
故选:D.
27.解:设k是正整数,
∵(k+1)2﹣k2=(k+1+k)(k+1﹣k)=2k+1,
∴除1外,所有的奇数都是智慧数,所以,B,D选项都是智慧数,不符合题意;
∵(k+1)2﹣(k﹣1)2=(k+1+k﹣1)(k+1﹣k+1)=4k,
∴除4外,所有的能被4整除的偶数都是智慧数,所以A选项是智慧数,不符合题意,
C选项2022不是奇数也不是4的倍数,不是智慧数,符合题意.
故选:C.
五.平方差公式的几何背景
28.解:依题意得剩余部分为
(m+2)2﹣m2=m2+4m+4﹣m2=4m+4,
而拼成的矩形一边长为2,
∴另一边长是(4m+4)÷2=2m+2.
∴面积为2(2m+2)=4m+4.
故选:B.
29.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
30.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
知识点分类训练(附答案)
一.完全平方公式
1.下列运算正确的是( )
A.(a﹣b)2=a2﹣b2 B.2a+b=2ab
C.(a3)2=a6 D.(﹣2a)2=﹣4a4
2.下列运算正确的是( )
A.(1+2a)2=1+2a+4a2 B.a2+a3=a5
C.(2a3)3=6a9 D.a3 (﹣a)5=﹣a8
3.若x+y=6,x2+y2=20,求x﹣y的值是( )
A.2 B.﹣2 C.4 D.±2
4.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
5.若x2+y2=5,xy=2,则x﹣y= .
6.若x﹣y=3,xy=2,则x2+y2= .
7.已知(x﹣p)2=x2+mx+36,则m= .
8.小明将(2020x+2021)2展开后得到a1x2+b1x+c1;小红将(2021x﹣2020)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则c1﹣c2的值是 .
二.完全平方公式的几何背景
9.我们已经接触了很多代数恒等式,知道可以用一些硬纸片拼成的图形的面积来解释一些代数恒等式,例如图1可以用来解(a+b)2﹣(a﹣b)2=4ab,那么通过图2中阴影部分面积的计算验证的恒等式是( )
A.(a﹣b)2=a2﹣2ab+b2
B.a2﹣b2=(a+b)(a﹣b)
C.(a+b)2=a2+2ab+b2
D.(a﹣b)(a+2b)=a2+ab﹣2b2
10.图(1)是一个长为a,宽为b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是( )
A.a2 B.b2 C.(a﹣b)2 D.(a﹣b)2
11.现有四个大小相同的长方形,可拼成如图1和图2所示的图形,在拼图2时,中间留下了一个边长为4的小正方形,则每个小长方形的面积是( )
A.3 B.6 C.12 D.18
12.如图,两个正方形的边长分别为a和b,如果a﹣b=2,ab=26,那么阴影部分的面积是( )
A.30 B.34 C.40 D.44
13.如图,4张边长分别为a、b的长方形纸片围成一个正方形,从中可以得到的等式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.(a+b)2﹣(a﹣b)2=4ab
14.如图,两个正方形边长分别为a、b,如果a+b=8,ab=13,则阴影部分的面积为 .
15.如图,两个正方形边长分别为a、b,如果a+b=8,ab=2,则阴影部分的面积为 .
16.已知a2+ab+b2=7,a2﹣ab+b2=9,则(a+b)2= .
17.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
三.完全平方式
18.若多项式x2+kx+4是一个完全平方式,则k的值是( )
A.2 B.4 C.±2 D.±4
19.已知,x2+kx+9是一个完全平方式,则k的值是( )
A.﹣6 B.3 C.6 D.±6
20.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
21.若4x2﹣(k﹣1)xy+9y2是关于x的完全平方式,则k= .
四.平方差公式
22.3(22+1)(24+1)(28+1)…(232+1)+1的个位数是( )
A.4 B.5 C.6 D.8
23.下列计算中错误的是( )
A.(﹣a﹣b)(b﹣a)=a2﹣b2 B.(﹣a+b)(a﹣b)=a2﹣b2
C.(﹣a﹣b)(﹣b﹣a)=a2+2ab+b2 D.(a+b)2=(a﹣b)2+4ab
24.下列运算中,正确的是( )
A.(a﹣2)2=a2﹣4 B.(a+3)2=a2+9
C.(a﹣1)(a﹣2)=a2﹣3a+2 D.(a﹣2)(2﹣a)=a2﹣4
25.下列各式,不能用平方差公式计算的是( )
A.(a+b﹣1)(a﹣b+1) B.(﹣a﹣b)(﹣a+b)
C.(a+b2)(b2﹣a) D.(2x+y)(x﹣y)
26.下列运算正确的是( )
A.(x+y)(y﹣x)=x2﹣y2 B.(﹣x+y)2=﹣x2+2xy+y2
C.(﹣x﹣y)2=﹣x2﹣2xy﹣y2 D.(x+y)(﹣y+x)=x2﹣y2
27.如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:5=32﹣22,5就是一个智慧数,则下列各数不是智慧数的是( )
A.2020 B.2021 C.2022 D.2023
五.平方差公式的几何背景
28.如图,边长为(m+2)的正方形纸片剪出一个边长为m的正方形之后余下部分又剪开拼成一个长方形(不重叠无缝隙),若拼成的长方形一边长为2,其面积是( )
A.2m+4 B.4m+4 C.m+4 D.2m+2
29.如图1,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图2),利用这两个图形的面积,可以验证的等式是( )
A.a2+b2=(a+b)(a﹣b) B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)2=a2+2ab+b2 D.a2﹣b2=(a+b)(a﹣b)
30.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是 .
参考答案
一.完全平方公式
1.解:A、(a﹣b)2=a2﹣2ab+b2,故此选项错误;
B、2a+b,无法计算,故此选项错误;
C、(a3)2=a6,故此选项正确;
D、(﹣2a)2=4a4,故此选项错误;
故选:C.
2.解:A.(1+2a)2=1+4a+4a2,故本选项不合题意;
B.a2与a3不是同类项,所以不能合并,故本选项不合题意;
C.(2a3)3=8a9,故本选项不合题意;
D.a3 (﹣a)5=﹣a8,故本选项符合题意;
故选:D.
3.解:∵x+y=6,x2+y2=(x+y)2﹣2xy=20,
∴2xy=62﹣20=16,
∴xy=8,
∴(x﹣y)2=x2+y2﹣2xy=20﹣2×8=4,
∴x﹣y=±2,
故选:D.
4.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
5.解:∵(x﹣y)2=x2﹣2xy+y2,x2+y2=5,xy=2,
∴(x﹣y)2=(x2+y2)﹣2xy
=5﹣2×2
=1,
∴x﹣y=±1,
故答案为:±1.
6.解:∵x﹣y=3,
∴(x﹣y)2=9,
∴x2+y2﹣2xy=9,
∵xy=2,
∴x2+y2﹣2×2=9,
∴x2+y2=13,
故答案为:13.
7.解:因为(x﹣p)2=x2﹣2px+p2,(x﹣p)2=x2+mx+36,
所以m=﹣2p,p2=36,
所以m=﹣2p,p=±6,
所以m=﹣12或12.
故答案为:﹣12或12.
8.解:∵(2020x+2021)2=(2020x)2+2×2021×2020x+20212,
∴c1=20212,
∵(2021x﹣2020)2=(2021x)2﹣2×2020×2021x+20202,
∴c2=20202,
∴c1﹣c2=20212﹣20202=(2021+2020)×(2021﹣2020)=4041,
故答案为:4041.
二.完全平方公式的几何背景
9.解:阴影部分的面积:(a﹣b)2,
还可以表示为:a2﹣2ab+b2,
∴此等式是(a﹣b)2=a2﹣2ab+b2.
故选:A.
10.解:由题意得所剪得的每个小长方形的长为,宽为,
∴中间空余的部分的是一个边长为﹣的正方形,
∴中间空余的部分的面积是()2.
故选:D.
11.解:设小长方形的长为a,宽为b,由图1可得a=3b,
则a﹣b=3b﹣b=2b=4,
解得b=2
∴每个小长方形的面积为,
ab=3b b=3×2 =12,
故选:C.
12.解:如图,
∵a﹣b=2,ab=26,
∴a2﹣2ab+b2=4,
∴a2+b2=4+2ab=4+52=56,
阴影部分的面积=S△ABC+S△CDM+S△AEF+S△GHM
=2×(a﹣b)×a+2×b×b
=a(a﹣b)+b2
=a2+b2﹣ab
=56﹣26
=30.
故选:A.
13.解:设大正方形的面积S1,小正方形的面积S2,
大正方形的边长为a+b,则大正方形面积S1=(a+b)2,
小正方形的边长为a﹣b,则小正方形面积S2=(a﹣b)2,
四个长方形的面积为4ab,
∵S1﹣S2=4ab,
∴(a+b)2﹣(a﹣b)2=4ab,
故选:D.
14.解:根据题意得:
当a+b=8,ab=13时,S阴影=a2﹣b(a﹣b)=a2﹣ab+b2=[(a+b)2﹣2ab]﹣ab==12.5.
故答案为:12.5.
15.解:由题意得阴影部分面积为,
a +b ﹣﹣=﹣+=(a ﹣ab+b )=[(a+b) ﹣3ab],
∴当a+b=8,ab=2时,
阴影部分面积为,
(8 ﹣3×2)=×58=29,
故答案为:29.
16.解:∵a2+ab+b2=7①,a2﹣ab+b2=9②,
∴①+②得:2(a2+b2)=16,即a2+b2=8,
①﹣②得:2ab=﹣2,即ab=﹣1,
则原式=a2+b2+2ab=8﹣2=6,
故答案为:6
17.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2
=(a+b)2﹣2ab﹣(a+b)2
=100﹣40﹣25
=35,
故答案为:35.
三.完全平方式
18.解:∵x2+kx+4是一个完全平方式,
∴kx=±2 x 2,
解得:k=±4,
故选:D.
19.解:∵x2+kx+9是一个完全平方式,
∴kx=±2 x 3,
解得:k=±6,
故选:D.
20.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
21.解:∵4x2﹣(k﹣1)xy+9y2=(2x)2﹣(k﹣1)xy+(3y)2,
∴(k﹣1)xy=±2×2x×3y,
解得k﹣1=±12,
∴k=13,k=﹣11.
故答案为:13或﹣11.
四.平方差公式
22.解:3(22+1)(24+1)(28+1)…(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1…=264﹣1+1=264,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵64÷4=16,
∴264个位上数字为6,即原式个位上数字为6.
故选:C.
23.解:A、原式=(a+b)(a﹣b)=a2﹣b2,故此选项不符合题意;
B、原式=﹣a2+ab+ab﹣b2=﹣a2+2ab﹣b2,故此选项符合题意;
C、原式=(a+b)(a+b)=a2+2ab+b2,故此选项不符合题意;
D、(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a+b)2=(a﹣b)2+4ab,故此选项不符合题意;
故选:B.
24.解:A、(a﹣2)2=a2﹣4a+4,原计算错误,故此选项不符合题意;
B、(a+3)2=a2+6a+9,原计算错误,故此选项不符合题意;
C、(a﹣1)(a﹣2)=a2﹣3a+2,原计算正确,故此选项符合题意;
D、(a﹣2)(2﹣a)=﹣(a﹣2)(a﹣2)=﹣a2+4a﹣4,原计算错误,故此选项不符合题意;
故选:C.
25.解:A、(a+b﹣1)(a﹣b+1)=[a+(b﹣1)][a﹣(b﹣1)],两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
B、(﹣a﹣b)(﹣a+b)=(﹣a+b)(﹣a﹣b),两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
C、(a+b2)(b2﹣a)=(b2+a)(b2﹣a),两数和乘以这两个数的差,能用平方差公式进行计算,故此选项不符合题意;
D、(2x+y)(x﹣y),两数和乘以的不是这两个数的差,不能用平方差公式进行计算,故此选项符合题意;
故选:D.
26.解:A、结果是y2﹣x2,故本选项不符合题意;
B、结果是x2﹣2xy+y2,故本选项不符合题意;
C、结果是x2+2xy+y2,故本选项不符合题意;
D、结果是x2﹣y2,故本选项符合题意;
故选:D.
27.解:设k是正整数,
∵(k+1)2﹣k2=(k+1+k)(k+1﹣k)=2k+1,
∴除1外,所有的奇数都是智慧数,所以,B,D选项都是智慧数,不符合题意;
∵(k+1)2﹣(k﹣1)2=(k+1+k﹣1)(k+1﹣k+1)=4k,
∴除4外,所有的能被4整除的偶数都是智慧数,所以A选项是智慧数,不符合题意,
C选项2022不是奇数也不是4的倍数,不是智慧数,符合题意.
故选:C.
五.平方差公式的几何背景
28.解:依题意得剩余部分为
(m+2)2﹣m2=m2+4m+4﹣m2=4m+4,
而拼成的矩形一边长为2,
∴另一边长是(4m+4)÷2=2m+2.
∴面积为2(2m+2)=4m+4.
故选:B.
29.解:∵图1中的阴影部分面积为:a2﹣b2,图2中阴影部分面积为:(2b+2a)(a﹣b),
∴a2﹣b2=(2b+2a)(a﹣b),即a2﹣b2=(a+b)(a﹣b),
故选:D.
30.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得a2﹣b2=40,
∴(a+b)(a﹣b)=40;
∵S阴=S△ACD﹣S△CDE,
∴S阴=×CD×AB﹣×CD×BE
=(a+b)a﹣(a+b)b
=(a+b)(a﹣b)
∵(a+b)(a﹣b)=40,
∴S阴=×40
=20.
故答案为:20.
