2021—2022学年人教版九年级数学下册27.2相似三角形 同步练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.2相似三角形 同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 277.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 19:26:06 | ||
图片预览




文档简介
初中数学九年级下人教版27.2相似三角形
一、选择题(共18题)
如图, 是等腰直角三角形,,以斜边 上的点 为圆心的圆分别与 , 相切于点 ,,与 分别相交于点 ,,且 的延长线与 的延长线交于点 ,则 的长为
A. B. C. D.
将直角三角形的三条边长同时扩大同一倍数,得到的三角形是
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
如图,在 中,,,.点 为边 上的动点,作菱形 ,使点 , 在边 上,点 在边 上.若这样的菱形能作出 个,则 的取值范围是
A. B. C. D.
如图,已知点 , 分别在反比例函数 , 的图象上,且 ,则 的值为
A. B. C. D.
如图,已知 , 分别为正方形 的边 , 的中点, 与 交于点 , 为 的中点,则下列结论:
① ;
② ;
③ ;
④ ;
⑤ .
其中正确结论的是
A.①③④ B.②④⑤ C.①③④⑤ D.①③⑤
如图,在平行四边形 中,,, 的平分线交 于 ,交 的延长线于 , 于 ,,则 的周长为
A. B. C. D.
如图,矩形 的顶点 , 都在坐标轴上,点 在第二象限,矩形 的面积为 .把矩形 沿 翻折,使点 与点 重合.若反比例函数 的图象恰好经过点 和 的中点 .则 的长为
A. B. C. D.
如图,将矩形 沿 折叠,使点 落在 边的点 处,过点 作 交 于点 ,连接 .给出以下结论:① ;②四边形 是菱形;③ ;④当 , 时, 的长为 ,其中正确的结论个数是
A. B. C. D.
如图,电灯 在横杆 的正上方, 在灯光下的影子为 ,,,,点 到 的距离是 ,则点 到 的距离是
A. B. C. D.
如图,在 中,,, 平分 交 于 , 于 ,则下列结论:① ;② ;③ ;④若 为 中点,则 ,其中正确的结论有
A. 个 B. 个 C. 个 D. 个
如图,正方形 的边长是 ,点 , 分别是 , 延长线上的点且 ,连接 , 交于点 ,并分别与边 , 交于点 ,,连接 ,下列结论:;;; 当 时,,其中正确结论的个数为
A. 个 B. 个 C. 个 D. 个
如图,矩形 ,,,点 , 分别为边 和边 上的两点,且 ,点 是点 关于 所在的直线的对称点,取 的中点 ,连接 ,,分别将 沿着 所在的直线折叠,将 沿着 所在的直线折叠,点 和点 恰好重合于 上的点 .以下结论中:
① ;
② ;
③ ;
④四边形 是正方形;
⑤ .
其中正确的结论是
A.①② B.①④ C.①③⑤ D.①④⑤
如图, 是 的平分线,,,若 ,,则 的长为
A. B. C. D.
在 与 中,下列四个命题是真命题的个数共有
①如果 ,,那么 与 相似;
②如果 ,,那么 与 相似;
③如果 ,,那么 与 相似;
④如果 ,,那么那么 与 相似.
A. 个 B. 个 C. 个 D. 个
如图,在平行四边形 中, 为 边上的中点, 交 于点 ,若 ,则平行四边形 的面积为
A. B. C. D.
如图,,,点 在边 上(与 , 不重合),四边形 为正方形,过点 作 ,交 的延长线于点 ,连接 ,交 于点 ,给出以下结论:
① ;
② ;
③ ;
④如果 ,,则 .
其中正确的结论的个数是
A. B. C. D.
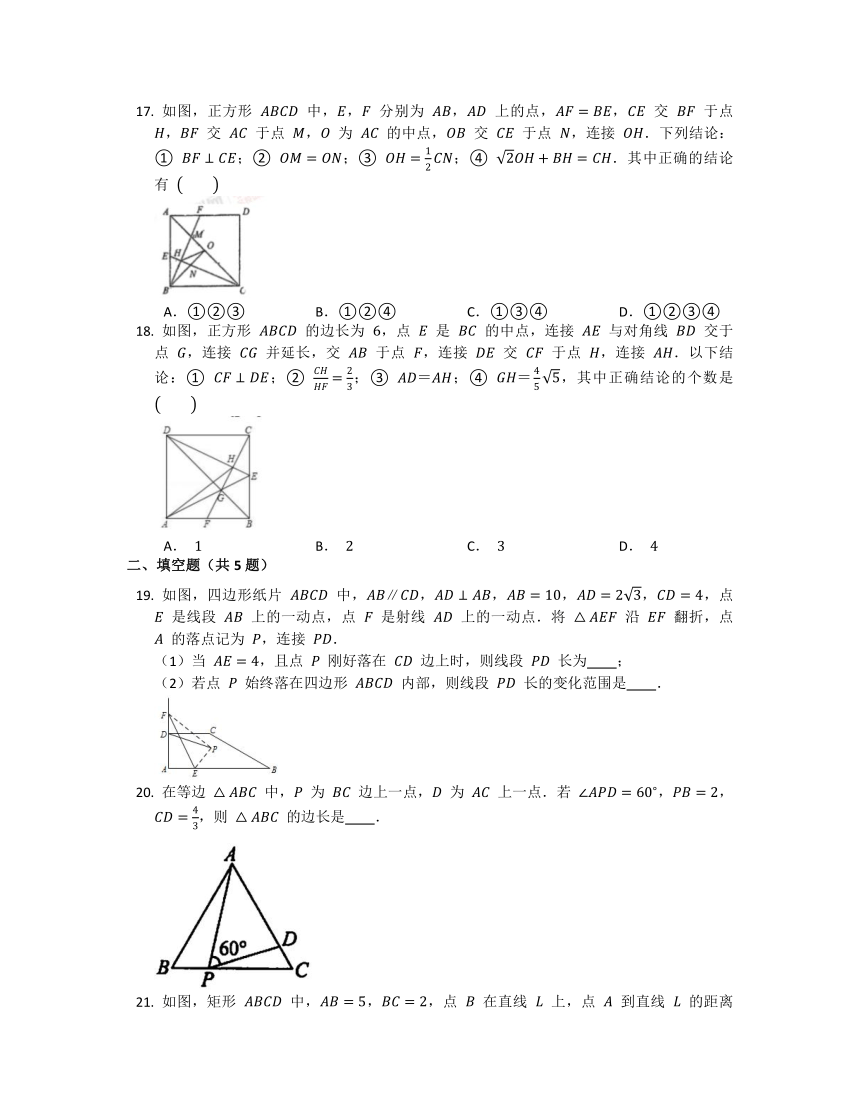
如图,正方形 中,, 分别为 , 上的点,, 交 于点 , 交 于点 , 为 的中点, 交 于点 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有
A.①②③ B.①②④ C.①③④ D.①②③④
如图,正方形 的边长为 ,点 是 的中点,连接 与对角线 交于点 ,连接 并延长,交 于点 ,连接 交 于点 ,连接 .以下结论:① ;② ;③ ;④ ,其中正确结论的个数是
A. B. C. D.
二、填空题(共5题)
如图,四边形纸片 中,,,,,,点 是线段 上的一动点,点 是射线 上的一动点.将 沿 翻折,点 的落点记为 ,连接 .
(1)当 ,且点 刚好落在 边上时,则线段 长为 ;
(2)若点 始终落在四边形 内部,则线段 长的变化范围是 .
在等边 中, 为 边上一点, 为 上一点.若 ,,,则 的边长是 .
如图,矩形 中,,,点 在直线 上,点 到直线 的距离 ,则点 到直线 的距离 为 .
如图,在平行四边形 中,,,,点 为边 上的一个动点,连接 并延长至点 ,使得 ,以 , 为邻边构造平行四边形 ,连接 ,则 的最小值为 .
如图,边长为 的正方形 的对角线 与 交于点 ,将正方形 沿直线 折叠,点 落在对角线 的点 处,折痕 交 于点 ,交 于点 ,则 的长为 .
三、解答题(共5题)
如图,在 中,,,,点 在 上,且 ,现有两个动点 , 分别从点 和点 同时出发,其中点 以 的速度沿 向终点 运动;点 以 的速度沿 向终点 运动.过点 作 交 于点 ,连接 .设动点运动的时间为 .
(1) 连接 ,当 时,四边形 能够成为平行四边形吗?请说明理由.
(2) 连接 ,在运动的过程中,不论 取何值时,总有线段 与线段 平行,为什么?
(3) 当 为何值时, 为直角三角形?
如图,直线 交坐标轴于 , 两点,直线 交 轴于点 ,抛物线恰好过点 ,,.
(1) 求抛物线的表达式;
(2) 当点 在线段 上方的曲线上移动时,求四边形 的面积的最大值;
(3) 点 在抛物线的对称轴上,点 在抛物线上,是否存在点 使得以 ,,, 为顶点的四边形是平行四边形?若存在求出点 坐标;若不存在,说明理由.
在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 ,连接 ,以点 为中心,顺时针旋转矩形 ,旋转角为 ,得到矩形 ,点 ,, 的对应点分别为 ,,.
(1) 如图,当点 落在对角线 上时,求点 的坐标;
(2) 在(Ⅰ)的情况下, 与 交于点 .
①求证 ;
②求点 的坐标;
(3) 为何值时,(直接写出结果即可).
如图, 中,,, 平分 ,交 轴于点 ,点 是 轴上一点, 经过点 ,,与 轴交于点 ,过点 作 ,垂足为 , 的延长线交 轴于点 .
(1) 求证: 为 的切线;
(2) 求 的半径.
如图,在 中,,,点 从点 开始沿 边向点 以每秒 的速度移动,点 从点 开始沿 边向点 以每秒 的速度移动.如果 , 分别从 , 同时出发,经过几秒 与 相似?
答案
一、选择题(共18题)
1.B
2.C
3.B
4.A
5.C
6.D
7.D
8.D
9.C
10.D
11.C
12.B
13.A
14.C
15.D
16.D
17.B
18.D
二、填空题(共5题)
19.;
20.
21.
22.
23.
三、解答题(共5题)
24.
(1) 能.理由如下:
当 时,,.
.
,
.
,即 .
.
.
四边形 是平行四边形.
(2) ,,,.
,,
.
又 ,
.
.
.
(3) 当 时,,
.
,解得 .
当 时,,
.
,
.
,即 .
,.
,解得 .
当 为 或 时, 为直角三角形.
25.
(1) 直线 交 轴于 , 两点,
,
由 得,.
.
.
又 在 轴负半轴上,
.
设抛物线解析式 .
把 ,, 代入上式得
解得
抛物线解析式为 .
(2) 如图 ,过点 作 轴,交直线 与点 .
设 点横坐标为 ,则 ,.
.
.
.
故当 时, 的面积最大,为 .
(3) 存在.
如图 ,
当 , 在对称轴左侧时,可以看作把 沿水平向右平移至 与对称轴重合时,再将其向上平移,恰好使点 与点 重合,点 与点 重合.
此时四边形 为平行四边形.
.
点 的横坐标为,.
当 时,.
即此时 .
如图 ,
当 , 在对称轴右侧时,把 绕点 旋转 恰好与抛物线相交于 ,则四边形 为平行四边形.
此时易得 点纵坐标为,.
当 时,.
解得,(舍去)或 .
此时 .
如图 ,
以线段 为对角线作平行四边形 ,过 作 垂直于对称轴直线于点 .
过点 作 轴交于点 .
.
又 ,
.
点坐标为 .
当 时,.
此时 .
综上所述,满足题意的 点坐标有 ,,.
26.
(1) 如图 ,过 作 于 ,
点 ,点 ,
,,
四边形 是矩形,
,,
,
,
,
设 ,,
,
由旋转得:,
由勾股定理得:,,
解得:(舍),,
,,
.
(2) ①由旋转得:,
,
,
,
,
,
,
,,
,
在 和 中,
;
② ,
,
,
设 ,则 ,,
在 中,由勾股定理得:,
,,
,
.
(3) 为 或 时,.
27.
(1) 连接 .
,
,
平分 ,
,
,
,
,
,即 是 的切线.
(2) 平分 ,
,
,
,
,
,
,
,
,,
,,
,
,
,
的半径为 .
28.设经过 两三角形相似,
则 ,.
①当 与 是对应边时,
,
,即 ,
解得 .
②当 与 是对应边时,
,
,即 ,解得 .
综上所述,经过 或 , 与 相似.
一、选择题(共18题)
如图, 是等腰直角三角形,,以斜边 上的点 为圆心的圆分别与 , 相切于点 ,,与 分别相交于点 ,,且 的延长线与 的延长线交于点 ,则 的长为
A. B. C. D.
将直角三角形的三条边长同时扩大同一倍数,得到的三角形是
A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形
如图,在 中,,,.点 为边 上的动点,作菱形 ,使点 , 在边 上,点 在边 上.若这样的菱形能作出 个,则 的取值范围是
A. B. C. D.
如图,已知点 , 分别在反比例函数 , 的图象上,且 ,则 的值为
A. B. C. D.
如图,已知 , 分别为正方形 的边 , 的中点, 与 交于点 , 为 的中点,则下列结论:
① ;
② ;
③ ;
④ ;
⑤ .
其中正确结论的是
A.①③④ B.②④⑤ C.①③④⑤ D.①③⑤
如图,在平行四边形 中,,, 的平分线交 于 ,交 的延长线于 , 于 ,,则 的周长为
A. B. C. D.
如图,矩形 的顶点 , 都在坐标轴上,点 在第二象限,矩形 的面积为 .把矩形 沿 翻折,使点 与点 重合.若反比例函数 的图象恰好经过点 和 的中点 .则 的长为
A. B. C. D.
如图,将矩形 沿 折叠,使点 落在 边的点 处,过点 作 交 于点 ,连接 .给出以下结论:① ;②四边形 是菱形;③ ;④当 , 时, 的长为 ,其中正确的结论个数是
A. B. C. D.
如图,电灯 在横杆 的正上方, 在灯光下的影子为 ,,,,点 到 的距离是 ,则点 到 的距离是
A. B. C. D.
如图,在 中,,, 平分 交 于 , 于 ,则下列结论:① ;② ;③ ;④若 为 中点,则 ,其中正确的结论有
A. 个 B. 个 C. 个 D. 个
如图,正方形 的边长是 ,点 , 分别是 , 延长线上的点且 ,连接 , 交于点 ,并分别与边 , 交于点 ,,连接 ,下列结论:;;; 当 时,,其中正确结论的个数为
A. 个 B. 个 C. 个 D. 个
如图,矩形 ,,,点 , 分别为边 和边 上的两点,且 ,点 是点 关于 所在的直线的对称点,取 的中点 ,连接 ,,分别将 沿着 所在的直线折叠,将 沿着 所在的直线折叠,点 和点 恰好重合于 上的点 .以下结论中:
① ;
② ;
③ ;
④四边形 是正方形;
⑤ .
其中正确的结论是
A.①② B.①④ C.①③⑤ D.①④⑤
如图, 是 的平分线,,,若 ,,则 的长为
A. B. C. D.
在 与 中,下列四个命题是真命题的个数共有
①如果 ,,那么 与 相似;
②如果 ,,那么 与 相似;
③如果 ,,那么 与 相似;
④如果 ,,那么那么 与 相似.
A. 个 B. 个 C. 个 D. 个
如图,在平行四边形 中, 为 边上的中点, 交 于点 ,若 ,则平行四边形 的面积为
A. B. C. D.
如图,,,点 在边 上(与 , 不重合),四边形 为正方形,过点 作 ,交 的延长线于点 ,连接 ,交 于点 ,给出以下结论:
① ;
② ;
③ ;
④如果 ,,则 .
其中正确的结论的个数是
A. B. C. D.
如图,正方形 中,, 分别为 , 上的点,, 交 于点 , 交 于点 , 为 的中点, 交 于点 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有
A.①②③ B.①②④ C.①③④ D.①②③④
如图,正方形 的边长为 ,点 是 的中点,连接 与对角线 交于点 ,连接 并延长,交 于点 ,连接 交 于点 ,连接 .以下结论:① ;② ;③ ;④ ,其中正确结论的个数是
A. B. C. D.
二、填空题(共5题)
如图,四边形纸片 中,,,,,,点 是线段 上的一动点,点 是射线 上的一动点.将 沿 翻折,点 的落点记为 ,连接 .
(1)当 ,且点 刚好落在 边上时,则线段 长为 ;
(2)若点 始终落在四边形 内部,则线段 长的变化范围是 .
在等边 中, 为 边上一点, 为 上一点.若 ,,,则 的边长是 .
如图,矩形 中,,,点 在直线 上,点 到直线 的距离 ,则点 到直线 的距离 为 .
如图,在平行四边形 中,,,,点 为边 上的一个动点,连接 并延长至点 ,使得 ,以 , 为邻边构造平行四边形 ,连接 ,则 的最小值为 .
如图,边长为 的正方形 的对角线 与 交于点 ,将正方形 沿直线 折叠,点 落在对角线 的点 处,折痕 交 于点 ,交 于点 ,则 的长为 .
三、解答题(共5题)
如图,在 中,,,,点 在 上,且 ,现有两个动点 , 分别从点 和点 同时出发,其中点 以 的速度沿 向终点 运动;点 以 的速度沿 向终点 运动.过点 作 交 于点 ,连接 .设动点运动的时间为 .
(1) 连接 ,当 时,四边形 能够成为平行四边形吗?请说明理由.
(2) 连接 ,在运动的过程中,不论 取何值时,总有线段 与线段 平行,为什么?
(3) 当 为何值时, 为直角三角形?
如图,直线 交坐标轴于 , 两点,直线 交 轴于点 ,抛物线恰好过点 ,,.
(1) 求抛物线的表达式;
(2) 当点 在线段 上方的曲线上移动时,求四边形 的面积的最大值;
(3) 点 在抛物线的对称轴上,点 在抛物线上,是否存在点 使得以 ,,, 为顶点的四边形是平行四边形?若存在求出点 坐标;若不存在,说明理由.
在平面直角坐标系中,四边形 是矩形,点 ,点 ,点 ,连接 ,以点 为中心,顺时针旋转矩形 ,旋转角为 ,得到矩形 ,点 ,, 的对应点分别为 ,,.
(1) 如图,当点 落在对角线 上时,求点 的坐标;
(2) 在(Ⅰ)的情况下, 与 交于点 .
①求证 ;
②求点 的坐标;
(3) 为何值时,(直接写出结果即可).
如图, 中,,, 平分 ,交 轴于点 ,点 是 轴上一点, 经过点 ,,与 轴交于点 ,过点 作 ,垂足为 , 的延长线交 轴于点 .
(1) 求证: 为 的切线;
(2) 求 的半径.
如图,在 中,,,点 从点 开始沿 边向点 以每秒 的速度移动,点 从点 开始沿 边向点 以每秒 的速度移动.如果 , 分别从 , 同时出发,经过几秒 与 相似?
答案
一、选择题(共18题)
1.B
2.C
3.B
4.A
5.C
6.D
7.D
8.D
9.C
10.D
11.C
12.B
13.A
14.C
15.D
16.D
17.B
18.D
二、填空题(共5题)
19.;
20.
21.
22.
23.
三、解答题(共5题)
24.
(1) 能.理由如下:
当 时,,.
.
,
.
,即 .
.
.
四边形 是平行四边形.
(2) ,,,.
,,
.
又 ,
.
.
.
(3) 当 时,,
.
,解得 .
当 时,,
.
,
.
,即 .
,.
,解得 .
当 为 或 时, 为直角三角形.
25.
(1) 直线 交 轴于 , 两点,
,
由 得,.
.
.
又 在 轴负半轴上,
.
设抛物线解析式 .
把 ,, 代入上式得
解得
抛物线解析式为 .
(2) 如图 ,过点 作 轴,交直线 与点 .
设 点横坐标为 ,则 ,.
.
.
.
故当 时, 的面积最大,为 .
(3) 存在.
如图 ,
当 , 在对称轴左侧时,可以看作把 沿水平向右平移至 与对称轴重合时,再将其向上平移,恰好使点 与点 重合,点 与点 重合.
此时四边形 为平行四边形.
.
点 的横坐标为,.
当 时,.
即此时 .
如图 ,
当 , 在对称轴右侧时,把 绕点 旋转 恰好与抛物线相交于 ,则四边形 为平行四边形.
此时易得 点纵坐标为,.
当 时,.
解得,(舍去)或 .
此时 .
如图 ,
以线段 为对角线作平行四边形 ,过 作 垂直于对称轴直线于点 .
过点 作 轴交于点 .
.
又 ,
.
点坐标为 .
当 时,.
此时 .
综上所述,满足题意的 点坐标有 ,,.
26.
(1) 如图 ,过 作 于 ,
点 ,点 ,
,,
四边形 是矩形,
,,
,
,
,
设 ,,
,
由旋转得:,
由勾股定理得:,,
解得:(舍),,
,,
.
(2) ①由旋转得:,
,
,
,
,
,
,
,,
,
在 和 中,
;
② ,
,
,
设 ,则 ,,
在 中,由勾股定理得:,
,,
,
.
(3) 为 或 时,.
27.
(1) 连接 .
,
,
平分 ,
,
,
,
,
,即 是 的切线.
(2) 平分 ,
,
,
,
,
,
,
,
,,
,,
,
,
,
的半径为 .
28.设经过 两三角形相似,
则 ,.
①当 与 是对应边时,
,
,即 ,
解得 .
②当 与 是对应边时,
,
,即 ,解得 .
综上所述,经过 或 , 与 相似.
