2021-2022学年人教版数学九年级下册28.2解直角三角形及其应用同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册28.2解直角三角形及其应用同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 666.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览


文档简介
初中数学九年级下人教版28.2解直角三角形及其应用
一、选择题(共20题)
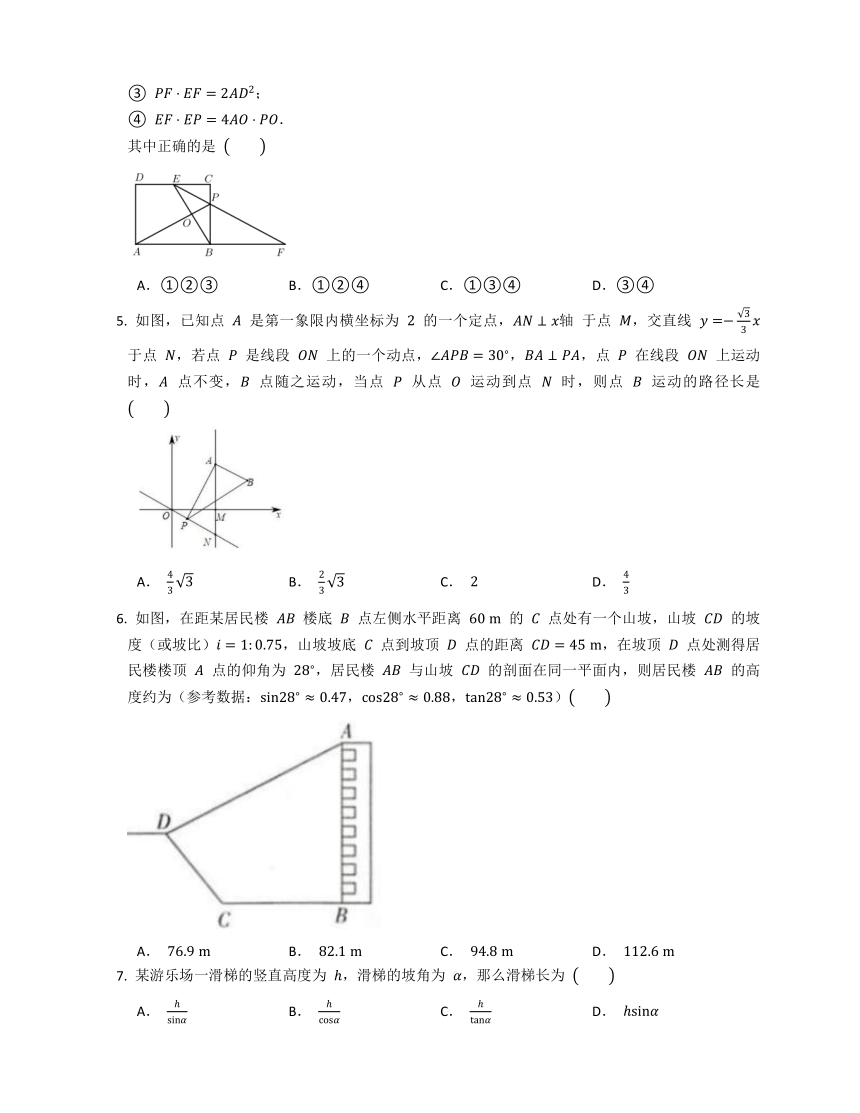
数学活动课上,小敏、小颖分别画了 和 ,尺寸如图.如果两个三角形的面积分别记作 ,,那么它们的大小关系是
A. B. C. D.不能确定
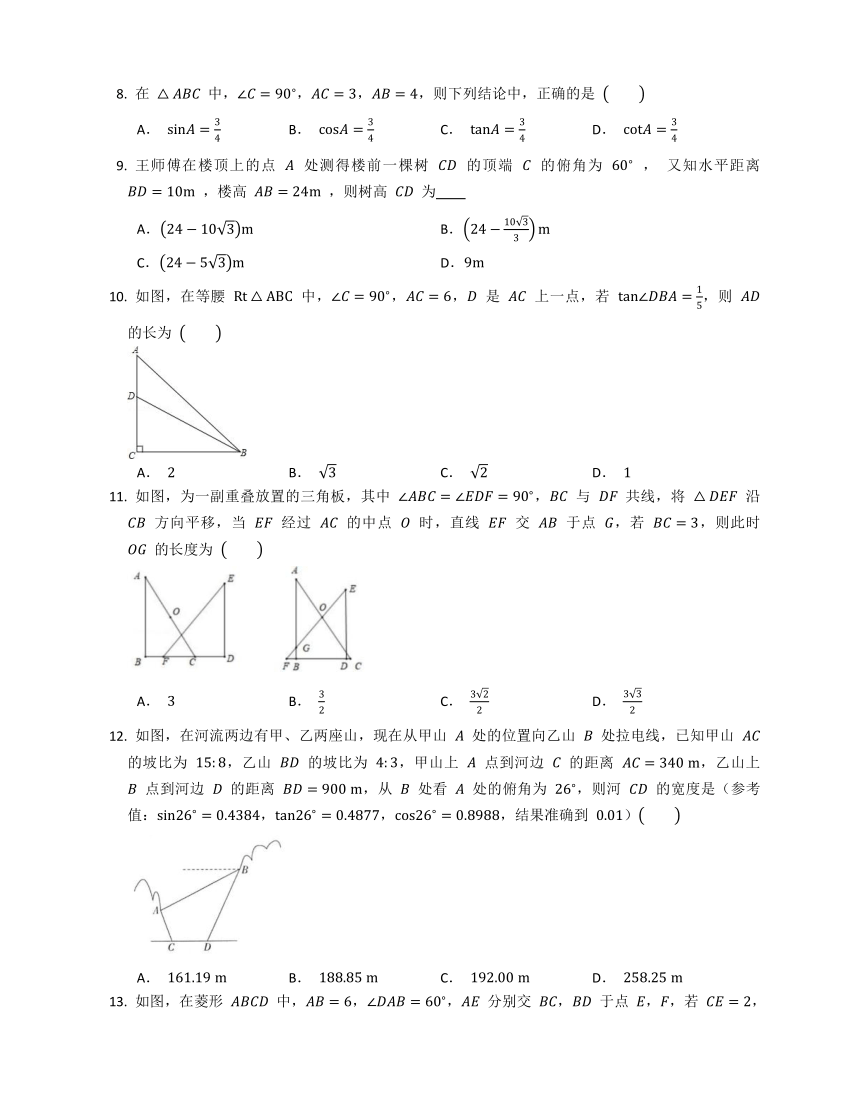
如图, 中,,, 所对的三边分别记为 ,,, 是 的外心,,,,则 等于
A. B.
C. D.
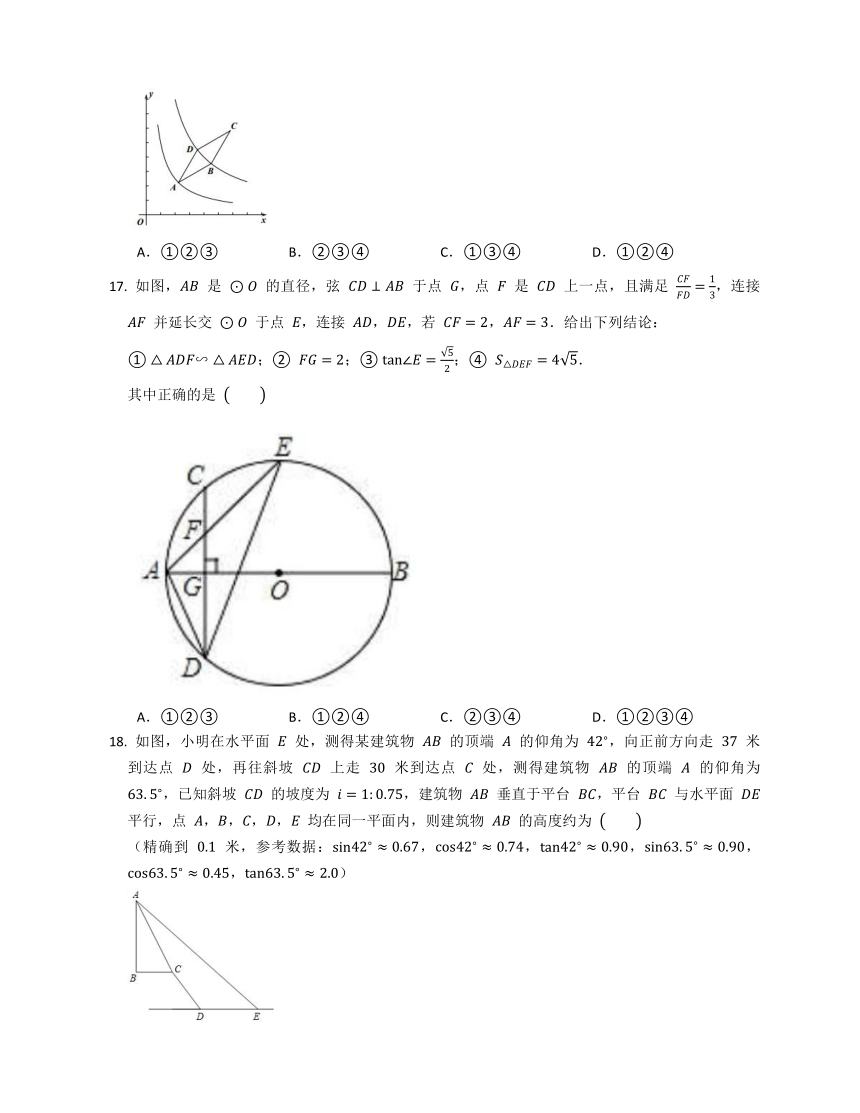
如图,一电线杆 的高为 米,当太阳光线与地面的夹角为 时,其影长 约为 ( 取 ,结果精确到 米)
A. 米 B. 米 C. 米 D. 米
如图,矩形 中, 为 的中点,,,连接 并延长,交 的延长线于点 ,, 相交于点 .下列结论:
① 平分 ;
② ;
③ ;
④ .
其中正确的是
A.①②③ B.①②④ C.①③④ D.③④
如图,已知点 是第一象限内横坐标为 的一个定点, 于点 ,交直线 于点 ,若点 是线段 上的一个动点,,,点 在线段 上运动时, 点不变, 点随之运动,当点 从点 运动到点 时,则点 运动的路径长是
A. B. C. D.
如图,在距某居民楼 楼底 点左侧水平距离 的 点处有一个山坡,山坡 的坡度(或坡比),山坡坡底 点到坡顶 点的距离 ,在坡顶 点处测得居民楼楼顶 点的仰角为 ,居民楼 与山坡 的剖面在同一平面内,则居民楼 的高度约为(参考数据:,,)
A. B. C. D.
某游乐场一滑梯的竖直高度为 ,滑梯的坡角为 ,那么滑梯长为
A. B. C. D.
在 中,,,,则下列结论中,正确的是
A. B. C. D.
王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 , 又知水平距离 ,楼高 ,则树高 为
A. B.
C. D.
如图,在等腰 中,,, 是 上一点,若 ,则 的长为
A. B. C. D.
如图,为一副重叠放置的三角板,其中 , 与 共线,将 沿 方向平移,当 经过 的中点 时,直线 交 于点 ,若 ,则此时 的长度为
A. B. C. D.
如图,在河流两边有甲、乙两座山,现在从甲山 处的位置向乙山 处拉电线,已知甲山 的坡比为 ,乙山 的坡比为 ,甲山上 点到河边 的距离 ,乙山上 点到河边 的距离 ,从 处看 处的俯角为 ,则河 的宽度是(参考值:,,,结果准确到 )
A. B. C. D.
如图,在菱形 中,,, 分别交 , 于点 ,,若 ,连接 .以下结论:① ;②点 到 的距离是 ;③ ;④ .其中正确的有
A. 个 B. 个 C. 个 D. 个
如图,小王在长江边某瞭望台 处,测得江面上的渔船 的俯角为 ,若 ,, 平行于江面 ,迎水坡 的坡度 ,坡长 ,则此时 的长约为(参考数据:,,).
A. B. C. D.
如图, 中,,,,点 是 边上的动点,则 的最小值为
A. B. C. D.
如图所示,菱形 的顶点 在反比例函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点.若 ,,如下结论:
① ,, 三点在同一直线上;
②点 的横坐标是 ;
③点 的坐标是 ;
④比例系数 的值为 .
其中不正确的结论是
A.①②③ B.②③④ C.①③④ D.①②④
如图, 是 的直径,弦 于点 ,点 是 上一点,且满足 ,连接 并延长交 于点 ,连接 ,,若 ,.给出下列结论:
① ;② ;③ ;④ .
其中正确的是
A.①②③ B.①②④ C.②③④ D.①②③④
如图,小明在水平面 处,测得某建筑物 的顶端 的仰角为 ,向正前方向走 米到达点 处,再往斜坡 上走 米到达点 处,测得建筑物 的顶端 的仰角为 ,已知斜坡 的坡度为 ,建筑物 垂直于平台 ,平台 与水平面 平行,点 ,,,, 均在同一平面内,则建筑物 的高度约为
(精确到 米,参考数据:,,,,,)
A. 米 B. 米 C. 米 D. 米
如图,已知 是等腰 底边上的高,且 ,边 上有一点 ,满足 则 等于
A. B. C. D.
某地下车库出口处安装了“两段式栏杆”,如图 所示,点 是栏杆转动的支点,点 是栏杆两段的联结点.当车辆经过时,栏杆 最多只能升起到如图 所示的位置,其示意图如图 所示(栏杆宽度忽略不计),其中 ,,, 米,那么适合该地下车库的车辆限高标志牌为 (参考数据:,,)
A. B. C. D.
二、填空题(共5题)
如图所示,小亮家在点 处,其所在学校的校园为矩形 ,校园东西长 米,南北长 米.学校的南门在 的中点 处, 为学校的西北角门.小亮从家到学校可以走马路:路线 (),也可以走沿河观光路:路线 .小亮在 处测得 位于北偏东 ,在 处测得 位于北偏东 ,小亮从家到学校的两条路线中,长路线比短路线多 米.(结果保留根号)
图 是邻边长为 和 的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ),则图 中所标注的 的值为 ;记图 中小正方形的中心为点 ,,,图 中的对应点为点 ,,.以大正方形的中心 为圆心作圆,则当点 ,, 在圆内或圆上时,圆的最小面积为 .
如图 ,将一个量角器与一张等边三角形()纸片放置成轴对称图形,,垂足为 ,半圆(量角器)的圆心与点 重合,此时,测得顶点 到量角器最高点的距离 ,将量角器沿 方向平移 ,半圆(量角器)恰与 的边 , 相切,如图 ,则 的长为 .
如图,这是台州市地图的一部分,分别以正东、正北方向为 轴、 轴的正方向建立直角坐标系,规定一个单位长度表示 ,甲、乙两人对着地图如下描述路桥区 处的位置
甲:路桥区 处的坐标是 ,
乙:路桥区 处在椒江区 处南偏西 方向,相距 .
则椒江区 处的坐标是 .
如图()所示的是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图()所示,两支脚 分米,展开角 ,晾衣臂 分米,晾衣臂支架 分米,且 分米.当 时,点 离地面的距离 为 分米;当 从水平状态旋转到 (在 延长线上)时,点 绕点 随之旋转至 上的点 处,则 为 分米.
三、解答题(共5题)
如图是某市一座人行天桥的示意图,天桥离地面的高 是 米,坡面 的倾斜角 ,在距 点 米处有一建筑物 .为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面 的坡度为 ,若新坡面下 处与建筑物之间需留下至少 米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据:,)
随着我市农产品整体品牌形象“聊 胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图 .线段 , 分别表示大棚的墙高和跨度, 表示保温板的长,已知墙高 为 米,墙面与保温板所成的角 ,在点 处测得 点、 点的仰角分别为 ,,如图 .求保温板 的长是多少米?(精确到 米)(参考数据:,,,,,,)
王阿姨家的阳台上放置了一个晾衣架,完全稳固张开如图().图(),()是晾衣架的侧面展开图, 是边长为 的等边三角形,晾衣架 , 能以 为圆心转动,且 ;在 , 上的点 , 处分别有支撑杆 , 能以 , 为圆心转动.
参考数据:(,,,,)
(1) 如图(),如果 经过点 ,且平行于地面 ,那么王阿姨的衣服连同衣架上的总长度是 ,垂挂在晾衣杆 上是否会拖到地面上?说明理由.
(2) 如图(),当支撑杆 支到点 ,此时 ,点 离地面距离最大.保证衣服不拖到地面上,衣服连同衣架上的总长度最长约为多少厘米?(结果取整)
如图,在 中,,作 的垂直平分线交 于点 ,延长 至点 ,使 .
(1) 若 ,求 的周长;
(2) 若 ,求 的值.
如图①, 为 上一点,点 在直径 的延长线上,且 .
(1) 判断直线 与 的位置关系,并说明理由.
(2) 若 ,,求 的半径.
(3) 如图②,在()的条件下, 的平分线 交 于点 ,交 于点 ,连接 ,求 的值.
答案
一、选择题(共20题)
1.C
2.C
3.D
4.B
5.D
6.B
7.A
8.B
9.A
10.A
11.C
12.A
13.B
14.A
15.B
16.B
17.B
18.B
19.B
20.A
二、填空题(共5题)
21.
22. ; .
23.
24.
25. ;
三、解答题(共5题)
26.要拆除.
理由:由题意得, 米, 米,
在 中,,
,
在 中,
的坡度为 ,
,
,
(米),
米 米,
该建筑物需要拆除.
27.如图所示,过点 作 于点 ,过点 作 于点 ,
则四边形 是矩形,
,,
设 ,
,,
,
则 ,,
在 中,
,,
,
则 ,.
在 中,
,
,
解得:,
即保温板 的长是 米.
28.
(1) 这个问题就是求 到地面的距离,即等边三角形 的高,并与 比较.
等边三角形 的边长为 ,
它的高为 ,正好要拖到地面.
(2) 过点 作 ,垂足为点 .
由题意,得 ,,
.点 到地面 的距离为 .
答:保证衣服不拖到地面上,衣服连同衣架上的总长度最长约为 厘米.
29.
(1) 设 的垂直平分线交 于点 ,连接 .
是 的垂直平分线,
.
.
,,
.
(2) 设 ,则 ,
由(),得 ,
,
在 中,,
.
30.
(1) 与 相切.
理由:连接 .
,
.
,
.
为 的直径,
.
.
,
即 .
为 的半径,
与 相切.
(2) 由()知,.
,
,
在 中,,
,,
.
.
.
.
.
.
(3) 如图,连接 ,过点 作 于点 .
平分 ,
.
.
在 中,.
在 中,,,
,.
,,
,
.
设 ,则 ,.
在 中,由勾股定理,得 ,
,
即 ,
解得 ,(不合题意,舍去).
,
在 中,.
一、选择题(共20题)
数学活动课上,小敏、小颖分别画了 和 ,尺寸如图.如果两个三角形的面积分别记作 ,,那么它们的大小关系是
A. B. C. D.不能确定
如图, 中,,, 所对的三边分别记为 ,,, 是 的外心,,,,则 等于
A. B.
C. D.
如图,一电线杆 的高为 米,当太阳光线与地面的夹角为 时,其影长 约为 ( 取 ,结果精确到 米)
A. 米 B. 米 C. 米 D. 米
如图,矩形 中, 为 的中点,,,连接 并延长,交 的延长线于点 ,, 相交于点 .下列结论:
① 平分 ;
② ;
③ ;
④ .
其中正确的是
A.①②③ B.①②④ C.①③④ D.③④
如图,已知点 是第一象限内横坐标为 的一个定点, 于点 ,交直线 于点 ,若点 是线段 上的一个动点,,,点 在线段 上运动时, 点不变, 点随之运动,当点 从点 运动到点 时,则点 运动的路径长是
A. B. C. D.
如图,在距某居民楼 楼底 点左侧水平距离 的 点处有一个山坡,山坡 的坡度(或坡比),山坡坡底 点到坡顶 点的距离 ,在坡顶 点处测得居民楼楼顶 点的仰角为 ,居民楼 与山坡 的剖面在同一平面内,则居民楼 的高度约为(参考数据:,,)
A. B. C. D.
某游乐场一滑梯的竖直高度为 ,滑梯的坡角为 ,那么滑梯长为
A. B. C. D.
在 中,,,,则下列结论中,正确的是
A. B. C. D.
王师傅在楼顶上的点 处测得楼前一棵树 的顶端 的俯角为 , 又知水平距离 ,楼高 ,则树高 为
A. B.
C. D.
如图,在等腰 中,,, 是 上一点,若 ,则 的长为
A. B. C. D.
如图,为一副重叠放置的三角板,其中 , 与 共线,将 沿 方向平移,当 经过 的中点 时,直线 交 于点 ,若 ,则此时 的长度为
A. B. C. D.
如图,在河流两边有甲、乙两座山,现在从甲山 处的位置向乙山 处拉电线,已知甲山 的坡比为 ,乙山 的坡比为 ,甲山上 点到河边 的距离 ,乙山上 点到河边 的距离 ,从 处看 处的俯角为 ,则河 的宽度是(参考值:,,,结果准确到 )
A. B. C. D.
如图,在菱形 中,,, 分别交 , 于点 ,,若 ,连接 .以下结论:① ;②点 到 的距离是 ;③ ;④ .其中正确的有
A. 个 B. 个 C. 个 D. 个
如图,小王在长江边某瞭望台 处,测得江面上的渔船 的俯角为 ,若 ,, 平行于江面 ,迎水坡 的坡度 ,坡长 ,则此时 的长约为(参考数据:,,).
A. B. C. D.
如图, 中,,,,点 是 边上的动点,则 的最小值为
A. B. C. D.
如图所示,菱形 的顶点 在反比例函数 的图象上,函数 的图象关于直线 对称,且经过点 , 两点.若 ,,如下结论:
① ,, 三点在同一直线上;
②点 的横坐标是 ;
③点 的坐标是 ;
④比例系数 的值为 .
其中不正确的结论是
A.①②③ B.②③④ C.①③④ D.①②④
如图, 是 的直径,弦 于点 ,点 是 上一点,且满足 ,连接 并延长交 于点 ,连接 ,,若 ,.给出下列结论:
① ;② ;③ ;④ .
其中正确的是
A.①②③ B.①②④ C.②③④ D.①②③④
如图,小明在水平面 处,测得某建筑物 的顶端 的仰角为 ,向正前方向走 米到达点 处,再往斜坡 上走 米到达点 处,测得建筑物 的顶端 的仰角为 ,已知斜坡 的坡度为 ,建筑物 垂直于平台 ,平台 与水平面 平行,点 ,,,, 均在同一平面内,则建筑物 的高度约为
(精确到 米,参考数据:,,,,,)
A. 米 B. 米 C. 米 D. 米
如图,已知 是等腰 底边上的高,且 ,边 上有一点 ,满足 则 等于
A. B. C. D.
某地下车库出口处安装了“两段式栏杆”,如图 所示,点 是栏杆转动的支点,点 是栏杆两段的联结点.当车辆经过时,栏杆 最多只能升起到如图 所示的位置,其示意图如图 所示(栏杆宽度忽略不计),其中 ,,, 米,那么适合该地下车库的车辆限高标志牌为 (参考数据:,,)
A. B. C. D.
二、填空题(共5题)
如图所示,小亮家在点 处,其所在学校的校园为矩形 ,校园东西长 米,南北长 米.学校的南门在 的中点 处, 为学校的西北角门.小亮从家到学校可以走马路:路线 (),也可以走沿河观光路:路线 .小亮在 处测得 位于北偏东 ,在 处测得 位于北偏东 ,小亮从家到学校的两条路线中,长路线比短路线多 米.(结果保留根号)
图 是邻边长为 和 的矩形,它由三个小正方形组成,将其剪拼成不重叠、无缝隙的大正方形(如图 ),则图 中所标注的 的值为 ;记图 中小正方形的中心为点 ,,,图 中的对应点为点 ,,.以大正方形的中心 为圆心作圆,则当点 ,, 在圆内或圆上时,圆的最小面积为 .
如图 ,将一个量角器与一张等边三角形()纸片放置成轴对称图形,,垂足为 ,半圆(量角器)的圆心与点 重合,此时,测得顶点 到量角器最高点的距离 ,将量角器沿 方向平移 ,半圆(量角器)恰与 的边 , 相切,如图 ,则 的长为 .
如图,这是台州市地图的一部分,分别以正东、正北方向为 轴、 轴的正方向建立直角坐标系,规定一个单位长度表示 ,甲、乙两人对着地图如下描述路桥区 处的位置
甲:路桥区 处的坐标是 ,
乙:路桥区 处在椒江区 处南偏西 方向,相距 .
则椒江区 处的坐标是 .
如图()所示的是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图()所示,两支脚 分米,展开角 ,晾衣臂 分米,晾衣臂支架 分米,且 分米.当 时,点 离地面的距离 为 分米;当 从水平状态旋转到 (在 延长线上)时,点 绕点 随之旋转至 上的点 处,则 为 分米.
三、解答题(共5题)
如图是某市一座人行天桥的示意图,天桥离地面的高 是 米,坡面 的倾斜角 ,在距 点 米处有一建筑物 .为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面 的坡度为 ,若新坡面下 处与建筑物之间需留下至少 米宽的人行道,问该建筑物是否需要拆除?(计算最后结果保留一位小数).(参考数据:,)
随着我市农产品整体品牌形象“聊 胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图 .线段 , 分别表示大棚的墙高和跨度, 表示保温板的长,已知墙高 为 米,墙面与保温板所成的角 ,在点 处测得 点、 点的仰角分别为 ,,如图 .求保温板 的长是多少米?(精确到 米)(参考数据:,,,,,,)
王阿姨家的阳台上放置了一个晾衣架,完全稳固张开如图().图(),()是晾衣架的侧面展开图, 是边长为 的等边三角形,晾衣架 , 能以 为圆心转动,且 ;在 , 上的点 , 处分别有支撑杆 , 能以 , 为圆心转动.
参考数据:(,,,,)
(1) 如图(),如果 经过点 ,且平行于地面 ,那么王阿姨的衣服连同衣架上的总长度是 ,垂挂在晾衣杆 上是否会拖到地面上?说明理由.
(2) 如图(),当支撑杆 支到点 ,此时 ,点 离地面距离最大.保证衣服不拖到地面上,衣服连同衣架上的总长度最长约为多少厘米?(结果取整)
如图,在 中,,作 的垂直平分线交 于点 ,延长 至点 ,使 .
(1) 若 ,求 的周长;
(2) 若 ,求 的值.
如图①, 为 上一点,点 在直径 的延长线上,且 .
(1) 判断直线 与 的位置关系,并说明理由.
(2) 若 ,,求 的半径.
(3) 如图②,在()的条件下, 的平分线 交 于点 ,交 于点 ,连接 ,求 的值.
答案
一、选择题(共20题)
1.C
2.C
3.D
4.B
5.D
6.B
7.A
8.B
9.A
10.A
11.C
12.A
13.B
14.A
15.B
16.B
17.B
18.B
19.B
20.A
二、填空题(共5题)
21.
22. ; .
23.
24.
25. ;
三、解答题(共5题)
26.要拆除.
理由:由题意得, 米, 米,
在 中,,
,
在 中,
的坡度为 ,
,
,
(米),
米 米,
该建筑物需要拆除.
27.如图所示,过点 作 于点 ,过点 作 于点 ,
则四边形 是矩形,
,,
设 ,
,,
,
则 ,,
在 中,
,,
,
则 ,.
在 中,
,
,
解得:,
即保温板 的长是 米.
28.
(1) 这个问题就是求 到地面的距离,即等边三角形 的高,并与 比较.
等边三角形 的边长为 ,
它的高为 ,正好要拖到地面.
(2) 过点 作 ,垂足为点 .
由题意,得 ,,
.点 到地面 的距离为 .
答:保证衣服不拖到地面上,衣服连同衣架上的总长度最长约为 厘米.
29.
(1) 设 的垂直平分线交 于点 ,连接 .
是 的垂直平分线,
.
.
,,
.
(2) 设 ,则 ,
由(),得 ,
,
在 中,,
.
30.
(1) 与 相切.
理由:连接 .
,
.
,
.
为 的直径,
.
.
,
即 .
为 的半径,
与 相切.
(2) 由()知,.
,
,
在 中,,
,,
.
.
.
.
.
.
(3) 如图,连接 ,过点 作 于点 .
平分 ,
.
.
在 中,.
在 中,,,
,.
,,
,
.
设 ,则 ,.
在 中,由勾股定理,得 ,
,
即 ,
解得 ,(不合题意,舍去).
,
在 中,.
