2021-2022学年青岛版七年级上学期数学期末练习试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版七年级上学期数学期末练习试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 19:32:50 | ||
图片预览




文档简介
2021-2022学年青岛新版七年级上学期数学期末练习试卷
一.选择题(共12小题,满分36分,每小题3分)
1.下列对代数式a﹣的描述,正确的是( )
A.a与b的相反数的差
B.a与b的差的倒数
C.a与b的倒数的差
D.a的相反数与b的差的倒数
2.如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“善”字相对的面上的字是( )
A.文 B.明 C.诚 D.信
3.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
4.若关于x的方程1+ax=3的解是x=﹣2,则a的值是( )
A.﹣2 B.﹣1 C.21 D.2
5.有理数a、b在数轴上分别对应的点为M、N,则下列式子结果为负数的个数是( )
①a+b;②a﹣b;③﹣a+b;④﹣a﹣b;⑤ab;⑥;⑦a3b3;⑧b3﹣a3
A.4个 B.5个 C.6个 D.7个
6.根据世界卫生组织的统计,截止10月28日,全球新冠确诊病例累计超过4430万,用科学记数法表示这一数据是( )
A.4.43×107 B.0.443×108 C.44.3×106 D.4.43×108
7.在解方程时,去分母正确的是( )
A.3(x﹣1)﹣2(2+3x)=1 B.3(x﹣1)+2(2x+3)=1
C.3(x﹣1)+2(2+3x)=6 D.3(x﹣1)﹣2(2x+3)=6
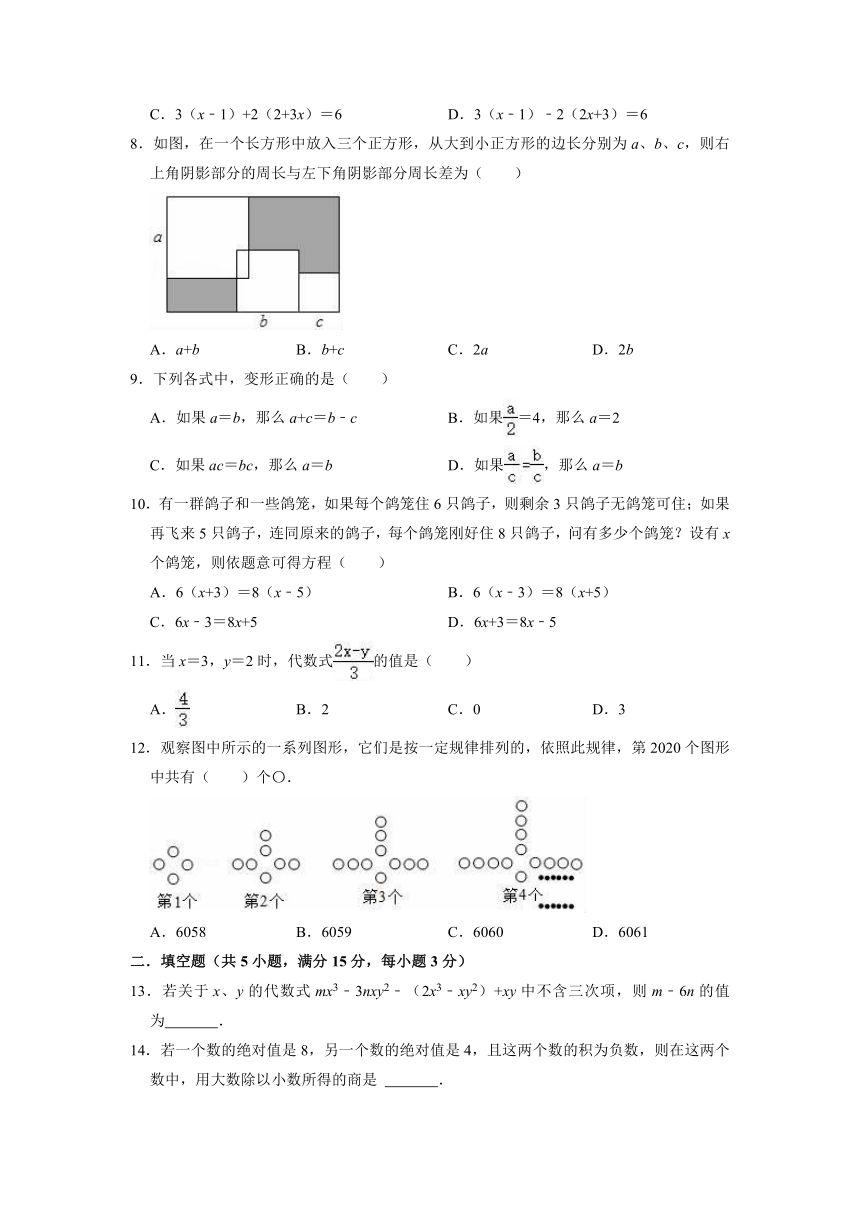
8.如图,在一个长方形中放入三个正方形,从大到小正方形的边长分别为a、b、c,则右上角阴影部分的周长与左下角阴影部分周长差为( )
A.a+b B.b+c C.2a D.2b
9.下列各式中,变形正确的是( )
A.如果a=b,那么a+c=b﹣c B.如果=4,那么a=2
C.如果ac=bc,那么a=b D.如果,那么a=b
10.有一群鸽子和一些鸽笼,如果每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子,问有多少个鸽笼?设有x个鸽笼,则依题意可得方程( )
A.6(x+3)=8(x﹣5) B.6(x﹣3)=8(x+5)
C.6x﹣3=8x+5 D.6x+3=8x﹣5
11.当x=3,y=2时,代数式的值是( )
A. B.2 C.0 D.3
12.观察图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2020个图形中共有( )个〇.
A.6058 B.6059 C.6060 D.6061
二.填空题(共5小题,满分15分,每小题3分)
13.若关于x、y的代数式mx3﹣3nxy2﹣(2x3﹣xy2)+xy中不含三次项,则m﹣6n的值为 .
14.若一个数的绝对值是8,另一个数的绝对值是4,且这两个数的积为负数,则在这两个数中,用大数除以小数所得的商是 .
15.如图所示,直径为1个单位长度的圆从原点沿着数轴负半轴方向无滑动的滚动一周到达A点,则A点表示的数是 .
16.已知关于x的方程3x﹣2k=2的解是x=k﹣2,则k的值是 .
17.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}==,min{﹣1,2,3}=﹣1,如果M{3,2x+1,4x﹣1}=min{2.2,﹣x+3,5x},那么x= .
三.解答题(共8小题,满分69分)
18.(8分)计算:
(1)|3﹣5|﹣(5﹣23);
(2)﹣32+|2﹣3|﹣(﹣2)2.
19.(8分)解方程:
(1)2(x﹣1)=2﹣5(x+2);
(2).
20.(8分)先化简,再求值:(4a2b﹣3ab2)﹣(﹣a2b+2ab2),其中a=1,b=2.
21.(7分)2018年,小明家第一季度用电量是650千瓦时,已知第一季度用电量比第四季度用电量多30%.如图是依据各个季度用电量所占全年用电量的百分比而绘制的扇形图,根据图形提供的信息,回答下列问题:
(1)求第四季度的用电量.
(2)如果第二季度用电量是第三季度用电量的,则第三季度用电量在扇形图中的圆心角是 度.
(3)随着科技和生活水平的提高,家里的用电器越来越多,小明家预计2019年用电总量比2018年增长8%,而2020年的增长率在上一年的基础上提高2个百分点,那么估计小明家在2020年的用电量是多少千瓦时?
22.(8分)一次数学测验后,王老师把某一小组10名同学的成绩以平均成绩为基准,并以高于平均成绩记为“+”,分别记为+10分,﹣5分,0分,+8分,﹣3分,+6分,﹣5分,﹣3分,+4分,﹣12分,通过计算知道这10名同学的平均成绩是82分.
(1)这一小组成绩最高分与最低分相差多少分?
(2)如果成绩不低于80分为优秀,那么这10名同学在这次数学测验中优秀率是百分之几?
23.(8分)一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
24.(10分)如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
(1)当t=2时,①AB= cm,②此时线段CD的长度= cm;
(2)用含有t的代数式表示运动过程中AB的长;
(3)在运动过程中,若AB中点为E,则EC的长度是否变化?若不变,求出EC的长;若变化,请说明理由.
25.(12分)如图1,点C把线段AB分成两条线段AC和BC,如果AC=2BC时,则称点C是线段AB的内二倍分割点;
如图2,如果BC=2AC时,则称点C是线段BA的内二倍分割点.
例如:如图3,数轴上,点A、B、C、D分别表示数﹣1、2、1、0,则点C是线段AB的内二倍分割点;点D是线段BA内二倍分割点.
(1)如图4,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为7.MN的内二倍分割点表示的数是 ;NM的内二倍分割点表示的数是 .
(2)如图5,数轴上,点A所表示的数为﹣30,点B所表示的数为20.点P从点B出发,以2个单位每秒的速度沿
数轴向左运动,设运动时间为t(t>0)秒.
①线段BP的长为 ;(用含t的式子表示)
②求当t为何值时,P、A、B三个点中恰有一个点为其余两点的内二倍分割点.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:用数学语言叙述代数式a﹣为a与b的倒数的差,
故选:C.
2.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
在正方体盒子上与“善”字相对的面上的字是“文”.
故选:A.
3.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
4.解:把x=﹣2代入方程,得1﹣2a=3,
解得a=﹣1.
故选:B.
5.解:由点M、N在数轴上的位置可得,a<0,b>0,且|a|>|b|,
因此,①a+b<0,是负数;②a﹣b<0,是负数;③﹣a+b>0,是正数;④﹣a﹣b>0,是正数;⑤ab<0,是负数;⑥<0,是负数;⑦a3b3<0,是负数;⑧b3﹣a3>0,是正数,
则结果为负数的个数是5个.
故选:B.
6.解:4430万=44300000=4.43×107.
故选:A.
7.解:两边都乘以6得,3(x﹣1)﹣2(2x+3)=6.
故选:D.
8.解:设重叠部分的小长方形的长与宽分别为x和y,
∴阴影部分的周长为:
2(a+b﹣x﹣c)+2(b+c﹣y)﹣2(b﹣x)﹣2(a﹣y)
=2a+2b﹣2x﹣2c+2b+2c﹣2y﹣2b+2x﹣2a+2y
=2b.
故选:D.
9.解:A、若c≠0时,等式a+c=b﹣c不成立,故本选项不符合题意.
B、如果=4,那么a=8,故本选项不符合题意.
C、若c=0时,等式a=b不成立,故本选项不符合题意.
D、如果,那么a=b,故本选项符合题意.
故选:D.
10.解:有x个鸽笼,
根据题意每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子知:6x+3=8x﹣5,
故选:D.
11.解:==
12.解:观察图形的变化可知:
第1个图形中共有3×1+1=4个〇;
第2个图形中共有3×2+1=7个〇;
第3个图形中共有3×3+1=10个〇;
…
所以第n个图形中共有(3n+1)个〇;
所以第2020个图形中共有〇的个数为:3×2020+1=6061.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
13.解:mx3﹣3nxy2﹣(2x3﹣xy2)+xy=(m﹣2)x3+(1﹣3n)xy2+xy,
∵关于x、y的代数式mx3﹣3nxy2﹣(2x3﹣xy2)+xy中不含三次项,
∴m﹣2=0,1﹣3n=0,
解得m=2,n=,
∴m﹣6n=2﹣=2﹣2=0.
故答案为:0.
14.解:根据题意可得,
|a|=8,|b|=4,
解得a=±8,b=±4,
若两数积为负数,则8×(﹣4)=﹣32,﹣8×(4)=﹣32,
所以用大数除以小数所得的商为:或.
故答案为:﹣2或﹣.
15.解:∵直径为单位1的圆的周长=2π =π,
∴OA=π,
∴点A表示的数为﹣π.
故答案为:﹣π.
16.解:把x=k﹣2代入方程得:3(k﹣2)﹣2k=2,
去括号得:3k﹣6﹣2k=2,
解得:k=8,
故答案为:8
17.解:M{3,2x+1,4x﹣1}=min{2.2,﹣x+3,5x},
①若(3+2x+1+4x﹣1)=2.2,则x=,(符合题意)
②若(3+2x+1+4x﹣1)=﹣x+3,则x=,(﹣x+3不是三个数中最小的数,不符合题意)
③若(3+2x+1+4x﹣1)=5x,则x=,(符合题意)
故答案为:或.
三.解答题(共8小题,满分69分)
18.解:(1)|3﹣5|﹣(5﹣23)
=|﹣2|﹣(﹣18)
=2+18
=20;
(2)﹣32+|2﹣3|﹣(﹣2)2
=﹣9+|﹣1|﹣4
=﹣9+1﹣4
=﹣12.
19.解:(1)去括号得:2x﹣2=2﹣5x﹣10,
移项得:2x+5x=2﹣10+2,
合并得:7x=﹣6,
解得:x=﹣;
(2)去分母得:2(5x+1)﹣(7x+2)=4,
去括号得:10x+2﹣7x﹣2=4,
移项得:10x﹣7x=4﹣2+2,
合并得:3x=4,
解得:x=.
20.解:(4a2b﹣3ab2)﹣(﹣a2b+2ab2)
=4a2b﹣3ab2+a2b﹣2ab2
=5a2b﹣5ab2,
当a=1,b=2时,
原式=5×12×2﹣5×1×22=10﹣20=﹣10.
21.解:(1)设第四季度的用电量为x千瓦时,
根据题意(1+30%)x=650,
解得x=500.
第四季度的用电量为500千瓦时;
(2)第四季度用电量500千瓦时占20%,
全年用电量为:=2500千瓦时,
第二、第三季度的用电量共为:2500﹣500﹣650=1350千瓦时,
如果第二季度用电量是第三季度用电量的,则第二季度用电量为450千瓦时,第三季度为900千瓦时,
第三季度用电量在扇形图中的圆心角度数为:360×=129.6°,
故答案为129.6.
(3)估计小明家在2020年的用电量为2500(1+8%)(1+10%)=2970千瓦时.
22.解:(1)+10﹣(﹣12)=22(分).
答:这一小组成绩最高分与最低分相差22分;
(2)5÷10×100%=50%.
故这10名同学在这次数学测验中优秀率是50%.
23.解:(1)设无风时飞机的速度为x千米每小时,两城之间的距离为S千米.
则顺风飞行时的速度v1=x+24,逆风飞行的速度v2=x﹣24
顺风飞行时:S=v1t1
逆风飞行时:S=v2t2
即S=(x+24)×=(x﹣24)×3
解得x=840,
答:无风时飞机的飞行速度为840千米每小时.
(2)两城之间的距离S=(x﹣24)×3=2448千米
答:两城之间的距离为2448千米.
24.解:(1)当t=2时,①AB=2×2=4cm,
故答案为:4;
②BD=AD﹣AB=10﹣4=6cm,
由C是线段BD的中点,得
CD=BD=×6=3cm,
故答案为:3.
(2)点B沿点A→D运动时,AB=2tcm,
点B沿点D→A运动时,AB=20﹣2tcm;
(3)在运动过程中,若AB中点为E,则EC的长不变,
由AB中点为E,C是线段BD的中点,得
BE=AB,BC=BD.
EC=BE+BC=(AB+BD)=×10=5cm.
25.解:(1)∵M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为7,
∴MN=7﹣(﹣2)=9,
∴MN的内二倍分割点表示的数是:﹣2+MN=﹣2+×9=4;
NM的内二倍分割点表示的数是:﹣2+MN=﹣2+×9=1.
故答案为:4;1;
(2)①依题意可得,线段BP的长为2t.
故答案为:2t;
②当P在线段AB上时,P为线段AB的内二倍分割点,有以下两种情况:
如果P是AB的内二倍分割点时,则AP=2BP,
所以50﹣2t=2×2t,
解得t=;
如果P是BA的内二倍分割点时,则BP=2AP,
所以2t=2(50﹣2t),
解得t=;
当P在点A左侧时,A为线段PB的内二倍分割点,有以下两种情况:
如果A是BP的内二倍分割点时,则BA=2PA,
所以50=2(2t﹣50),
解得t=;
如果A是PB的内二倍分割点时,则PA=2BA,
所以2t﹣50=2×50,
解得t=75;
综上所述:当t为,,,75时,P、A、B中恰有一个点为其余两点的内二倍分割点.
一.选择题(共12小题,满分36分,每小题3分)
1.下列对代数式a﹣的描述,正确的是( )
A.a与b的相反数的差
B.a与b的差的倒数
C.a与b的倒数的差
D.a的相反数与b的差的倒数
2.如图,是小明同学在数学实践课上,所设计的正方体盒子的平面展开图,每个面上都有一个汉字,请你判断,正方体盒子上与“善”字相对的面上的字是( )
A.文 B.明 C.诚 D.信
3.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
4.若关于x的方程1+ax=3的解是x=﹣2,则a的值是( )
A.﹣2 B.﹣1 C.21 D.2
5.有理数a、b在数轴上分别对应的点为M、N,则下列式子结果为负数的个数是( )
①a+b;②a﹣b;③﹣a+b;④﹣a﹣b;⑤ab;⑥;⑦a3b3;⑧b3﹣a3
A.4个 B.5个 C.6个 D.7个
6.根据世界卫生组织的统计,截止10月28日,全球新冠确诊病例累计超过4430万,用科学记数法表示这一数据是( )
A.4.43×107 B.0.443×108 C.44.3×106 D.4.43×108
7.在解方程时,去分母正确的是( )
A.3(x﹣1)﹣2(2+3x)=1 B.3(x﹣1)+2(2x+3)=1
C.3(x﹣1)+2(2+3x)=6 D.3(x﹣1)﹣2(2x+3)=6
8.如图,在一个长方形中放入三个正方形,从大到小正方形的边长分别为a、b、c,则右上角阴影部分的周长与左下角阴影部分周长差为( )
A.a+b B.b+c C.2a D.2b
9.下列各式中,变形正确的是( )
A.如果a=b,那么a+c=b﹣c B.如果=4,那么a=2
C.如果ac=bc,那么a=b D.如果,那么a=b
10.有一群鸽子和一些鸽笼,如果每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子,问有多少个鸽笼?设有x个鸽笼,则依题意可得方程( )
A.6(x+3)=8(x﹣5) B.6(x﹣3)=8(x+5)
C.6x﹣3=8x+5 D.6x+3=8x﹣5
11.当x=3,y=2时,代数式的值是( )
A. B.2 C.0 D.3
12.观察图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2020个图形中共有( )个〇.
A.6058 B.6059 C.6060 D.6061
二.填空题(共5小题,满分15分,每小题3分)
13.若关于x、y的代数式mx3﹣3nxy2﹣(2x3﹣xy2)+xy中不含三次项,则m﹣6n的值为 .
14.若一个数的绝对值是8,另一个数的绝对值是4,且这两个数的积为负数,则在这两个数中,用大数除以小数所得的商是 .
15.如图所示,直径为1个单位长度的圆从原点沿着数轴负半轴方向无滑动的滚动一周到达A点,则A点表示的数是 .
16.已知关于x的方程3x﹣2k=2的解是x=k﹣2,则k的值是 .
17.对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{﹣1,2,3}==,min{﹣1,2,3}=﹣1,如果M{3,2x+1,4x﹣1}=min{2.2,﹣x+3,5x},那么x= .
三.解答题(共8小题,满分69分)
18.(8分)计算:
(1)|3﹣5|﹣(5﹣23);
(2)﹣32+|2﹣3|﹣(﹣2)2.
19.(8分)解方程:
(1)2(x﹣1)=2﹣5(x+2);
(2).
20.(8分)先化简,再求值:(4a2b﹣3ab2)﹣(﹣a2b+2ab2),其中a=1,b=2.
21.(7分)2018年,小明家第一季度用电量是650千瓦时,已知第一季度用电量比第四季度用电量多30%.如图是依据各个季度用电量所占全年用电量的百分比而绘制的扇形图,根据图形提供的信息,回答下列问题:
(1)求第四季度的用电量.
(2)如果第二季度用电量是第三季度用电量的,则第三季度用电量在扇形图中的圆心角是 度.
(3)随着科技和生活水平的提高,家里的用电器越来越多,小明家预计2019年用电总量比2018年增长8%,而2020年的增长率在上一年的基础上提高2个百分点,那么估计小明家在2020年的用电量是多少千瓦时?
22.(8分)一次数学测验后,王老师把某一小组10名同学的成绩以平均成绩为基准,并以高于平均成绩记为“+”,分别记为+10分,﹣5分,0分,+8分,﹣3分,+6分,﹣5分,﹣3分,+4分,﹣12分,通过计算知道这10名同学的平均成绩是82分.
(1)这一小组成绩最高分与最低分相差多少分?
(2)如果成绩不低于80分为优秀,那么这10名同学在这次数学测验中优秀率是百分之几?
23.(8分)一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.
(1)求无风时飞机的飞行速度;
(2)求两城之间的距离.
24.(10分)如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
(1)当t=2时,①AB= cm,②此时线段CD的长度= cm;
(2)用含有t的代数式表示运动过程中AB的长;
(3)在运动过程中,若AB中点为E,则EC的长度是否变化?若不变,求出EC的长;若变化,请说明理由.
25.(12分)如图1,点C把线段AB分成两条线段AC和BC,如果AC=2BC时,则称点C是线段AB的内二倍分割点;
如图2,如果BC=2AC时,则称点C是线段BA的内二倍分割点.
例如:如图3,数轴上,点A、B、C、D分别表示数﹣1、2、1、0,则点C是线段AB的内二倍分割点;点D是线段BA内二倍分割点.
(1)如图4,M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为7.MN的内二倍分割点表示的数是 ;NM的内二倍分割点表示的数是 .
(2)如图5,数轴上,点A所表示的数为﹣30,点B所表示的数为20.点P从点B出发,以2个单位每秒的速度沿
数轴向左运动,设运动时间为t(t>0)秒.
①线段BP的长为 ;(用含t的式子表示)
②求当t为何值时,P、A、B三个点中恰有一个点为其余两点的内二倍分割点.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:用数学语言叙述代数式a﹣为a与b的倒数的差,
故选:C.
2.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
在正方体盒子上与“善”字相对的面上的字是“文”.
故选:A.
3.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
4.解:把x=﹣2代入方程,得1﹣2a=3,
解得a=﹣1.
故选:B.
5.解:由点M、N在数轴上的位置可得,a<0,b>0,且|a|>|b|,
因此,①a+b<0,是负数;②a﹣b<0,是负数;③﹣a+b>0,是正数;④﹣a﹣b>0,是正数;⑤ab<0,是负数;⑥<0,是负数;⑦a3b3<0,是负数;⑧b3﹣a3>0,是正数,
则结果为负数的个数是5个.
故选:B.
6.解:4430万=44300000=4.43×107.
故选:A.
7.解:两边都乘以6得,3(x﹣1)﹣2(2x+3)=6.
故选:D.
8.解:设重叠部分的小长方形的长与宽分别为x和y,
∴阴影部分的周长为:
2(a+b﹣x﹣c)+2(b+c﹣y)﹣2(b﹣x)﹣2(a﹣y)
=2a+2b﹣2x﹣2c+2b+2c﹣2y﹣2b+2x﹣2a+2y
=2b.
故选:D.
9.解:A、若c≠0时,等式a+c=b﹣c不成立,故本选项不符合题意.
B、如果=4,那么a=8,故本选项不符合题意.
C、若c=0时,等式a=b不成立,故本选项不符合题意.
D、如果,那么a=b,故本选项符合题意.
故选:D.
10.解:有x个鸽笼,
根据题意每个鸽笼住6只鸽子,则剩余3只鸽子无鸽笼可住;如果再飞来5只鸽子,连同原来的鸽子,每个鸽笼刚好住8只鸽子知:6x+3=8x﹣5,
故选:D.
11.解:==
12.解:观察图形的变化可知:
第1个图形中共有3×1+1=4个〇;
第2个图形中共有3×2+1=7个〇;
第3个图形中共有3×3+1=10个〇;
…
所以第n个图形中共有(3n+1)个〇;
所以第2020个图形中共有〇的个数为:3×2020+1=6061.
故选:D.
二.填空题(共5小题,满分15分,每小题3分)
13.解:mx3﹣3nxy2﹣(2x3﹣xy2)+xy=(m﹣2)x3+(1﹣3n)xy2+xy,
∵关于x、y的代数式mx3﹣3nxy2﹣(2x3﹣xy2)+xy中不含三次项,
∴m﹣2=0,1﹣3n=0,
解得m=2,n=,
∴m﹣6n=2﹣=2﹣2=0.
故答案为:0.
14.解:根据题意可得,
|a|=8,|b|=4,
解得a=±8,b=±4,
若两数积为负数,则8×(﹣4)=﹣32,﹣8×(4)=﹣32,
所以用大数除以小数所得的商为:或.
故答案为:﹣2或﹣.
15.解:∵直径为单位1的圆的周长=2π =π,
∴OA=π,
∴点A表示的数为﹣π.
故答案为:﹣π.
16.解:把x=k﹣2代入方程得:3(k﹣2)﹣2k=2,
去括号得:3k﹣6﹣2k=2,
解得:k=8,
故答案为:8
17.解:M{3,2x+1,4x﹣1}=min{2.2,﹣x+3,5x},
①若(3+2x+1+4x﹣1)=2.2,则x=,(符合题意)
②若(3+2x+1+4x﹣1)=﹣x+3,则x=,(﹣x+3不是三个数中最小的数,不符合题意)
③若(3+2x+1+4x﹣1)=5x,则x=,(符合题意)
故答案为:或.
三.解答题(共8小题,满分69分)
18.解:(1)|3﹣5|﹣(5﹣23)
=|﹣2|﹣(﹣18)
=2+18
=20;
(2)﹣32+|2﹣3|﹣(﹣2)2
=﹣9+|﹣1|﹣4
=﹣9+1﹣4
=﹣12.
19.解:(1)去括号得:2x﹣2=2﹣5x﹣10,
移项得:2x+5x=2﹣10+2,
合并得:7x=﹣6,
解得:x=﹣;
(2)去分母得:2(5x+1)﹣(7x+2)=4,
去括号得:10x+2﹣7x﹣2=4,
移项得:10x﹣7x=4﹣2+2,
合并得:3x=4,
解得:x=.
20.解:(4a2b﹣3ab2)﹣(﹣a2b+2ab2)
=4a2b﹣3ab2+a2b﹣2ab2
=5a2b﹣5ab2,
当a=1,b=2时,
原式=5×12×2﹣5×1×22=10﹣20=﹣10.
21.解:(1)设第四季度的用电量为x千瓦时,
根据题意(1+30%)x=650,
解得x=500.
第四季度的用电量为500千瓦时;
(2)第四季度用电量500千瓦时占20%,
全年用电量为:=2500千瓦时,
第二、第三季度的用电量共为:2500﹣500﹣650=1350千瓦时,
如果第二季度用电量是第三季度用电量的,则第二季度用电量为450千瓦时,第三季度为900千瓦时,
第三季度用电量在扇形图中的圆心角度数为:360×=129.6°,
故答案为129.6.
(3)估计小明家在2020年的用电量为2500(1+8%)(1+10%)=2970千瓦时.
22.解:(1)+10﹣(﹣12)=22(分).
答:这一小组成绩最高分与最低分相差22分;
(2)5÷10×100%=50%.
故这10名同学在这次数学测验中优秀率是50%.
23.解:(1)设无风时飞机的速度为x千米每小时,两城之间的距离为S千米.
则顺风飞行时的速度v1=x+24,逆风飞行的速度v2=x﹣24
顺风飞行时:S=v1t1
逆风飞行时:S=v2t2
即S=(x+24)×=(x﹣24)×3
解得x=840,
答:无风时飞机的飞行速度为840千米每小时.
(2)两城之间的距离S=(x﹣24)×3=2448千米
答:两城之间的距离为2448千米.
24.解:(1)当t=2时,①AB=2×2=4cm,
故答案为:4;
②BD=AD﹣AB=10﹣4=6cm,
由C是线段BD的中点,得
CD=BD=×6=3cm,
故答案为:3.
(2)点B沿点A→D运动时,AB=2tcm,
点B沿点D→A运动时,AB=20﹣2tcm;
(3)在运动过程中,若AB中点为E,则EC的长不变,
由AB中点为E,C是线段BD的中点,得
BE=AB,BC=BD.
EC=BE+BC=(AB+BD)=×10=5cm.
25.解:(1)∵M、N为数轴上两点,点M所表示的数为﹣2,点N所表示的数为7,
∴MN=7﹣(﹣2)=9,
∴MN的内二倍分割点表示的数是:﹣2+MN=﹣2+×9=4;
NM的内二倍分割点表示的数是:﹣2+MN=﹣2+×9=1.
故答案为:4;1;
(2)①依题意可得,线段BP的长为2t.
故答案为:2t;
②当P在线段AB上时,P为线段AB的内二倍分割点,有以下两种情况:
如果P是AB的内二倍分割点时,则AP=2BP,
所以50﹣2t=2×2t,
解得t=;
如果P是BA的内二倍分割点时,则BP=2AP,
所以2t=2(50﹣2t),
解得t=;
当P在点A左侧时,A为线段PB的内二倍分割点,有以下两种情况:
如果A是BP的内二倍分割点时,则BA=2PA,
所以50=2(2t﹣50),
解得t=;
如果A是PB的内二倍分割点时,则PA=2BA,
所以2t﹣50=2×50,
解得t=75;
综上所述:当t为,,,75时,P、A、B中恰有一个点为其余两点的内二倍分割点.
同课章节目录
