2021-2022学年北师大版七年级数学上册专题05 期末复习专题训练 6.3 数据的表示 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册专题05 期末复习专题训练 6.3 数据的表示 (Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览



文档简介
专题05 : 2021年北师大新版七年级(上) 6.3 数据的表示 - 期末复习专题训练
一、选择题(共10小题)
1.某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
2.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图所示,该调查的方式是( ),图中的a的值是( )
A.全面调查,26 B.全面调查,24
C.抽样调查,26 D.抽样调查,24
3.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
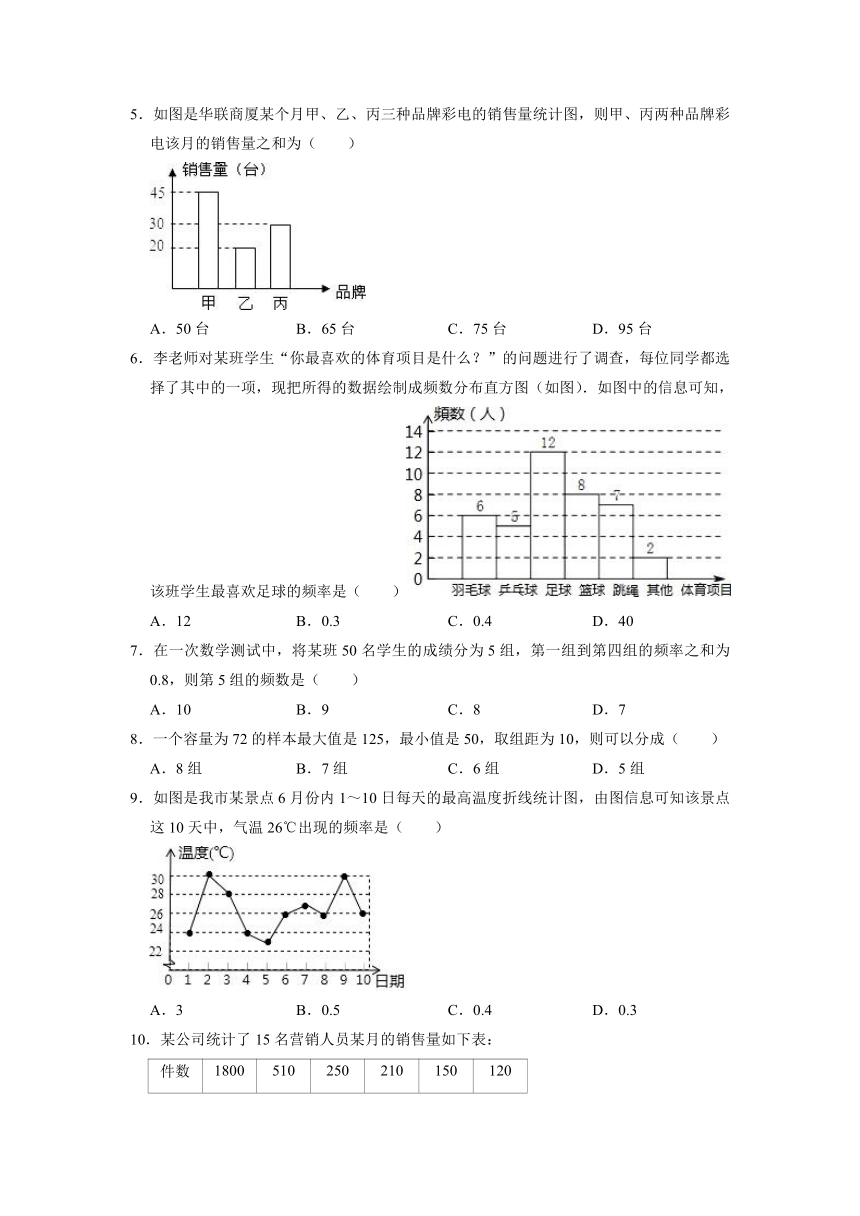
5.如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
A.50台 B.65台 C.75台 D.95台
6.李老师对某班学生“你最喜欢的体育项目是什么?”的问题进行了调查,每位同学都选择了其中的一项,现把所得的数据绘制成频数分布直方图(如图).如图中的信息可知,该班学生最喜欢足球的频率是( )
A.12 B.0.3 C.0.4 D.40
7.在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.10 B.9 C.8 D.7
8.一个容量为72的样本最大值是125,最小值是50,取组距为10,则可以分成( )
A.8组 B.7组 C.6组 D.5组
9.如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
10.某公司统计了15名营销人员某月的销售量如下表:
件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
根据以上信息,该公司计划制定下月销售定额,这个销售定额应为( )
A.120件 B.210件 C.320件 D.1800件
二、填空题(共5小题)
11.八年级(1)班全体学生参加了学校举办的安全知识竞赛,如图是该班学生竞赛成绩的频数分布直方图(满分为100分,成绩均为整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全班人数的百分比是 .
12.“Iamagoodstudent.”这句话的所有字母中,字母“a”出现的频率是
13.一个样本有100个数据,最大的是351,最小的是75,组距为25,可分为 组.
14.地铁某换乘站设有编号为A,B,C,D,E的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 A,B B,C C,D D,E A,E
疏散乘客时间(s) 120 220 160 140 200
则疏散乘客最快的一个安全出口的编号是 .
15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是 .
三、解答题(共5小题)
16.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分) 频数 百分比
60≤x<70 30 10%
70≤x<80 90 n
80≤x<90 m 40%
90≤x≤100 60 20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= ;n= ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 .
17.某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.
(1)学校采用的调查方法是 .
(2)求“踢毽子”的人数,并在下图中将“踢毽子”部分的条形图补充完整.
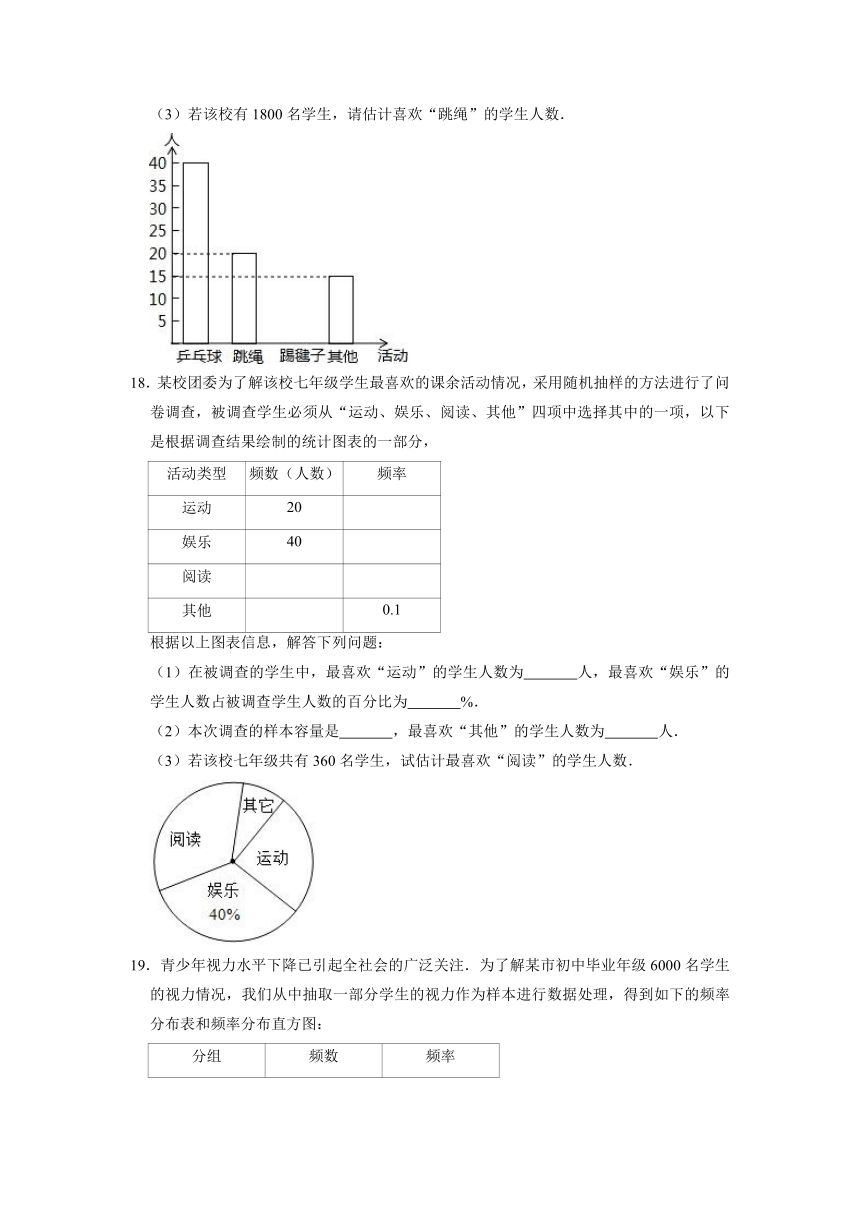
(3)若该校有1800名学生,请估计喜欢“跳绳”的学生人数.
18.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
19.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
20.李强靠勤工捡学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):
星期 一 二 三 四 五 六 日
收入 +15 +18 0 +16 0 +25 +24
支出 ﹣10 ﹣14 ﹣13 ﹣8 ﹣10 ﹣14 ﹣15
(1)到这个周末,李强有多少节余?
(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
专题05 : 2021年北师大新版七年级(上) 6.3 数据的表示 - 期末复习专题训练
参考答案与试题解析
一、选择题(共10小题)
1.某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
【解答】解:A、得分在70~80分之间的人数最多,故正确;
B、2+4+8+12+14=40(人),该班的总人数为40人,故正确;
C、得分在90~100分之间的人数最少,有2人,故正确;
D、40﹣4=36(人),及格(≥60分)人数是36人,故D错误,故选D.
2.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图所示,该调查的方式是( ),图中的a的值是( )
A.全面调查,26 B.全面调查,24
C.抽样调查,26 D.抽样调查,24
【解答】解:该调查方式是抽样调查,
a=50﹣6﹣10﹣6﹣4=24,
故选:D.
3.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
【解答】解:仰卧起坐个数不少于50个的有52、50、50、61、72共5个,
所以,频率==0.5.
故选:C.
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
【解答】解:∵样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,
∴第二小组和第三小组的频数为:30×=12,30×=9,
∴第二小组和第三小组的频率分别为:=0.4,=0.3.
故选:A.
5.如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
A.50台 B.65台 C.75台 D.95台
【解答】解:甲、丙两品牌彩电销量之和为45+30=75(台).
故选:C.
6.李老师对某班学生“你最喜欢的体育项目是什么?”的问题进行了调查,每位同学都选择了其中的一项,现把所得的数据绘制成频数分布直方图(如图).如图中的信息可知,该班学生最喜欢足球的频率是( )
A.12 B.0.3 C.0.4 D.40
【解答】解:读图可知:共有(6+5+12+8+7+2)=40人,
最喜欢足球的频数为12,是最喜欢篮球的频率是=0.3,
故选:B.
7.在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.10 B.9 C.8 D.7
【解答】解:∵第一组到第四组的频率之和为0.8,
∴第五组的频率为1﹣0.8=0.2,
则第五组的频数为50×0.2=10,
故选:A.
8.一个容量为72的样本最大值是125,最小值是50,取组距为10,则可以分成( )
A.8组 B.7组 C.6组 D.5组
【解答】解:在样本数据中最大值为125,最小值是50,它们的差是125﹣50=75,
已知组距为10,那么由于 75÷10=7.5,
故可以分成8组.
故选:A.
9.如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
【解答】解:由折线统计图知,气温26℃出现的天数为3天,
∴气温26℃出现的频率是3÷10=0.3,
故选:D.
10.某公司统计了15名营销人员某月的销售量如下表:
件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
根据以上信息,该公司计划制定下月销售定额,这个销售定额应为( )
A.120件 B.210件 C.320件 D.1800件
【解答】解:在这15名营销人员销售量中,销售额达到210件的有1+1+3+5=10(人),
大部分人达到这一营业目标,
故选:B.
二、填空题(共5小题)
11.八年级(1)班全体学生参加了学校举办的安全知识竞赛,如图是该班学生竞赛成绩的频数分布直方图(满分为100分,成绩均为整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全班人数的百分比是 30% .
【解答】解:总人数是:5+10+20+15=50(人),优秀的人数是:15人,
则该班这次成绩达到优秀的人数占全班人数的百分比是:×100%=30%.
故答案是:30%.
12.“Iamagoodstudent.”这句话的所有字母中,字母“a”出现的频率是
【解答】解:“Iamagoodstudent”这个句子里共有15个字母,字母“a”出现2次,
故频率为,
故答案为:.
13.一个样本有100个数据,最大的是351,最小的是75,组距为25,可分为 12 组.
【解答】解:在样本数据中最大值为351,最小值为75,它们的差是351﹣75=276,已知组距为25,那么由于276÷25=11.04,故可以分成12组.
故答案为:12.
14.地铁某换乘站设有编号为A,B,C,D,E的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 A,B B,C C,D D,E A,E
疏散乘客时间(s) 120 220 160 140 200
则疏散乘客最快的一个安全出口的编号是 D .
【解答】解:同时开放A、E两个安全出口,疏散1000名乘客所需的时间为200s,
同时开放D、E两个安全出口,疏散1000名乘客所需的时间为140s,
得到D疏散乘客比A快;
同时开放A、E两个安全出口,疏散1000名乘客所需的时间为200s,
同时开放A、B两个安全出口,疏散1000名乘客所需的时间为120s,
得到B疏散乘客比E快;
同时开放A、B两个安全出口,疏散1000名乘客所需的时间为120s,
同时开放B、C两个安全出口,疏散1000名乘客所需的时间为220s,
得到A疏散乘客比C快;
同时开放B、C两个安全出口,疏散1000名乘客所需的时间为220s,
同时开放C、D两个安全出口,疏散1000名乘客所需的时间为160s,
得到D疏散乘客比B快.
综上,疏散乘客最快的一个安全出口的编号是D.
故答案为:D.
15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是 120 .
【解答】解:根据题中的数据得:1200×=120,
则该校1200名学生一周的课外阅读时间为8小时的人数是120.
故答案为:120
三、解答题(共5小题)
16.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分) 频数 百分比
60≤x<70 30 10%
70≤x<80 90 n
80≤x<90 m 40%
90≤x≤100 60 20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 300 ;
(2)在表中:m= 120 ;n= 30% ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 18000人 .
【解答】解:(1)30÷10%=300(人),
故答案为300;
(2)m=300×40%=120(人),n=90÷300=30%,
故答案为:120,30%;
(3)根据频数,画出频数分布直方图;
(4)30000×(40%+20%)=18000(人),
故答案为:18000人.
17.某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.
(1)学校采用的调查方法是 抽样调查 .
(2)求“踢毽子”的人数,并在下图中将“踢毽子”部分的条形图补充完整.
(3)若该校有1800名学生,请估计喜欢“跳绳”的学生人数.
【解答】解:(1)学校采用的调查方法是:抽样调查;
(2)踢毽子的人数是:100﹣40﹣20﹣15=25(人),
;
(3)喜欢“跳绳”的学生人数是:1800×=360(人).
18.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 20 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 40 %.
(2)本次调查的样本容量是 100 ,最喜欢“其他”的学生人数为 10 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
【解答】解:(1)从统计图表中,可得最喜欢“运动”的有20人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为40%,
故答案为:20,40;
(2)40÷40%=100(人),100×0.1=10(人),
故答案为:100,10;
(3)360×=108(人),
答:该校七年级360名学生中最喜欢“阅读”的学生有108人.
19.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
【解答】解:(1)样本容量=2÷0.04=50,
4.55﹣4.85的频数=50×0.40=20;
如图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 20 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 50 1
(2)6000×(0.04+0.16+0.40)=3600(名),
∴约有3600名学生的视力需要矫正.
20.李强靠勤工捡学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):
星期 一 二 三 四 五 六 日
收入 +15 +18 0 +16 0 +25 +24
支出 ﹣10 ﹣14 ﹣13 ﹣8 ﹣10 ﹣14 ﹣15
(1)到这个周末,李强有多少节余?
(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
【解答】解:(1)由题意可得:15+18+16+25+24﹣10﹣14﹣13﹣8﹣10﹣14﹣15=14元;
(2)由题意得:14÷7×30=60元;
(3)根据题意得;84÷7×30=360元.
一、选择题(共10小题)
1.某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
2.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图所示,该调查的方式是( ),图中的a的值是( )
A.全面调查,26 B.全面调查,24
C.抽样调查,26 D.抽样调查,24
3.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
5.如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
A.50台 B.65台 C.75台 D.95台
6.李老师对某班学生“你最喜欢的体育项目是什么?”的问题进行了调查,每位同学都选择了其中的一项,现把所得的数据绘制成频数分布直方图(如图).如图中的信息可知,该班学生最喜欢足球的频率是( )
A.12 B.0.3 C.0.4 D.40
7.在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.10 B.9 C.8 D.7
8.一个容量为72的样本最大值是125,最小值是50,取组距为10,则可以分成( )
A.8组 B.7组 C.6组 D.5组
9.如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
10.某公司统计了15名营销人员某月的销售量如下表:
件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
根据以上信息,该公司计划制定下月销售定额,这个销售定额应为( )
A.120件 B.210件 C.320件 D.1800件
二、填空题(共5小题)
11.八年级(1)班全体学生参加了学校举办的安全知识竞赛,如图是该班学生竞赛成绩的频数分布直方图(满分为100分,成绩均为整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全班人数的百分比是 .
12.“Iamagoodstudent.”这句话的所有字母中,字母“a”出现的频率是
13.一个样本有100个数据,最大的是351,最小的是75,组距为25,可分为 组.
14.地铁某换乘站设有编号为A,B,C,D,E的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 A,B B,C C,D D,E A,E
疏散乘客时间(s) 120 220 160 140 200
则疏散乘客最快的一个安全出口的编号是 .
15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是 .
三、解答题(共5小题)
16.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分) 频数 百分比
60≤x<70 30 10%
70≤x<80 90 n
80≤x<90 m 40%
90≤x≤100 60 20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 ;
(2)在表中:m= ;n= ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 .
17.某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.
(1)学校采用的调查方法是 .
(2)求“踢毽子”的人数,并在下图中将“踢毽子”部分的条形图补充完整.
(3)若该校有1800名学生,请估计喜欢“跳绳”的学生人数.
18.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 %.
(2)本次调查的样本容量是 ,最喜欢“其他”的学生人数为 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
19.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
20.李强靠勤工捡学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):
星期 一 二 三 四 五 六 日
收入 +15 +18 0 +16 0 +25 +24
支出 ﹣10 ﹣14 ﹣13 ﹣8 ﹣10 ﹣14 ﹣15
(1)到这个周末,李强有多少节余?
(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
专题05 : 2021年北师大新版七年级(上) 6.3 数据的表示 - 期末复习专题训练
参考答案与试题解析
一、选择题(共10小题)
1.某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
【解答】解:A、得分在70~80分之间的人数最多,故正确;
B、2+4+8+12+14=40(人),该班的总人数为40人,故正确;
C、得分在90~100分之间的人数最少,有2人,故正确;
D、40﹣4=36(人),及格(≥60分)人数是36人,故D错误,故选D.
2.为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图所示,该调查的方式是( ),图中的a的值是( )
A.全面调查,26 B.全面调查,24
C.抽样调查,26 D.抽样调查,24
【解答】解:该调查方式是抽样调查,
a=50﹣6﹣10﹣6﹣4=24,
故选:D.
3.在一次体育测试中,10名女生完成仰卧起坐的个数如下:38,52,47,46,50,50,61,72,45,48.则这10名女生仰卧起坐个数不少于50个的频率为( )
A.0.3 B.0.4 C.0.5 D.0.6
【解答】解:仰卧起坐个数不少于50个的有52、50、50、61、72共5个,
所以,频率==0.5.
故选:C.
4.已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )
A.0.4和0.3 B.0.4和9 C.12和0.3 D.12和9
【解答】解:∵样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,
∴第二小组和第三小组的频数为:30×=12,30×=9,
∴第二小组和第三小组的频率分别为:=0.4,=0.3.
故选:A.
5.如图是华联商厦某个月甲、乙、丙三种品牌彩电的销售量统计图,则甲、丙两种品牌彩电该月的销售量之和为( )
A.50台 B.65台 C.75台 D.95台
【解答】解:甲、丙两品牌彩电销量之和为45+30=75(台).
故选:C.
6.李老师对某班学生“你最喜欢的体育项目是什么?”的问题进行了调查,每位同学都选择了其中的一项,现把所得的数据绘制成频数分布直方图(如图).如图中的信息可知,该班学生最喜欢足球的频率是( )
A.12 B.0.3 C.0.4 D.40
【解答】解:读图可知:共有(6+5+12+8+7+2)=40人,
最喜欢足球的频数为12,是最喜欢篮球的频率是=0.3,
故选:B.
7.在一次数学测试中,将某班50名学生的成绩分为5组,第一组到第四组的频率之和为0.8,则第5组的频数是( )
A.10 B.9 C.8 D.7
【解答】解:∵第一组到第四组的频率之和为0.8,
∴第五组的频率为1﹣0.8=0.2,
则第五组的频数为50×0.2=10,
故选:A.
8.一个容量为72的样本最大值是125,最小值是50,取组距为10,则可以分成( )
A.8组 B.7组 C.6组 D.5组
【解答】解:在样本数据中最大值为125,最小值是50,它们的差是125﹣50=75,
已知组距为10,那么由于 75÷10=7.5,
故可以分成8组.
故选:A.
9.如图是我市某景点6月份内1~10日每天的最高温度折线统计图,由图信息可知该景点这10天中,气温26℃出现的频率是( )
A.3 B.0.5 C.0.4 D.0.3
【解答】解:由折线统计图知,气温26℃出现的天数为3天,
∴气温26℃出现的频率是3÷10=0.3,
故选:D.
10.某公司统计了15名营销人员某月的销售量如下表:
件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
根据以上信息,该公司计划制定下月销售定额,这个销售定额应为( )
A.120件 B.210件 C.320件 D.1800件
【解答】解:在这15名营销人员销售量中,销售额达到210件的有1+1+3+5=10(人),
大部分人达到这一营业目标,
故选:B.
二、填空题(共5小题)
11.八年级(1)班全体学生参加了学校举办的安全知识竞赛,如图是该班学生竞赛成绩的频数分布直方图(满分为100分,成绩均为整数),若将成绩不低于90分的评为优秀,则该班这次成绩达到优秀的人数占全班人数的百分比是 30% .
【解答】解:总人数是:5+10+20+15=50(人),优秀的人数是:15人,
则该班这次成绩达到优秀的人数占全班人数的百分比是:×100%=30%.
故答案是:30%.
12.“Iamagoodstudent.”这句话的所有字母中,字母“a”出现的频率是
【解答】解:“Iamagoodstudent”这个句子里共有15个字母,字母“a”出现2次,
故频率为,
故答案为:.
13.一个样本有100个数据,最大的是351,最小的是75,组距为25,可分为 12 组.
【解答】解:在样本数据中最大值为351,最小值为75,它们的差是351﹣75=276,已知组距为25,那么由于276÷25=11.04,故可以分成12组.
故答案为:12.
14.地铁某换乘站设有编号为A,B,C,D,E的五个安全出口.若同时开放其中的两个安全出口,疏散1000名乘客所需的时间如下:
安全出口编号 A,B B,C C,D D,E A,E
疏散乘客时间(s) 120 220 160 140 200
则疏散乘客最快的一个安全出口的编号是 D .
【解答】解:同时开放A、E两个安全出口,疏散1000名乘客所需的时间为200s,
同时开放D、E两个安全出口,疏散1000名乘客所需的时间为140s,
得到D疏散乘客比A快;
同时开放A、E两个安全出口,疏散1000名乘客所需的时间为200s,
同时开放A、B两个安全出口,疏散1000名乘客所需的时间为120s,
得到B疏散乘客比E快;
同时开放A、B两个安全出口,疏散1000名乘客所需的时间为120s,
同时开放B、C两个安全出口,疏散1000名乘客所需的时间为220s,
得到A疏散乘客比C快;
同时开放B、C两个安全出口,疏散1000名乘客所需的时间为220s,
同时开放C、D两个安全出口,疏散1000名乘客所需的时间为160s,
得到D疏散乘客比B快.
综上,疏散乘客最快的一个安全出口的编号是D.
故答案为:D.
15.在开展“国学诵读”活动中,某校为了解全校1200名学生课外阅读的情况,随机调查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据,估计该校1200名学生一周的课外阅读时间为8小时的人数是 120 .
【解答】解:根据题中的数据得:1200×=120,
则该校1200名学生一周的课外阅读时间为8小时的人数是120.
故答案为:120
三、解答题(共5小题)
16.为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
分数x(分) 频数 百分比
60≤x<70 30 10%
70≤x<80 90 n
80≤x<90 m 40%
90≤x≤100 60 20%
请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为 300 ;
(2)在表中:m= 120 ;n= 30% ;
(3)根据频数分布表画频数分布直方图;
(4)如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 18000人 .
【解答】解:(1)30÷10%=300(人),
故答案为300;
(2)m=300×40%=120(人),n=90÷300=30%,
故答案为:120,30%;
(3)根据频数,画出频数分布直方图;
(4)30000×(40%+20%)=18000(人),
故答案为:18000人.
17.某校为开展“阳光体育”运动,丰富学生课间自由活动内容,随机选取了本校100名学生进行调查,调查的内容是:你最喜欢的自由活动项目是什么?并将收集到的数据整理,绘出了如图所示的统计图.
(1)学校采用的调查方法是 抽样调查 .
(2)求“踢毽子”的人数,并在下图中将“踢毽子”部分的条形图补充完整.
(3)若该校有1800名学生,请估计喜欢“跳绳”的学生人数.
【解答】解:(1)学校采用的调查方法是:抽样调查;
(2)踢毽子的人数是:100﹣40﹣20﹣15=25(人),
;
(3)喜欢“跳绳”的学生人数是:1800×=360(人).
18.某校团委为了解该校七年级学生最喜欢的课余活动情况,采用随机抽样的方法进行了问卷调查,被调查学生必须从“运动、娱乐、阅读、其他”四项中选择其中的一项,以下是根据调查结果绘制的统计图表的一部分,
活动类型 频数(人数) 频率
运动 20
娱乐 40
阅读
其他 0.1
根据以上图表信息,解答下列问题:
(1)在被调查的学生中,最喜欢“运动”的学生人数为 20 人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为 40 %.
(2)本次调查的样本容量是 100 ,最喜欢“其他”的学生人数为 10 人.
(3)若该校七年级共有360名学生,试估计最喜欢“阅读”的学生人数.
【解答】解:(1)从统计图表中,可得最喜欢“运动”的有20人,最喜欢“娱乐”的学生人数占被调查学生人数的百分比为40%,
故答案为:20,40;
(2)40÷40%=100(人),100×0.1=10(人),
故答案为:100,10;
(3)360×=108(人),
答:该校七年级360名学生中最喜欢“阅读”的学生有108人.
19.青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况,我们从中抽取一部分学生的视力作为样本进行数据处理,得到如下的频率分布表和频率分布直方图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 1
(1)根据上述数据,补全频率分布表和频率分布直方图;
(2)若视力在4.85以上属于正常,不需矫正,试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正.
【解答】解:(1)样本容量=2÷0.04=50,
4.55﹣4.85的频数=50×0.40=20;
如图:
分组 频数 频率
3.95~4.25 2 0.04
4.25~4.55 8 0.16
4.55~4.85 20 0.40
4.85~5.15 16 0.32
5.15~5.45 4 0.08
合计 50 1
(2)6000×(0.04+0.16+0.40)=3600(名),
∴约有3600名学生的视力需要矫正.
20.李强靠勤工捡学的收入维持上大学费用,表中是李强某一周的收支情况表,记收入为正,支出为负(单位:元):
星期 一 二 三 四 五 六 日
收入 +15 +18 0 +16 0 +25 +24
支出 ﹣10 ﹣14 ﹣13 ﹣8 ﹣10 ﹣14 ﹣15
(1)到这个周末,李强有多少节余?
(2)照这个情况估计,李强一个月(按30天计算)能有多少节余?
(3)按以上的支出水平,李强一个月(按30天计算)至少有多少收入才能维持正常开支?
【解答】解:(1)由题意可得:15+18+16+25+24﹣10﹣14﹣13﹣8﹣10﹣14﹣15=14元;
(2)由题意得:14÷7×30=60元;
(3)根据题意得;84÷7×30=360元.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
