小学数学北师大版六年级下1.6 圆柱的体积课件(共14张PPT)
文档属性
| 名称 | 小学数学北师大版六年级下1.6 圆柱的体积课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 07:30:34 | ||
图片预览





文档简介
(共14张PPT)
一
圆柱与圆锥
第6课时 圆柱的体积(2)
北师版数学六年级下册
两个一样的水龙头同时往两个圆柱形容器里注水,哪个容器先装满呢?
我比你粗些,我装的水多!
不对,我比你高,我装的水多。
你知道他们谁说得对吗!
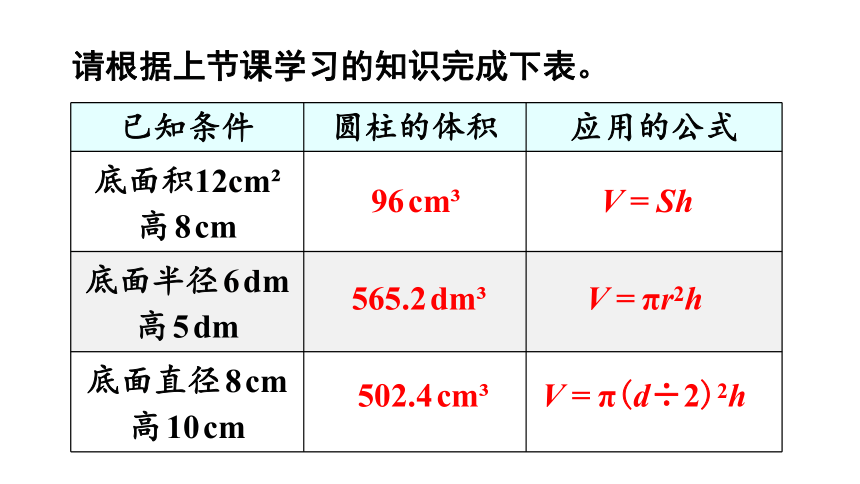
请根据上节课学习的知识完成下表。
已知条件 圆柱的体积 应用的公式
底面积12cm 高8cm
底面半径6dm高5dm
底面直径8cm高10cm
96cm
565.2dm
502.4cm
V=Sh
V =πr2h
V =π(d÷2)2h
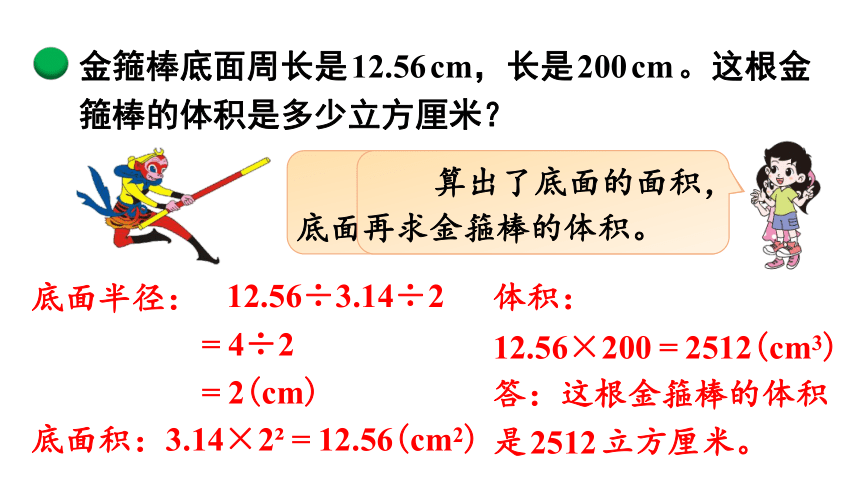
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
要先算出底面的面积,再求金箍棒的体积。
可以根据底面的周长求底面的半径,再求底面面积。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
可以根据底面的周长求底面的半径,再求底面面积。
底面半径:
12.56÷3.14÷2
=4÷2
=2(cm)
底面积:
3.14×2 =12.56(cm2)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512立方厘米。
算出了底面的面积,再求金箍棒的体积。
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8 (g)
答:这根金箍棒重19.8448千克。
=19.8448(kg)
不要忘了换算单位哦!
1. 光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2 )2×4
答:挖出了3.14立方米的土。
=3.14(m3)
=3.14 ×(0.25×4)
=3.14 ×1
求挖出了多少立方米的土就是求这个圆柱形水井的体积。
2. 下面的长方体和圆柱哪个体积大?说说你的比较方法。
圆柱体积:3.14×2 ×6=75.36(dm3)
长方体体积:4×4×6=96(dm3)
96>75.36 长方体的体积大
16dm
12.56dm
16>12.56 长方体的体积大
高相等的长方体和圆柱体的体积关系:
底面积大的体积就大。
3. 将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱的高大约是多少?
6×6×6
=36×6
=216(dm2)
3.14×32=28.26(dm2)
216÷28.26≈7.64(dm)
答:这个圆柱的高大约是7.64分米。
正方体的体积等于圆柱的体积。
4. 把一个棱长6分米的正方体木块削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=169.56(dm3)
答:这个圆柱的体积是169.56立方分米。
正方体的棱长=圆柱的直径和高
如图,求出小铁块的体积。
2cm
2cm
10cm
3.14×(10÷2)2×2
=3.14×25×2
=3.14×50
=15.7(cm3)
答:小铁块的体积为15.7立方厘米。
圆柱体积的实际应用
1. 已知圆柱的底面周长和高,求圆柱的体积:
先根据周长求出半径:r=C÷π÷2
再求出底面积: S=π(C÷π÷2)
最后再求出体积:V=π(C÷π÷2) h
2. 高相等的长方体和圆柱体的体积关系:
底面积大的体积就大。
3. 解决圆柱体积的实际问题:我们常常把一
个体积转化成另一个体积:如正方体溶铸 成圆柱体;小石子放入水中水面升高等等。
课后作业
1. 一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为
80cm。每立方米稻谷的质量约为700kg,这个粮囤存
放的稻谷的质量约为多少千克?
2. 请你设计一个方案,测量并计算出1枚1元硬币的体积。
一
圆柱与圆锥
第6课时 圆柱的体积(2)
北师版数学六年级下册
两个一样的水龙头同时往两个圆柱形容器里注水,哪个容器先装满呢?
我比你粗些,我装的水多!
不对,我比你高,我装的水多。
你知道他们谁说得对吗!
请根据上节课学习的知识完成下表。
已知条件 圆柱的体积 应用的公式
底面积12cm 高8cm
底面半径6dm高5dm
底面直径8cm高10cm
96cm
565.2dm
502.4cm
V=Sh
V =πr2h
V =π(d÷2)2h
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
要先算出底面的面积,再求金箍棒的体积。
可以根据底面的周长求底面的半径,再求底面面积。
金箍棒底面周长是12.56cm,长是200cm。这根金箍棒的体积是多少立方厘米?
可以根据底面的周长求底面的半径,再求底面面积。
底面半径:
12.56÷3.14÷2
=4÷2
=2(cm)
底面积:
3.14×2 =12.56(cm2)
体积:
12.56×200=2512(cm3)
答:这根金箍棒的体积是2512立方厘米。
算出了底面的面积,再求金箍棒的体积。
如果这根金箍棒是铁制的,每立方厘米铁的质量为7.9g,这根金箍棒的质量为多少千克?
7.9×2512=19844.8 (g)
答:这根金箍棒重19.8448千克。
=19.8448(kg)
不要忘了换算单位哦!
1. 光明村李大伯家挖一口圆柱形的水井,底面周长是3.14m,深是4m。挖出了多少立方米的土?
3.14×(3.14÷3.14÷2 )2×4
答:挖出了3.14立方米的土。
=3.14(m3)
=3.14 ×(0.25×4)
=3.14 ×1
求挖出了多少立方米的土就是求这个圆柱形水井的体积。
2. 下面的长方体和圆柱哪个体积大?说说你的比较方法。
圆柱体积:3.14×2 ×6=75.36(dm3)
长方体体积:4×4×6=96(dm3)
96>75.36 长方体的体积大
16dm
12.56dm
16>12.56 长方体的体积大
高相等的长方体和圆柱体的体积关系:
底面积大的体积就大。
3. 将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱的高大约是多少?
6×6×6
=36×6
=216(dm2)
3.14×32=28.26(dm2)
216÷28.26≈7.64(dm)
答:这个圆柱的高大约是7.64分米。
正方体的体积等于圆柱的体积。
4. 把一个棱长6分米的正方体木块削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
3.14×(6÷2)2×6
=3.14×9×6
=169.56(dm3)
答:这个圆柱的体积是169.56立方分米。
正方体的棱长=圆柱的直径和高
如图,求出小铁块的体积。
2cm
2cm
10cm
3.14×(10÷2)2×2
=3.14×25×2
=3.14×50
=15.7(cm3)
答:小铁块的体积为15.7立方厘米。
圆柱体积的实际应用
1. 已知圆柱的底面周长和高,求圆柱的体积:
先根据周长求出半径:r=C÷π÷2
再求出底面积: S=π(C÷π÷2)
最后再求出体积:V=π(C÷π÷2) h
2. 高相等的长方体和圆柱体的体积关系:
底面积大的体积就大。
3. 解决圆柱体积的实际问题:我们常常把一
个体积转化成另一个体积:如正方体溶铸 成圆柱体;小石子放入水中水面升高等等。
课后作业
1. 一个装满稻谷的圆柱形粮囤,底面面积为2m2,高为
80cm。每立方米稻谷的质量约为700kg,这个粮囤存
放的稻谷的质量约为多少千克?
2. 请你设计一个方案,测量并计算出1枚1元硬币的体积。
