吉林省长春市重点高中2022届高三上学期12月第二学程考试数学(理)试题(Word版含答案)
文档属性
| 名称 | 吉林省长春市重点高中2022届高三上学期12月第二学程考试数学(理)试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 00:00:00 | ||
图片预览



文档简介
长春市重点高中2022届高三上学期12月第二学程考试
理科数学试题
第Ⅰ卷(共60 分)
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.记全集,设集合,,则( )
A. B.
C. D.
2.若复数满足,则的虚部为( )
A. B. C. D.
3.已知空间中的两个不同的平面,,直线平面,则“”是“”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分又不必要条件
4.一个正棱柱的正视图和俯视图如图所示(单位:),则该三棱柱侧视图的面积(单位:)是( )
A. B.2 C. D.
5.已知向量,,若,则向量与的夹角等于( )
A. B. C. D.
6.曲线在处的切线的倾斜角为,则( )
A. B. C. D.
7.设等差数列{an}的前n项和为Sn,若S15>0,S16<0,则数列的前15项中最大的项是( )
A.第1项 B.第8项 C.第9项 D.第15项
8.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,四个面均为直角三角形的四面体称为“鳖臑”,如图在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积最大为
D.过A点分别作于点E,于点F,则
9.在△中,,,,,且点是的中点,则( )
A. B. C. D.
10.已知函数实数a,b满足不等式,则下列不等式成立的是( )
A. B. C. D.
11.已知函数,下列结论中正确的个数是( )
①的图象关于中心对称;②的图象关于对称;③的最大值为;④既是奇函数,又是周期函数.
A.1个 B.2个 C.3个 D.4个
12.用符号表示不超过的最大整数,例如:,,.设函数有三个零点,且,则的取值范围是( )
A. B.
C. D. QUOTE QUOTE
第Ⅱ卷(共 90 分)
二、填空题:本题共4小题,每小题5分,共20分.
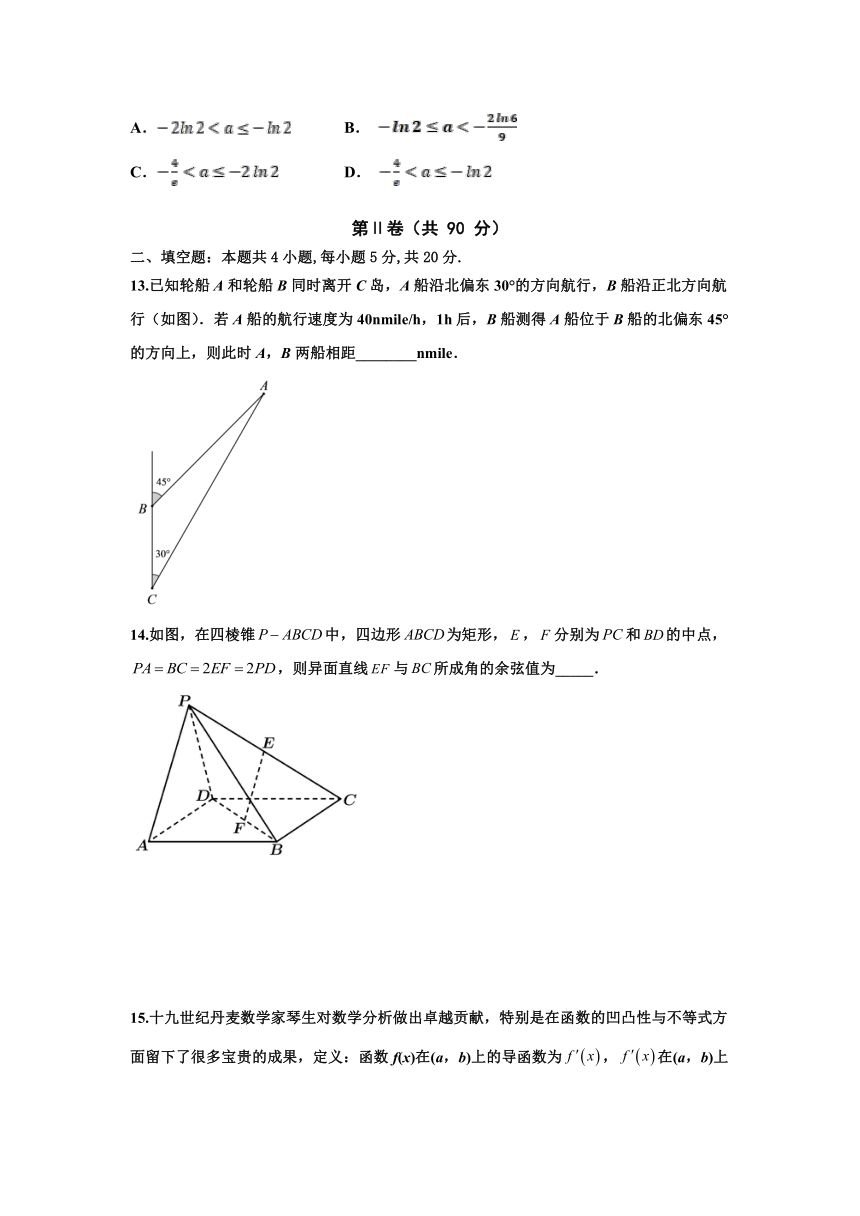
13.已知轮船A和轮船B同时离开C岛,A船沿北偏东30°的方向航行,B船沿正北方向航行(如图).若A船的航行速度为40nmile/h,1h后,B船测得A船位于B船的北偏东45°的方向上,则此时A,B两船相距________nmile.
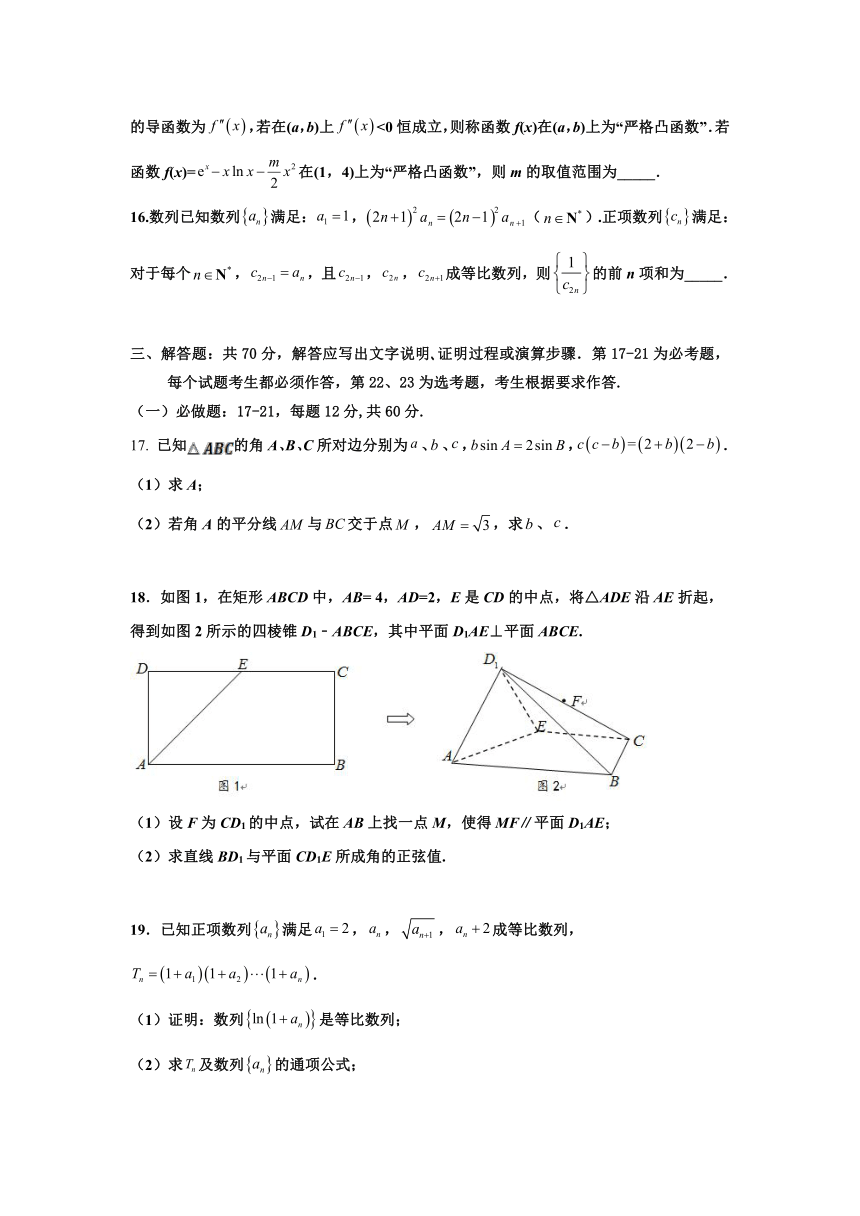
14.如图,在四棱锥中,四边形为矩形,,分别为和的中点,,则异面直线与所成角的余弦值为_____.
15.十九世纪丹麦数学家琴生对数学分析做出卓越贡献,特别是在函数的凹凸性与不等式方面留下了很多宝贵的成果,定义:函数f(x)在(a,b)上的导函数为,在(a,b)上的导函数为,若在(a,b)上<0恒成立,则称函数f(x)在(a,b)上为“严格凸函数”.若函数f(x)=在(1,4)上为“严格凸函数”,则m的取值范围为_____.
16.数列已知数列满足:,().正项数列满足:对于每个,,且,,成等比数列,则的前n项和为_____.
三、解答题:共70分,解答应写出文字说明 证明过程或演算步骤.第17-21为必考题,每个试题考生都必须作答,第22、23为选考题,考生根据要求作答.
(一)必做题:17-21,每题12分,共60分.
17. 已知的角A、B、C所对边分别为、、,,.
(1)求A;
(2)若角A的平分线与交于点,,求、.
18.如图1,在矩形ABCD中,AB= 4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1﹣ABCE,其中平面D1AE⊥平面ABCE.
(1)设F为CD1的中点,试在AB上找一点M,使得MF∥平面D1AE;
(2)求直线BD1与平面CD1E所成角的正弦值.
19.已知正项数列满足,,,成等比数列,.
(1)证明:数列是等比数列;
(2)求及数列的通项公式;
(3)若,求数列的前n项和
20.已知点在抛物线上,过点的直线与抛物线C有两个不同的交点A、B,且直线PA交轴于M,直线PB交轴于N.
(1)求直线的斜率的取值范围;
(2)设O为原点,,试判断是否为定值,若是,求值;若不是,求的取值范围.
21.已知函数,.
(1)当时,设,求证:;
(2)若恰有两个零点,求的最小整数值.
(二)选做题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
[选修4-4:坐标系与参数方程](10分)
22.在平面直角坐标系中,的参数方程为(为参数,),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,的极坐标方程为.
(1)求的直角坐标方程;
(2)与相交于不同两点、,线段中点为,点,若,求参数方程中的值.
[选修4-5:不等式选讲](10分)
23.已知函数.
(1)当时,求函数的最小值;
(2)若的解集为,且,求的最小值.
长春市重点高中2022届高三上学期12月第二学程考试
数学试卷答案
一、单选题
1.A 2.C 3.B 4.D 5.A 6.B 7.B 8.C 9.A 10.C 11.C12.B
二、填空题
13.【答案】 14.【答案】
15.【答案】 16.【答案】
3、解答题
17.(1)(2)
(1)由正弦定理及得,,
,即,所以,,
所以,,
,所以,.
(2)解:是角的平分线,,
,即,
,①,由(1)知,②
由①②解得.
18.【答案】(1)AM=;(2).
【详解】
(1)取D1E的中点N,连AN、NF,则,
∵,当AM=时,,
则且,则AMFN是平行四边形,AN∥MF.
又平面D1AE,平面D1AE,则MF∥平面D1AE.
(2)分别取AE、AB、BC的中点O、G、K,连OD1、OM、OK、EG,
∵AD1=ED1=2,∴OD1⊥AE,又平面D1AE⊥平面ABCE且交于AE,
∴OD1⊥平面ABCE.易知OK∥AB,OM∥EG∥BC,又AB⊥BC,∴OM⊥OK,
故如图建系O﹣xyz.
设平面CD1E的法向量 =(x, y, z),
∵EC∥y轴,∴,
∵,
∴D1为(0, 0,),又E为(﹣1, 1, 0),则,
由,取,则=(, 0, 1).
又B为(1, 3, 0),则,
记直线BD1与平面CD1E所成角的大小为,
则.
19.【答案】(1)证明见解析(2);(3);【分析】
小问1:由题意得,两边取对数可得,即可证明;
小问2:由(1)知,所以,即可求解;
小问3:由可化为,所以,结合小问2即可求证明.
(1)
因为,,成等比数列,所以,
所以因为,所以,
将式两边取对数,得,即,
所以,数列是首项为,公比为2的等比数列
(2)由(1)知,所以,所以
所以
(3)因为,即①;
又因为,所以,即②;
①式代入②式消去,可得
所以
因为,,则,所以
20.【答案】
(1)(3)定值为2
(1)
因点在抛物线上,则,解得,
所以抛物线C的方程为.
令直线的斜率为k,则直线方程为:,
由消去y并整理得:,
因直线与抛物线C有两个不同的交点A、B,则,解得且,
又直线PA,PB与相交,而点(1,-2)在抛物线C上,则直线不能过点(1,-2),
否则PA或PB之一平行于y轴,矛盾,因此,
综上得:,且,
所以直线的斜率的取值范围.
(2)设点,,,而,则,同理,
设,由(2)知,
直线方程:,即,则,
令,得,同理,
于是得
,
所以为定值2.
【点睛】方法点睛:求定值问题常见的方法有两种:(1)从特殊入手,求出定值,再证明这个值与变量无关;
(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
21.【答案】(1)证明见解析;(2)2.
(1)当时,,
则,
因为, 所以,
所以,所以函数在上为增函数,
所以;
(2)当时,,设,
因为,所以,
所以,所以函数无零点,
当时,设, 因为,
所以, 即,
,
所以函数无零点
当时,,
设,,
所以函数在上为减函数,
又,,
所以在上存在零点,使,
当时,,当时,,
函数在上为增函数,在上为减函数,
因为,,
,
所以函数在,各一个零点,
综上所述:当时,恰有两个零点,当时,,
所以时,是恰有两个零点的最小整数值 .
22.【答案】(1)(2)或
(1)
解:由得,所以,
将代入得,即,
所以的直角坐标方程为;
(2)
解:将代入整理得
设、对应的参数分别为、,则、是方程的两根,
所以,因为,所以,所以,此时,
所以,所以,所以或.
23.【答案】(1)6 (2)【分析】
(1)解:当时,,所以,当时等号成立
∴函数的最小值为6.
(2)解:由得,
因为的解集为,∴,解得,∴,
(当且仅当时取等号),
(当且仅当时取等号),的最小值为.
理科数学试题
第Ⅰ卷(共60 分)
一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.记全集,设集合,,则( )
A. B.
C. D.
2.若复数满足,则的虚部为( )
A. B. C. D.
3.已知空间中的两个不同的平面,,直线平面,则“”是“”的( )
A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分又不必要条件
4.一个正棱柱的正视图和俯视图如图所示(单位:),则该三棱柱侧视图的面积(单位:)是( )
A. B.2 C. D.
5.已知向量,,若,则向量与的夹角等于( )
A. B. C. D.
6.曲线在处的切线的倾斜角为,则( )
A. B. C. D.
7.设等差数列{an}的前n项和为Sn,若S15>0,S16<0,则数列的前15项中最大的项是( )
A.第1项 B.第8项 C.第9项 D.第15项
8.《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”;底面为矩形,一条侧棱垂直于底面的四棱锥称之为“阳马”,四个面均为直角三角形的四面体称为“鳖臑”,如图在堑堵中,,且.下列说法错误的是( )
A.四棱锥为“阳马”
B.四面体为“鳖臑”
C.四棱锥体积最大为
D.过A点分别作于点E,于点F,则
9.在△中,,,,,且点是的中点,则( )
A. B. C. D.
10.已知函数实数a,b满足不等式,则下列不等式成立的是( )
A. B. C. D.
11.已知函数,下列结论中正确的个数是( )
①的图象关于中心对称;②的图象关于对称;③的最大值为;④既是奇函数,又是周期函数.
A.1个 B.2个 C.3个 D.4个
12.用符号表示不超过的最大整数,例如:,,.设函数有三个零点,且,则的取值范围是( )
A. B.
C. D. QUOTE QUOTE
第Ⅱ卷(共 90 分)
二、填空题:本题共4小题,每小题5分,共20分.
13.已知轮船A和轮船B同时离开C岛,A船沿北偏东30°的方向航行,B船沿正北方向航行(如图).若A船的航行速度为40nmile/h,1h后,B船测得A船位于B船的北偏东45°的方向上,则此时A,B两船相距________nmile.
14.如图,在四棱锥中,四边形为矩形,,分别为和的中点,,则异面直线与所成角的余弦值为_____.
15.十九世纪丹麦数学家琴生对数学分析做出卓越贡献,特别是在函数的凹凸性与不等式方面留下了很多宝贵的成果,定义:函数f(x)在(a,b)上的导函数为,在(a,b)上的导函数为,若在(a,b)上<0恒成立,则称函数f(x)在(a,b)上为“严格凸函数”.若函数f(x)=在(1,4)上为“严格凸函数”,则m的取值范围为_____.
16.数列已知数列满足:,().正项数列满足:对于每个,,且,,成等比数列,则的前n项和为_____.
三、解答题:共70分,解答应写出文字说明 证明过程或演算步骤.第17-21为必考题,每个试题考生都必须作答,第22、23为选考题,考生根据要求作答.
(一)必做题:17-21,每题12分,共60分.
17. 已知的角A、B、C所对边分别为、、,,.
(1)求A;
(2)若角A的平分线与交于点,,求、.
18.如图1,在矩形ABCD中,AB= 4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1﹣ABCE,其中平面D1AE⊥平面ABCE.
(1)设F为CD1的中点,试在AB上找一点M,使得MF∥平面D1AE;
(2)求直线BD1与平面CD1E所成角的正弦值.
19.已知正项数列满足,,,成等比数列,.
(1)证明:数列是等比数列;
(2)求及数列的通项公式;
(3)若,求数列的前n项和
20.已知点在抛物线上,过点的直线与抛物线C有两个不同的交点A、B,且直线PA交轴于M,直线PB交轴于N.
(1)求直线的斜率的取值范围;
(2)设O为原点,,试判断是否为定值,若是,求值;若不是,求的取值范围.
21.已知函数,.
(1)当时,设,求证:;
(2)若恰有两个零点,求的最小整数值.
(二)选做题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
[选修4-4:坐标系与参数方程](10分)
22.在平面直角坐标系中,的参数方程为(为参数,),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,的极坐标方程为.
(1)求的直角坐标方程;
(2)与相交于不同两点、,线段中点为,点,若,求参数方程中的值.
[选修4-5:不等式选讲](10分)
23.已知函数.
(1)当时,求函数的最小值;
(2)若的解集为,且,求的最小值.
长春市重点高中2022届高三上学期12月第二学程考试
数学试卷答案
一、单选题
1.A 2.C 3.B 4.D 5.A 6.B 7.B 8.C 9.A 10.C 11.C12.B
二、填空题
13.【答案】 14.【答案】
15.【答案】 16.【答案】
3、解答题
17.(1)(2)
(1)由正弦定理及得,,
,即,所以,,
所以,,
,所以,.
(2)解:是角的平分线,,
,即,
,①,由(1)知,②
由①②解得.
18.【答案】(1)AM=;(2).
【详解】
(1)取D1E的中点N,连AN、NF,则,
∵,当AM=时,,
则且,则AMFN是平行四边形,AN∥MF.
又平面D1AE,平面D1AE,则MF∥平面D1AE.
(2)分别取AE、AB、BC的中点O、G、K,连OD1、OM、OK、EG,
∵AD1=ED1=2,∴OD1⊥AE,又平面D1AE⊥平面ABCE且交于AE,
∴OD1⊥平面ABCE.易知OK∥AB,OM∥EG∥BC,又AB⊥BC,∴OM⊥OK,
故如图建系O﹣xyz.
设平面CD1E的法向量 =(x, y, z),
∵EC∥y轴,∴,
∵,
∴D1为(0, 0,),又E为(﹣1, 1, 0),则,
由,取,则=(, 0, 1).
又B为(1, 3, 0),则,
记直线BD1与平面CD1E所成角的大小为,
则.
19.【答案】(1)证明见解析(2);(3);【分析】
小问1:由题意得,两边取对数可得,即可证明;
小问2:由(1)知,所以,即可求解;
小问3:由可化为,所以,结合小问2即可求证明.
(1)
因为,,成等比数列,所以,
所以因为,所以,
将式两边取对数,得,即,
所以,数列是首项为,公比为2的等比数列
(2)由(1)知,所以,所以
所以
(3)因为,即①;
又因为,所以,即②;
①式代入②式消去,可得
所以
因为,,则,所以
20.【答案】
(1)(3)定值为2
(1)
因点在抛物线上,则,解得,
所以抛物线C的方程为.
令直线的斜率为k,则直线方程为:,
由消去y并整理得:,
因直线与抛物线C有两个不同的交点A、B,则,解得且,
又直线PA,PB与相交,而点(1,-2)在抛物线C上,则直线不能过点(1,-2),
否则PA或PB之一平行于y轴,矛盾,因此,
综上得:,且,
所以直线的斜率的取值范围.
(2)设点,,,而,则,同理,
设,由(2)知,
直线方程:,即,则,
令,得,同理,
于是得
,
所以为定值2.
【点睛】方法点睛:求定值问题常见的方法有两种:(1)从特殊入手,求出定值,再证明这个值与变量无关;
(2)直接推理、计算,并在计算推理的过程中消去变量,从而得到定值.
21.【答案】(1)证明见解析;(2)2.
(1)当时,,
则,
因为, 所以,
所以,所以函数在上为增函数,
所以;
(2)当时,,设,
因为,所以,
所以,所以函数无零点,
当时,设, 因为,
所以, 即,
,
所以函数无零点
当时,,
设,,
所以函数在上为减函数,
又,,
所以在上存在零点,使,
当时,,当时,,
函数在上为增函数,在上为减函数,
因为,,
,
所以函数在,各一个零点,
综上所述:当时,恰有两个零点,当时,,
所以时,是恰有两个零点的最小整数值 .
22.【答案】(1)(2)或
(1)
解:由得,所以,
将代入得,即,
所以的直角坐标方程为;
(2)
解:将代入整理得
设、对应的参数分别为、,则、是方程的两根,
所以,因为,所以,所以,此时,
所以,所以,所以或.
23.【答案】(1)6 (2)【分析】
(1)解:当时,,所以,当时等号成立
∴函数的最小值为6.
(2)解:由得,
因为的解集为,∴,解得,∴,
(当且仅当时取等号),
(当且仅当时取等号),的最小值为.
同课章节目录
