2021-2022学年北师大版七年级数学下册2.2 探索直线平行的条件 同步练习卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学下册2.2 探索直线平行的条件 同步练习卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 199.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-06 20:47:42 | ||
图片预览



文档简介
2.2 探索直线平行的条件同步练习卷 2021-2022学年北师大版七年级数学下册
题号 一 二 三 总分
得分
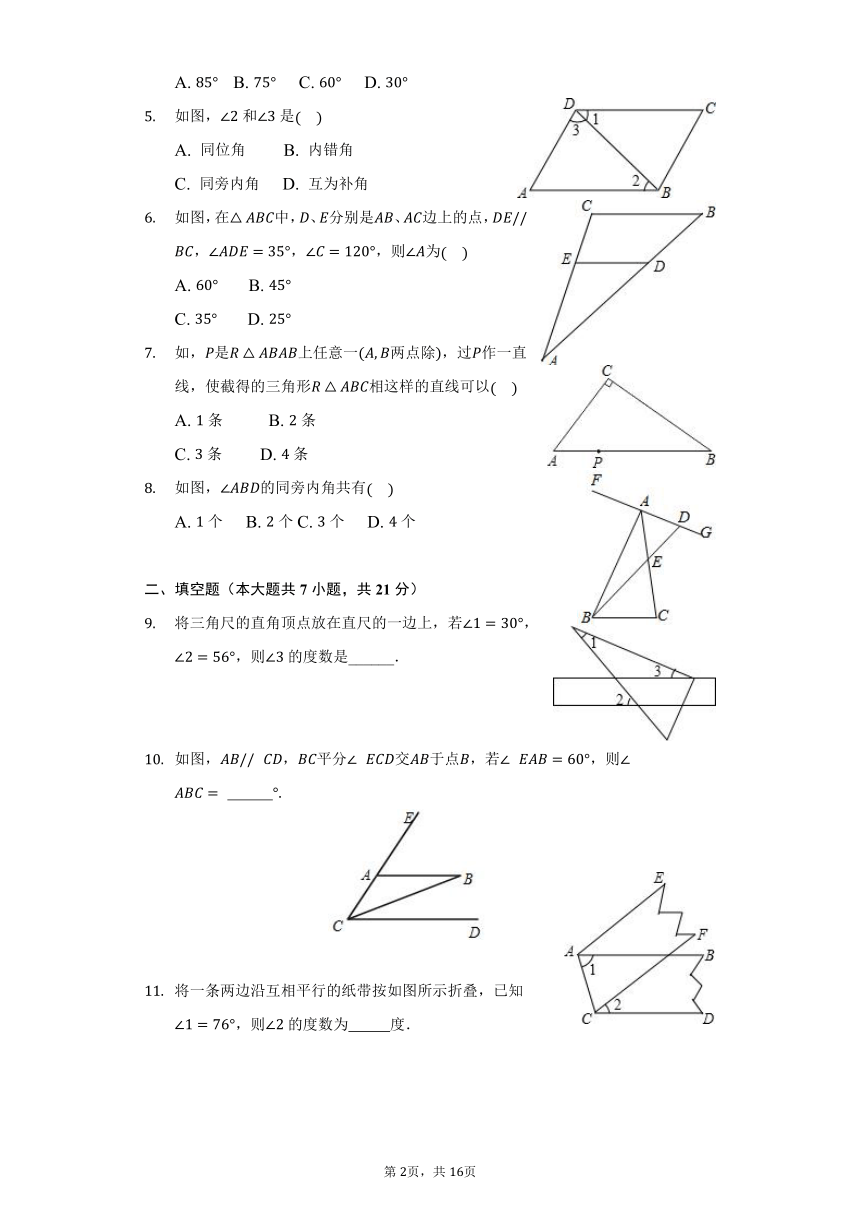
一、选择题(本大题共8小题,共24分)
下列说法中正确的是
A. 两条直线被第三条直线所截,同位角相等
B. 等角的补角相等
C. 两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行
D. 三条直线相交,必产生同位角、内错角、同旁内角
如图,下列说法正确的是
A. 若,可得
B. 若,可得
C. 若,可得
D. 若,可得
如图,下列判断中正确的个数是
与是同位角;
和是同旁内角;
和是内错角;
和是同位角.
A. 个 B. 个 C. 个 D. 个
如图,,点在线段上,若,则为
A. B. C. D.
如图,和是
A. 同位角 B. 内错角
C. 同旁内角 D. 互为补角
如图,在中,、分别是、边上的点,,,,则为
A. B.
C. D.
如,是上任意一两点除,过作一直线,使截得的三角形相这样的直线可以
A. 条 B. 条
C. 条 D. 条
如图,的同旁内角共有
A. 个 B. 个C. 个 D. 个
二、填空题(本大题共7小题,共21分)
将三角尺的直角顶点放在直尺的一边上,若,,则的度数是______.
如图, ,平分 交于点,若 ,则
将一条两边沿互相平行的纸带按如图所示折叠,已知,则的度数为 度.
下列说法:画两直线被第三条直线所截,同旁内角互补;垂直于同一条直线的两条直线互相平行;过一点有且只有一条直线与已知直线平行;平行于同一直线的两条直线互相平行.在图形的平移之后,对应点的连线段互相平行且相等.若的两边和的两边分别平行,且比的倍少,则的度数为或其中正确的是______.
如图所示,直线,被所截,填写下列两角的关系.
与是______ ;与是______ ;
与是______ ;与是______ .
光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,,则的度数为______ .
如图,直线、相交于点,,,那么的大小是______.
三、解答题(本大题共7小题,共75分)
如图所示,已知平分,平分,图中内错角有多少对?
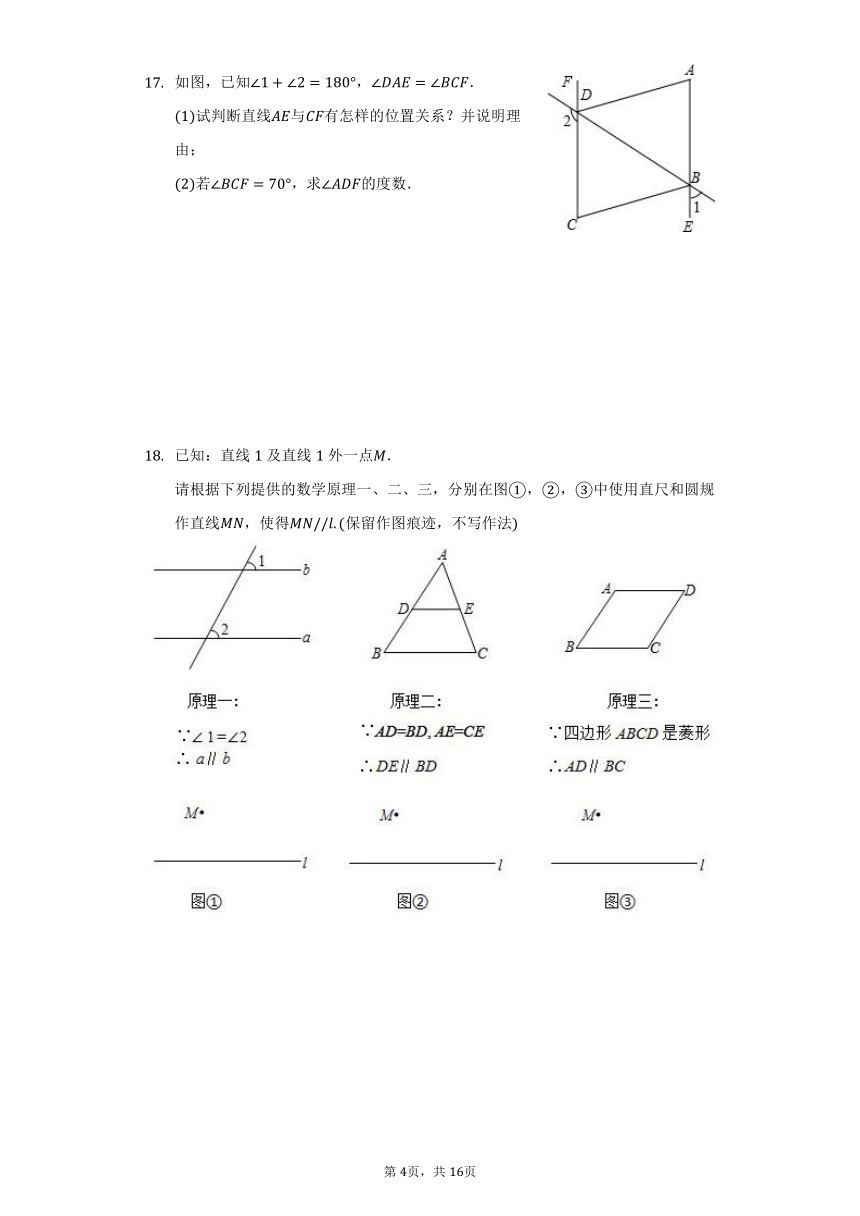
如图,已知,.
试判断直线与有怎样的位置关系?并说明理由;
若,求的度数.
已知:直线及直线外一点.
请根据下列提供的数学原理一、二、三,分别在图,,中使用直尺和圆规作直线,使得保留作图痕迹,不写作法
如图,
的同位角是 ,的内错角是 ;
若,则 ____________,根据是 ;
若,则 ____________,根据是 .
如图,,,,求的度数.
如图所示,已知,,求的度数.
解:
两直线平行,同位角相等
已知
.
如图,已知,,那么成立吗?为什么?下面是伊伊同学进行的推理,请你将伊伊同学的推理过程补充完整.
解:成立,理由如下:
已知,
______ 同旁内角互补,两直线平行,
______ ,
又因为已知,
______ ______ ,
______ ,
______
答案和解析
1.【答案】
【解析】解:、两条直线被第三条直线所截,同位角相等,说法错误,应该是平行时,同位角相等;
B、等角的补角相等,说法正确;
C、两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行,说法错误,应该是同旁内角互补,那么这两条直线平行;
D、三条直线相交,必产生同位角、内错角、同旁内角,说法错误,如果三条直线相交于一点.
故选:.
根据平行线的性质和平行线的判定可判断出、的正误,再根据余角的性质可判断出的正误;根据三线八角的定义可得的正误.
此题主要考查了平行线的判定与性质,以及余角性质,关键是熟练掌握课本定理.
2.【答案】
【解析】解:、由,不能得到,因为这两个角不是并不是由两条直线被第三条直线所截得到的,故A错误;
B、由,可得同位角相等,两直线平行,故B错误;
C、由,可得内错角相等,两直线平行,故C正确;
D、由,可得同位角相等,两直线平行,故D错误.
故选:.
由平行线的判定定理,逐个判断即可.
本题考查了平行线的判定定理,熟练掌握平行线判定定理、仔细推敲,认真思考是解题关键.
3.【答案】
【解析】解:与是同位角,正确;
与是同旁内角.正确;
与是内错角,正确;
与不是同位角,错误.
故选:.
准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
此题主要考查了三线八角,在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
4.【答案】
【解析】解:,
,
又,
,
,即,
.
故选:.
先由,得,,得,再根据三角形内角和定理得,,即,从而求出.
此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出,再由得出,由三角形内角和定理求出.
5.【答案】
【解析】解:和是和被所截得到的同旁内角,
故选C.
根据同位角、内错角、同旁内角的定义解答.
本题考查了同位角、内错角、同旁内角,熟悉它们的定义是解题的关键.
6.【答案】
【解析】解:,,
,
,,
.
故选:.
先根据平行线的性质得出,再由三角形内角和定理即可求出的度数即可.
本题考查的是平行线的性质,解答此类题目时往往用到三角形的内角和是这一隐含条件.
7.【答案】
【解析】解:过点可作或,可相三角形;
;
所以有条.
故选:
本根据相似角形的判定法进行求解.
此题考查了相似形的定:
有个对应边的比相等且其角等,则两三角形相似;
三组应边的比相则两三角形相似.
8.【答案】
【解析】解:与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
故选:.
根据同旁内角的定义,结合图形进行判断即可.
本题考查同旁内角,理解同旁内角的定义是正确判断的前提.
9.【答案】
【解析】解:如图,
,
,
又,
.
故答案为:.
如图,由平行线的性质可求得,结合三角形外角的性质可求得.
本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,,.
10.【答案】
【解析】本题考察了学生对同位角,内错角的理解,同位角是在截线两旁,在被截两直线的同方向,并且同位角通常是成对出现的而两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫内错角.
解:与是同位角,
,
又两平行线之间内错角相等,
,
又平分,,
故填.
11.【答案】
【解析】试题分析:先找出与的关系,再根据平行线性质求出,之后可得.
根据题意,;
,
;
故应填.
12.【答案】
【解析】
【分析】
本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行或共线且相等.也考查了平行线的性质.
根据平行线的性质对进行判断;由于掉了条件,导致其错误;利用平行公理对进行判断;利用平行线的传递性对进行判断;利用平移的性质对进行判断;利用两个角的两边分别平行,则两个角相等或互补,通过方程的思想可求出的度数,从而对进行判断.
【解答】
解:画两平行直线被第三条直线所截,同旁内角互补,所以错误;
在同一平面内,垂直于同一条直线的两条直线互相平行;所以错误;
过直线外一点有且只有一条直线与已知直线平行;所以错误;
平行于同一直线的两条直线互相平行.所以正确;
在图形的平移之后,对应点的连线段互相平行或共线且相等,所以错误;
若的两边和的两边分别平行,则与相等或互补,由于比的倍少,所以的度数为或所以正确.
故答案为.
13.【答案】对顶角;同旁内角;内错角;同位角
【解析】解:与是对顶角;
与是同旁内角;
与是内错角;
与是同位角.
故答案为:对顶角;同旁内角;内错角;同位角.
根据对顶角、同位角、内错角、同旁内角的定义分析可得答案.
此题主要考查了三线八角,关键是掌握在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
14.【答案】
【解析】解:如图,,
,
,
,
,
,
,
,
.
故答案为:.
光在水中是平行的光线,在空气中也是平行的,依据平行线的性质进行判断,即可得出图中的度数.
本题主要考查了平行线的性质,解题时注意:两直线平行时,同位角相等,内错角相等,同旁内角互补.
15.【答案】.
【解析】解:,
.
,
.
故答案为:.
依据垂线的定义可求得,然后依据对顶角的性质可求得的度数,最后依据求解即可.
本题主要考查的是对顶角的性质和垂线的定义,掌握对顶角的性质和垂线的定义是解题的关键.
16.【答案】解:图中的内错角有:与,与,与,与共对.
【解析】内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的两旁,则这样一对角叫做内错角.
本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.
17.【答案】解:,
理由是:,,
,
同位角相等,两直线平行;
,
,
又,
,
,
.
【解析】求出,根据平行线的判定推出即可;
根据平行线的性质得出,求出,根据平行线的判定推出,根据平行线的性质得出即可.
本题考查了平行线的性质和判定的应用,注意:两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.
18.【答案】解:如图所示,
根据题意的数学原理一、二、三,
图,,中直线即为所求.
【解析】根据题意提供的数学原理一、二、三,分别在图,,中使用直尺和圆规作直线,使得即可.
本题考查了作图复杂作图,解决本题的关键是掌握平行线的判定、菱形的性质.
19.【答案】内错角相等,两直线平行同位角相等,两直线平行
【解析】试题分析:根据同位角,内错角定义得出即可,根据平行线的判定推出即可.
的同位角是,的内错角是,
,
内错角相等,两直线平行,
,
同位角相等,两直线平行,
故答案为:,,,,内错角相等,两直线平行,,,同位角相等,两直线平行,
20.【答案】解:因为,
所以,
又因为,
所以,
所以,
所以.
【解析】由平行线的性质可得,又由条件可判定,可得到,可求得答案.
本题主要考查平行线的性质和判定,掌握两直线平行同位角相等、两直线平行内错角相等是解题的关键.
21.【答案】解:已知
同位角相等,两直线平行
两直线平行,同位角相等
已知
.
故答案为:已知;同位角相等,两直线平行;;
【解析】试题分析:由已知角相等,利用同位角相等两直线平行得到与平行,再利用两直线平行同位角相等得到,由的度数即可求出的度数.
22.【答案】 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 两直线平行,内错角相等
【解析】解:成立,理由如下:
已知,
同旁内角互补,两直线平行,
两直线平行,同位角相等,
又因为已知,
等量代换,
内错角相等,两直线平行,
两直线平行,内错角相等.
故答案为:,两直线平行,同位角相等,,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
根据平行线的判定与性质即可说明理由.
本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
第6页,共16页
题号 一 二 三 总分
得分
一、选择题(本大题共8小题,共24分)
下列说法中正确的是
A. 两条直线被第三条直线所截,同位角相等
B. 等角的补角相等
C. 两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行
D. 三条直线相交,必产生同位角、内错角、同旁内角
如图,下列说法正确的是
A. 若,可得
B. 若,可得
C. 若,可得
D. 若,可得
如图,下列判断中正确的个数是
与是同位角;
和是同旁内角;
和是内错角;
和是同位角.
A. 个 B. 个 C. 个 D. 个
如图,,点在线段上,若,则为
A. B. C. D.
如图,和是
A. 同位角 B. 内错角
C. 同旁内角 D. 互为补角
如图,在中,、分别是、边上的点,,,,则为
A. B.
C. D.
如,是上任意一两点除,过作一直线,使截得的三角形相这样的直线可以
A. 条 B. 条
C. 条 D. 条
如图,的同旁内角共有
A. 个 B. 个C. 个 D. 个
二、填空题(本大题共7小题,共21分)
将三角尺的直角顶点放在直尺的一边上,若,,则的度数是______.
如图, ,平分 交于点,若 ,则
将一条两边沿互相平行的纸带按如图所示折叠,已知,则的度数为 度.
下列说法:画两直线被第三条直线所截,同旁内角互补;垂直于同一条直线的两条直线互相平行;过一点有且只有一条直线与已知直线平行;平行于同一直线的两条直线互相平行.在图形的平移之后,对应点的连线段互相平行且相等.若的两边和的两边分别平行,且比的倍少,则的度数为或其中正确的是______.
如图所示,直线,被所截,填写下列两角的关系.
与是______ ;与是______ ;
与是______ ;与是______ .
光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中是平行的光线,在空气中也是平行的,如图,,则的度数为______ .
如图,直线、相交于点,,,那么的大小是______.
三、解答题(本大题共7小题,共75分)
如图所示,已知平分,平分,图中内错角有多少对?
如图,已知,.
试判断直线与有怎样的位置关系?并说明理由;
若,求的度数.
已知:直线及直线外一点.
请根据下列提供的数学原理一、二、三,分别在图,,中使用直尺和圆规作直线,使得保留作图痕迹,不写作法
如图,
的同位角是 ,的内错角是 ;
若,则 ____________,根据是 ;
若,则 ____________,根据是 .
如图,,,,求的度数.
如图所示,已知,,求的度数.
解:
两直线平行,同位角相等
已知
.
如图,已知,,那么成立吗?为什么?下面是伊伊同学进行的推理,请你将伊伊同学的推理过程补充完整.
解:成立,理由如下:
已知,
______ 同旁内角互补,两直线平行,
______ ,
又因为已知,
______ ______ ,
______ ,
______
答案和解析
1.【答案】
【解析】解:、两条直线被第三条直线所截,同位角相等,说法错误,应该是平行时,同位角相等;
B、等角的补角相等,说法正确;
C、两条直线被第三条直线所截,如果同旁内角相等,那么这两条直线平行,说法错误,应该是同旁内角互补,那么这两条直线平行;
D、三条直线相交,必产生同位角、内错角、同旁内角,说法错误,如果三条直线相交于一点.
故选:.
根据平行线的性质和平行线的判定可判断出、的正误,再根据余角的性质可判断出的正误;根据三线八角的定义可得的正误.
此题主要考查了平行线的判定与性质,以及余角性质,关键是熟练掌握课本定理.
2.【答案】
【解析】解:、由,不能得到,因为这两个角不是并不是由两条直线被第三条直线所截得到的,故A错误;
B、由,可得同位角相等,两直线平行,故B错误;
C、由,可得内错角相等,两直线平行,故C正确;
D、由,可得同位角相等,两直线平行,故D错误.
故选:.
由平行线的判定定理,逐个判断即可.
本题考查了平行线的判定定理,熟练掌握平行线判定定理、仔细推敲,认真思考是解题关键.
3.【答案】
【解析】解:与是同位角,正确;
与是同旁内角.正确;
与是内错角,正确;
与不是同位角,错误.
故选:.
准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.
此题主要考查了三线八角,在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系.
4.【答案】
【解析】解:,
,
又,
,
,即,
.
故选:.
先由,得,,得,再根据三角形内角和定理得,,即,从而求出.
此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出,再由得出,由三角形内角和定理求出.
5.【答案】
【解析】解:和是和被所截得到的同旁内角,
故选C.
根据同位角、内错角、同旁内角的定义解答.
本题考查了同位角、内错角、同旁内角,熟悉它们的定义是解题的关键.
6.【答案】
【解析】解:,,
,
,,
.
故选:.
先根据平行线的性质得出,再由三角形内角和定理即可求出的度数即可.
本题考查的是平行线的性质,解答此类题目时往往用到三角形的内角和是这一隐含条件.
7.【答案】
【解析】解:过点可作或,可相三角形;
;
所以有条.
故选:
本根据相似角形的判定法进行求解.
此题考查了相似形的定:
有个对应边的比相等且其角等,则两三角形相似;
三组应边的比相则两三角形相似.
8.【答案】
【解析】解:与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
与是直线、,被直线所截而成的同旁内角,
故选:.
根据同旁内角的定义,结合图形进行判断即可.
本题考查同旁内角,理解同旁内角的定义是正确判断的前提.
9.【答案】
【解析】解:如图,
,
,
又,
.
故答案为:.
如图,由平行线的性质可求得,结合三角形外角的性质可求得.
本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,,.
10.【答案】
【解析】本题考察了学生对同位角,内错角的理解,同位角是在截线两旁,在被截两直线的同方向,并且同位角通常是成对出现的而两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫内错角.
解:与是同位角,
,
又两平行线之间内错角相等,
,
又平分,,
故填.
11.【答案】
【解析】试题分析:先找出与的关系,再根据平行线性质求出,之后可得.
根据题意,;
,
;
故应填.
12.【答案】
【解析】
【分析】
本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行或共线且相等.也考查了平行线的性质.
根据平行线的性质对进行判断;由于掉了条件,导致其错误;利用平行公理对进行判断;利用平行线的传递性对进行判断;利用平移的性质对进行判断;利用两个角的两边分别平行,则两个角相等或互补,通过方程的思想可求出的度数,从而对进行判断.
【解答】
解:画两平行直线被第三条直线所截,同旁内角互补,所以错误;
在同一平面内,垂直于同一条直线的两条直线互相平行;所以错误;
过直线外一点有且只有一条直线与已知直线平行;所以错误;
平行于同一直线的两条直线互相平行.所以正确;
在图形的平移之后,对应点的连线段互相平行或共线且相等,所以错误;
若的两边和的两边分别平行,则与相等或互补,由于比的倍少,所以的度数为或所以正确.
故答案为.
13.【答案】对顶角;同旁内角;内错角;同位角
【解析】解:与是对顶角;
与是同旁内角;
与是内错角;
与是同位角.
故答案为:对顶角;同旁内角;内错角;同位角.
根据对顶角、同位角、内错角、同旁内角的定义分析可得答案.
此题主要考查了三线八角,关键是掌握在复杂的图形中判别三类角时,应从角的两边入手,具有上述关系的角必有两边在同一直线上,此直线即为截线,而另外不在同一直线上的两边,它们所在的直线即为被截的线.同位角的边构成““形,内错角的边构成““形,同旁内角的边构成“”形.
14.【答案】
【解析】解:如图,,
,
,
,
,
,
,
,
.
故答案为:.
光在水中是平行的光线,在空气中也是平行的,依据平行线的性质进行判断,即可得出图中的度数.
本题主要考查了平行线的性质,解题时注意:两直线平行时,同位角相等,内错角相等,同旁内角互补.
15.【答案】.
【解析】解:,
.
,
.
故答案为:.
依据垂线的定义可求得,然后依据对顶角的性质可求得的度数,最后依据求解即可.
本题主要考查的是对顶角的性质和垂线的定义,掌握对顶角的性质和垂线的定义是解题的关键.
16.【答案】解:图中的内错角有:与,与,与,与共对.
【解析】内错角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线截线的两旁,则这样一对角叫做内错角.
本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.
17.【答案】解:,
理由是:,,
,
同位角相等,两直线平行;
,
,
又,
,
,
.
【解析】求出,根据平行线的判定推出即可;
根据平行线的性质得出,求出,根据平行线的判定推出,根据平行线的性质得出即可.
本题考查了平行线的性质和判定的应用,注意:两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.
18.【答案】解:如图所示,
根据题意的数学原理一、二、三,
图,,中直线即为所求.
【解析】根据题意提供的数学原理一、二、三,分别在图,,中使用直尺和圆规作直线,使得即可.
本题考查了作图复杂作图,解决本题的关键是掌握平行线的判定、菱形的性质.
19.【答案】内错角相等,两直线平行同位角相等,两直线平行
【解析】试题分析:根据同位角,内错角定义得出即可,根据平行线的判定推出即可.
的同位角是,的内错角是,
,
内错角相等,两直线平行,
,
同位角相等,两直线平行,
故答案为:,,,,内错角相等,两直线平行,,,同位角相等,两直线平行,
20.【答案】解:因为,
所以,
又因为,
所以,
所以,
所以.
【解析】由平行线的性质可得,又由条件可判定,可得到,可求得答案.
本题主要考查平行线的性质和判定,掌握两直线平行同位角相等、两直线平行内错角相等是解题的关键.
21.【答案】解:已知
同位角相等,两直线平行
两直线平行,同位角相等
已知
.
故答案为:已知;同位角相等,两直线平行;;
【解析】试题分析:由已知角相等,利用同位角相等两直线平行得到与平行,再利用两直线平行同位角相等得到,由的度数即可求出的度数.
22.【答案】 两直线平行,同位角相等 等量代换 内错角相等,两直线平行 两直线平行,内错角相等
【解析】解:成立,理由如下:
已知,
同旁内角互补,两直线平行,
两直线平行,同位角相等,
又因为已知,
等量代换,
内错角相等,两直线平行,
两直线平行,内错角相等.
故答案为:,两直线平行,同位角相等,,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
根据平行线的判定与性质即可说明理由.
本题考查了平行线的判定与性质,解决本题的关键是掌握平行线的判定与性质.
第6页,共16页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
