2021-2022学年人教版数学七年级下册8.3实际问题与二元一次方程组同步训练 (word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册8.3实际问题与二元一次方程组同步训练 (word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 130.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 08:44:15 | ||
图片预览




文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
测试时间:30分钟
一、选择题
1.(2021河北保定顺平期末)小明和小丽同时到一家水果店买水果,小明买1 kg荔枝和5 kg西瓜,共花了30元;小丽买2 kg荔枝和3 kg西瓜,共花了46元,设荔枝每千克x元,西瓜每千克y元,根据题意,列出方程组应为( )
A. B.
C. D.
2.(2021辽宁葫芦岛绥中期末)为了丰富学生的课外小组活动,学生手工社团准备将长为5 m的彩绳,截成1 m或2 m长的彩绳,用来做手工编织,在不造成浪费的前提下,不同的截法有( )
A.2种 B.3种 C.4种 D.5种
3.(2021重庆实验外国语学校期末)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大、小齿轮刚好配套 设安排x名工人加工大齿轮,安排y名工人加工小齿轮,可列方程组为( )
A. B.
C. D.
4.(2021贵州遵义期末)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何 ”译文:“现有一根木头,不知道它的长短.用一根绳子去量木头,绳子比木头长4.5尺;将绳子对折后去量,则绳子比木头短1尺.问木头的长度是多少尺 ”设木长x尺、绳子长y尺,可列方程组为( )
A. B.
C. D.
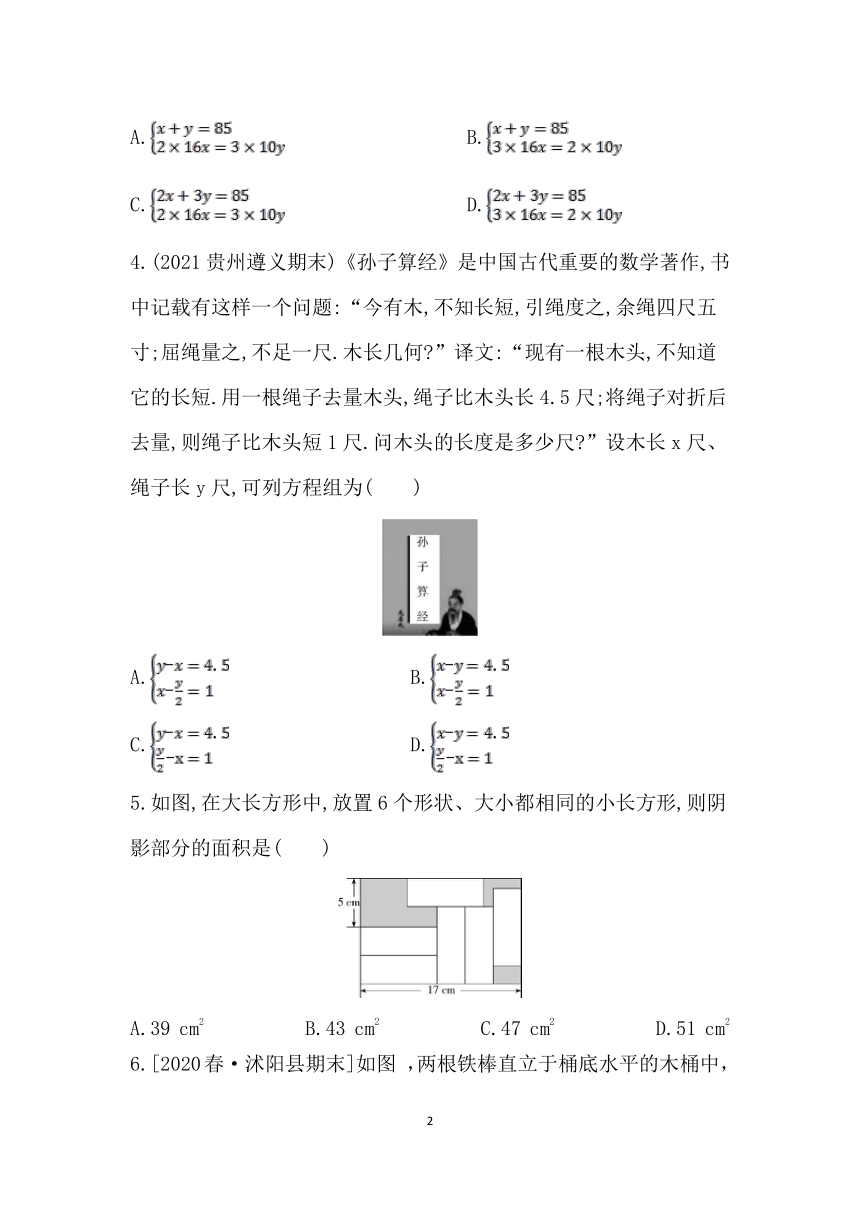
5.如图,在大长方形中,放置6个形状、大小都相同的小长方形,则阴影部分的面积是( )
A.39 cm2 B.43 cm2 C.47 cm2 D.51 cm2
6.[2020春·沭阳县期末]如图 ,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为110 cm,此时木桶中水的深度是( )
A.60 cm B.50 cm
C.40 cm D.30 cm
7.从巴中到广元的路程全长约为126 km.一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45 min相遇,相遇时小汽车比货车多行6 km.设小汽车和货车的速度分别为x km/h,y km/h,则下列方程组正确的是( )
A. B.
C. D.
二、填空题
8.(2021河北秦皇岛青龙期末)已知甲数的2倍与乙数的3倍之和是12,甲数的3倍与乙数的2倍之差是5,求这两个数.若设甲数为x,乙数为y,根据题中的等量关系,列出的方程组为 .
9.(2021浙江宁波北仑期末)小慧去花店买鲜花,若买6支玫瑰和4支百合,则她所带的钱还剩下11元;若买4支玫瑰和6支百合,则她所带的钱还缺5元.若只买10支玫瑰,则她所带的钱还剩下 元.
10.(2021重庆丰都期末)如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30 cm,两块竖放的墙砖比两块横放的墙砖高50 cm,则每块墙砖的截面面积是 cm2.
11.一个两位数,个位数字与十位数字之和为6.若其中间加一个0,与原数的和为228,则原数为多少?若设十位数字为x,个位数字为y,则可列方程组为________________.
三、解答题
12.(2021河北保定顺平期末)新冠肺炎疫情在全球蔓延,接种新冠疫苗是当前抗击疫情最有效的手段.我县注射的疫苗有两种,一种是2针剂的灭活疫苗,另一种是3针剂的重组蛋白疫苗.某校120名教职工全部完成其中一种疫苗的注射,共注射了325针.注射2针剂和3针剂疫苗的教职工各有多少人
13.(2021河北保定定州期末)小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件和第一个方程,并求解这道应用题.
应用题:小东在某商场看中的一台电视和一台空调在“五一”前共需要5 500元,由于该商场开展“五一”促销活动,同样的电视打八折销售,于是小东在促销期间购买了同样的电视一台,空调两台,共花费7 200元,求“五一”前同样的电视和空调每台各多少元.
解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得
被墨水污染的条件是 .
被墨水污染的第一个方程是 .
14.小丽在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中,前两次购买时,A,B两种商品都未打折,第三次购买时,A,B两种商品同时打折,三次购买A,B两种商品的数量和费用如下表所示:
次数 购买A商品的数量/个 购买B商品的数量/个 购买总费用/元
第一次 6 5 980
第二次 3 7 940
第三次 9 8 912
(1)求A,B两种商品的售价;
(2)若第三次购买时,A,B两种商品的折扣相同,则商店是打几折出售这两种商品的
(3)在(2)的条件下,若小丽第四次购物共花去了480元,则小丽有哪几种购买方案
15.明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多入住3人,一次性定客房25间以上(含25间),房费按八折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
一、选择题
1.答案 A ∵小明买1 kg荔枝和5 kg西瓜,共花了30元,
∴x+5y=30;
∵小丽买2 kg荔枝和3 kg西瓜,共花了46元,
∴2x+3y=46.
联立两方程组成方程组得故选A.
2.答案 B 设可以截成1 m长的彩绳x根,2 m长的彩绳y根,
依题意得x+2y=5,∴x=5-2y.
∵x,y均为非负整数,
∴或或
∴共有3种不同的截法.
故选B.
3.答案 B 根据机械厂加工车间有85名工人且加工的大、小齿轮刚好配套,即可得出关于x,y的二元一次方程组:故选B.
4.答案 A 由绳子比木头长4.5尺得y-x=4.5;
由绳子对折后比木头短1尺得x-=1,
组成方程组,即得故选A.
5.答案 B 设每个小长方形的长为x cm,宽为y cm,
根据图中给定各边之间的关系,可得
解得∴阴影部分的面积为17×(2×3+5)-6×8×3=43(cm2).故选B.
6.答案 C
7.答案 D
二、填空题
8.答案
解析 由甲数的2倍与乙数的3倍之和是12,可得2x+3y=12,
由甲数的3倍与乙数的2倍之差是5,可得3x-2y=5,
故可列方程组为
故答案为
9.答案 43
解析 设每支玫瑰的价格为x元,每支百合的价格为y元,
依题意得6x+4y+11=4x+6y-5,
∴y=x+8,
∴6x+4y+11-10x=6x+4(x+8)+11-10x=43.故答案为43.
10.答案 900
解析 设每块墙砖截面的长为x cm,宽为y cm,
依题意得
解得
∴每块墙砖的截面面积是45×20=900(cm2).故答案为900.
11. 答案
三、解答题
12.解析 设注射2针剂疫苗的教职工有x人,注射3针剂疫苗的教职工有y人,
依题意得
解得
答:注射2针剂疫苗的教职工有35人,注射3针剂疫苗的教职工有85人.
13.解析 ∵“五一”前同样的电视每台x元,空调每台y元,方程②为0.8x+2(y-400)=7 200,
∴y-400表示每台空调在“五一”促销活动中的售价,
∴被墨水污染的条件是同样的空调每台降价400元.
∵小东在某商场看中的一台电视和一台空调在“五一”前共需要5 500元,
∴被墨水污染的第一个方程是x+y=5 500.
故答案为同样的空调每台降价400元;x+y=5 500.
14.解析 (1)设A商品的售价为x元/个,B商品的售价为y元/个,
依题意得
解得
答:A商品的售价为80元/个,B商品的售价为100元/个.
(2)设商店是打a折出售这两种商品的,
依题意得(80×9+100×8)×=912,
解得a=6.
答:商店是打六折出售这两种商品的.
(3)设购买A商品m个,B商品n个,
依题意得80×0.6m+100×0.6n=480,
∴m=10-n.
又∵m,n均为正整数,
∴
答:小丽只有一种购买方案,购买5个A商品,4个B商品.
15.解析(1)该店有客房8间,房客63人.
(2)诗中“众客”再次一起入住,他们应选择一次性订房25间更合算.
1
班级 姓名
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
测试时间:30分钟
一、选择题
1.(2021河北保定顺平期末)小明和小丽同时到一家水果店买水果,小明买1 kg荔枝和5 kg西瓜,共花了30元;小丽买2 kg荔枝和3 kg西瓜,共花了46元,设荔枝每千克x元,西瓜每千克y元,根据题意,列出方程组应为( )
A. B.
C. D.
2.(2021辽宁葫芦岛绥中期末)为了丰富学生的课外小组活动,学生手工社团准备将长为5 m的彩绳,截成1 m或2 m长的彩绳,用来做手工编织,在不造成浪费的前提下,不同的截法有( )
A.2种 B.3种 C.4种 D.5种
3.(2021重庆实验外国语学校期末)机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,已知2个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大、小齿轮刚好配套 设安排x名工人加工大齿轮,安排y名工人加工小齿轮,可列方程组为( )
A. B.
C. D.
4.(2021贵州遵义期末)《孙子算经》是中国古代重要的数学著作,书中记载有这样一个问题:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何 ”译文:“现有一根木头,不知道它的长短.用一根绳子去量木头,绳子比木头长4.5尺;将绳子对折后去量,则绳子比木头短1尺.问木头的长度是多少尺 ”设木长x尺、绳子长y尺,可列方程组为( )
A. B.
C. D.
5.如图,在大长方形中,放置6个形状、大小都相同的小长方形,则阴影部分的面积是( )
A.39 cm2 B.43 cm2 C.47 cm2 D.51 cm2
6.[2020春·沭阳县期末]如图 ,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的.两根铁棒长度之和为110 cm,此时木桶中水的深度是( )
A.60 cm B.50 cm
C.40 cm D.30 cm
7.从巴中到广元的路程全长约为126 km.一辆小汽车、一辆货车同时从巴中、广元两地相向开出,经过45 min相遇,相遇时小汽车比货车多行6 km.设小汽车和货车的速度分别为x km/h,y km/h,则下列方程组正确的是( )
A. B.
C. D.
二、填空题
8.(2021河北秦皇岛青龙期末)已知甲数的2倍与乙数的3倍之和是12,甲数的3倍与乙数的2倍之差是5,求这两个数.若设甲数为x,乙数为y,根据题中的等量关系,列出的方程组为 .
9.(2021浙江宁波北仑期末)小慧去花店买鲜花,若买6支玫瑰和4支百合,则她所带的钱还剩下11元;若买4支玫瑰和6支百合,则她所带的钱还缺5元.若只买10支玫瑰,则她所带的钱还剩下 元.
10.(2021重庆丰都期末)如图所示是由截面为同一种矩形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低30 cm,两块竖放的墙砖比两块横放的墙砖高50 cm,则每块墙砖的截面面积是 cm2.
11.一个两位数,个位数字与十位数字之和为6.若其中间加一个0,与原数的和为228,则原数为多少?若设十位数字为x,个位数字为y,则可列方程组为________________.
三、解答题
12.(2021河北保定顺平期末)新冠肺炎疫情在全球蔓延,接种新冠疫苗是当前抗击疫情最有效的手段.我县注射的疫苗有两种,一种是2针剂的灭活疫苗,另一种是3针剂的重组蛋白疫苗.某校120名教职工全部完成其中一种疫苗的注射,共注射了325针.注射2针剂和3针剂疫苗的教职工各有多少人
13.(2021河北保定定州期末)小明作业本中有一页被墨水污染了,已知他所列的方程组是正确的,写出题中被墨水污染的条件和第一个方程,并求解这道应用题.
应用题:小东在某商场看中的一台电视和一台空调在“五一”前共需要5 500元,由于该商场开展“五一”促销活动,同样的电视打八折销售,于是小东在促销期间购买了同样的电视一台,空调两台,共花费7 200元,求“五一”前同样的电视和空调每台各多少元.
解:设“五一”前同样的电视每台x元,空调每台y元,根据题意,得
被墨水污染的条件是 .
被墨水污染的第一个方程是 .
14.小丽在某商店购买A,B两种商品若干次(每次A,B两种商品都购买),其中,前两次购买时,A,B两种商品都未打折,第三次购买时,A,B两种商品同时打折,三次购买A,B两种商品的数量和费用如下表所示:
次数 购买A商品的数量/个 购买B商品的数量/个 购买总费用/元
第一次 6 5 980
第二次 3 7 940
第三次 9 8 912
(1)求A,B两种商品的售价;
(2)若第三次购买时,A,B两种商品的折扣相同,则商店是打几折出售这两种商品的
(3)在(2)的条件下,若小丽第四次购物共花去了480元,则小丽有哪几种购买方案
15.明代数学家程大位所著的《算法统宗》全称《直指算法统宗》,是中国古代数学名著.某数学兴趣小组发现《算法统宗》里有这样一首诗:我问开店李三公,众客都来到店中,一房七客多七客,一房九客一房空.诗中后两句的意思是:如果每一间客房住7人,那么有7人无房可住;如果每一间客房住9人,那么就空出一间房.
(1)该店有客房多少间?房客多少人?
(2)假设店主李三公将客房进行改造后,共有50间客房.每间客房收费30钱,且每间客房最多入住3人,一次性定客房25间以上(含25间),房费按八折优惠.若诗中“众客”再次一起入住,他们如何订房更合算?
一、选择题
1.答案 A ∵小明买1 kg荔枝和5 kg西瓜,共花了30元,
∴x+5y=30;
∵小丽买2 kg荔枝和3 kg西瓜,共花了46元,
∴2x+3y=46.
联立两方程组成方程组得故选A.
2.答案 B 设可以截成1 m长的彩绳x根,2 m长的彩绳y根,
依题意得x+2y=5,∴x=5-2y.
∵x,y均为非负整数,
∴或或
∴共有3种不同的截法.
故选B.
3.答案 B 根据机械厂加工车间有85名工人且加工的大、小齿轮刚好配套,即可得出关于x,y的二元一次方程组:故选B.
4.答案 A 由绳子比木头长4.5尺得y-x=4.5;
由绳子对折后比木头短1尺得x-=1,
组成方程组,即得故选A.
5.答案 B 设每个小长方形的长为x cm,宽为y cm,
根据图中给定各边之间的关系,可得
解得∴阴影部分的面积为17×(2×3+5)-6×8×3=43(cm2).故选B.
6.答案 C
7.答案 D
二、填空题
8.答案
解析 由甲数的2倍与乙数的3倍之和是12,可得2x+3y=12,
由甲数的3倍与乙数的2倍之差是5,可得3x-2y=5,
故可列方程组为
故答案为
9.答案 43
解析 设每支玫瑰的价格为x元,每支百合的价格为y元,
依题意得6x+4y+11=4x+6y-5,
∴y=x+8,
∴6x+4y+11-10x=6x+4(x+8)+11-10x=43.故答案为43.
10.答案 900
解析 设每块墙砖截面的长为x cm,宽为y cm,
依题意得
解得
∴每块墙砖的截面面积是45×20=900(cm2).故答案为900.
11. 答案
三、解答题
12.解析 设注射2针剂疫苗的教职工有x人,注射3针剂疫苗的教职工有y人,
依题意得
解得
答:注射2针剂疫苗的教职工有35人,注射3针剂疫苗的教职工有85人.
13.解析 ∵“五一”前同样的电视每台x元,空调每台y元,方程②为0.8x+2(y-400)=7 200,
∴y-400表示每台空调在“五一”促销活动中的售价,
∴被墨水污染的条件是同样的空调每台降价400元.
∵小东在某商场看中的一台电视和一台空调在“五一”前共需要5 500元,
∴被墨水污染的第一个方程是x+y=5 500.
故答案为同样的空调每台降价400元;x+y=5 500.
14.解析 (1)设A商品的售价为x元/个,B商品的售价为y元/个,
依题意得
解得
答:A商品的售价为80元/个,B商品的售价为100元/个.
(2)设商店是打a折出售这两种商品的,
依题意得(80×9+100×8)×=912,
解得a=6.
答:商店是打六折出售这两种商品的.
(3)设购买A商品m个,B商品n个,
依题意得80×0.6m+100×0.6n=480,
∴m=10-n.
又∵m,n均为正整数,
∴
答:小丽只有一种购买方案,购买5个A商品,4个B商品.
15.解析(1)该店有客房8间,房客63人.
(2)诗中“众客”再次一起入住,他们应选择一次性订房25间更合算.
1
