2021-2022学年人教版数学七年级下册8.4三元一次方程组的解法同步训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册8.4三元一次方程组的解法同步训练(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 121.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 08:45:44 | ||
图片预览



文档简介
2022年春人教版初中七年级数学下册 同步训练
班级 姓名
第八章 二元一次方程组
8.4 三元一次方程组的解法
测试时间:20分钟
一、选择题
1.(2021湖南长沙开福期中)观察方程组的系数特征,若要使求解简便,消元的方法应选取( )
A.先消去x B.先消去y
C.先消去z D.以上说法都不对
2.(2021河北秦皇岛青龙期末)三元一次方程组的解是( )
A. B. C. D.
3.某天,小李在某电商平台上选择了甲、乙、丙三种商品,当购物车内选3件甲,2件乙,1件丙时显示价格为420元;当选2件甲,3件乙,4件丙时显示价格为580元,那么购买甲、乙、丙各一件时应该付款( )
A.580元 B.500元 C.420元 D.200元
4. 利用加减消元法解方程组下列做法正确的是( )
A.要消去z,先将①+②,再将①×2+③
B.要消去z,先将①+②,再将①×3-③
C.要消去y,先将①-③×2,再将②-③
D.要消去y,先将①-②×2,再将②+③
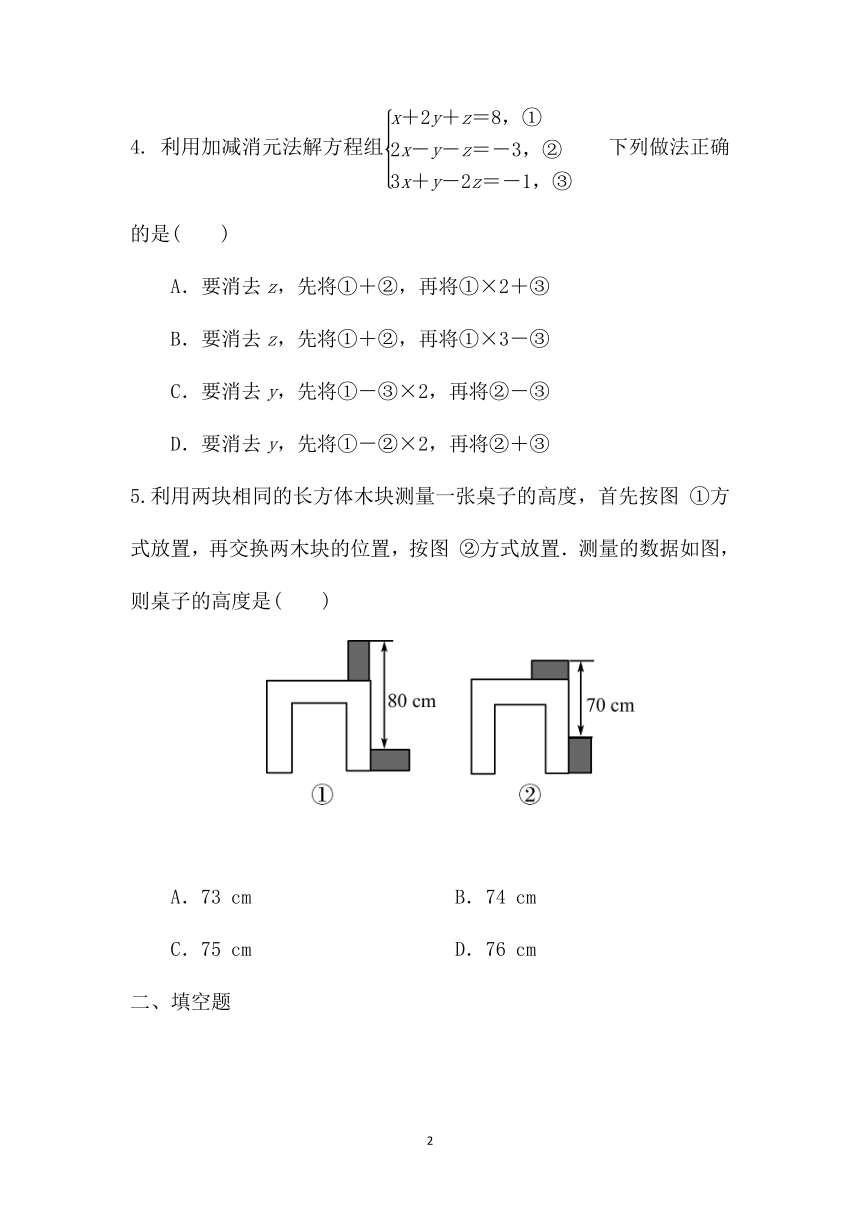
5.利用两块相同的长方体木块测量一张桌子的高度,首先按图 ①方式放置,再交换两木块的位置,按图 ②方式放置.测量的数据如图,则桌子的高度是( )
A.73 cm B.74 cm
C.75 cm D.76 cm
二、填空题
6.对于方程组
(1)若先消去x,可得含y,z的方程组是_____________________;
(2)若先消去y,可得含x,z的方程组是________________;
(3)若先消去z,可得含x,y的方程组是________________.
7.(2021河南周口沈丘期末)若一个三角形的三边长分别为a cm,b cm,c cm,此三角形周长为18 cm,且a+b=2c,b=2a,则a= ,b= ,c= .
8.(2021湖南长沙雨花广益中学月考)已知等式y=ax2+bx+c,当x=-1时,y=4;当x=1时,y=8;当x=2时,y=25,则当x=3时,y= .
9.(2021重庆开州期末)为庆祝建党一百周年,某学校欲购买A,B,C三种花卉各100束装饰庆典会场.已知购买4束A花卉,7束B花卉,1束C花卉,共用45元;购买3束A花卉,5束B花卉,1束C花卉,共用35元.则学校购买这批装饰庆典会场的花卉一共要用 元.
三、解答题
10.在等式y=ax2+bx+c中,当x=-1时,y=4;
当x=2时,y=4;当x=1时,y=2.
(1)求a,b,c的值;
(2)当x=-2时,求y的值.
11.有一个三位数,它的十位上的数字等于个位上的数字与百位上的数字的和,个位上的数字与十位上的数字之和等于8,百位上的数字与个位上的数字对调后所得的三位数比原来的三位数大99.求原来的三位数.
12.(2021北京首都师大附属实验学校月考)小铃观察三元一次方程组各个未知数的系数特点,先用②-①,得3x+y=2,记为④,消掉未知数z,那么下一步应完成的是 ,得到 ,记为⑤,由④⑤可解得x,y的值,通过代入x,y的值求出未知数z的值,完成这个三元一次方程组的求解.
13.(2021上海宝山期末)解方程组:
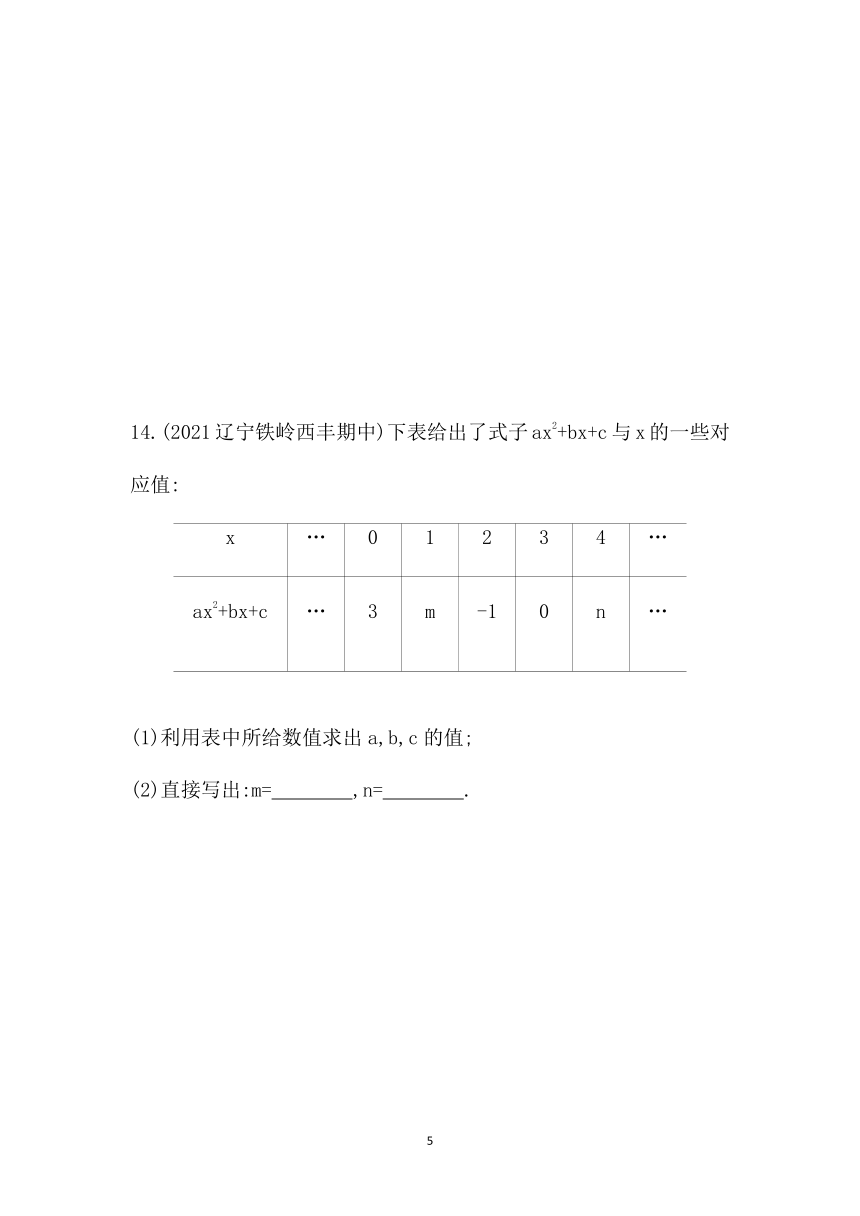
14.(2021辽宁铁岭西丰期中)下表给出了式子ax2+bx+c与x的一些对应值:
x … 0 1 2 3 4 …
ax2+bx+c … 3 m -1 0 n …
(1)利用表中所给数值求出a,b,c的值;
(2)直接写出:m= ,n= .
15.(2021江苏苏州一模)阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+22y=10变形为2(4x+10y)+2y=10③,把方程①代入③,得2×6+2y=10,则y=-1;把y=-1代入①,得x=4,所以方程组的解为
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组
(2)已知x、y、z满足试求z的值.
一、选择题
1.答案 B 方程①+②×2可直接消去未知数y,即可与方程③组成一个关于x、z的二元一次方程组,
∴要使运算简便,消元的方法应选取先消去y,故选B.
2.答案 D
②+③得x+y=7,④
①+④得2x=8,即x=4,
把x=4代入①得y=3,
把x=4代入③得z=2,
则方程组的解为
故选D.
3.答案 D 设甲、乙、丙三种商品的单价分别为x元、y元、z元.
根据题意可得①+②得5x+5y+5z=1 000,
则x+y+z=200,即购买甲、乙、丙各一件时应该付款200元.故选D.
4. 答案 A
5. 答案 C
二、填空题
6.答案 (1)
(2)
(3)
7.答案 4;8;6
解析 由题意得
将②代入①,得c=6,则
解得
∴方程组的解为
故答案为4;8;6.
8.答案 52
解析 由题意得解得
所以等式为y=5x2+2x+1,
当x=3时,y=5×32+2×3+1=52,故答案为52.
9.答案 1 500
解析 设A种花卉x元/束,B种花卉y元/束,C种花卉z元/束,
根据题意,得
①-②,得x+2y=10③,
①-③×4,得z-y=5④,
③+④,得x+y+z=15,∴100(x+y+z)=100×15=1 500(元).故答案为1 500.
三、解答题
10.解析 (1) (2)8
11.解析 原来的三位数为253.
12.解析 ②-①,得3x+y=2④,③-①,得8x+2y=6⑤,
由④⑤可得到关于x,y的二元一次方程组解得
把x=1,y=-1代入①得,z=1,所以原方程组的解为
13.解析
②-①,得3x+3y=3,④
③-②,得21x+3y=57,⑤
⑤-④,得18x=54,
解得x=3,
将x=3代入④,得9+3y=3,
解得y=-2,
将x=3,y=-2代入①,得3+2+z=0,
解得z=-5,
∴方程组的解为
14.解析 (1)根据题意得解得
∴a,b,c的值分别为1,-4,3.
(2)当x=1时,x2-4x+3=1-4+3=0,
当x=4时,x2-4x+3=16-16+3=3,
∴m=0,n=3.
15.解析 (1)
将②变形得3(2x-3y)+4y=11,③
将①代入③得3×7+4y=11,
解得y=-,
把y=-代入①得x=-,
∴方程组的解为
(2)
由①得3(x+4y)-2z=47,③
由②得2(x+4y)+z=36,④
③×2-④×3得-7z=-14,解得z=2.
1
班级 姓名
第八章 二元一次方程组
8.4 三元一次方程组的解法
测试时间:20分钟
一、选择题
1.(2021湖南长沙开福期中)观察方程组的系数特征,若要使求解简便,消元的方法应选取( )
A.先消去x B.先消去y
C.先消去z D.以上说法都不对
2.(2021河北秦皇岛青龙期末)三元一次方程组的解是( )
A. B. C. D.
3.某天,小李在某电商平台上选择了甲、乙、丙三种商品,当购物车内选3件甲,2件乙,1件丙时显示价格为420元;当选2件甲,3件乙,4件丙时显示价格为580元,那么购买甲、乙、丙各一件时应该付款( )
A.580元 B.500元 C.420元 D.200元
4. 利用加减消元法解方程组下列做法正确的是( )
A.要消去z,先将①+②,再将①×2+③
B.要消去z,先将①+②,再将①×3-③
C.要消去y,先将①-③×2,再将②-③
D.要消去y,先将①-②×2,再将②+③
5.利用两块相同的长方体木块测量一张桌子的高度,首先按图 ①方式放置,再交换两木块的位置,按图 ②方式放置.测量的数据如图,则桌子的高度是( )
A.73 cm B.74 cm
C.75 cm D.76 cm
二、填空题
6.对于方程组
(1)若先消去x,可得含y,z的方程组是_____________________;
(2)若先消去y,可得含x,z的方程组是________________;
(3)若先消去z,可得含x,y的方程组是________________.
7.(2021河南周口沈丘期末)若一个三角形的三边长分别为a cm,b cm,c cm,此三角形周长为18 cm,且a+b=2c,b=2a,则a= ,b= ,c= .
8.(2021湖南长沙雨花广益中学月考)已知等式y=ax2+bx+c,当x=-1时,y=4;当x=1时,y=8;当x=2时,y=25,则当x=3时,y= .
9.(2021重庆开州期末)为庆祝建党一百周年,某学校欲购买A,B,C三种花卉各100束装饰庆典会场.已知购买4束A花卉,7束B花卉,1束C花卉,共用45元;购买3束A花卉,5束B花卉,1束C花卉,共用35元.则学校购买这批装饰庆典会场的花卉一共要用 元.
三、解答题
10.在等式y=ax2+bx+c中,当x=-1时,y=4;
当x=2时,y=4;当x=1时,y=2.
(1)求a,b,c的值;
(2)当x=-2时,求y的值.
11.有一个三位数,它的十位上的数字等于个位上的数字与百位上的数字的和,个位上的数字与十位上的数字之和等于8,百位上的数字与个位上的数字对调后所得的三位数比原来的三位数大99.求原来的三位数.
12.(2021北京首都师大附属实验学校月考)小铃观察三元一次方程组各个未知数的系数特点,先用②-①,得3x+y=2,记为④,消掉未知数z,那么下一步应完成的是 ,得到 ,记为⑤,由④⑤可解得x,y的值,通过代入x,y的值求出未知数z的值,完成这个三元一次方程组的求解.
13.(2021上海宝山期末)解方程组:
14.(2021辽宁铁岭西丰期中)下表给出了式子ax2+bx+c与x的一些对应值:
x … 0 1 2 3 4 …
ax2+bx+c … 3 m -1 0 n …
(1)利用表中所给数值求出a,b,c的值;
(2)直接写出:m= ,n= .
15.(2021江苏苏州一模)阅读材料:善于思考的小明在解方程组时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+22y=10变形为2(4x+10y)+2y=10③,把方程①代入③,得2×6+2y=10,则y=-1;把y=-1代入①,得x=4,所以方程组的解为
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组
(2)已知x、y、z满足试求z的值.
一、选择题
1.答案 B 方程①+②×2可直接消去未知数y,即可与方程③组成一个关于x、z的二元一次方程组,
∴要使运算简便,消元的方法应选取先消去y,故选B.
2.答案 D
②+③得x+y=7,④
①+④得2x=8,即x=4,
把x=4代入①得y=3,
把x=4代入③得z=2,
则方程组的解为
故选D.
3.答案 D 设甲、乙、丙三种商品的单价分别为x元、y元、z元.
根据题意可得①+②得5x+5y+5z=1 000,
则x+y+z=200,即购买甲、乙、丙各一件时应该付款200元.故选D.
4. 答案 A
5. 答案 C
二、填空题
6.答案 (1)
(2)
(3)
7.答案 4;8;6
解析 由题意得
将②代入①,得c=6,则
解得
∴方程组的解为
故答案为4;8;6.
8.答案 52
解析 由题意得解得
所以等式为y=5x2+2x+1,
当x=3时,y=5×32+2×3+1=52,故答案为52.
9.答案 1 500
解析 设A种花卉x元/束,B种花卉y元/束,C种花卉z元/束,
根据题意,得
①-②,得x+2y=10③,
①-③×4,得z-y=5④,
③+④,得x+y+z=15,∴100(x+y+z)=100×15=1 500(元).故答案为1 500.
三、解答题
10.解析 (1) (2)8
11.解析 原来的三位数为253.
12.解析 ②-①,得3x+y=2④,③-①,得8x+2y=6⑤,
由④⑤可得到关于x,y的二元一次方程组解得
把x=1,y=-1代入①得,z=1,所以原方程组的解为
13.解析
②-①,得3x+3y=3,④
③-②,得21x+3y=57,⑤
⑤-④,得18x=54,
解得x=3,
将x=3代入④,得9+3y=3,
解得y=-2,
将x=3,y=-2代入①,得3+2+z=0,
解得z=-5,
∴方程组的解为
14.解析 (1)根据题意得解得
∴a,b,c的值分别为1,-4,3.
(2)当x=1时,x2-4x+3=1-4+3=0,
当x=4时,x2-4x+3=16-16+3=3,
∴m=0,n=3.
15.解析 (1)
将②变形得3(2x-3y)+4y=11,③
将①代入③得3×7+4y=11,
解得y=-,
把y=-代入①得x=-,
∴方程组的解为
(2)
由①得3(x+4y)-2z=47,③
由②得2(x+4y)+z=36,④
③×2-④×3得-7z=-14,解得z=2.
1
