2021-2022学年冀教版九年级上学期数学期末练习试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级上学期数学期末练习试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 463.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 10:32:26 | ||
图片预览




文档简介
2021-2022学年冀教新版九年级上学期数学期末练习试卷
一.选择题(共16小题,满分42分)
1.若y=(m+1)x是关于x的二次函数,则m的值为( )
A.﹣2 B.1 C.﹣2或1 D.2或1
2.在△ABC中,∠ABC=90°.若AC=100,sinA=,则AB的长是( )
A. B. C.60 D.80
3.对于双曲线,x>0时,y随x的增大而增大,则k的取值范围为( )
A.k<2 B.k≤2 C.k>2 D.k≥2
4.一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是( )
A.5cm B.6cm C.()cm D.()cm
5.如图,水库大坝截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( )
A.55m B.60m C.65m D.70m
6.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数为( )
A.30° B.45° C.60° D.75°
7.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )
A.4m B.6m C.8m D.10m
8.在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
9.如图,点I为△ABC的内心,AB=4cm,AC=3cm,BC=2cm,将∠ACB平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.1cm B.2cm C.3cm D.4cm
10.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
11.已知圆心角为120°的扇形的面积为12π,则扇形的半径为( )
A.4 B.6 C.4 D.6
12.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A. B. C. D.
13.四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A.甲 B.乙 C.丙 D.丁
14.一个几何体的三视图如图所示,则这个几何体的表面积是( )
A.5cm2 B.8cm2 C.9cm2 D.10cm2
15.已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如表:
x … ﹣1 0 1 2 3 …
y … 3 0 ﹣1 m 3 …
有以下几个结论:
①抛物线y=ax2+bx+c的开口向下;
②抛物线y=ax2+bx+c的对称轴为直线x=﹣1;
③方程ax2+bx+c=0的根为0和2;
④当y>0时,x的取值范围是x<0或x>2;
其中正确的是( )
A.①④ B.②④ C.②③ D.③④
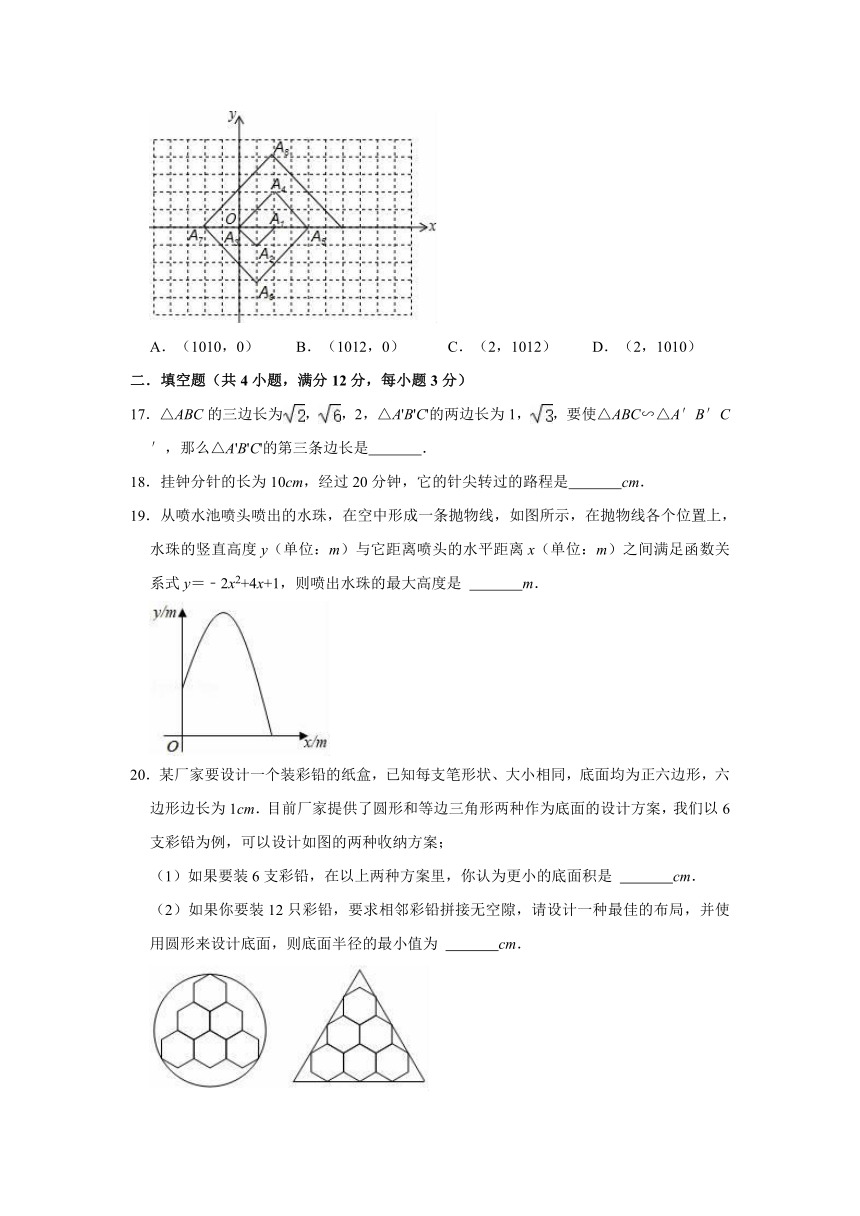
16.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为( )
A.(1010,0) B.(1012,0) C.(2,1012) D.(2,1010)
二.填空题(共4小题,满分12分,每小题3分)
17.△ABC的三边长为,,2,△A'B'C'的两边长为1,,要使△ABC∽△A′B′C′,那么△A'B'C'的第三条边长是 .
18.挂钟分针的长为10cm,经过20分钟,它的针尖转过的路程是 cm.
19.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
20.某厂家要设计一个装彩铅的纸盒,已知每支笔形状、大小相同,底面均为正六边形,六边形边长为1cm.目前厂家提供了圆形和等边三角形两种作为底面的设计方案,我们以6支彩铅为例,可以设计如图的两种收纳方案;
(1)如果要装6支彩铅,在以上两种方案里,你认为更小的底面积是 cm.
(2)如果你要装12只彩铅,要求相邻彩铅拼接无空隙,请设计一种最佳的布局,并使用圆形来设计底面,则底面半径的最小值为 cm.
三.解答题(共6小题,满分66分)
21.(10分)某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同
(1)求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
22.(10分)深圳某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生.
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学九年级共有700名学生,请你估计该中学九年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
23.(10分)如图所示,一次函数y=kx+b的图象与反比例函数y=的图象交于A(1,t+1),B(t﹣5,﹣1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=图象上任意两点,且满足c=n+1时,求的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<﹣3,0<x2<1,当x1x2=﹣3时,判断四边形NFEM的形状.并说明理由.
24.(12分)已知点A,B,C是⊙O上的三个点,∠AOB=120°.
(Ⅰ)如图①,若AC=BC,求∠C和∠CAO的大小;
(Ⅱ)如图②,过点C作⊙O的切线,交BA的延长线于点D,若AC=AD,求∠CAO的大小.
25.(12分)高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) 0 0.5 1 1.5 2 …
h(m) 0 8.75 15 18.75 20 …
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
26.(12分)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
参考答案与试题解析
一.选择题(共16小题,满分42分)
1.解:若y=(m+1)x是关于x的二次函数,则m2+m=2且m+1≠0.,
解得:m=﹣2或m=1.
故选:C.
2.解:∵AC=100,sinA=,
∴BC=60,
∴AB==80,
故选:D.
3.解:∵双曲线,x>0时,y随x的增大而增大,
∴k﹣2<0
∴k<2,
故选:A.
4.解:∵斜边AB=8cm,∠A=30°,
∴BC=4cm,AC=4cm,周长是12+4cm,
连接BE,过E作EM⊥BC于M,
∵点E到边AB,BC的距离均为1,
∴∠ABE=∠EBC=∠ABC=30°(在角内部,到角两边距离相等的点在角平分线上),EM=1cm,
∴BM=cm.
则EF=4﹣1﹣=3﹣cm.
∴△ABC∽△DEF,
相似比是=,
相似三角形周长的比等于相似比,
因而=,
解得△DEF的周长是6cm.
故选:B.
5.解:∵DE=20m,DE:AE=4:3,
∴AE=15m,
∵CF=DE=20m,CF:BF=1:2,
∴BF=40m,
∴AB=AE+EF+BF=15+10+40=65m.
故选:C.
6.解:∵四边形ABCO是平行四边形,
∴∠AOC=∠B,
∵∠B+∠D=180°,∠AOC=2∠D,
∴2∠D+∠D=180°,
∴∠D=60°.
故选:C.
7.解:根据垂径定理可知AD=8,
在直角△AOD中,根据勾股定理得:
OA2=AD2+OD2
则102=82+(10﹣CD)2
解得:CD=16或4,
根据题中OA=10m,可知CD=16不合题意,故舍去,
所以取CD=4m.
故选:A.
8.解:∵点(﹣2,3)到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
∴圆与y轴相交,与x轴相切.
故选:B.
9.解:如图,连接AI,BI,
∵点I为△ABC的内心,
∴IA和IB分别平分∠CAB和∠CBA,
∴∠CAI=∠DAI,∠CBI=∠EBI,
∵将∠ACB平移,使其顶点与点I重合,
∴DI∥AC,EI∥BC,
∴∠CAI=∠DIA,∠CBI=∠EIB,
∴∠DAI=∠DIA,∠EBI=∠EIB,
∴DA=DI,EB=EI,
∴DE+DI+EI=DE+DA+EB=AB=4.
所以图中阴影部分的周长为4.
故选:D.
10.解:A、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
B、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,
故本选项符合题意;
D、阴影三角形中,∠A的两边分别为6﹣2=4,8﹣5=3,则两三角形对应边成比例且夹角相等,故两三角形相似,
故本选项不符合题意.
故选:C.
11.解:设该扇形的半径是r,则
12π=,
解得r=6.
故选:B.
12.解:用列表法表示所有可能出现的结果如下:
共有12种等可能出现的结果,其中少于30元的有4种,
∴该顾客所获得返现金额低于30元的概率是=,
故选:D.
13.解:假设甲和丙的结论正确,则,
解得:,
∴抛物线的解析式为y=x2﹣2x+4.
当x=﹣1时,y=x2﹣2x+4=7,
∴乙的结论不正确;
当x=2时,y=x2﹣2x+4=4,
∴丁的结论正确.
∵四位同学中只有一位发现的结论是错误的,
∴假设成立.
故选:B.
14.解:由题意推知几何体是长方体,长、宽、高分别1cm、1cm、2cm,
所以其面积为:2×(1×1+1×2+1×2)=10(cm2).
故选:D.
15.解:设抛物线的解析式为y=ax2+bx+c,
将(﹣1,3)、(0,0)、(3,3)代入得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x=x(x﹣2)=(x﹣1)2﹣1,
由a=1>0知抛物线的开口向上,故①错误;
抛物线的对称轴为直线x=1,故②错误;
当y=0时,x(x﹣2)=0,解得x=0或x=2,
∴方程ax2+bx+c=0的根为0和2,故③正确;
当y>0时,x(x﹣2)>0,解得x<0或x>2,故④正确;
故选:D.
16.解:观察点的坐标变化发现:
当脚码为偶数时的点的坐标,得到规律:
当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,
当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,
因为2020能被4整除,
所以横坐标为2,纵坐标为1010,
故选:D.
二.填空题(共4小题,满分12分,每小题3分)
17.解:∵△ABC的三边长分别为:,,2,
∴△ABC的三边长之比为,1::,比例系数是,
∵△A′B′C′的两边长分别为1和,△ABC∽△A′B′C′,
∴△A′B′C′的第三边的长应等于.
故答案为:.
18.解:分针20分钟转20×6°=120°,
所以分针的针尖转过的路程==(cm).
故答案为.
19.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
20.解:(1)如图1中,圆的半径为3,
∴底面积为9π(cm2).
如图2中,连接OA,OD.
∵OD=2cm,∠OAD=30°,∠ADO=90°,
∴OA=2OD=4cm,
∴AD==2(cm),
∴等边三角形的边长AC=4(cm),
∴底面积=×(4)2=12(cm2)<9π(cm2),
∴等边三角形作为底面时,面积比较小,底面积为12cm2
如图3中,设计方案如图3所示,
在Rt△OET中,ET=1cm,OE=2cm,
∴OT===(cm),
∴底面半径的最小值为cm.
故答案为:.
三.解答题(共6小题,满分66分)
21.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元.
22.解:(1)10÷20%=50(名),
即本次抽样调查共抽取了50名学生,
故答案为:50;
(2)测试结果为C等级的学生数为:50﹣10﹣20﹣4=16(名),
故答案为:16,补全条形图如下:
(3)700×=56(名),
即估计该中学九年级学生中体能测试结果为D等级的学生有56名;
(4)画树状图如图:
共有12个等可能的结果,所抽取的两人恰好都是男生的结果有2个,
∴抽取的两人恰好都是男生的概率==.
23.解:(1)∵A(1,t+1),B(t﹣5,﹣1)两点在反比例函数y=的图象上,
∴t+1=﹣(t﹣5)=m,
即t+1=5﹣t,解得t=2.
当t=2时,A(1,3),B(﹣3,﹣1),m=3,
∴反比例函数的解析式为y=.
∵A、B在一次函数y=kx+b的图象上,
∴,解得,
∴一次函数的解析式为y=x+2;
(2)∵点(c,p)和(n,q)在反比例函数y=图象上,
∴cp=nq=m=3,
∴c=,n=,
∵c=n+1,即,
∴;
(3)四边形NFEM为平行四边形,如图,理由如下:
由题意可知,M(x1,x1+2),N(x2,x2+2),E(x1,),F(x2,),
即ME=﹣(x1+2),NF=﹣(x2+2),
∵ME﹣NF=(﹣x1﹣2)﹣(﹣x2﹣2)=()﹣(x1﹣x2),
即ME﹣NF=﹣(x1﹣x2)
∵x1<﹣3,0<x2<1,
∴x1﹣x2≠0,
∵x1x2=﹣3,
∴ME﹣NF=0,
即ME=NF
又∵ME∥NF,
∴四边形NFEM为平行四边形.
24.解:(Ⅰ)连接OC,
∵∠AOB=120°,
∴∠ACB=∠AOB=60°,
∵AC=BC,
∴∠AOC=∠BOC,
∴∠AOC==120°,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAO=(180°﹣∠AOC)==30°;
(Ⅱ)连接OC并延长交⊙O于点E,连接AE,
∵OA=OB,∠AOB=120°,
∴∠OBA=30°,
∵CD是⊙O的切线,
∴CE⊥CD,
∴∠ACE+∠ACD=90°,
∵CE为⊙O的直径,
∴∠CAE=90°,
∴∠ACE+∠E=90°,
∴∠ACD=∠E,
∵AC=AD,
∴∠ACD=∠D,
∴∠D=∠ABC=∠AEC,
设∠OBC=x,则∠ABC=30°+x,
∵OB=OC,
∴∠OBC=∠OCB=x,
在△BCD中,∠D+∠ABC+∠DCB=180°,
∴30°+x+30°+x+90°+x=180°,
∴x=10°,
∴∠OBC=10°,
∴∠D=∠ABC=∠ACD=40°,
∴∠ACO=∠CAO=90°﹣∠ACD=90°﹣40°=50°.
25.解:(1)∵t=0时,h=0,
∴设h与t之间的函数关系式为h=at2+bt(a≠0),
∵t=1时,h=15;t=2时,h=20,
∴,
解得,
∴h与t之间的函数关系式为h=﹣5t2+20t;
(2)小球飞行3秒时,t=3(s),此时h=﹣5×32+20×3=15(m).
答:小球飞行3s时的高度为15米.
26.解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,
解得:b=﹣4,c=3,
∴二次函数的表达式为:y=x2﹣4x+3;
(2)令y=0,则x2﹣4x+3=0,
解得:x=1或x=3,
∴B(3,0),
∴BC=3,
点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,
①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3
∴P1(0,3+3),P2(0,3﹣3);
②当BP=BC时,OP=OC=3,
∴P3(0,﹣3);
③当PB=PC时,
∵OC=OB=3
∴此时P与O重合,
∴P4(0,0);
综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);
(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,
∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,
即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.
一.选择题(共16小题,满分42分)
1.若y=(m+1)x是关于x的二次函数,则m的值为( )
A.﹣2 B.1 C.﹣2或1 D.2或1
2.在△ABC中,∠ABC=90°.若AC=100,sinA=,则AB的长是( )
A. B. C.60 D.80
3.对于双曲线,x>0时,y随x的增大而增大,则k的取值范围为( )
A.k<2 B.k≤2 C.k>2 D.k≥2
4.一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1cm,那么△DEF的周长是( )
A.5cm B.6cm C.()cm D.()cm
5.如图,水库大坝截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则下底AB的长为( )
A.55m B.60m C.65m D.70m
6.如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC的度数为( )
A.30° B.45° C.60° D.75°
7.如图,有一圆弧形桥拱,拱形的半径OA=10m,桥拱的跨度AB=16m,则拱高CD为( )
A.4m B.6m C.8m D.10m
8.在平面直角坐标系中,以点(﹣2,3)为圆心,半径为3的圆一定( )
A.与x轴相切,与y轴相切 B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切 D.与x轴相交,与y轴相交
9.如图,点I为△ABC的内心,AB=4cm,AC=3cm,BC=2cm,将∠ACB平移,使其顶点与点I重合,则图中阴影部分的周长为( )
A.1cm B.2cm C.3cm D.4cm
10.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
11.已知圆心角为120°的扇形的面积为12π,则扇形的半径为( )
A.4 B.6 C.4 D.6
12.某超市为了吸引顾客,设计了一种返现促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样,规定:顾客在本超市一次性消费满200元,就可以在箱子里一次性摸出两个小球,两球数字之和记为返现金额.某顾客刚好消费200元,则该顾客所获得返现金额低于30元的概率是( )
A. B. C. D.
13.四位同学在研究函数y=x2+bx+c(b,c是常数)时,甲发现当x=1时,函数有最小值;乙发现﹣1是方程x2+bx+c=0的一个根;丙发现函数的最小值为3;丁发现当x=2时,y=4,已知这四位同学中只有一位发现的结论是错误的,则该同学是( )
A.甲 B.乙 C.丙 D.丁
14.一个几何体的三视图如图所示,则这个几何体的表面积是( )
A.5cm2 B.8cm2 C.9cm2 D.10cm2
15.已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如表:
x … ﹣1 0 1 2 3 …
y … 3 0 ﹣1 m 3 …
有以下几个结论:
①抛物线y=ax2+bx+c的开口向下;
②抛物线y=ax2+bx+c的对称轴为直线x=﹣1;
③方程ax2+bx+c=0的根为0和2;
④当y>0时,x的取值范围是x<0或x>2;
其中正确的是( )
A.①④ B.②④ C.②③ D.③④
16.如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7……,都是斜边在x轴上,斜边长分别为2,4,6,……的等腰直角三角形,若A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2020的坐标为( )
A.(1010,0) B.(1012,0) C.(2,1012) D.(2,1010)
二.填空题(共4小题,满分12分,每小题3分)
17.△ABC的三边长为,,2,△A'B'C'的两边长为1,,要使△ABC∽△A′B′C′,那么△A'B'C'的第三条边长是 .
18.挂钟分针的长为10cm,经过20分钟,它的针尖转过的路程是 cm.
19.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
20.某厂家要设计一个装彩铅的纸盒,已知每支笔形状、大小相同,底面均为正六边形,六边形边长为1cm.目前厂家提供了圆形和等边三角形两种作为底面的设计方案,我们以6支彩铅为例,可以设计如图的两种收纳方案;
(1)如果要装6支彩铅,在以上两种方案里,你认为更小的底面积是 cm.
(2)如果你要装12只彩铅,要求相邻彩铅拼接无空隙,请设计一种最佳的布局,并使用圆形来设计底面,则底面半径的最小值为 cm.
三.解答题(共6小题,满分66分)
21.(10分)某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同
(1)求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
22.(10分)深圳某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了 名学生.
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学九年级共有700名学生,请你估计该中学九年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.
23.(10分)如图所示,一次函数y=kx+b的图象与反比例函数y=的图象交于A(1,t+1),B(t﹣5,﹣1)两点.
(1)求一次函数和反比例函数的解析式;
(2)若点(c,p)和(n,q)是反比例函数y=图象上任意两点,且满足c=n+1时,求的值.
(3)若点M(x1,y1)和N(x2,y2)在直线AB(不与A、B重合)上,过M、N两点分别作y轴的平行线交双曲线于E、F,已知x1<﹣3,0<x2<1,当x1x2=﹣3时,判断四边形NFEM的形状.并说明理由.
24.(12分)已知点A,B,C是⊙O上的三个点,∠AOB=120°.
(Ⅰ)如图①,若AC=BC,求∠C和∠CAO的大小;
(Ⅱ)如图②,过点C作⊙O的切线,交BA的延长线于点D,若AC=AD,求∠CAO的大小.
25.(12分)高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) 0 0.5 1 1.5 2 …
h(m) 0 8.75 15 18.75 20 …
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
26.(12分)如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形?若存在.请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从 点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.
参考答案与试题解析
一.选择题(共16小题,满分42分)
1.解:若y=(m+1)x是关于x的二次函数,则m2+m=2且m+1≠0.,
解得:m=﹣2或m=1.
故选:C.
2.解:∵AC=100,sinA=,
∴BC=60,
∴AB==80,
故选:D.
3.解:∵双曲线,x>0时,y随x的增大而增大,
∴k﹣2<0
∴k<2,
故选:A.
4.解:∵斜边AB=8cm,∠A=30°,
∴BC=4cm,AC=4cm,周长是12+4cm,
连接BE,过E作EM⊥BC于M,
∵点E到边AB,BC的距离均为1,
∴∠ABE=∠EBC=∠ABC=30°(在角内部,到角两边距离相等的点在角平分线上),EM=1cm,
∴BM=cm.
则EF=4﹣1﹣=3﹣cm.
∴△ABC∽△DEF,
相似比是=,
相似三角形周长的比等于相似比,
因而=,
解得△DEF的周长是6cm.
故选:B.
5.解:∵DE=20m,DE:AE=4:3,
∴AE=15m,
∵CF=DE=20m,CF:BF=1:2,
∴BF=40m,
∴AB=AE+EF+BF=15+10+40=65m.
故选:C.
6.解:∵四边形ABCO是平行四边形,
∴∠AOC=∠B,
∵∠B+∠D=180°,∠AOC=2∠D,
∴2∠D+∠D=180°,
∴∠D=60°.
故选:C.
7.解:根据垂径定理可知AD=8,
在直角△AOD中,根据勾股定理得:
OA2=AD2+OD2
则102=82+(10﹣CD)2
解得:CD=16或4,
根据题中OA=10m,可知CD=16不合题意,故舍去,
所以取CD=4m.
故选:A.
8.解:∵点(﹣2,3)到x轴的距离是3,等于半径,
到y轴的距离是2,小于半径,
∴圆与y轴相交,与x轴相切.
故选:B.
9.解:如图,连接AI,BI,
∵点I为△ABC的内心,
∴IA和IB分别平分∠CAB和∠CBA,
∴∠CAI=∠DAI,∠CBI=∠EBI,
∵将∠ACB平移,使其顶点与点I重合,
∴DI∥AC,EI∥BC,
∴∠CAI=∠DIA,∠CBI=∠EIB,
∴∠DAI=∠DIA,∠EBI=∠EIB,
∴DA=DI,EB=EI,
∴DE+DI+EI=DE+DA+EB=AB=4.
所以图中阴影部分的周长为4.
故选:D.
10.解:A、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
B、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,
故本选项符合题意;
D、阴影三角形中,∠A的两边分别为6﹣2=4,8﹣5=3,则两三角形对应边成比例且夹角相等,故两三角形相似,
故本选项不符合题意.
故选:C.
11.解:设该扇形的半径是r,则
12π=,
解得r=6.
故选:B.
12.解:用列表法表示所有可能出现的结果如下:
共有12种等可能出现的结果,其中少于30元的有4种,
∴该顾客所获得返现金额低于30元的概率是=,
故选:D.
13.解:假设甲和丙的结论正确,则,
解得:,
∴抛物线的解析式为y=x2﹣2x+4.
当x=﹣1时,y=x2﹣2x+4=7,
∴乙的结论不正确;
当x=2时,y=x2﹣2x+4=4,
∴丁的结论正确.
∵四位同学中只有一位发现的结论是错误的,
∴假设成立.
故选:B.
14.解:由题意推知几何体是长方体,长、宽、高分别1cm、1cm、2cm,
所以其面积为:2×(1×1+1×2+1×2)=10(cm2).
故选:D.
15.解:设抛物线的解析式为y=ax2+bx+c,
将(﹣1,3)、(0,0)、(3,3)代入得:
,
解得:,
∴抛物线的解析式为y=x2﹣2x=x(x﹣2)=(x﹣1)2﹣1,
由a=1>0知抛物线的开口向上,故①错误;
抛物线的对称轴为直线x=1,故②错误;
当y=0时,x(x﹣2)=0,解得x=0或x=2,
∴方程ax2+bx+c=0的根为0和2,故③正确;
当y>0时,x(x﹣2)>0,解得x<0或x>2,故④正确;
故选:D.
16.解:观察点的坐标变化发现:
当脚码为偶数时的点的坐标,得到规律:
当脚码是2、6、10…时,横坐标为1,纵坐标为脚码的一半的相反数,
当脚码是4、8、12.…时,横坐标是2,纵坐标为脚码的一半,
因为2020能被4整除,
所以横坐标为2,纵坐标为1010,
故选:D.
二.填空题(共4小题,满分12分,每小题3分)
17.解:∵△ABC的三边长分别为:,,2,
∴△ABC的三边长之比为,1::,比例系数是,
∵△A′B′C′的两边长分别为1和,△ABC∽△A′B′C′,
∴△A′B′C′的第三边的长应等于.
故答案为:.
18.解:分针20分钟转20×6°=120°,
所以分针的针尖转过的路程==(cm).
故答案为.
19.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
20.解:(1)如图1中,圆的半径为3,
∴底面积为9π(cm2).
如图2中,连接OA,OD.
∵OD=2cm,∠OAD=30°,∠ADO=90°,
∴OA=2OD=4cm,
∴AD==2(cm),
∴等边三角形的边长AC=4(cm),
∴底面积=×(4)2=12(cm2)<9π(cm2),
∴等边三角形作为底面时,面积比较小,底面积为12cm2
如图3中,设计方案如图3所示,
在Rt△OET中,ET=1cm,OE=2cm,
∴OT===(cm),
∴底面半径的最小值为cm.
故答案为:.
三.解答题(共6小题,满分66分)
21.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元.
22.解:(1)10÷20%=50(名),
即本次抽样调查共抽取了50名学生,
故答案为:50;
(2)测试结果为C等级的学生数为:50﹣10﹣20﹣4=16(名),
故答案为:16,补全条形图如下:
(3)700×=56(名),
即估计该中学九年级学生中体能测试结果为D等级的学生有56名;
(4)画树状图如图:
共有12个等可能的结果,所抽取的两人恰好都是男生的结果有2个,
∴抽取的两人恰好都是男生的概率==.
23.解:(1)∵A(1,t+1),B(t﹣5,﹣1)两点在反比例函数y=的图象上,
∴t+1=﹣(t﹣5)=m,
即t+1=5﹣t,解得t=2.
当t=2时,A(1,3),B(﹣3,﹣1),m=3,
∴反比例函数的解析式为y=.
∵A、B在一次函数y=kx+b的图象上,
∴,解得,
∴一次函数的解析式为y=x+2;
(2)∵点(c,p)和(n,q)在反比例函数y=图象上,
∴cp=nq=m=3,
∴c=,n=,
∵c=n+1,即,
∴;
(3)四边形NFEM为平行四边形,如图,理由如下:
由题意可知,M(x1,x1+2),N(x2,x2+2),E(x1,),F(x2,),
即ME=﹣(x1+2),NF=﹣(x2+2),
∵ME﹣NF=(﹣x1﹣2)﹣(﹣x2﹣2)=()﹣(x1﹣x2),
即ME﹣NF=﹣(x1﹣x2)
∵x1<﹣3,0<x2<1,
∴x1﹣x2≠0,
∵x1x2=﹣3,
∴ME﹣NF=0,
即ME=NF
又∵ME∥NF,
∴四边形NFEM为平行四边形.
24.解:(Ⅰ)连接OC,
∵∠AOB=120°,
∴∠ACB=∠AOB=60°,
∵AC=BC,
∴∠AOC=∠BOC,
∴∠AOC==120°,
∵OA=OC,
∴∠CAO=∠ACO,
∴∠CAO=(180°﹣∠AOC)==30°;
(Ⅱ)连接OC并延长交⊙O于点E,连接AE,
∵OA=OB,∠AOB=120°,
∴∠OBA=30°,
∵CD是⊙O的切线,
∴CE⊥CD,
∴∠ACE+∠ACD=90°,
∵CE为⊙O的直径,
∴∠CAE=90°,
∴∠ACE+∠E=90°,
∴∠ACD=∠E,
∵AC=AD,
∴∠ACD=∠D,
∴∠D=∠ABC=∠AEC,
设∠OBC=x,则∠ABC=30°+x,
∵OB=OC,
∴∠OBC=∠OCB=x,
在△BCD中,∠D+∠ABC+∠DCB=180°,
∴30°+x+30°+x+90°+x=180°,
∴x=10°,
∴∠OBC=10°,
∴∠D=∠ABC=∠ACD=40°,
∴∠ACO=∠CAO=90°﹣∠ACD=90°﹣40°=50°.
25.解:(1)∵t=0时,h=0,
∴设h与t之间的函数关系式为h=at2+bt(a≠0),
∵t=1时,h=15;t=2时,h=20,
∴,
解得,
∴h与t之间的函数关系式为h=﹣5t2+20t;
(2)小球飞行3秒时,t=3(s),此时h=﹣5×32+20×3=15(m).
答:小球飞行3s时的高度为15米.
26.解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c,
解得:b=﹣4,c=3,
∴二次函数的表达式为:y=x2﹣4x+3;
(2)令y=0,则x2﹣4x+3=0,
解得:x=1或x=3,
∴B(3,0),
∴BC=3,
点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图1,
①当CP=CB时,PC=3,∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3
∴P1(0,3+3),P2(0,3﹣3);
②当BP=BC时,OP=OC=3,
∴P3(0,﹣3);
③当PB=PC时,
∵OC=OB=3
∴此时P与O重合,
∴P4(0,0);
综上所述,点P的坐标为:(0,3+3)或(0,3﹣3)或(0,﹣3)或(0,0);
(3)如图2,设A运动时间为t,由AB=2,得BM=2﹣t,则DN=2t,
∴S△MNB=×(2﹣t)×2t=﹣t2+2t=﹣(t﹣1)2+1,
即当M(2,0)、N(2,2)或(2,﹣2)时△MNB面积最大,最大面积是1.
同课章节目录
