2021-2022学年鲁教版(五四制)七年级数学上册 第1章三角形 期末综合复习训练(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册 第1章三角形 期末综合复习训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 150.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 10:38:45 | ||
图片预览




文档简介
2021-2022学年鲁教版七年级数学上册《第1章三角形》期末综合复习训练(附答案)
1.下列各组数可能是一个三角形的边长的是( )
A.4,4,9 B.2,6,8 C.3,4,5 D.1,2,3
2.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.4,5,6 D.5,13,12
3.如图,∠1=( )
A.40° B.50° C.60° D.70°
4.下列各组图形中,AD是△ABC的高的图形是( )
A. B. C. D.
5.已知图中的两个三角形全等,则∠1等于( )
A.72° B.60° C.50° D.58°
6.一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12 B.16 C.20 D.16或20
7.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是( )
A.66° B.36° C.56 D.46°
8.如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
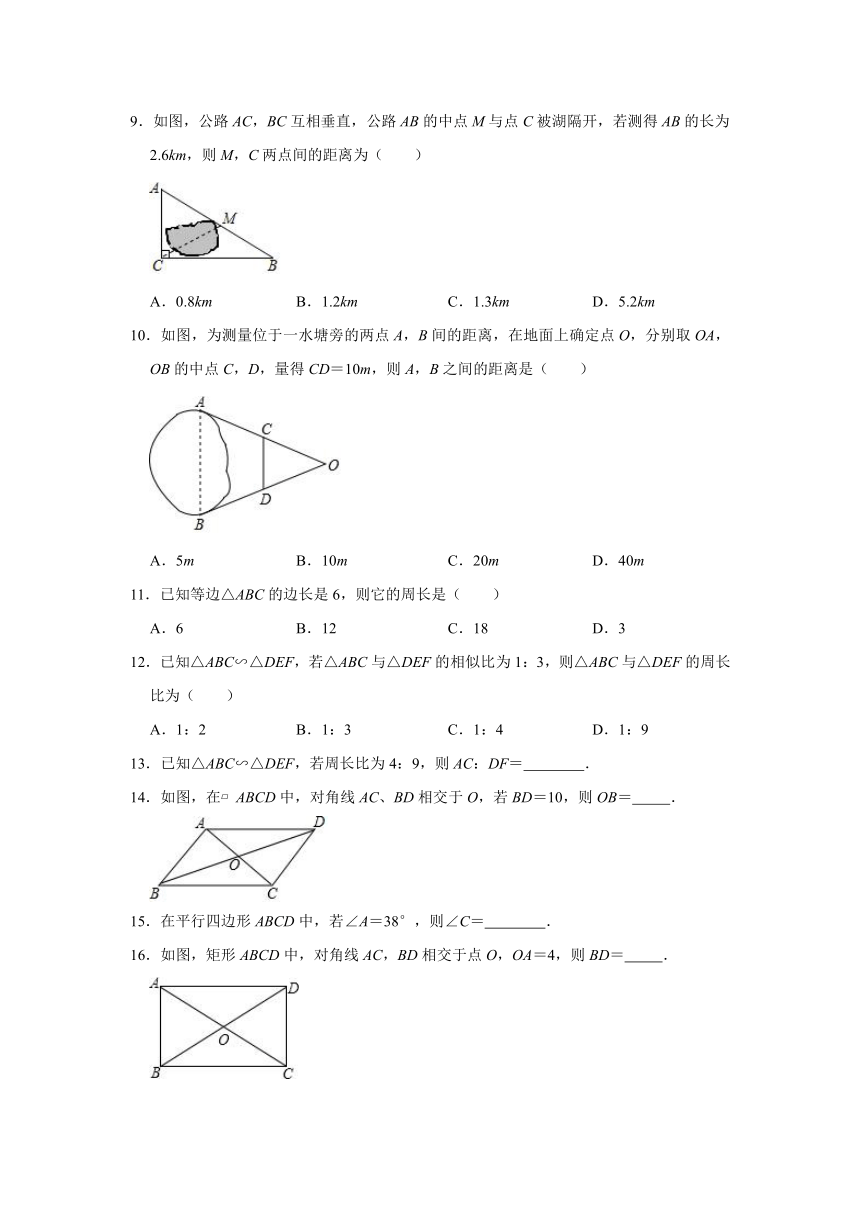
9.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为2.6km,则M,C两点间的距离为( )
A.0.8km B.1.2km C.1.3km D.5.2km
10.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( )
A.5m B.10m C.20m D.40m
11.已知等边△ABC的边长是6,则它的周长是( )
A.6 B.12 C.18 D.3
12.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1:3,则△ABC与△DEF的周长比为( )
A.1:2 B.1:3 C.1:4 D.1:9
13.已知△ABC∽△DEF,若周长比为4:9,则AC:DF= .
14.如图,在 ABCD中,对角线AC、BD相交于O,若BD=10,则OB= .
15.在平行四边形ABCD中,若∠A=38°,则∠C= .
16.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= .
17.如图,在菱形ABCD中,对角线AC=12,BD=16,则这个菱形的周长为 .
18.正方形的边长为,则这个正方形的对角线长为 .
19.如图,在△ADC与△BDC中,∠1=∠2,加上条件 (只填写一个即可),则有△ADC≌△BDC.
20.若△ABC∽△A′B′C′,∠A=50°,∠C=110°,则∠B′的度数为 .
21.已知:如图,OA=OD,OB=OC.求证:△OAB≌△ODC.
22.已知,如图,AB=AD,∠B=∠D,∠1=∠2=60°.
(1)求证:△ADE≌△ABC;
(2)求证:AE=CE.
23.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
24.如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
参考答案
1.解:A、因为4+4<9,所以本组数不能构成三角形.故本选项错误;
B、因为2+6=8,所以本组数不能构成三角形.故本选项错误;
C、因为3+4>5,所以本组数可以构成三角形.故本选项正确;
D、因为1+2=3,所以本组数不能构成三角形.故本选项错误;
故选:C.
2.解:A、12+22=5≠32,故不能组成直角三角形,错误;
B、22+32=13≠42,故不能组成直角三角形,错误;
C、42+52=41≠62,故不能组成直角三角形,错误;
D、52+122=169=132,故能组成直角三角形,正确.
故选:D.
3.解:∠1=130°﹣60°=70°,
故选:D.
4.解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
5.解:如图,由三角形内角和定理得到:∠2=180°﹣50°﹣72°=58°.
∵图中的两个三角形全等,
∴∠1=∠2=58°.
故选:D.
6.解:①当4为腰时,4+4=8,故此种情况不存在;
②当8为腰时,8﹣4<8<8+4,符合题意.
故此三角形的周长=8+8+4=20.
故选:C.
7.解:∵Rt△ABC中,∠C=90°,∠B=54°,
∴∠A=90°﹣∠B=90°﹣54°=36°;
故选:B.
8.解:∵在△ABC中,∠C=90°,∠A=30°,
∴BC=AB=×6=3,
故选:B.
9.解:在Rt△ACB中,点M是AB的中点,
∴CM=AB=×2.6=1.3(km),
故选:C.
10.解:∵点C,D分别是OA,OB的中点,
∴AB=2CD=20(m),
故选:C.
11.解:∵等边△ABC的边长是6,
∴它的周长是6×3=18.
故选:C.
12.解:∵△ABC∽△DEF,△ABC与△DEF的相似比为1:3,
∴△ABC与△DEF的周长比=,
故选:B.
13.解:∵△ABC∽△DEF,周长比为4:9,
∴△ABC与△DEF的相似比为4:9,即AC:DF=4:9,
故答案为:4:9
14.解:∵四边形ABCD是平行四边形,且BD=10,
∴BO=BD=5,
故答案为:5.
15.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A=38°,
∴∠C=38°,
故答案为:38°.
16.解:∵四边形ABCD是矩形,
∴OA=OC=AC,BO=DO=BD,AC=BD,
∴BD=2OA=8,
故答案为:8.
17.解:∵四边形ABCD是菱形,
∴OA=AC=×12=6,OB=BD=×16=8,AC⊥BD,
∴AB===10.
∴此菱形的边长为10,
∴周长为40.
故答案为:40.
18.解:如图,连接AC,
∵四边形ABCD是正方形,
∴AB=BC=,∠B=90°,
∴AC=AB=2,
故答案为:2.
19.解:加上条件AD=BD(答案不唯一),则有△ADC≌△BDC.
理由是:
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
故答案为:AD=BD(答案不唯一).
20.解:∵∠A=50°,∠C=110°,
∴∠B=180°﹣50°﹣110°=20°,
∵△ABC∽△A′B′C′,
∴∠B′=∠B=20°.
故答案为20°.
21.证明:在△OAB和△ODC中
,
∴△OAB≌△ODC(SAS).
22.(1)证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠DAE=∠BAC,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA);
(2)证明:由(1)得△ABC≌△ADE,
∴AE=AC,
∵∠2=60°,
∴△ACE是等边三角形,
∴AE=CE.
23.证明:∵AC∥DE,
∴∠ACB=∠E,∠ACD=∠D,
∵∠ACD=∠B,
∴∠D=∠B,
在△ABC和△EDC中,
∴△ABC≌△CDE(AAS).
24.证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
1.下列各组数可能是一个三角形的边长的是( )
A.4,4,9 B.2,6,8 C.3,4,5 D.1,2,3
2.将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )
A.1,2,3 B.2,3,4 C.4,5,6 D.5,13,12
3.如图,∠1=( )
A.40° B.50° C.60° D.70°
4.下列各组图形中,AD是△ABC的高的图形是( )
A. B. C. D.
5.已知图中的两个三角形全等,则∠1等于( )
A.72° B.60° C.50° D.58°
6.一个等腰三角形的两边长分别为4,8,则它的周长为( )
A.12 B.16 C.20 D.16或20
7.Rt△ABC中,∠C=90°,∠B=54°,则∠A的度数是( )
A.66° B.36° C.56 D.46°
8.如图,在△ABC中,∠C=90°,∠A=30°,若AB=6,则BC为( )
A.2 B.3 C.6 D.8
9.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为2.6km,则M,C两点间的距离为( )
A.0.8km B.1.2km C.1.3km D.5.2km
10.如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=10m,则A,B之间的距离是( )
A.5m B.10m C.20m D.40m
11.已知等边△ABC的边长是6,则它的周长是( )
A.6 B.12 C.18 D.3
12.已知△ABC∽△DEF,若△ABC与△DEF的相似比为1:3,则△ABC与△DEF的周长比为( )
A.1:2 B.1:3 C.1:4 D.1:9
13.已知△ABC∽△DEF,若周长比为4:9,则AC:DF= .
14.如图,在 ABCD中,对角线AC、BD相交于O,若BD=10,则OB= .
15.在平行四边形ABCD中,若∠A=38°,则∠C= .
16.如图,矩形ABCD中,对角线AC,BD相交于点O,OA=4,则BD= .
17.如图,在菱形ABCD中,对角线AC=12,BD=16,则这个菱形的周长为 .
18.正方形的边长为,则这个正方形的对角线长为 .
19.如图,在△ADC与△BDC中,∠1=∠2,加上条件 (只填写一个即可),则有△ADC≌△BDC.
20.若△ABC∽△A′B′C′,∠A=50°,∠C=110°,则∠B′的度数为 .
21.已知:如图,OA=OD,OB=OC.求证:△OAB≌△ODC.
22.已知,如图,AB=AD,∠B=∠D,∠1=∠2=60°.
(1)求证:△ADE≌△ABC;
(2)求证:AE=CE.
23.已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE.
24.如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且∠ABD=∠ACD,∠EAD=∠BAC.
(1)求证:AE=AD;
(2)若∠ACB=65°,求∠BDC的度数.
参考答案
1.解:A、因为4+4<9,所以本组数不能构成三角形.故本选项错误;
B、因为2+6=8,所以本组数不能构成三角形.故本选项错误;
C、因为3+4>5,所以本组数可以构成三角形.故本选项正确;
D、因为1+2=3,所以本组数不能构成三角形.故本选项错误;
故选:C.
2.解:A、12+22=5≠32,故不能组成直角三角形,错误;
B、22+32=13≠42,故不能组成直角三角形,错误;
C、42+52=41≠62,故不能组成直角三角形,错误;
D、52+122=169=132,故能组成直角三角形,正确.
故选:D.
3.解:∠1=130°﹣60°=70°,
故选:D.
4.解:△ABC的高AD是过顶点A与BC垂直的线段,只有D选项符合.
故选:D.
5.解:如图,由三角形内角和定理得到:∠2=180°﹣50°﹣72°=58°.
∵图中的两个三角形全等,
∴∠1=∠2=58°.
故选:D.
6.解:①当4为腰时,4+4=8,故此种情况不存在;
②当8为腰时,8﹣4<8<8+4,符合题意.
故此三角形的周长=8+8+4=20.
故选:C.
7.解:∵Rt△ABC中,∠C=90°,∠B=54°,
∴∠A=90°﹣∠B=90°﹣54°=36°;
故选:B.
8.解:∵在△ABC中,∠C=90°,∠A=30°,
∴BC=AB=×6=3,
故选:B.
9.解:在Rt△ACB中,点M是AB的中点,
∴CM=AB=×2.6=1.3(km),
故选:C.
10.解:∵点C,D分别是OA,OB的中点,
∴AB=2CD=20(m),
故选:C.
11.解:∵等边△ABC的边长是6,
∴它的周长是6×3=18.
故选:C.
12.解:∵△ABC∽△DEF,△ABC与△DEF的相似比为1:3,
∴△ABC与△DEF的周长比=,
故选:B.
13.解:∵△ABC∽△DEF,周长比为4:9,
∴△ABC与△DEF的相似比为4:9,即AC:DF=4:9,
故答案为:4:9
14.解:∵四边形ABCD是平行四边形,且BD=10,
∴BO=BD=5,
故答案为:5.
15.解:∵四边形ABCD是平行四边形,
∴∠A=∠C,
∵∠A=38°,
∴∠C=38°,
故答案为:38°.
16.解:∵四边形ABCD是矩形,
∴OA=OC=AC,BO=DO=BD,AC=BD,
∴BD=2OA=8,
故答案为:8.
17.解:∵四边形ABCD是菱形,
∴OA=AC=×12=6,OB=BD=×16=8,AC⊥BD,
∴AB===10.
∴此菱形的边长为10,
∴周长为40.
故答案为:40.
18.解:如图,连接AC,
∵四边形ABCD是正方形,
∴AB=BC=,∠B=90°,
∴AC=AB=2,
故答案为:2.
19.解:加上条件AD=BD(答案不唯一),则有△ADC≌△BDC.
理由是:
在△ADC和△BDC中,
,
∴△ADC≌△BDC(SAS),
故答案为:AD=BD(答案不唯一).
20.解:∵∠A=50°,∠C=110°,
∴∠B=180°﹣50°﹣110°=20°,
∵△ABC∽△A′B′C′,
∴∠B′=∠B=20°.
故答案为20°.
21.证明:在△OAB和△ODC中
,
∴△OAB≌△ODC(SAS).
22.(1)证明:∵∠1=∠2,
∴∠1+∠BAE=∠2+∠BAE,
即∠DAE=∠BAC,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(ASA);
(2)证明:由(1)得△ABC≌△ADE,
∴AE=AC,
∵∠2=60°,
∴△ACE是等边三角形,
∴AE=CE.
23.证明:∵AC∥DE,
∴∠ACB=∠E,∠ACD=∠D,
∵∠ACD=∠B,
∴∠D=∠B,
在△ABC和△EDC中,
∴△ABC≌△CDE(AAS).
24.证明:(1)∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中
,
∴△ABE≌△ACD(ASA),
∴AE=AD;
(2)解:∵∠ACB=65°,AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
∵∠ABD=∠ACD,∠AOB=∠COD,
∴∠BDC=∠BAC=50°.
