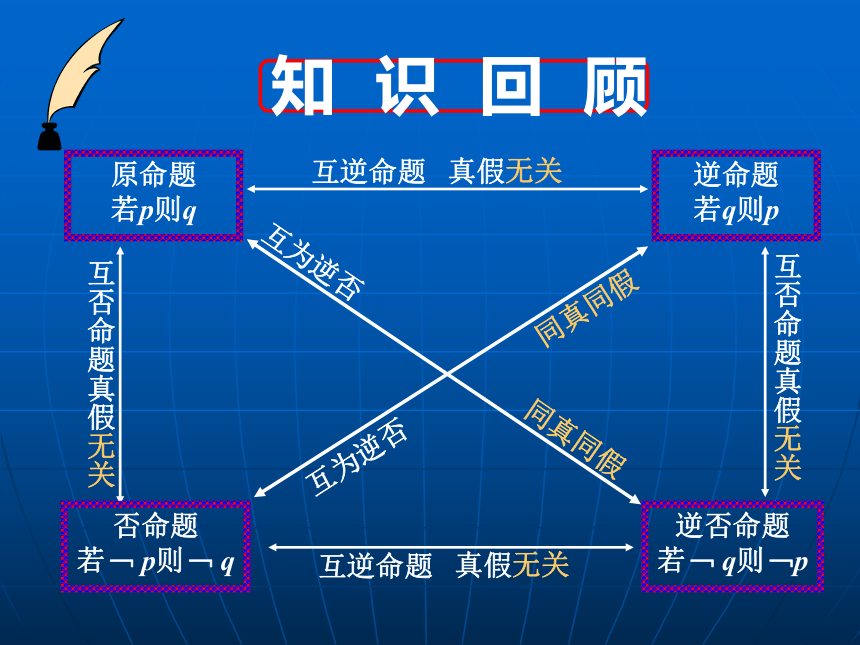
充分条件与必要条件
图片预览










文档简介
课件35张PPT。选修2-1第一章
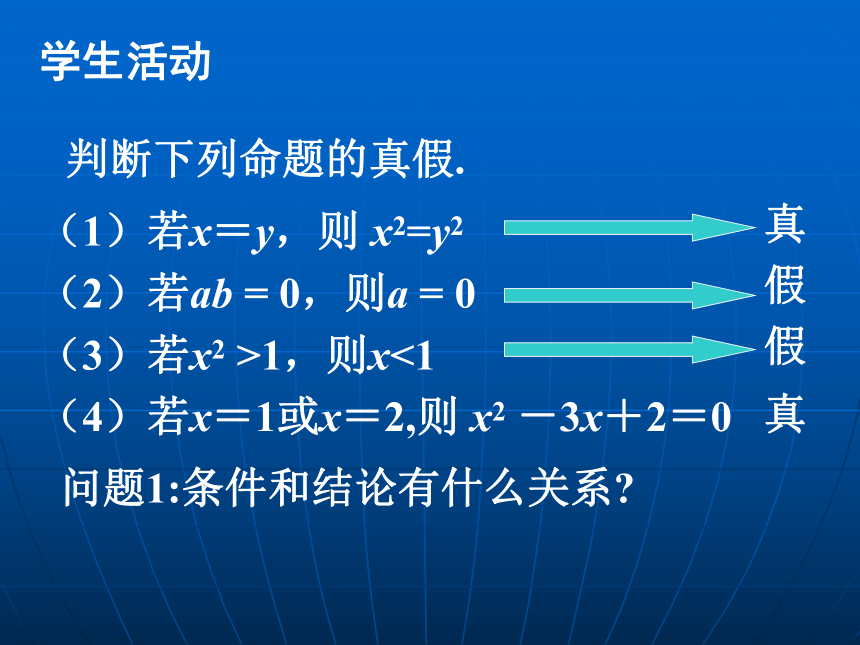
常用逻辑用语1.2充分条件与必要条件 (共两课时)学生活动判断下列命题的真假.(1)若x=y,则 x2=y2
(2)若ab = 0,则a = 0
(3)若x2 >1,则x<1
(4)若x=1或x=2,则 x2 -3x+2=0问题1:条件和结论有什么关系?真假假真 a = 0 ab = 0 问题1:说明条件和结论有什么关系? (1)x=y x2=y2(2)ab = 0 a = 0(3)x2>1 x<1(4)x=1或x=2 x2-3x+2=0x<1 x2>1x2-3x+2=0 x=1或x=2x2=y2 x=y ;;;; 新课概念 :定义一、充分条件与必要条件一般地, “若p,则q” 为真命题,
是指由p经过推理能推出q,
也就是说,如果p成立,那么q一定成立.
即:只要有p就能充分地保证q的成立,
这时我们说p可推出q, 我们就说p是q的充分条件;q是p必要条件. 如何理解充分条件
和必要条件? 上述定义知“ ”表示有p必有q,所以p是q的充分条件,但同时说q是p的必要条件是为什么呢?理解概念q是p的必要条件说明没有q就没有p了, q是 p成立的必不可少条件,当然有q 未必一定有p.这时逆否命题:¬q,则¬P.是真命题!即:“有p就有q”,那么“无q必定无p”,q对p而言是必不可少的! 充分性:条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证结论成立的。
“有之必成立,无之未必不成立” 理解概念必要性:必要就是必须,必不可少。
“有之未必成立,无之必不成立”你能举例说明吗?生活中有吗?你能举例说明吗?生活中有吗?若张三是高中生,则张三是中学生。 从集合角度理解:P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。二、充要条件一般地,如果既有p?q ,又有q?p 就记作
p ? q.
此时,我们说,那么p是q的充分必要条件,简称充要条件.
显然,如果p是q的充要条件,那么q也是p的充要条件.
即:如果p ? q,那么p 与 q互为充要条件.一般地,
若p?q ,但 q ?? p,则称p是q的充分但不必要条件;
若p??q,但q ? p,则称p是q的必要但不充分条件;
若p??q,且q ?? p,则称p是q的既不充分也不必要条件.例题1.下列“若p,则q”形式的命题中,哪些命题p是q的充分条件?
(1)若x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)在(-∞,+∞)上为增函数;
(3)若x为无理数,则x2为无理数.数学运用点拨:事实上就是判断“p ? q”是否为真命题。如(1)中“x=1” ? “x2-4x+3=0”,所以“x=1” 是 “x2-4x+3=0”的充分条件,但不可反推,故“x=1” 是 “x2-4x+3=0”的充分非必要条件.例题2.下列“若p,则q”形式的命题中,哪些命题 q是p的必要条件?
(1)若x=y,则x2=y2;
(2)若两三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc.点拨:还是判断“p ? q”是否为真命题。(1)x=y是x2=y2的_____________ 条件
(2)ab = 0是a = 0 的________________条件
(3)x2>1是x<1的__________________条件
(4)x=1或x=2是x2-3x+2=0的_____条件充分不必要必要不充分既不充分又不必要充要例题3.填空题,试用适当的词语填空例题4:指出下列各组命题中,p是q的什么条件:
(1) p:x-1=0;q:(x-1)(x+2)=0.
(2) p:两条直线平行;q:内错角相等.
(3) p:a>b;q:a2>b2
(4) p:四边形的四条边相等;
q:四边形是正四边形. 数学运用(1)充分不必要条件(2)充要条件(3)既不充分又不必要条件(4)必要不充分条件①“a和b都是偶数”是“a+b为偶数”的__条件;
②“x>5”是“x>3”的 条件;
③“x≠3”是“|x|≠3”的 条件;
④“个位数字是5的自然数”是“这个自然数能被5整除”的 条件;
⑤“至少有一组对应边相等”是“两个三角形全等”的 条件;课内活动运用本节课所讲的知识填空答案:(1)充分非必要(2)充分非必要(3)必要非充分(4)充分非必要(5)必要非充分思维活动——想一想1.给出一个命题p,能否写出它的多个充分条件?这些充分条件一定有因果关系吗?2.给出一个命题p,能否写出它的多个必要条件?这些必要条件一定有因果关系吗?——不一定有因果关系!——不一定有因果关系!素质拓展与学科渗透 现规定电路中,记“开关K 闭合”为p,“灯泡L 点亮”为q,指出下列各电路图中p是q的什么条件?p 是q 的
充要条件p 是q 的
必要而不
充分条件p 是q 的
充分而不
必要条件p 是q 的既
不充分也不
必要条件A课堂小结1.充分条件p是q的充分条件p ? q这时q是p的必要条件!2.必要条件p是q的必要条件q ? p这时 q是p的充分条件!Enjoy Maths,Enjoy Life!
享受数学,享受生活!选修2-1第一章 常用逻辑用语1.2充分条件与必要条件 (第二课时)一、复习回顾1.充分条件
若p?q , 则称p是q的充分条件;2.必要条件
若p?q , 则称q是 p的必要条件;3.充要条件
若p ? q,则称p是q的充要条件.命题“若p,则q”为真.若p?q ,但q ?? p,则称p是q的充分但不必要条件;
若p??q,但q ? p,则称p是q的必要但不充分条件;
若p??q,且q ?? p,则称p是q的既不充分也不必要条件.一般说法:命题“若p,则q”为真,命题 “若q,则p” 为假二、概念理解注意下列说法:1.若p是q的充分条件,那么q是p的必要条件;这时p?q成立(是真命题)2.若p是q的必要条件,那么q是p的充分条件;这时q ? p成立(是真命题)举例说明!比较下列说法:这时p?q成立q ? pq ? pq ? p哪个是条件?判断p是q的什么条件的步骤① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判断的常用技巧三、问题再现1.x>2是“x>3”的( )条件?
A.充分非必要条件;B.必要非充分条件;
C.充要条件;D.既非充分也非必要条件. B2.下列哪个条件是x>5成立的必要条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.A点评:若“x>a”是“x>b”的充分条件,则a≥b.
“大于一个较大的数则必大于一个较小的数”提示:x>3? x>2提示:x>5? ?(1)下列哪个条件是x>5成立的必要条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.(2)下列哪个条件是x>5成立的充分条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.比较下列说法:(3) x>5成立的必要条件是?( )
A.x>1; B.x>8; A提示: ? ? x>5提示:x>5? ?BA谁是条件?谁是结论?谁是条件?谁是结论?三、问题再现2.判断下列说法哪些是正确的?
(1)x=2是x2-3x+2=0的必要条件;
(2) x=2的一个必要条件是x2-3x+2=0 ;
(3) x2-3x+2=0的一个充分条件是x=2;
(4) x2-3x+2≠0的一个充分条件是x≠2.三、问题再现3.p是r的充分条件,s是r的必要条件,q是s的必要条件,那么q是p成立的( )
A.充分条件; B.必要条件;
C.充要条件; D.既非充分也非必要条件. 提示1:p ? r提示2:r? s提示3:s ? qp ? qB四、问题探讨例题1.下列各题中,哪些p是q的充要条件?(1)p: b=0, q: f(x)=ax2+bx+c是偶函数;
(2)p: x>0,y>0, q: xy>0;
(3)p: a>b, q: a+c>b+c.例2:已知:⊙O的半径为r,圆心O到直线l的距离为d.求证:d=r是直线l与⊙O相切的充要条件.分析:设p: d=r, q: l与⊙O相切.先证明充分性:p ? q再证明必要性:q ? p点拨:此类问题应注意充分性和必要性的条件练习:在△ABC中,三个角A、B、C所对的三边分别为a、b、c,求证:a>b>c的充要条件是A>B>C.注意:充分性是用哪个作条件?比较:
“a>b>c的充要条件是A>B>C.”
“a>b>c是A>B>C充要条件.”相同吗?五、充要条件的应用例3、已知:p:x2-8x-20≤0,q: x2-2x+1-m2≤0(m>0). ¬p是 ¬q的充分非必要条件,求实数m的取值范围.关键1.解出
p:-2≤x≤10,q:1-m≤x≤1+m;关键2. ¬p ? ¬q,即q?p关键3.设p、q的解集分别为A、B,则A、B的关系是B A六、课内练习教材P12-1、21.理解充分非必要条件和必要非充分条件;
2.理解两种说法:
“p是q的××条件”与“p成立的××条件是q”
3.初步掌握如何证明“充分性”、“必要性”七、小结Enjoy Maths,Enjoy Life!
享受数学,享受生活!
(2)若ab = 0,则a = 0
(3)若x2 >1,则x<1
(4)若x=1或x=2,则 x2 -3x+2=0问题1:条件和结论有什么关系?真假假真 a = 0 ab = 0 问题1:说明条件和结论有什么关系? (1)x=y x2=y2(2)ab = 0 a = 0(3)x2>1 x<1(4)x=1或x=2 x2-3x+2=0x<1 x2>1x2-3x+2=0 x=1或x=2x2=y2 x=y ;;;; 新课概念 :定义一、充分条件与必要条件一般地, “若p,则q” 为真命题,
是指由p经过推理能推出q,
也就是说,如果p成立,那么q一定成立.
即:只要有p就能充分地保证q的成立,
这时我们说p可推出q, 我们就说p是q的充分条件;q是p必要条件. 如何理解充分条件
和必要条件? 上述定义知“ ”表示有p必有q,所以p是q的充分条件,但同时说q是p的必要条件是为什么呢?理解概念q是p的必要条件说明没有q就没有p了, q是 p成立的必不可少条件,当然有q 未必一定有p.这时逆否命题:¬q,则¬P.是真命题!即:“有p就有q”,那么“无q必定无p”,q对p而言是必不可少的! 充分性:条件是充分的,也就是说条件是充足的,条件是足够的,条件是足以保证结论成立的。
“有之必成立,无之未必不成立” 理解概念必要性:必要就是必须,必不可少。
“有之未必成立,无之必不成立”你能举例说明吗?生活中有吗?你能举例说明吗?生活中有吗?若张三是高中生,则张三是中学生。 从集合角度理解:P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提。二、充要条件一般地,如果既有p?q ,又有q?p 就记作
p ? q.
此时,我们说,那么p是q的充分必要条件,简称充要条件.
显然,如果p是q的充要条件,那么q也是p的充要条件.
即:如果p ? q,那么p 与 q互为充要条件.一般地,
若p?q ,但 q ?? p,则称p是q的充分但不必要条件;
若p??q,但q ? p,则称p是q的必要但不充分条件;
若p??q,且q ?? p,则称p是q的既不充分也不必要条件.例题1.下列“若p,则q”形式的命题中,哪些命题p是q的充分条件?
(1)若x=1,则x2-4x+3=0;
(2)若f(x)=x,则f(x)在(-∞,+∞)上为增函数;
(3)若x为无理数,则x2为无理数.数学运用点拨:事实上就是判断“p ? q”是否为真命题。如(1)中“x=1” ? “x2-4x+3=0”,所以“x=1” 是 “x2-4x+3=0”的充分条件,但不可反推,故“x=1” 是 “x2-4x+3=0”的充分非必要条件.例题2.下列“若p,则q”形式的命题中,哪些命题 q是p的必要条件?
(1)若x=y,则x2=y2;
(2)若两三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc.点拨:还是判断“p ? q”是否为真命题。(1)x=y是x2=y2的_____________ 条件
(2)ab = 0是a = 0 的________________条件
(3)x2>1是x<1的__________________条件
(4)x=1或x=2是x2-3x+2=0的_____条件充分不必要必要不充分既不充分又不必要充要例题3.填空题,试用适当的词语填空例题4:指出下列各组命题中,p是q的什么条件:
(1) p:x-1=0;q:(x-1)(x+2)=0.
(2) p:两条直线平行;q:内错角相等.
(3) p:a>b;q:a2>b2
(4) p:四边形的四条边相等;
q:四边形是正四边形. 数学运用(1)充分不必要条件(2)充要条件(3)既不充分又不必要条件(4)必要不充分条件①“a和b都是偶数”是“a+b为偶数”的__条件;
②“x>5”是“x>3”的 条件;
③“x≠3”是“|x|≠3”的 条件;
④“个位数字是5的自然数”是“这个自然数能被5整除”的 条件;
⑤“至少有一组对应边相等”是“两个三角形全等”的 条件;课内活动运用本节课所讲的知识填空答案:(1)充分非必要(2)充分非必要(3)必要非充分(4)充分非必要(5)必要非充分思维活动——想一想1.给出一个命题p,能否写出它的多个充分条件?这些充分条件一定有因果关系吗?2.给出一个命题p,能否写出它的多个必要条件?这些必要条件一定有因果关系吗?——不一定有因果关系!——不一定有因果关系!素质拓展与学科渗透 现规定电路中,记“开关K 闭合”为p,“灯泡L 点亮”为q,指出下列各电路图中p是q的什么条件?p 是q 的
充要条件p 是q 的
必要而不
充分条件p 是q 的
充分而不
必要条件p 是q 的既
不充分也不
必要条件A课堂小结1.充分条件p是q的充分条件p ? q这时q是p的必要条件!2.必要条件p是q的必要条件q ? p这时 q是p的充分条件!Enjoy Maths,Enjoy Life!
享受数学,享受生活!选修2-1第一章 常用逻辑用语1.2充分条件与必要条件 (第二课时)一、复习回顾1.充分条件
若p?q , 则称p是q的充分条件;2.必要条件
若p?q , 则称q是 p的必要条件;3.充要条件
若p ? q,则称p是q的充要条件.命题“若p,则q”为真.若p?q ,但q ?? p,则称p是q的充分但不必要条件;
若p??q,但q ? p,则称p是q的必要但不充分条件;
若p??q,且q ?? p,则称p是q的既不充分也不必要条件.一般说法:命题“若p,则q”为真,命题 “若q,则p” 为假二、概念理解注意下列说法:1.若p是q的充分条件,那么q是p的必要条件;这时p?q成立(是真命题)2.若p是q的必要条件,那么q是p的充分条件;这时q ? p成立(是真命题)举例说明!比较下列说法:这时p?q成立q ? pq ? pq ? p哪个是条件?判断p是q的什么条件的步骤① 认清条件和结论。① 可先简化命题。③ 将命题转化为等价的逆否命题后再判断。② 否定一个命题只要举出一个反例即可。判断的常用技巧三、问题再现1.x>2是“x>3”的( )条件?
A.充分非必要条件;B.必要非充分条件;
C.充要条件;D.既非充分也非必要条件. B2.下列哪个条件是x>5成立的必要条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.A点评:若“x>a”是“x>b”的充分条件,则a≥b.
“大于一个较大的数则必大于一个较小的数”提示:x>3? x>2提示:x>5? ?(1)下列哪个条件是x>5成立的必要条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.(2)下列哪个条件是x>5成立的充分条件?( )
A.x>1; B.x>8;
C.x<5; D.x<6.比较下列说法:(3) x>5成立的必要条件是?( )
A.x>1; B.x>8; A提示: ? ? x>5提示:x>5? ?BA谁是条件?谁是结论?谁是条件?谁是结论?三、问题再现2.判断下列说法哪些是正确的?
(1)x=2是x2-3x+2=0的必要条件;
(2) x=2的一个必要条件是x2-3x+2=0 ;
(3) x2-3x+2=0的一个充分条件是x=2;
(4) x2-3x+2≠0的一个充分条件是x≠2.三、问题再现3.p是r的充分条件,s是r的必要条件,q是s的必要条件,那么q是p成立的( )
A.充分条件; B.必要条件;
C.充要条件; D.既非充分也非必要条件. 提示1:p ? r提示2:r? s提示3:s ? qp ? qB四、问题探讨例题1.下列各题中,哪些p是q的充要条件?(1)p: b=0, q: f(x)=ax2+bx+c是偶函数;
(2)p: x>0,y>0, q: xy>0;
(3)p: a>b, q: a+c>b+c.例2:已知:⊙O的半径为r,圆心O到直线l的距离为d.求证:d=r是直线l与⊙O相切的充要条件.分析:设p: d=r, q: l与⊙O相切.先证明充分性:p ? q再证明必要性:q ? p点拨:此类问题应注意充分性和必要性的条件练习:在△ABC中,三个角A、B、C所对的三边分别为a、b、c,求证:a>b>c的充要条件是A>B>C.注意:充分性是用哪个作条件?比较:
“a>b>c的充要条件是A>B>C.”
“a>b>c是A>B>C充要条件.”相同吗?五、充要条件的应用例3、已知:p:x2-8x-20≤0,q: x2-2x+1-m2≤0(m>0). ¬p是 ¬q的充分非必要条件,求实数m的取值范围.关键1.解出
p:-2≤x≤10,q:1-m≤x≤1+m;关键2. ¬p ? ¬q,即q?p关键3.设p、q的解集分别为A、B,则A、B的关系是B A六、课内练习教材P12-1、21.理解充分非必要条件和必要非充分条件;
2.理解两种说法:
“p是q的××条件”与“p成立的××条件是q”
3.初步掌握如何证明“充分性”、“必要性”七、小结Enjoy Maths,Enjoy Life!
享受数学,享受生活!
