直线的点斜式方程
图片预览










文档简介
课件38张PPT。给定直线l上的两点, P1(x1,y1)、P2(x2,y2),
则该直线l的斜率为:
一、温故而知新K=(2) 直线的斜率与倾斜角之间有什么关系?K=tan斜率k存在,即:x1 x23.2 直线的方程第三章 直线与方程 3.2.1 直线的点斜式方程问题1:过点P(-1,3)的直线有多少条? 问题2:过点P(-1,3)且倾斜角为 的直线有 多少条二:问题的提出如果直线l上一点B的横坐标为2,你能求出它的纵坐标吗?
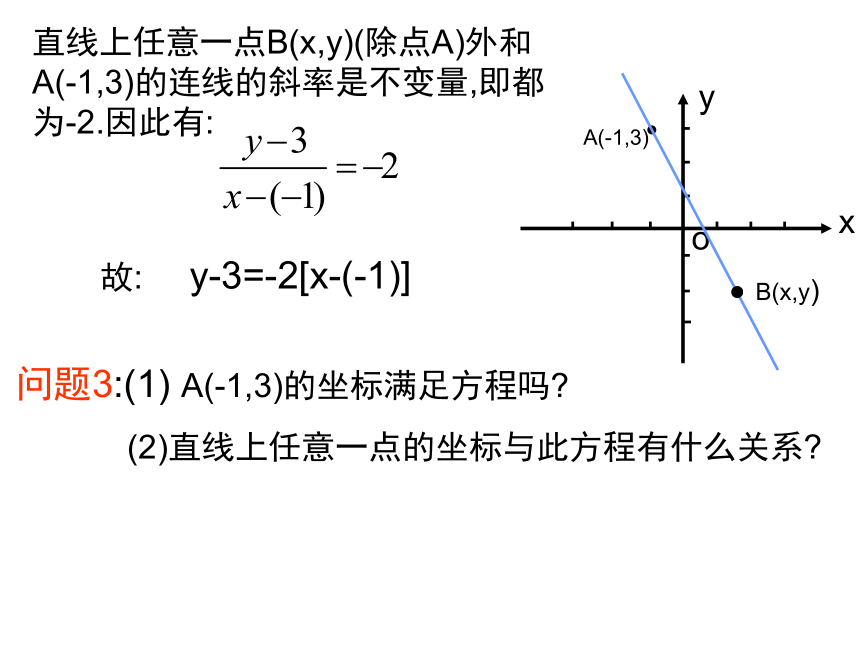
如果直线上一点B的横坐标为x,你能求出它的纵坐标吗?问题的探究:, 给定一个定点A(-1,3)和斜率为-2就可以决定一条直线l .B(2,-3)B(x,y)直线上任意一点B(x,y)(除点A)外和A(-1,3)的连线的斜率是不变量,即都为-2.因此有:故: y-3=-2[x-(-1)]问题3:(1) A(-1,3)的坐标满足方程吗?
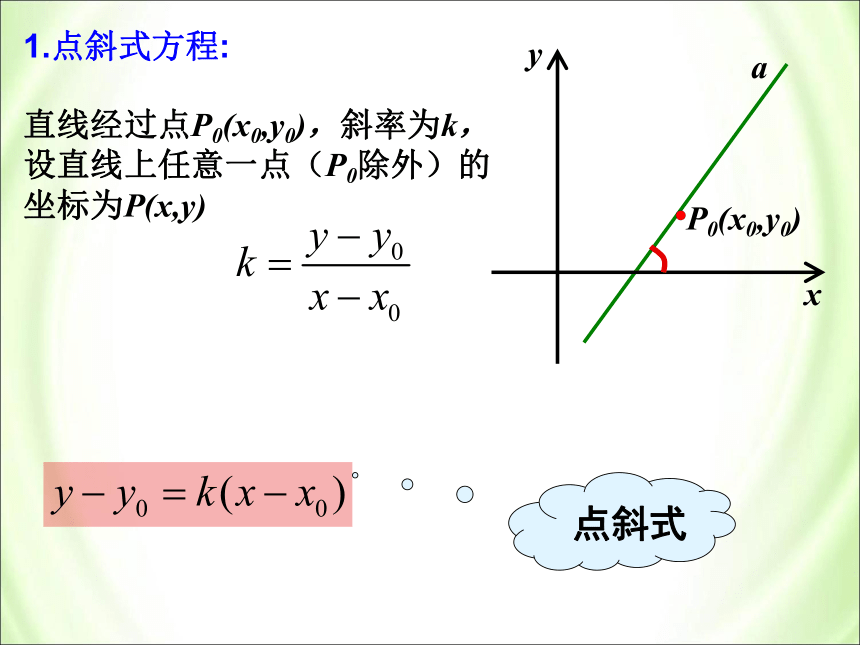
(2)直线上任意一点的坐标与此方程有什么关系?当点P(x,y)(不同于点 ) 在直线l上运动时, 的斜率恒等于k,即 故1.点斜式方程:xyaP0(x0,y0)直线经过点P0(x0,y0),斜率为k,设直线上任意一点(P0除外)的坐标为P(x,y)点斜式 (1)过点 ,斜率是 的直线 上的点,其坐标都满足方程 吗? (2)坐标满足方程 的点都在过点 斜率为 的直线 上吗? 上述两条都成立,所以这个方程
就是过点 斜率为 的直线 的方程.点斜式方程思考?,或的方程就是(1)与 轴平行或重合的直线的方程是什么?思考? 当直线 的倾斜角为 时,即 .
这时直线 与 轴平行或重合, (2)与 轴平行或重合的直线的方程是什么?,或 当直线 的倾斜角为 时,直线没有斜率,这时,直线 与 轴平行或重合,它的方程不能用点斜式表示.这时,直线 上每一点的横坐标都等于 ,所以它的方程就是思考?应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这
条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 0Oxy-55°P1°°应用:变式:一条直线经过点A(0,5),倾斜角为00,求这直线方程解:这条直线经过点A(0,5)
斜率是k=tan00=0代入点斜式,得y - 5 = 0Oxy5归纳:2.经过点P(x0,y0)的直线有无数 条,可分两类:1.点斜式的局限性:
只能表示斜率存在的直线
即不能表示与x轴垂直的直线练习:课本95页1,2创新52页斜截式方程:xyaP0(0,b)如果直线l斜率为k,且与y轴的交点为(0,b),则直线方程为斜率截距斜截式当知道斜率和直线在y轴的截距时用斜截式截距不是距离 我们把直线与 轴交点的纵坐标叫做直线在y轴上的截距。练习:课本95页3例题 例2 已知直线 , 试讨论:(1) 的条件是什么?(2) 的条件是什么? 解:,且 ;练习:课本95页4解 (1)∵直线的倾斜角为60°,
∴其斜率k=tan 60°= .
∵直线与y轴的交点到原点的距离为3,
∴直线在y轴上的截距b=3或b=-3.
∴所求直线方程为y= x+3或y= x-3.创新52页(2)由斜截式方程知直线l1的斜率k1=-2,
又∵l∥l1,∴l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
∴l在y轴上的截距b=-2,
由斜截式可得直线l的方程为y=-2x-2.创新53页创新53页课堂小结斜率k和直线在y轴上的截距活页规范训练2.已知直线的方程是y+2=-x-1,则( ).
A.直线经过点(-1,2),斜率为-1
B.直线经过点(2,-1),斜率为-1
C.直线经过点(-1,-2),斜率为-1
D.直线经过点(-2,-1),斜率为1
解析 直线的方程可化为y-(-2)=-[x-(-1)],故直线经过点(-1,-2),斜率为-1.
答案 C5.(2012·汕头高一检测)经过点(0,2),且与直线y=-3x-5平行的直线l的方程为________.
解析 由y=-3x-5得,其斜率k1=-3,
由两直线平行知,kl=k1=-3,
∴所求直线方程为y-2=-3x,
即y=-3x+2.
本题亦可设所求直线方程为y=-3x+c将点(0,2)代入求c.
答案 y=-3x+27.(2012·镇海高一检测)经过点(-1,1),斜率是直线y= x-2的斜率的2倍的直线方程是( ).
A.x=-1 B.y=1
C.y-1= (x+1) D.y-1=2 (x+1)
解析 由方程知,已知直线的斜率为 ,
∴所求直线的斜率是 ,由直线方程的点斜式可得方程为y-1= (x+1),∴选C.
答案 C8.已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( ).
解析 列表如下:
由上表排除A、B、D.故选C.9.直线l的方程为y-a=(a-1)(x+2),若直线l在y轴上的截距为6,则a=________.
解析 直线l的方程可化为y=(a-1)x+3a-2,由直线l在y轴上的截距为6可得:3a-2=6,
解得a= .
答案 10.在直线方程y=kx+b中,当x∈[-3,4]时,恰好y∈[-8,13],则此直线方程为________.
解析 方程y=kx+b,即一次函数y=kx+b,由一次函数单调性可知:
当k>0时,函数为增函数,
∴ 解之得 ;
当k<0时,函数为减函数,
∴ 解之得
答案 y=3x+1或y=-3x+412.(创新拓展)已知△ABC的三个顶点在第一象限,A(1,1),B(5,1),A=45°,B=45°,求:
(1)AB边所在直线的方程;
解 (1)由题意知,直线AB平行于x轴,
由A,B两点的坐标知,直线AB的方程为y=1.12.(创新拓展)已知△ABC的三个顶点在第一象限,A(1,1),B(5,1),A=45°,B=45°,求:
(2)AC边和BC边所在直线的方程.
解 (2)由题意知,直线AC的倾斜角等于A,
所以kAC=tan 45°=1,
又点A(1,1),
所以直线AC的方程为y-1=1×(x-1),即y=x.
同理,直线BC的倾斜角等于180°-B=135°,
所以kBC=tan 135°=-1,
又点B(5,1),
所以直线BC的方程为y-1=-1×(x-5),即y=-x+6.
加分题:直线kx-y+1-3k=0当k变化时,所有的直线恒过定点 ( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)答案:C
则该直线l的斜率为:
一、温故而知新K=(2) 直线的斜率与倾斜角之间有什么关系?K=tan斜率k存在,即:x1 x23.2 直线的方程第三章 直线与方程 3.2.1 直线的点斜式方程问题1:过点P(-1,3)的直线有多少条? 问题2:过点P(-1,3)且倾斜角为 的直线有 多少条二:问题的提出如果直线l上一点B的横坐标为2,你能求出它的纵坐标吗?
如果直线上一点B的横坐标为x,你能求出它的纵坐标吗?问题的探究:, 给定一个定点A(-1,3)和斜率为-2就可以决定一条直线l .B(2,-3)B(x,y)直线上任意一点B(x,y)(除点A)外和A(-1,3)的连线的斜率是不变量,即都为-2.因此有:故: y-3=-2[x-(-1)]问题3:(1) A(-1,3)的坐标满足方程吗?
(2)直线上任意一点的坐标与此方程有什么关系?当点P(x,y)(不同于点 ) 在直线l上运动时, 的斜率恒等于k,即 故1.点斜式方程:xyaP0(x0,y0)直线经过点P0(x0,y0),斜率为k,设直线上任意一点(P0除外)的坐标为P(x,y)点斜式 (1)过点 ,斜率是 的直线 上的点,其坐标都满足方程 吗? (2)坐标满足方程 的点都在过点 斜率为 的直线 上吗? 上述两条都成立,所以这个方程
就是过点 斜率为 的直线 的方程.点斜式方程思考?,或的方程就是(1)与 轴平行或重合的直线的方程是什么?思考? 当直线 的倾斜角为 时,即 .
这时直线 与 轴平行或重合, (2)与 轴平行或重合的直线的方程是什么?,或 当直线 的倾斜角为 时,直线没有斜率,这时,直线 与 轴平行或重合,它的方程不能用点斜式表示.这时,直线 上每一点的横坐标都等于 ,所以它的方程就是思考?应用:例1:一条直线经过点P1(-2,3),倾斜角α=450,求这
条直线的方程,并画出图形。解:这条直线经过点P1(-2,3),
斜率是 k=tan450=1代入点斜式得y-3 = x + 2, 即x-y + 5 = 0Oxy-55°P1°°应用:变式:一条直线经过点A(0,5),倾斜角为00,求这直线方程解:这条直线经过点A(0,5)
斜率是k=tan00=0代入点斜式,得y - 5 = 0Oxy5归纳:2.经过点P(x0,y0)的直线有无数 条,可分两类:1.点斜式的局限性:
只能表示斜率存在的直线
即不能表示与x轴垂直的直线练习:课本95页1,2创新52页斜截式方程:xyaP0(0,b)如果直线l斜率为k,且与y轴的交点为(0,b),则直线方程为斜率截距斜截式当知道斜率和直线在y轴的截距时用斜截式截距不是距离 我们把直线与 轴交点的纵坐标叫做直线在y轴上的截距。练习:课本95页3例题 例2 已知直线 , 试讨论:(1) 的条件是什么?(2) 的条件是什么? 解:,且 ;练习:课本95页4解 (1)∵直线的倾斜角为60°,
∴其斜率k=tan 60°= .
∵直线与y轴的交点到原点的距离为3,
∴直线在y轴上的截距b=3或b=-3.
∴所求直线方程为y= x+3或y= x-3.创新52页(2)由斜截式方程知直线l1的斜率k1=-2,
又∵l∥l1,∴l的斜率k=k1=-2.
由题意知l2在y轴上的截距为-2,
∴l在y轴上的截距b=-2,
由斜截式可得直线l的方程为y=-2x-2.创新53页创新53页课堂小结斜率k和直线在y轴上的截距活页规范训练2.已知直线的方程是y+2=-x-1,则( ).
A.直线经过点(-1,2),斜率为-1
B.直线经过点(2,-1),斜率为-1
C.直线经过点(-1,-2),斜率为-1
D.直线经过点(-2,-1),斜率为1
解析 直线的方程可化为y-(-2)=-[x-(-1)],故直线经过点(-1,-2),斜率为-1.
答案 C5.(2012·汕头高一检测)经过点(0,2),且与直线y=-3x-5平行的直线l的方程为________.
解析 由y=-3x-5得,其斜率k1=-3,
由两直线平行知,kl=k1=-3,
∴所求直线方程为y-2=-3x,
即y=-3x+2.
本题亦可设所求直线方程为y=-3x+c将点(0,2)代入求c.
答案 y=-3x+27.(2012·镇海高一检测)经过点(-1,1),斜率是直线y= x-2的斜率的2倍的直线方程是( ).
A.x=-1 B.y=1
C.y-1= (x+1) D.y-1=2 (x+1)
解析 由方程知,已知直线的斜率为 ,
∴所求直线的斜率是 ,由直线方程的点斜式可得方程为y-1= (x+1),∴选C.
答案 C8.已知直线l1:y=kx+b,l2:y=bx+k,则它们的图象可能为( ).
解析 列表如下:
由上表排除A、B、D.故选C.9.直线l的方程为y-a=(a-1)(x+2),若直线l在y轴上的截距为6,则a=________.
解析 直线l的方程可化为y=(a-1)x+3a-2,由直线l在y轴上的截距为6可得:3a-2=6,
解得a= .
答案 10.在直线方程y=kx+b中,当x∈[-3,4]时,恰好y∈[-8,13],则此直线方程为________.
解析 方程y=kx+b,即一次函数y=kx+b,由一次函数单调性可知:
当k>0时,函数为增函数,
∴ 解之得 ;
当k<0时,函数为减函数,
∴ 解之得
答案 y=3x+1或y=-3x+412.(创新拓展)已知△ABC的三个顶点在第一象限,A(1,1),B(5,1),A=45°,B=45°,求:
(1)AB边所在直线的方程;
解 (1)由题意知,直线AB平行于x轴,
由A,B两点的坐标知,直线AB的方程为y=1.12.(创新拓展)已知△ABC的三个顶点在第一象限,A(1,1),B(5,1),A=45°,B=45°,求:
(2)AC边和BC边所在直线的方程.
解 (2)由题意知,直线AC的倾斜角等于A,
所以kAC=tan 45°=1,
又点A(1,1),
所以直线AC的方程为y-1=1×(x-1),即y=x.
同理,直线BC的倾斜角等于180°-B=135°,
所以kBC=tan 135°=-1,
又点B(5,1),
所以直线BC的方程为y-1=-1×(x-5),即y=-x+6.
加分题:直线kx-y+1-3k=0当k变化时,所有的直线恒过定点 ( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)答案:C
