直线的一般式方程
图片预览







文档简介
课件20张PPT。3.2.3直线的一般式方程复习我们共学习了几种直线方程的形式?点斜式斜截式两点式截距式 过点 与x轴垂直的直线可表示成 , 过点 与y轴垂直的直线可表示成 。上述四种直线方程,能否写成如下统一形式?
? x+ ? y+ ? =0
上述四式都可以写成以下形式:
Ax+By+C=0, (A、B不同时为0)直线的一般式方程:,其中A,B不同时为0一般式①当B≠0时②当B=0时,是垂直于x轴的一条直线③当A=0时,是平行于x轴的一条直线直线的一般式方程:,其中A,B不同时为0一般式注意 对于直线方程的一般式,一般作如下约定:
1)x的系数为正,
2)x,y的系数及常数项一般不出现分数,
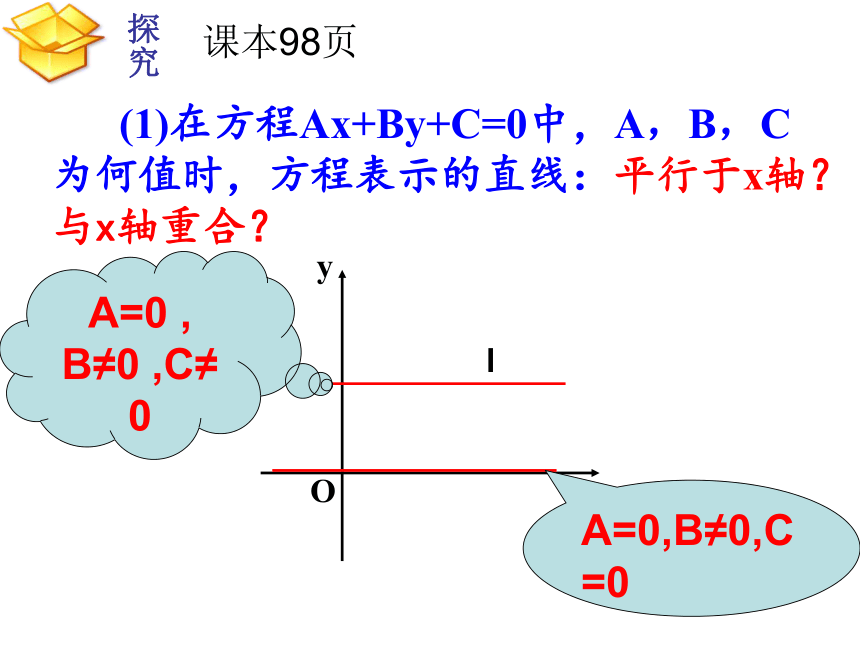
3)一般按含x项,含y项、常数项顺序排列. (1)在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:平行于x轴?与x轴重合? 探究A=0,B≠0,C=0
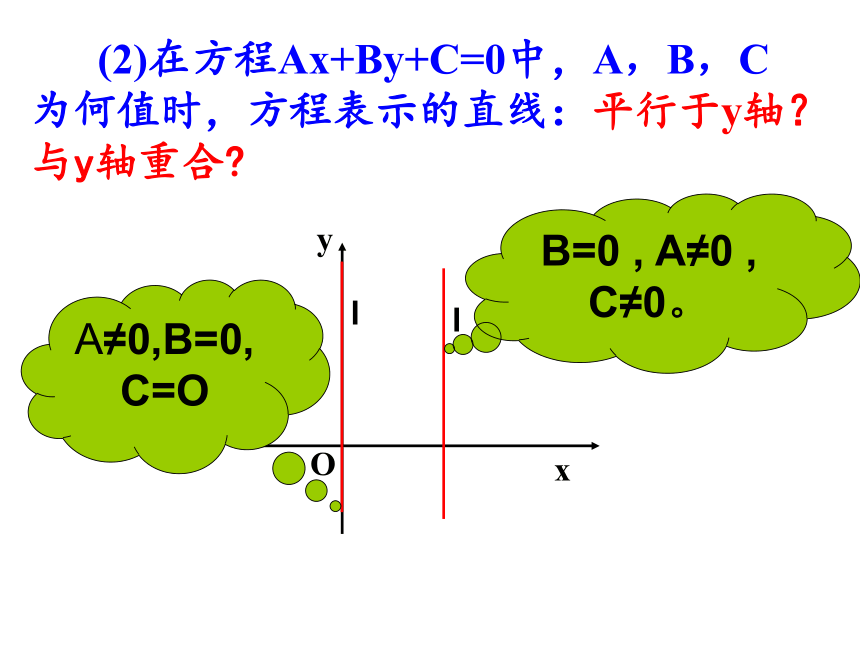
A=0 , B≠0 ,C≠0课本98页 (2)在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:平行于y轴?与y轴重合?B=0 , A≠0 , C≠0。A≠0,B=0,C=O 在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:过原点? 与x轴和y轴相交?C=0,A,B不同时为0。A≠0,B≠0例5:已知直线经过点A(6,-4),斜率
为-—,求直线的点斜式和一般式方程.34解:经过点A(6,-4),斜率为-—的点斜式方
程是: 34y+4= - —(x-6) 3 4化成一般式得: 4x+3y-12=0. 分析:因此直线的斜率为 例6:把直线的一般式方程x-2y+6=0化成斜
截式,求出直线的斜率以及它在x轴与y轴上
的截距,并画出图形.在y轴上的截距为3. 在x-2y+6=0中令y=0,有x= -6因此直线在x轴上的截距是-6.综上可知,直线与x轴、y轴的交
点为: A(-6,0),B(0,3)过A,B两点作直线,得到直线的图形.练习:课本99页1,2设直线l的斜率为k,(3分)
∵l与直线3x+4y+1=0平行,
∴k= .(8分)
又∵l经过点(1,2),可得所求直线方程为
y-2=-(x-1),即3x+4y-11=0.(12分)创新56页设直线l的斜率为k.(3分)
∵直线l与直线2x+y-10=0垂直,
∴k·(-2)=-1,∴k= .
又∵l经过点A(2,1),(8分)
∴所求直线l的方程为y-1=(x-2),即x-2y=0.(12分)活页规范训练3.直线l的方程为Ax+By+C=0,若l过原点和第二、四象限,则( ).
A.C=0,且B>0 B.C=0,B>0,A>0
C.C=0,AB<0 D.C=0,AB>0
解析 直线过原点,则C=0,
又过第二、四象限,所以斜率为负值,即k= <0,
∴AB>0,故选D.
答案 D5.直线(2-m)x+my+3=0与直线x-my-3=0垂直,则m为________.
解析 由直线方程可知,当一条直线的斜率不存在时,不存在m使两直线垂直,所以两直线的斜率都存在.
由k1·k2=-1,可得 =-1,解得m=-2或m=1.
答案 -2或16.求平行于直线3x+2y-6=0,且在两坐标轴上截距之和为-2的直线方程.
解 设所求直线的方程为3x+2y+λ=0,
令x=0,则y= ,令y=0,则x= ,
所以 =-2,解之得λ= .
所求直线方程为3x+2y+ =0,
即15x+10y+12=0.11.(2012·东北师大高一检测)已知两直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,当m为何值时,直线l1与l2:
(1)平行;(2)垂直.
解:当m=0时,l1:x+6=0,l2:2x-3y=0,l1与l2相交且不垂直;
当m≠0时,l1:y= ,l2:y = .
(1)l1∥l2?- =- 且- ≠- ,解得m=-1.
∴当m=-1时,l1∥l2.
(2)l1⊥l2? · =-1,解得m= .
∴当m= 时,l1⊥l2.
? x+ ? y+ ? =0
上述四式都可以写成以下形式:
Ax+By+C=0, (A、B不同时为0)直线的一般式方程:,其中A,B不同时为0一般式①当B≠0时②当B=0时,是垂直于x轴的一条直线③当A=0时,是平行于x轴的一条直线直线的一般式方程:,其中A,B不同时为0一般式注意 对于直线方程的一般式,一般作如下约定:
1)x的系数为正,
2)x,y的系数及常数项一般不出现分数,
3)一般按含x项,含y项、常数项顺序排列. (1)在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:平行于x轴?与x轴重合? 探究A=0,B≠0,C=0
A=0 , B≠0 ,C≠0课本98页 (2)在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:平行于y轴?与y轴重合?B=0 , A≠0 , C≠0。A≠0,B=0,C=O 在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线:过原点? 与x轴和y轴相交?C=0,A,B不同时为0。A≠0,B≠0例5:已知直线经过点A(6,-4),斜率
为-—,求直线的点斜式和一般式方程.34解:经过点A(6,-4),斜率为-—的点斜式方
程是: 34y+4= - —(x-6) 3 4化成一般式得: 4x+3y-12=0. 分析:因此直线的斜率为 例6:把直线的一般式方程x-2y+6=0化成斜
截式,求出直线的斜率以及它在x轴与y轴上
的截距,并画出图形.在y轴上的截距为3. 在x-2y+6=0中令y=0,有x= -6因此直线在x轴上的截距是-6.综上可知,直线与x轴、y轴的交
点为: A(-6,0),B(0,3)过A,B两点作直线,得到直线的图形.练习:课本99页1,2设直线l的斜率为k,(3分)
∵l与直线3x+4y+1=0平行,
∴k= .(8分)
又∵l经过点(1,2),可得所求直线方程为
y-2=-(x-1),即3x+4y-11=0.(12分)创新56页设直线l的斜率为k.(3分)
∵直线l与直线2x+y-10=0垂直,
∴k·(-2)=-1,∴k= .
又∵l经过点A(2,1),(8分)
∴所求直线l的方程为y-1=(x-2),即x-2y=0.(12分)活页规范训练3.直线l的方程为Ax+By+C=0,若l过原点和第二、四象限,则( ).
A.C=0,且B>0 B.C=0,B>0,A>0
C.C=0,AB<0 D.C=0,AB>0
解析 直线过原点,则C=0,
又过第二、四象限,所以斜率为负值,即k= <0,
∴AB>0,故选D.
答案 D5.直线(2-m)x+my+3=0与直线x-my-3=0垂直,则m为________.
解析 由直线方程可知,当一条直线的斜率不存在时,不存在m使两直线垂直,所以两直线的斜率都存在.
由k1·k2=-1,可得 =-1,解得m=-2或m=1.
答案 -2或16.求平行于直线3x+2y-6=0,且在两坐标轴上截距之和为-2的直线方程.
解 设所求直线的方程为3x+2y+λ=0,
令x=0,则y= ,令y=0,则x= ,
所以 =-2,解之得λ= .
所求直线方程为3x+2y+ =0,
即15x+10y+12=0.11.(2012·东北师大高一检测)已知两直线l1:x+my+6=0,l2:(m-2)x+3y+2m=0,当m为何值时,直线l1与l2:
(1)平行;(2)垂直.
解:当m=0时,l1:x+6=0,l2:2x-3y=0,l1与l2相交且不垂直;
当m≠0时,l1:y= ,l2:y = .
(1)l1∥l2?- =- 且- ≠- ,解得m=-1.
∴当m=-1时,l1∥l2.
(2)l1⊥l2? · =-1,解得m= .
∴当m= 时,l1⊥l2.
