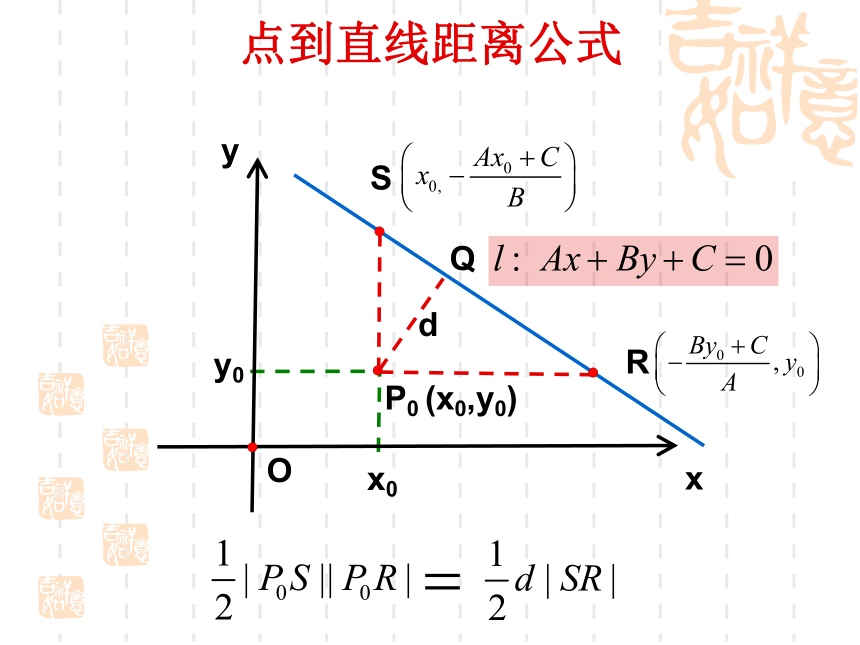
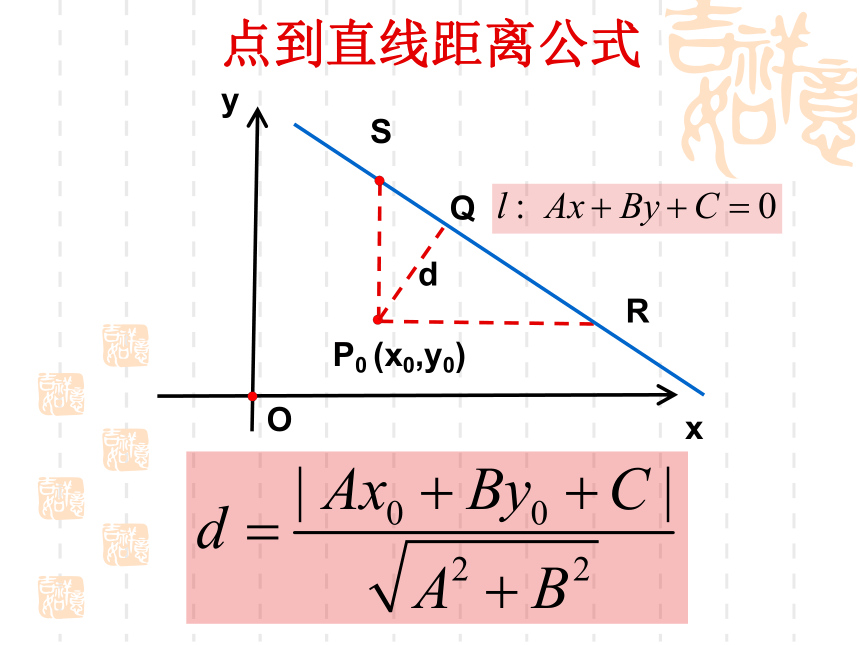
点到直线的距离
图片预览



文档简介
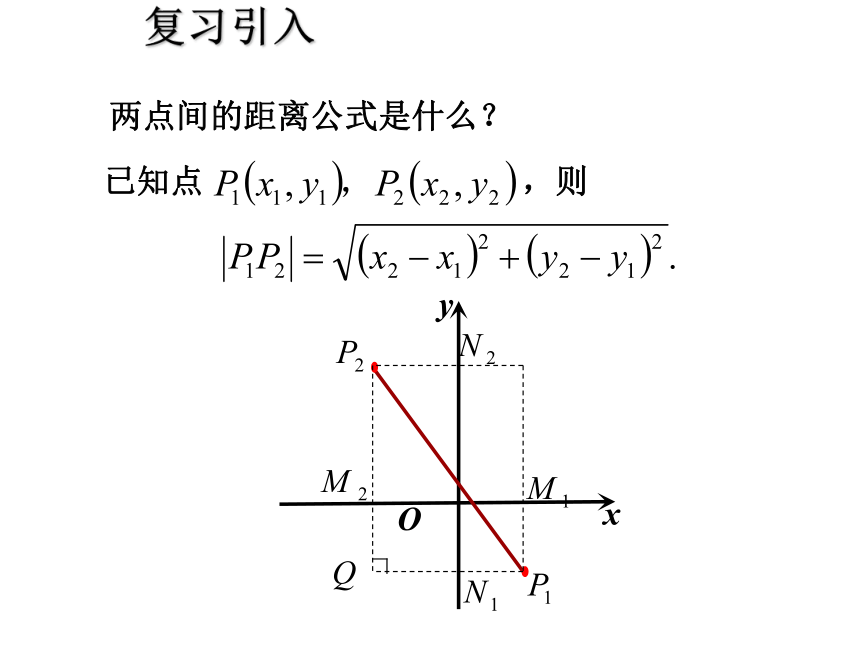
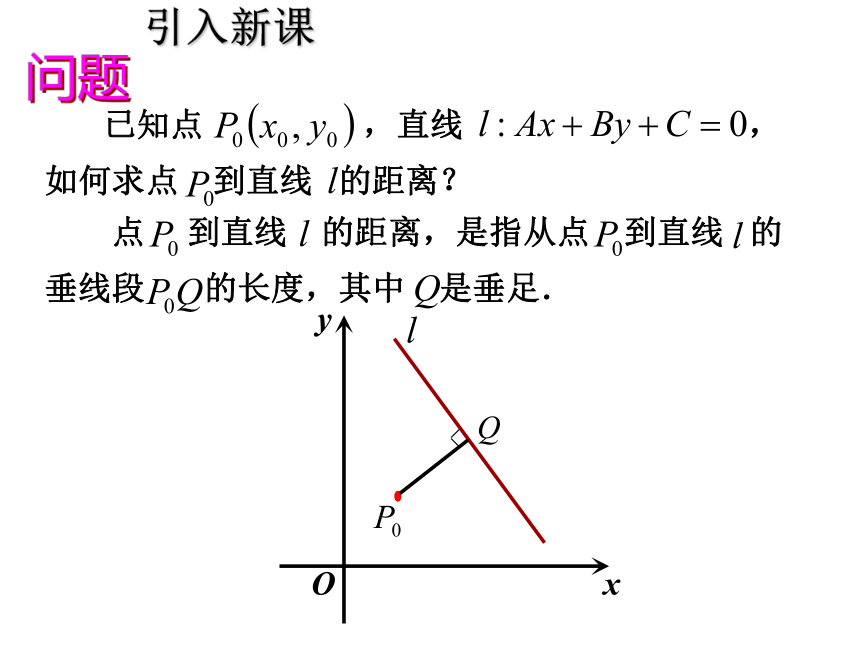
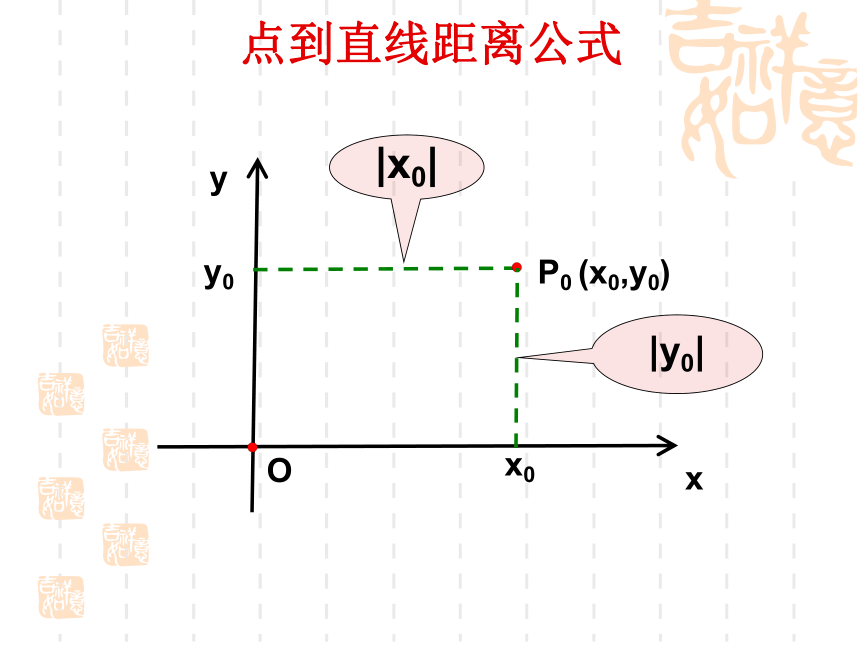
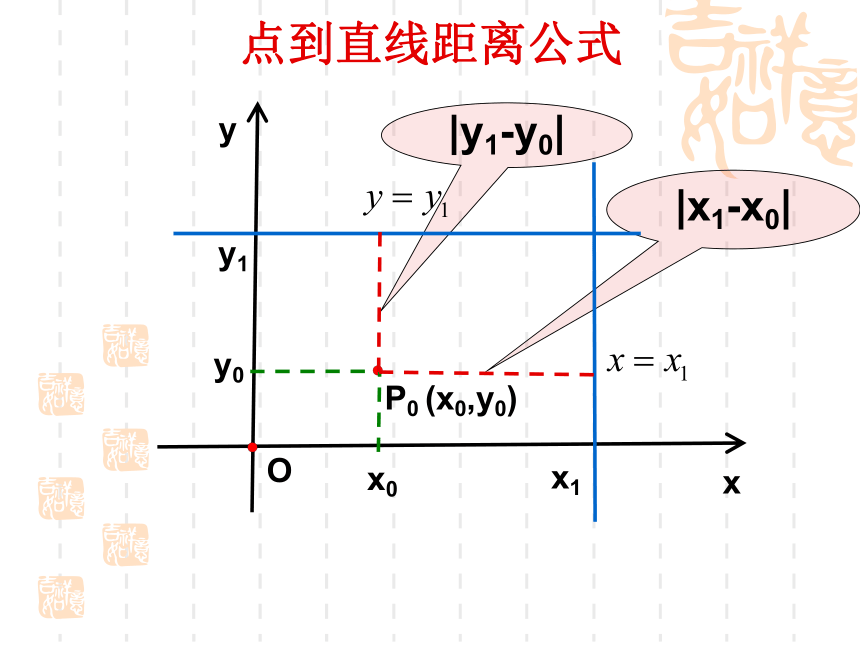
课件26张PPT。3.3.3 点到直线的距离两点间的距离公式是什么? 已知点 ,则xyO复习引入 已知点 ,直线 ,如何求点 到直线 的距离? 点 到直线 的距离,是指从点 到直线 的垂线段 的长度,其中 是垂足.xyO引入新课问题点到直线距离公式xyP0 (x0,y0)O|y0||x0|x0y0点到直线距离公式xyP0 (x0,y0)O|x1-x0||y1-y0|x0y0y1x1点到直线距离公式xyP0 (x0,y0)Ox0y0SRQd点到直线距离公式xyP0 (x0,y0)OSRQd1.此公式的作用是求点到直线的距离;2.此公式是在A、B≠0的前提下推导的;3.如果A=0或B=0,此公式恰好也成立;4.用此公式时直线要先化成一般式。d例5 求点P(-1,2)到直线①2x+y-10=0;
②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样??求下列点到直线的距离:(1)A(-2,3),l:3x+4y+3=0 (3)C(1,-2),l: 4x+3y=0 解:d= (1)d= =0(2)d= (3)课本108页 2课本108页 1 例6 已知点 ,求 的面积.解:如图,设 边上的高为 ,则xO-1123 边上的高 就是点 到 的距离.典型例题 边所在直线的方程为:即: 点 到 的距离因此,解: 例6 已知点 ,求 的面积.典型例题xO-1123创新61页例7 求平行线2x-7y+8=0与2x-7y-6=0的距离.两平行线间的距离处处相等在l2上任取一点,如P(3,0)P到l1的距离等于l1与l2的距离直线到直线的距离转化为点到直线的距离解:
PQ任意两条平行直线都可以写成如下形式:1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和3x+4y=0的距离是____.练习33.两平行线3x-2y-1=0和6x-4y+2=0的距离是____.2课本109页解 ∵与l平行的直线方程为5x-12y+b=0,
根据两平行直线间距离公式得 =3,
解之得c=45或c=-33,
所以所求直线方程为:5x-12y+45=0或5x-12y-33=0.创新61页活页规范训练2.(2012·淮阳高一检测)已知直线3x+2y-3=0和6x+my+1=0互相平行,则它们之间的距离是( ).
A.4 B. C. D.
解析 ∵3x+2y-3=0和6x+my+1=0互相平行,
∴3∶2=6∶m,∴m=4.
直线6x+4y+1=0可以化为3x+2y+ =0,由两条平行直线间的距离公式可得:
d= = = .
答案 D4.在过点A(2,1)的所有直线中,距离原点最远的直线方程为________.
解析 当直线l与OA垂直时,原点到直线l的距离最大,
∵kOA= ,∴kl=-2.
∴方程为y-1=-2(x-2),即2x+y-5=0.
答案 2x+y-5=05.已知直线l与直线l1:2x-y+3=0和l2:2x-y-1=0的距离相等,则l的方程是________.
解析 由题意可设l的方程为2x-y+c=0,
于是有 ,
即|c-3|=|c+1|.∴c=1,
∴直线l的方程为2x-y+1=0. 9.直线l在x轴上的截距为1,又有两点A(-2,-1),B(4,5)到l的距离相等,则l的方程为________.
解析 显然l⊥x轴时符合要求,此时l的方程为x=1;
设l的斜率为k,则l的方程为y=k(x-1),即kx-y-k=0,由于点A,B到l的距离相等.
∴ .
∴|1-3k|=|3k-5|,
∴k=1,∴l的方程为x-y-1=0.
答案 x-y-1=0,或x=110.若两平行线2x+y-4=0与y=-2x-k-2的距离不大于,则k的取值范围是________.
解析 化为一般式得,2x+y+k+2=0,
∴由平行线距离公式得:
0< ≤ ,
即0<|k+6|≤5,
∴-5≤k+6≤5且k+6≠0,
∴-11≤k≤-1且k≠-6.
答案 -11≤k≤-1且k≠-6
②3x=2的距离。解: ①根据点到直线的距离公式,得②如图,直线3x=2平行于y轴,用公式验证,结果怎样??求下列点到直线的距离:(1)A(-2,3),l:3x+4y+3=0 (3)C(1,-2),l: 4x+3y=0 解:d= (1)d= =0(2)d= (3)课本108页 2课本108页 1 例6 已知点 ,求 的面积.解:如图,设 边上的高为 ,则xO-1123 边上的高 就是点 到 的距离.典型例题 边所在直线的方程为:即: 点 到 的距离因此,解: 例6 已知点 ,求 的面积.典型例题xO-1123创新61页例7 求平行线2x-7y+8=0与2x-7y-6=0的距离.两平行线间的距离处处相等在l2上任取一点,如P(3,0)P到l1的距离等于l1与l2的距离直线到直线的距离转化为点到直线的距离解:
PQ任意两条平行直线都可以写成如下形式:1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和3x+4y=0的距离是____.练习33.两平行线3x-2y-1=0和6x-4y+2=0的距离是____.2课本109页解 ∵与l平行的直线方程为5x-12y+b=0,
根据两平行直线间距离公式得 =3,
解之得c=45或c=-33,
所以所求直线方程为:5x-12y+45=0或5x-12y-33=0.创新61页活页规范训练2.(2012·淮阳高一检测)已知直线3x+2y-3=0和6x+my+1=0互相平行,则它们之间的距离是( ).
A.4 B. C. D.
解析 ∵3x+2y-3=0和6x+my+1=0互相平行,
∴3∶2=6∶m,∴m=4.
直线6x+4y+1=0可以化为3x+2y+ =0,由两条平行直线间的距离公式可得:
d= = = .
答案 D4.在过点A(2,1)的所有直线中,距离原点最远的直线方程为________.
解析 当直线l与OA垂直时,原点到直线l的距离最大,
∵kOA= ,∴kl=-2.
∴方程为y-1=-2(x-2),即2x+y-5=0.
答案 2x+y-5=05.已知直线l与直线l1:2x-y+3=0和l2:2x-y-1=0的距离相等,则l的方程是________.
解析 由题意可设l的方程为2x-y+c=0,
于是有 ,
即|c-3|=|c+1|.∴c=1,
∴直线l的方程为2x-y+1=0. 9.直线l在x轴上的截距为1,又有两点A(-2,-1),B(4,5)到l的距离相等,则l的方程为________.
解析 显然l⊥x轴时符合要求,此时l的方程为x=1;
设l的斜率为k,则l的方程为y=k(x-1),即kx-y-k=0,由于点A,B到l的距离相等.
∴ .
∴|1-3k|=|3k-5|,
∴k=1,∴l的方程为x-y-1=0.
答案 x-y-1=0,或x=110.若两平行线2x+y-4=0与y=-2x-k-2的距离不大于,则k的取值范围是________.
解析 化为一般式得,2x+y+k+2=0,
∴由平行线距离公式得:
0< ≤ ,
即0<|k+6|≤5,
∴-5≤k+6≤5且k+6≠0,
∴-11≤k≤-1且k≠-6.
答案 -11≤k≤-1且k≠-6
