广西河池市2021-2022学年高三上学期期末物理模拟试卷(1)(Word版含答案)
文档属性
| 名称 | 广西河池市2021-2022学年高三上学期期末物理模拟试卷(1)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 601.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-06 14:24:52 | ||
图片预览



文档简介
2021-2022学年广西河池市高三(上)期末物理模拟试卷(1)
一.选择题(共8小题,满分48分,每小题6分)
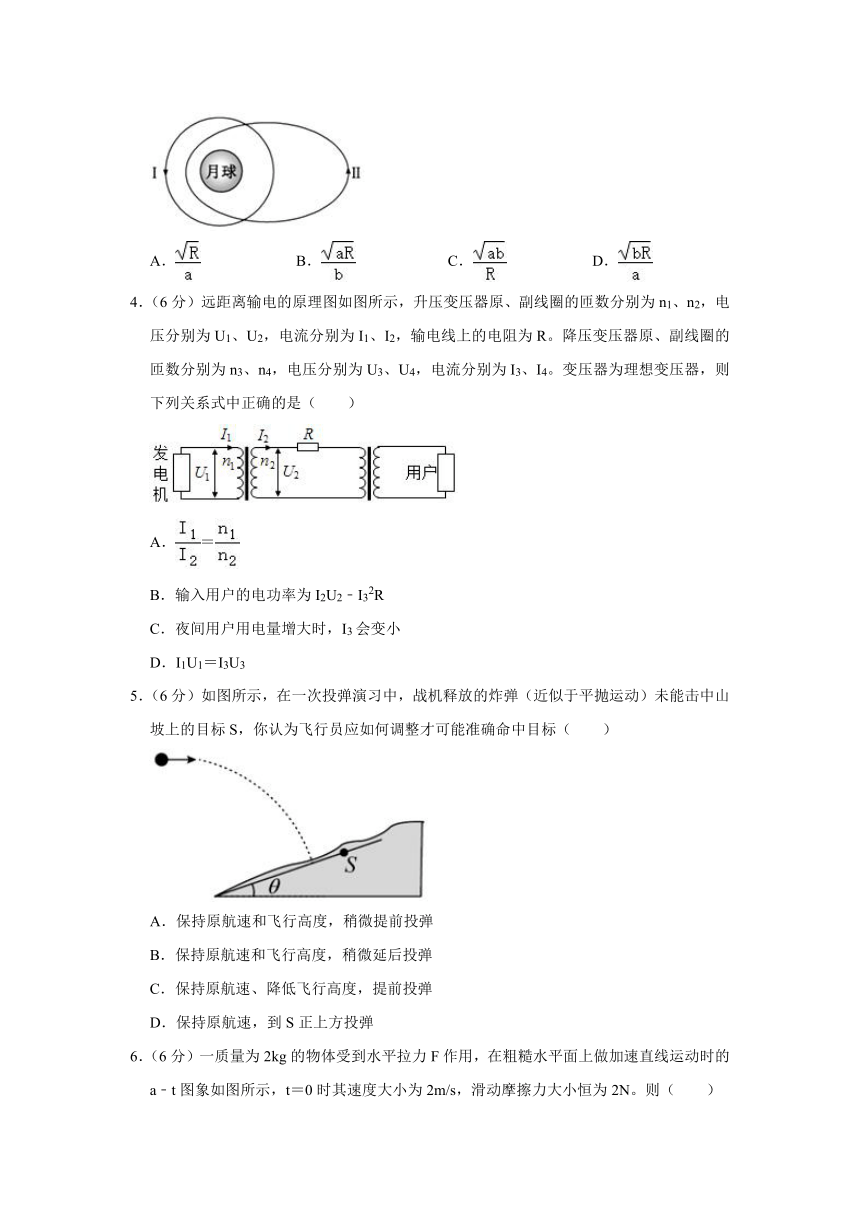
1.(6分)如图所示,图甲为氢原子的能级图,大量处于n=4激发态的氢原子跃迁时,发出频率不同的大量光子。其中频率最高的光子照射到图乙电路中光电管阴极K上时,电路中电流随电压变化的图象如图丙。下列说法正确的是( )
A.阴极K的逸出功为6eV
B.氢原子跃迁时共发出4种频率的光
C.光电子最大初动能与入射光的频率成正比
D.氢原子跃迁放出的光子中有3种频率的光子可以使阴极K发生光电效应现象
2.(6分)如图所示,平行板电容器带有等量异种电荷(上极板带正电),与静电计相连,静电计金属外壳和电容器下极板都接地,在两极板间有一固定在P点的正点电荷,以E表示两板间的电场强度,U表示两板之间的电势差,Ep表示点电荷在P点的电势能,θ表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则( )
A.E不变,Ep不变 B.U不变,E减小
C.θ增大,E不变 D.θ不变,Ep增大
3.(6分)如图所示,轨道Ⅰ为圆形轨道,其半径为R;轨道Ⅱ为椭圆轨道,半长轴为a,半短轴为b。如果把探测器与月球球心连线扫过的面积与所用时间的比值定义为面积速率,则探测器绕月球运动过程中在轨道Ⅰ和轨道Ⅱ上的面积速率之比为(已知椭圆的面积S=πab)( )
A. B. C. D.
4.(6分)远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R。降压变压器原、副线圈的匝数分别为n3、n4,电压分别为U3、U4,电流分别为I3、I4。变压器为理想变压器,则下列关系式中正确的是( )
A.=
B.输入用户的电功率为I2U2﹣I32R
C.夜间用户用电量增大时,I3会变小
D.I1U1=I3U3
5.(6分)如图所示,在一次投弹演习中,战机释放的炸弹(近似于平抛运动)未能击中山坡上的目标S,你认为飞行员应如何调整才可能准确命中目标( )
A.保持原航速和飞行高度,稍微提前投弹
B.保持原航速和飞行高度,稍微延后投弹
C.保持原航速、降低飞行高度,提前投弹
D.保持原航速,到S正上方投弹
6.(6分)一质量为2kg的物体受到水平拉力F作用,在粗糙水平面上做加速直线运动时的a﹣t图象如图所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N。则( )
A.在t=6s时刻,物体的速度为18m/s
B.在0~6s时间内,合力对物体做的功为400J
C.在0~6s时间内,拉力对物体的冲量为48N s
D.在t=6s时刻,拉力F的功率为200W
7.(6分)如图,质量为m、长为L的直导线用两根轻质绝缘细线悬挂于OO1,并处于匀强磁场中、当导线中通以沿y正方向的电流I,且导线保持静止时,细线与竖直方向的夹角为θ。则磁感应强度的方向和大小可能是( )
A.x负向,tanθ B.y正向,tanθ
C.z负向, D.沿悬线向下,sinθ
8.(6分)如图所示,ab、ac、ad、ae是竖直面内的四根固定的细杆,四根细杆与竖直方向的夹角分别为0、30°、45°、60°,a、b、c、d、e点位于同一圆周上,a点为圆周的最高点。每根杆上都套着一个相同的小滑环(圆中未画出),小滑环与细杆之间的动摩擦因数为μ.当四个小滑环从a点由静止释放分别沿细杆滑到另一端的过程中,以下说法正确的是( )
A.所用时间的关系为:tb=tc=td=te
B.末速度的关系为:vb>vc>vd>ve
C.损失的机械能关系为:△Eb<△Ec<△Ed<△Ee
D.产生的热量关系为:Qb<Qc=Qe<Qd
二.实验题(共4小题,满分47分)
9.(6分)某同学用如图所示的实验装置来探究求合力的方法。弹簧测力计A挂于固定点P,下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线方向。
(1)本实验用的弹簧测力计示数的单位为N,图中A的示数为 N。
(2)关于本实验的要求,下列说法正确的是 。
A.实验时不需要测量重物M所受的重力
B.改变拉力,进行多次实验,每次都要使O点静止在同一位置
C.实验时需要记录弹簧测力计的示数和细线方向
D.弹簧测力计在使用前应该校零
(3)某次实验中,该同学发现弹簧测力计A的指针稍稍超出量程,请提出两个解决办法 。
10.(9分)某同学要测量一均匀新材料制成的圆柱体的电阻率ρ,步骤如下:
(1)用游标卡尺测量其长度如图甲所示,由图可知其长度为L= mm。
(2)用螺旋测微器测量其直径如图乙所示,由图可知其直径D= mm。
(3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘示数如图丙所示,则该电阻的阻值约为 Ω。
(4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下:
待测圆柱体电阻R;
电流表A(量程0~30mA,内阻约30Ω);
电压表V(量程0~3V,内阻约10kΩ);
直流电源E(电动势4V,内阻不计);
滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A);
开关S,导线若干。
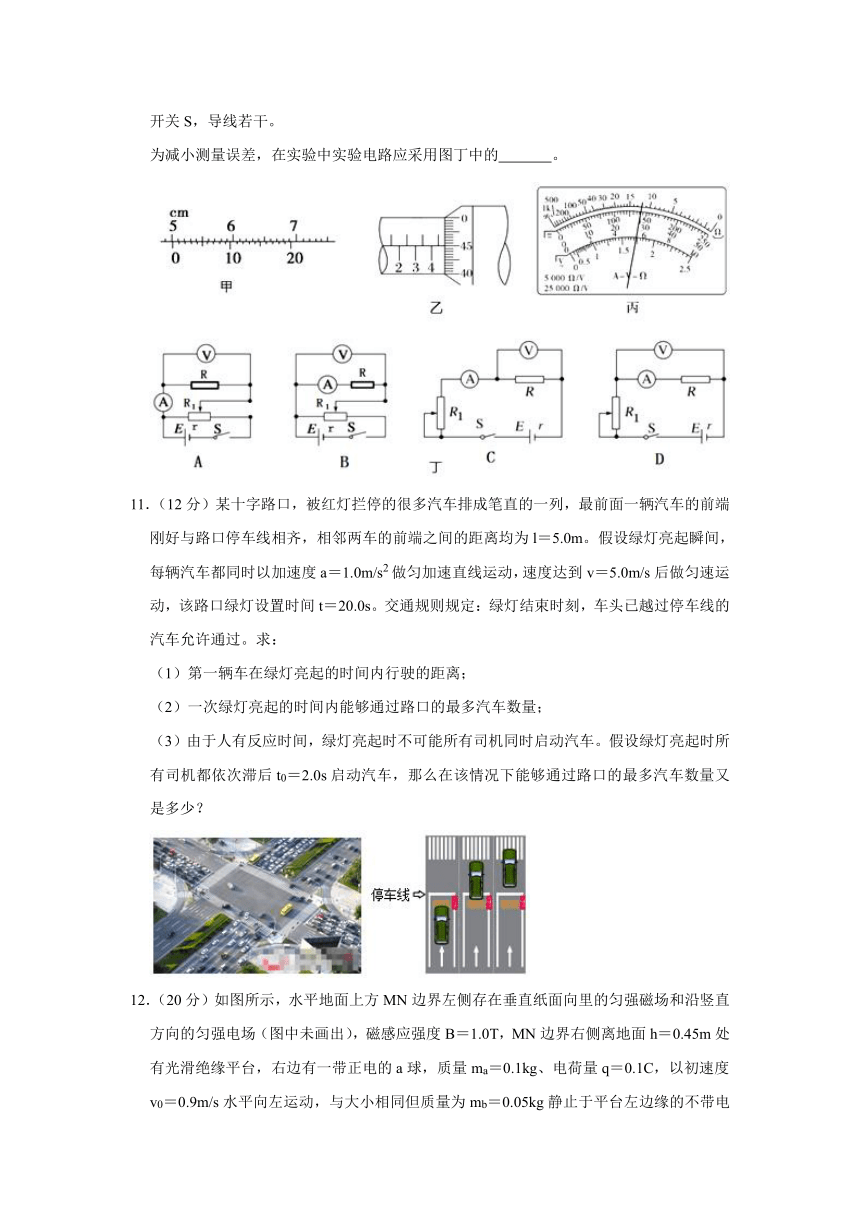
为减小测量误差,在实验中实验电路应采用图丁中的 。
11.(12分)某十字路口,被红灯拦停的很多汽车排成笔直的一列,最前面一辆汽车的前端刚好与路口停车线相齐,相邻两车的前端之间的距离均为l=5.0m。假设绿灯亮起瞬间,每辆汽车都同时以加速度a=1.0m/s2做匀加速直线运动,速度达到v=5.0m/s后做匀速运动,该路口绿灯设置时间t=20.0s。交通规则规定:绿灯结束时刻,车头已越过停车线的汽车允许通过。求:
(1)第一辆车在绿灯亮起的时间内行驶的距离;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量;
(3)由于人有反应时间,绿灯亮起时不可能所有司机同时启动汽车。假设绿灯亮起时所有司机都依次滞后t0=2.0s启动汽车,那么在该情况下能够通过路口的最多汽车数量又是多少?
12.(20分)如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场(图中未画出),磁感应强度B=1.0T,MN边界右侧离地面h=0.45m处有光滑绝缘平台,右边有一带正电的a球,质量ma=0.1kg、电荷量q=0.1C,以初速度v0=0.9m/s水平向左运动,与大小相同但质量为mb=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点且落地后均不反弹,g取10m/s2(结果均保留两位有效数字)。求:
(1)电场强度的大小和方向;
(2)碰后瞬间两球的速度大小;
(3)碰后两球分别在电磁场中运动的时间。
三.多选题(共2小题,满分15分)
13.(5分)下列说法正确的是( )
A.一切晶体的光学和力学性质都是各向异性的
B.在完全失重的宇宙飞船中,水的表面存在表面张力
C.当分子间的距离变小时,分子间作用力的合力可能减小,也可能增大
D.一切与热现象有关的宏观自然过程都是可逆的
E.脱脂棉脱脂的目的在于使它从不能被水浸润变为可以被水浸润,以便吸取药液
14.(10分)如图所示,体积为V0的导热容器被一光滑导热活塞C(厚度忽略不计)分成A、B两个气室,各封闭一定质量的气体,平衡时B室的体积是A室体积的三倍,A室容器上连接有一管内气体体积不计的足够长U形管,两侧水银柱高度差为76cm,B室容器可通过一阀门K与大气相通。已知外界大气压p0=76cmHg,环境温度T0=300K。
(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是多少?
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,求此时A室内气体压强。
四.填空题(共2小题)
15.图甲为一列沿x轴方向传播的简谐横波在t=1时的波形图,P、Q是平衡位置在xp=1m、xQ=2.5m处的两个质点,图乙为质点为P的振动图象。质点P的振动方程为y= cm(用余弦函数表示);从t=1s时开始,质点Q第一次回到平衡位置所需的时间为 s。
16.如图所示为某种透明材料制成的棱镜的横截面图,ABOD为矩形,CD是半径为R的四分之一圆弧,圆心为O;一束平行光线从AB上射入,入射角为θ,其中从M点入射的光线进入棱镜后恰好在BC上的O点发生全反射,然后由CD射出。已知OB段的长度为L,真空中的光速为c。求:
(i)该透明材料的折射率n;
(ii)若透明材料的折射率n=,L=R,不考虑光在CD上的反射,求能从CD上射出的光线对应的圆心角α。
2021-2022学年广西河池市高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)如图所示,图甲为氢原子的能级图,大量处于n=4激发态的氢原子跃迁时,发出频率不同的大量光子。其中频率最高的光子照射到图乙电路中光电管阴极K上时,电路中电流随电压变化的图象如图丙。下列说法正确的是( )
A.阴极K的逸出功为6eV
B.氢原子跃迁时共发出4种频率的光
C.光电子最大初动能与入射光的频率成正比
D.氢原子跃迁放出的光子中有3种频率的光子可以使阴极K发生光电效应现象
【解答】解:A、大量处于n=4激发态的氢原子跃迁时,发出频率最高的光子是对应着从n=4到n=1的跃迁,频率最高光子的能量为hvm=E4﹣E1=﹣0.85eV﹣(﹣13.6eV)=12.75eV,由图可知辐射光电子的最大初动能为6eV,根Ekm=hv﹣W可知,金属的逸出功W=12.75eV﹣6eV=6.75eV,故A错误;
BD、从n=4到低能级的跃迁中能辐射出6种不同频率的光子,其中光子能量大于6.75eV的跃迁有:
n=2到n=1的跃迁,辐射光子的能量为△E1=﹣3.4eV﹣(﹣13.6eV)=10.2eV;
n=3到n=1的跃迁,辐射光子的能量为△E2=﹣1.51eV﹣(﹣13.6eV)=12.09eV;
n=4到n=1的跃迁,辐射光子的能量为△E3=﹣0.85eV﹣(﹣13.6eV)=12.75eV;
其余跃迁光子能量小于6.75eV:
n=4到n=2的跃迁,辐射光子的能量△E4=﹣0.85eV﹣(﹣3.4eV)=2.55eV;
所以各种频率的光分别照射到电路阴极K上,共有3种频率的光能产生光电流,故B错误,D正确;
C、根据爱因斯坦光电效应方程可知,Ekm=hv﹣W,光电子最大初动能随入射光的频率的增大而增大,但不成正比,故C错误;
故选:D。
2.(6分)如图所示,平行板电容器带有等量异种电荷(上极板带正电),与静电计相连,静电计金属外壳和电容器下极板都接地,在两极板间有一固定在P点的正点电荷,以E表示两板间的电场强度,U表示两板之间的电势差,Ep表示点电荷在P点的电势能,θ表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则( )
A.E不变,Ep不变 B.U不变,E减小
C.θ增大,E不变 D.θ不变,Ep增大
【解答】解:电容器与电源断开,故电量Q不变;将上极板向下移动一小段距离至图中虚线位置时,两板间的距离减小,根据C= 可知,电容C增大,则根据C=可知,电压U减小,故静电计指针偏角θ减小;
再根据设P与下极板距离为L,则P点的电势φP=EL,电势能EP=qEL;因此电荷在P点的电势能EP保持不变;
两板间的电场强度E===;因此电场强度与板间距无关,因此电场强度E不变;
综上所述,故A正确,BCD错误;
故选:A。
3.(6分)如图所示,轨道Ⅰ为圆形轨道,其半径为R;轨道Ⅱ为椭圆轨道,半长轴为a,半短轴为b。如果把探测器与月球球心连线扫过的面积与所用时间的比值定义为面积速率,则探测器绕月球运动过程中在轨道Ⅰ和轨道Ⅱ上的面积速率之比为(已知椭圆的面积S=πab)( )
A. B. C. D.
【解答】解:由开普勒第三定律得:=
解得:=
根据探测器与月球的连线面积与其所用时间的比值定义为面积速率得:====
故ACD错误,B正确。
故选:B。
4.(6分)远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R。降压变压器原、副线圈的匝数分别为n3、n4,电压分别为U3、U4,电流分别为I3、I4。变压器为理想变压器,则下列关系式中正确的是( )
A.=
B.输入用户的电功率为I2U2﹣I32R
C.夜间用户用电量增大时,I3会变小
D.I1U1=I3U3
【解答】解:A、升压变压器电流之比与匝数成反比,即;故A错误;
B、变压器输入功率等于输出功率,则发电机的输出功率为P1=U2I2,输电线路上损失的功率为:,故用户得到的功率,故B正确;
C、夜间用户用电量增大时,用户电流增大,输电电流增大,降压变压器的副线圈中的电流变大,降压变压器原线圈电流增大,I3会变大,故C错误;
D、由于输电线路中有电能损失,故,故D错误;
故选:B。
5.(6分)如图所示,在一次投弹演习中,战机释放的炸弹(近似于平抛运动)未能击中山坡上的目标S,你认为飞行员应如何调整才可能准确命中目标( )
A.保持原航速和飞行高度,稍微提前投弹
B.保持原航速和飞行高度,稍微延后投弹
C.保持原航速、降低飞行高度,提前投弹
D.保持原航速,到S正上方投弹
【解答】解:AB、保持原航速和飞行高度,则飞行轨迹不变,要想命中目标,则轨迹需要向右平移,即需要稍微延后投弹,故A错误,B正确;
C、保持原航速、降低飞行高度,则相当于飞行轨迹向下平移,要想命中目标,需要轨迹向右平移,即需要延后投弹,故C错误;
D、保持原航速,到S正上方投弹,则落点在S的右边,故D错误。
故选:B。
6.(6分)一质量为2kg的物体受到水平拉力F作用,在粗糙水平面上做加速直线运动时的a﹣t图象如图所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N。则( )
A.在t=6s时刻,物体的速度为18m/s
B.在0~6s时间内,合力对物体做的功为400J
C.在0~6s时间内,拉力对物体的冲量为48N s
D.在t=6s时刻,拉力F的功率为200W
【解答】解:A、有题目可知,本题图象为a﹣t图象,a﹣t图象所围成的面积为这段时间内速度增加量的大小,故0~6s图象所围成的面积为:s=(2+4)×6÷2m/s=18m/s,故0~6s速度的增加量为:△v=18m/s,已知t=0时其速度大小为2m/s,故在t=6s时刻,物体的速度为vt=v0+△v=2m/s+18m/s=20m/s,故A错误;
B、对物体由动能定理可得:,代入数据可得:W=J=396J,故B错误;
C、对物体由动量定理可得:I=mvt﹣mv0,代入数据可得:I=2×20N s﹣2×2N s=36N s,此时的冲量为合外力所做的冲量,即I=Ft﹣ft,代入可得:IF=I+ft=36N s+2×6N s=48N s,故C正确;
D、t=6s时,物体的速度为20m/s,由图可知,t=6s时物体的加速度为4m/s2,对物体由牛顿第二定律可得:F﹣f=ma,代入数据可得:F=2N+2×4N=10N,
由瞬时功率的公式可得:P=Fv,代入数据可得:P=10×20W=200W,故D正确;
故选:CD。
7.(6分)如图,质量为m、长为L的直导线用两根轻质绝缘细线悬挂于OO1,并处于匀强磁场中、当导线中通以沿y正方向的电流I,且导线保持静止时,细线与竖直方向的夹角为θ。则磁感应强度的方向和大小可能是( )
A.x负向,tanθ B.y正向,tanθ
C.z负向, D.沿悬线向下,sinθ
【解答】解:A、当磁感应强度的方向沿x负向时,根据左手定则可知直导线所受安培力F方向沿z正向,
根据平衡条件可得,
tanθ==,
解得磁感应强度的大小为B=tanθ,故A正确;
B、当磁感应强度的方向沿y正向时,直导线所受安培力F大小为零,不可能保持静止,故B错误;
C、当磁感应强度的方向沿z负向时,直导线所受安培力F方向沿x负向,不可能保持静止,故C错误;
D、当磁感应强度的方向沿悬线向下时,根据左手定则可知直导线所受安培力F方向垂直于悬线斜向上,
根据平衡条件可得F=BIL=mgsinθ,
解得磁感应强度的大小为B=sinθ,故D正确。
故选:AD。
8.(6分)如图所示,ab、ac、ad、ae是竖直面内的四根固定的细杆,四根细杆与竖直方向的夹角分别为0、30°、45°、60°,a、b、c、d、e点位于同一圆周上,a点为圆周的最高点。每根杆上都套着一个相同的小滑环(圆中未画出),小滑环与细杆之间的动摩擦因数为μ.当四个小滑环从a点由静止释放分别沿细杆滑到另一端的过程中,以下说法正确的是( )
A.所用时间的关系为:tb=tc=td=te
B.末速度的关系为:vb>vc>vd>ve
C.损失的机械能关系为:△Eb<△Ec<△Ed<△Ee
D.产生的热量关系为:Qb<Qc=Qe<Qd
【解答】解:A、滑环沿直径ab下滑时,做自由落体运动,2R=,下滑时间;若滑环从倾斜的轨道上下滑,假设轨道与竖直方向的夹角为θ,则下滑加速度大小为gcosθ﹣μgsinθ,下滑位移为2Rcosθ,根据x=,解得滑环从顶端由静止开始滑动到底端的时间t'=,故倾角不同,下滑时间各不相同,A错误;
B、滑环下滑的加速度a=gcosθ﹣μgsinθ,θ越大,a越小,故ab>ac>ad>ae,又xb>xc>xd>xe,又根据v2=2ax,可知:vb>vc>vd>ve,B正确;
C、损失的机械能全部用来克服摩擦力做功,f=μmgsinθ,运动路程x=2Rcosθ,克服摩擦力做功的表达式为:Wf=fx=μmgRsin2θ,当θ=45°时,表达式取最大值。故Wfd最大,所以沿ad运动,损失的机械能最多,C错误;
D、损失的机械能全部转化为内能,即Q=μmgRsin2θ,因sin(2×30°)=sin(2×60°),故Qc=Qe,又因sin(2×45°)=1最大,故Qd最大。沿ab自由落体无内能产生,故Qb=0,故产生热量的正确排序是:Qb<Qc=Qe<Qd,故D正确。
故选:BD。
二.实验题(共4小题,满分47分)
9.(6分)某同学用如图所示的实验装置来探究求合力的方法。弹簧测力计A挂于固定点P,下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线方向。
(1)本实验用的弹簧测力计示数的单位为N,图中A的示数为 2.20 N。
(2)关于本实验的要求,下列说法正确的是 CD 。
A.实验时不需要测量重物M所受的重力
B.改变拉力,进行多次实验,每次都要使O点静止在同一位置
C.实验时需要记录弹簧测力计的示数和细线方向
D.弹簧测力计在使用前应该校零
(3)某次实验中,该同学发现弹簧测力计A的指针稍稍超出量程,请提出两个解决办法 a.减小重物M的质量;b.将A逆时针适当旋转一定角度(或将B顺时针适当旋转一定角度) 。
【解答】解:(1)测力计的最小刻度为0.1N,再估读一位到最小刻度的下一位,读数为:2.20N。
(2)A、结点O受三个力处于平衡状态,任何两个力的合力与第三个力等大反向;实验采用的是作图法求两力的合力,故需测量重物M所受的重力,故A错误;
B、结合实验原理知,改变拉力,进行多次实验时,不必每次都要使O点静止在同一位置,故B错误;
C、实验时需要记录弹簧测力计的示数和细线方向,以便作出力的图示,故C正确;
D、为了减小误差,弹簧测力计应在使用前校零是必要的操作,故D正确;
故选:CD。
(3)当弹簧测力计A超出其量程,则说明弹簧测力计B与重物这两根细线的力的合力已偏大。又由于挂重物的细线力的方向已确定,所以要么减小重物M的质量,要么将A逆时针适当旋转一定角度或将B顺时针适当旋转一定角度。
故答案为:(1)2.20;
(2)CD;
(3)a.减小重物M的质量;b.将A逆时针适当旋转一定角度(或将B顺时针适当旋转一定角度).
10.(9分)某同学要测量一均匀新材料制成的圆柱体的电阻率ρ,步骤如下:
(1)用游标卡尺测量其长度如图甲所示,由图可知其长度为L= 50.25 mm。
(2)用螺旋测微器测量其直径如图乙所示,由图可知其直径D= 4.950 mm。
(3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘示数如图丙所示,则该电阻的阻值约为 120 Ω。
(4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下:
待测圆柱体电阻R;
电流表A(量程0~30mA,内阻约30Ω);
电压表V(量程0~3V,内阻约10kΩ);
直流电源E(电动势4V,内阻不计);
滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A);
开关S,导线若干。
为减小测量误差,在实验中实验电路应采用图丁中的 A 。
【解答】解:(1)由图示游标卡尺可知,游标尺是20分度的,游标尺的精度是0.05mm,由图示游标卡尺可知,其示数为:50mm+0.05×5m=50.25mm。
(2)由图示螺旋测微器可知,其示数为:4.5mm+45.0×0.01mm=4.950mm。
(3)多用电表的电阻“×10”挡测电阻,由图丙所示表盘可知,电阻阻值为:12×10Ω=120Ω。
(4)由于电压表内阻远大于待测电阻阻值,电流表应采用外接法;待测电阻阻值远大于滑动变阻器最大阻值,为测多组实验数据,滑动变阻器应采用分压接法,因此应选择图A所示电路图。
故答案为:(1)50.25;(2)4.950;(3)120;(4)A。
11.(12分)某十字路口,被红灯拦停的很多汽车排成笔直的一列,最前面一辆汽车的前端刚好与路口停车线相齐,相邻两车的前端之间的距离均为l=5.0m。假设绿灯亮起瞬间,每辆汽车都同时以加速度a=1.0m/s2做匀加速直线运动,速度达到v=5.0m/s后做匀速运动,该路口绿灯设置时间t=20.0s。交通规则规定:绿灯结束时刻,车头已越过停车线的汽车允许通过。求:
(1)第一辆车在绿灯亮起的时间内行驶的距离;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量;
(3)由于人有反应时间,绿灯亮起时不可能所有司机同时启动汽车。假设绿灯亮起时所有司机都依次滞后t0=2.0s启动汽车,那么在该情况下能够通过路口的最多汽车数量又是多少?
【解答】解:(1)设汽车匀加速的时间为t1,根据速度时间公式
v=at1,解得t1=5s,
根据位移公式,解得x1=12.5m
第一辆车在匀速运动内的位移为x2
x2=v(t﹣t1),解得x2=75m
在20s内的位移:x=x1+x2=12.5m+75m=87.5m
(2)通过路口的车辆数
代入数据解得n=17.5
故通过路口的车辆数为18辆.
(3)设能通过k辆汽车,则有
第k辆汽车能通过路口要满足:xk≥(k﹣1)l
代入数据得k≤6.2,所以能通过6辆汽车
答:(1)第一辆车在绿灯亮起的时间内行驶的距离为87.5m;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量为18辆;
(3)在该情况下能够通过路口的最多汽车数量为6辆。
12.(20分)如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场(图中未画出),磁感应强度B=1.0T,MN边界右侧离地面h=0.45m处有光滑绝缘平台,右边有一带正电的a球,质量ma=0.1kg、电荷量q=0.1C,以初速度v0=0.9m/s水平向左运动,与大小相同但质量为mb=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点且落地后均不反弹,g取10m/s2(结果均保留两位有效数字)。求:
(1)电场强度的大小和方向;
(2)碰后瞬间两球的速度大小;
(3)碰后两球分别在电磁场中运动的时间。
【解答】解:
(1)a球碰后做匀速圆周运动,满足mag=qE,可得E=10N/C。
重力竖直向下,静电力竖直向上,而a球带正电,故电场强度方向竖直向上。
(2)规定水平向左为正方向,a球与b球发生弹性正碰,由动量守恒定律得mava=mav0+mbvb﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
由能量守恒定律得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
解得v0=0.3m/s,vb=1.2m/s。﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③
(3)对a球,洛伦兹力提供向心力﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣④
可得r==0.30m﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑤
设a球落地点与球心的连线和地面夹角为θ,由几何关系有h=r+rsinθ,则θ=
故a球在电磁场中运动的时间,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑥
解得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑦
b球不带电,碰撞后做平抛运动,竖直方向有﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑧
解得tb=0.30s﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑨
答:
(1)电场强度为10N/C,方向竖直向上。
(2)碰后瞬间a球的速度0.3m/s,b球的速度为1.2m/s。
(3)碰后a球在磁场中运动时间为,b球在磁场中运动时间为0.30s。
三.多选题(共2小题,满分15分)
13.(5分)下列说法正确的是( )
A.一切晶体的光学和力学性质都是各向异性的
B.在完全失重的宇宙飞船中,水的表面存在表面张力
C.当分子间的距离变小时,分子间作用力的合力可能减小,也可能增大
D.一切与热现象有关的宏观自然过程都是可逆的
E.脱脂棉脱脂的目的在于使它从不能被水浸润变为可以被水浸润,以便吸取药液
【解答】解:A、一切单晶体的物理性质具有各向异性,但多晶体具有各向同性,故A错误;
B、由于液体的蒸发,液体表面分子较为稀疏,故分子间距大于液体内部,表现为引力,分子力与重力无关,故在完全失重的宇宙飞船中,水的表面依然存在表面张力,故B正确;
C、当分子间距离r<r0时,分子间表现为斥力,若分子间距离减小,斥力增大。当r>r0时,分子间表现为引力,分子间距离减小时,分子力可能减小,故C正确;
D、一切与热现象有关的宏观自然过程都具有方向性,是不可逆的,故D错误;
E、脱脂棉能够吸取药液,在于脱脂后把它从不能被水浸润变成了可以被水浸润,故E正确。
故选:BCE。
14.(10分)如图所示,体积为V0的导热容器被一光滑导热活塞C(厚度忽略不计)分成A、B两个气室,各封闭一定质量的气体,平衡时B室的体积是A室体积的三倍,A室容器上连接有一管内气体体积不计的足够长U形管,两侧水银柱高度差为76cm,B室容器可通过一阀门K与大气相通。已知外界大气压p0=76cmHg,环境温度T0=300K。
(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是多少?
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,求此时A室内气体压强。
【解答】解:(ⅰ)开始时,A室内的气体压强为:pA0=p0+ρgh=2p0,A室内的气体体积为:VA0=
打开阀门,A室气体等温变化,稳定后压强为:pA1=p0,体积为VA1
对A室气体,由玻意耳定律得:pA0VA0=pA1VA1
解得:VA1=
B室气体等温变化,稳定后压强为:pB0=pA0,pB1=pA1,VB0=V0﹣VA0=
对B室气体,由玻意耳定律得:pB0VB0=pB1VB1
解得:VB1=
则稳定后B室内剩余气体的质量和B室原有气体质量之比为:===
(ⅱ)假设打开阀门后,气体从T0=300K升到T时,活塞C恰好到达容器最右端,即气体体积变为V0,压强pA仍为p0,即等压变化过程,
则根据盖一吕萨克定律,有=
解得:T1=600K
因为T2=750K>600K,所以温度从T1=600K升高到T2=750K,是等容变化过程,
根据查理定律,有=
代入数据解得此时A室内气体压强为:pA2=95cmHg
答:(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是;
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,此时A室内气体压强为95cmHg。
四.填空题(共2小题)
15.图甲为一列沿x轴方向传播的简谐横波在t=1时的波形图,P、Q是平衡位置在xp=1m、xQ=2.5m处的两个质点,图乙为质点为P的振动图象。质点P的振动方程为y= 4cos cm(用余弦函数表示);从t=1s时开始,质点Q第一次回到平衡位置所需的时间为 1.5 s。
【解答】解:根据图乙可得P的振动为余弦图象,则y=Acosωt=4cos=4cos cm;
t=1s时P向下振动,根据“同侧法”可知该波向右传播,波速v=m/s=1m/s
质点Q第一次回到平衡位置所需的时间为t==s=1.5s。
故答案为:4cos;1.5。
16.如图所示为某种透明材料制成的棱镜的横截面图,ABOD为矩形,CD是半径为R的四分之一圆弧,圆心为O;一束平行光线从AB上射入,入射角为θ,其中从M点入射的光线进入棱镜后恰好在BC上的O点发生全反射,然后由CD射出。已知OB段的长度为L,真空中的光速为c。求:
(i)该透明材料的折射率n;
(ii)若透明材料的折射率n=,L=R,不考虑光在CD上的反射,求能从CD上射出的光线对应的圆心角α。
【解答】解:(1)设光线在AB面的折射角为r,光路如图所示。
根据折射定律得:n=
设棱镜的全反射临界角为θC,由题意知,光线在BC面上的O点恰好发生全反射,入射角等于临界角,则
sinθC=
由几何知识可知:r+θC=90°。
联立以上各式解得:n=;
(ii)若透明材料的折射率n=,由sinθC=解得θC=60°
由r+θC=90°,得r=30°
设刚好在O点发生全反射的光线从CD上的P点射出,由A和B处入射的边界光线分别能到达CD圆弧上的C′点和D′点,在AB上发生折射后直接到达CD上的光线,在C′处与法线间的夹角最大。
则在三角形OEC′中,由正弦定理得
=
由几何关系知∠OEC′=60°,OE<R,则β<60°
故由AB上发生折射后直接射到CD圆弧上的光线不会在CD上发生全反射。
经分析,从AB折射后到达BC经过全反射到达CD圆弧上CP间的光线,在C点处与法线间的夹角最大,且为30°,故不会在CD上发生全反射,CP间有光线从CD上射出。
从AB折射到达BC经过全反射后到达CD圆弧上PD′间的光线在D′射出时与光线间的夹角最大,设到达D′点的光线与OD′间的夹角为θ′,如图2所示,则在三角形OBD′中,由正弦定理得
=
解得sinθ′==
故θ′<60°
光线也不会在CD上发生全反射,故有光线从CD上射出的圆弧范围为CD′,由几何知识得OD′与法线OC间的夹角α=30°+θ′,其中θ′=arcsin。
答:(i)该透明材料的折射率n是;
(ii)能从CD上射出的光线对应的圆心角α是30°+arcsin。
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)如图所示,图甲为氢原子的能级图,大量处于n=4激发态的氢原子跃迁时,发出频率不同的大量光子。其中频率最高的光子照射到图乙电路中光电管阴极K上时,电路中电流随电压变化的图象如图丙。下列说法正确的是( )
A.阴极K的逸出功为6eV
B.氢原子跃迁时共发出4种频率的光
C.光电子最大初动能与入射光的频率成正比
D.氢原子跃迁放出的光子中有3种频率的光子可以使阴极K发生光电效应现象
2.(6分)如图所示,平行板电容器带有等量异种电荷(上极板带正电),与静电计相连,静电计金属外壳和电容器下极板都接地,在两极板间有一固定在P点的正点电荷,以E表示两板间的电场强度,U表示两板之间的电势差,Ep表示点电荷在P点的电势能,θ表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则( )
A.E不变,Ep不变 B.U不变,E减小
C.θ增大,E不变 D.θ不变,Ep增大
3.(6分)如图所示,轨道Ⅰ为圆形轨道,其半径为R;轨道Ⅱ为椭圆轨道,半长轴为a,半短轴为b。如果把探测器与月球球心连线扫过的面积与所用时间的比值定义为面积速率,则探测器绕月球运动过程中在轨道Ⅰ和轨道Ⅱ上的面积速率之比为(已知椭圆的面积S=πab)( )
A. B. C. D.
4.(6分)远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R。降压变压器原、副线圈的匝数分别为n3、n4,电压分别为U3、U4,电流分别为I3、I4。变压器为理想变压器,则下列关系式中正确的是( )
A.=
B.输入用户的电功率为I2U2﹣I32R
C.夜间用户用电量增大时,I3会变小
D.I1U1=I3U3
5.(6分)如图所示,在一次投弹演习中,战机释放的炸弹(近似于平抛运动)未能击中山坡上的目标S,你认为飞行员应如何调整才可能准确命中目标( )
A.保持原航速和飞行高度,稍微提前投弹
B.保持原航速和飞行高度,稍微延后投弹
C.保持原航速、降低飞行高度,提前投弹
D.保持原航速,到S正上方投弹
6.(6分)一质量为2kg的物体受到水平拉力F作用,在粗糙水平面上做加速直线运动时的a﹣t图象如图所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N。则( )
A.在t=6s时刻,物体的速度为18m/s
B.在0~6s时间内,合力对物体做的功为400J
C.在0~6s时间内,拉力对物体的冲量为48N s
D.在t=6s时刻,拉力F的功率为200W
7.(6分)如图,质量为m、长为L的直导线用两根轻质绝缘细线悬挂于OO1,并处于匀强磁场中、当导线中通以沿y正方向的电流I,且导线保持静止时,细线与竖直方向的夹角为θ。则磁感应强度的方向和大小可能是( )
A.x负向,tanθ B.y正向,tanθ
C.z负向, D.沿悬线向下,sinθ
8.(6分)如图所示,ab、ac、ad、ae是竖直面内的四根固定的细杆,四根细杆与竖直方向的夹角分别为0、30°、45°、60°,a、b、c、d、e点位于同一圆周上,a点为圆周的最高点。每根杆上都套着一个相同的小滑环(圆中未画出),小滑环与细杆之间的动摩擦因数为μ.当四个小滑环从a点由静止释放分别沿细杆滑到另一端的过程中,以下说法正确的是( )
A.所用时间的关系为:tb=tc=td=te
B.末速度的关系为:vb>vc>vd>ve
C.损失的机械能关系为:△Eb<△Ec<△Ed<△Ee
D.产生的热量关系为:Qb<Qc=Qe<Qd
二.实验题(共4小题,满分47分)
9.(6分)某同学用如图所示的实验装置来探究求合力的方法。弹簧测力计A挂于固定点P,下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线方向。
(1)本实验用的弹簧测力计示数的单位为N,图中A的示数为 N。
(2)关于本实验的要求,下列说法正确的是 。
A.实验时不需要测量重物M所受的重力
B.改变拉力,进行多次实验,每次都要使O点静止在同一位置
C.实验时需要记录弹簧测力计的示数和细线方向
D.弹簧测力计在使用前应该校零
(3)某次实验中,该同学发现弹簧测力计A的指针稍稍超出量程,请提出两个解决办法 。
10.(9分)某同学要测量一均匀新材料制成的圆柱体的电阻率ρ,步骤如下:
(1)用游标卡尺测量其长度如图甲所示,由图可知其长度为L= mm。
(2)用螺旋测微器测量其直径如图乙所示,由图可知其直径D= mm。
(3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘示数如图丙所示,则该电阻的阻值约为 Ω。
(4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下:
待测圆柱体电阻R;
电流表A(量程0~30mA,内阻约30Ω);
电压表V(量程0~3V,内阻约10kΩ);
直流电源E(电动势4V,内阻不计);
滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A);
开关S,导线若干。
为减小测量误差,在实验中实验电路应采用图丁中的 。
11.(12分)某十字路口,被红灯拦停的很多汽车排成笔直的一列,最前面一辆汽车的前端刚好与路口停车线相齐,相邻两车的前端之间的距离均为l=5.0m。假设绿灯亮起瞬间,每辆汽车都同时以加速度a=1.0m/s2做匀加速直线运动,速度达到v=5.0m/s后做匀速运动,该路口绿灯设置时间t=20.0s。交通规则规定:绿灯结束时刻,车头已越过停车线的汽车允许通过。求:
(1)第一辆车在绿灯亮起的时间内行驶的距离;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量;
(3)由于人有反应时间,绿灯亮起时不可能所有司机同时启动汽车。假设绿灯亮起时所有司机都依次滞后t0=2.0s启动汽车,那么在该情况下能够通过路口的最多汽车数量又是多少?
12.(20分)如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场(图中未画出),磁感应强度B=1.0T,MN边界右侧离地面h=0.45m处有光滑绝缘平台,右边有一带正电的a球,质量ma=0.1kg、电荷量q=0.1C,以初速度v0=0.9m/s水平向左运动,与大小相同但质量为mb=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点且落地后均不反弹,g取10m/s2(结果均保留两位有效数字)。求:
(1)电场强度的大小和方向;
(2)碰后瞬间两球的速度大小;
(3)碰后两球分别在电磁场中运动的时间。
三.多选题(共2小题,满分15分)
13.(5分)下列说法正确的是( )
A.一切晶体的光学和力学性质都是各向异性的
B.在完全失重的宇宙飞船中,水的表面存在表面张力
C.当分子间的距离变小时,分子间作用力的合力可能减小,也可能增大
D.一切与热现象有关的宏观自然过程都是可逆的
E.脱脂棉脱脂的目的在于使它从不能被水浸润变为可以被水浸润,以便吸取药液
14.(10分)如图所示,体积为V0的导热容器被一光滑导热活塞C(厚度忽略不计)分成A、B两个气室,各封闭一定质量的气体,平衡时B室的体积是A室体积的三倍,A室容器上连接有一管内气体体积不计的足够长U形管,两侧水银柱高度差为76cm,B室容器可通过一阀门K与大气相通。已知外界大气压p0=76cmHg,环境温度T0=300K。
(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是多少?
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,求此时A室内气体压强。
四.填空题(共2小题)
15.图甲为一列沿x轴方向传播的简谐横波在t=1时的波形图,P、Q是平衡位置在xp=1m、xQ=2.5m处的两个质点,图乙为质点为P的振动图象。质点P的振动方程为y= cm(用余弦函数表示);从t=1s时开始,质点Q第一次回到平衡位置所需的时间为 s。
16.如图所示为某种透明材料制成的棱镜的横截面图,ABOD为矩形,CD是半径为R的四分之一圆弧,圆心为O;一束平行光线从AB上射入,入射角为θ,其中从M点入射的光线进入棱镜后恰好在BC上的O点发生全反射,然后由CD射出。已知OB段的长度为L,真空中的光速为c。求:
(i)该透明材料的折射率n;
(ii)若透明材料的折射率n=,L=R,不考虑光在CD上的反射,求能从CD上射出的光线对应的圆心角α。
2021-2022学年广西河池市高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)如图所示,图甲为氢原子的能级图,大量处于n=4激发态的氢原子跃迁时,发出频率不同的大量光子。其中频率最高的光子照射到图乙电路中光电管阴极K上时,电路中电流随电压变化的图象如图丙。下列说法正确的是( )
A.阴极K的逸出功为6eV
B.氢原子跃迁时共发出4种频率的光
C.光电子最大初动能与入射光的频率成正比
D.氢原子跃迁放出的光子中有3种频率的光子可以使阴极K发生光电效应现象
【解答】解:A、大量处于n=4激发态的氢原子跃迁时,发出频率最高的光子是对应着从n=4到n=1的跃迁,频率最高光子的能量为hvm=E4﹣E1=﹣0.85eV﹣(﹣13.6eV)=12.75eV,由图可知辐射光电子的最大初动能为6eV,根Ekm=hv﹣W可知,金属的逸出功W=12.75eV﹣6eV=6.75eV,故A错误;
BD、从n=4到低能级的跃迁中能辐射出6种不同频率的光子,其中光子能量大于6.75eV的跃迁有:
n=2到n=1的跃迁,辐射光子的能量为△E1=﹣3.4eV﹣(﹣13.6eV)=10.2eV;
n=3到n=1的跃迁,辐射光子的能量为△E2=﹣1.51eV﹣(﹣13.6eV)=12.09eV;
n=4到n=1的跃迁,辐射光子的能量为△E3=﹣0.85eV﹣(﹣13.6eV)=12.75eV;
其余跃迁光子能量小于6.75eV:
n=4到n=2的跃迁,辐射光子的能量△E4=﹣0.85eV﹣(﹣3.4eV)=2.55eV;
所以各种频率的光分别照射到电路阴极K上,共有3种频率的光能产生光电流,故B错误,D正确;
C、根据爱因斯坦光电效应方程可知,Ekm=hv﹣W,光电子最大初动能随入射光的频率的增大而增大,但不成正比,故C错误;
故选:D。
2.(6分)如图所示,平行板电容器带有等量异种电荷(上极板带正电),与静电计相连,静电计金属外壳和电容器下极板都接地,在两极板间有一固定在P点的正点电荷,以E表示两板间的电场强度,U表示两板之间的电势差,Ep表示点电荷在P点的电势能,θ表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则( )
A.E不变,Ep不变 B.U不变,E减小
C.θ增大,E不变 D.θ不变,Ep增大
【解答】解:电容器与电源断开,故电量Q不变;将上极板向下移动一小段距离至图中虚线位置时,两板间的距离减小,根据C= 可知,电容C增大,则根据C=可知,电压U减小,故静电计指针偏角θ减小;
再根据设P与下极板距离为L,则P点的电势φP=EL,电势能EP=qEL;因此电荷在P点的电势能EP保持不变;
两板间的电场强度E===;因此电场强度与板间距无关,因此电场强度E不变;
综上所述,故A正确,BCD错误;
故选:A。
3.(6分)如图所示,轨道Ⅰ为圆形轨道,其半径为R;轨道Ⅱ为椭圆轨道,半长轴为a,半短轴为b。如果把探测器与月球球心连线扫过的面积与所用时间的比值定义为面积速率,则探测器绕月球运动过程中在轨道Ⅰ和轨道Ⅱ上的面积速率之比为(已知椭圆的面积S=πab)( )
A. B. C. D.
【解答】解:由开普勒第三定律得:=
解得:=
根据探测器与月球的连线面积与其所用时间的比值定义为面积速率得:====
故ACD错误,B正确。
故选:B。
4.(6分)远距离输电的原理图如图所示,升压变压器原、副线圈的匝数分别为n1、n2,电压分别为U1、U2,电流分别为I1、I2,输电线上的电阻为R。降压变压器原、副线圈的匝数分别为n3、n4,电压分别为U3、U4,电流分别为I3、I4。变压器为理想变压器,则下列关系式中正确的是( )
A.=
B.输入用户的电功率为I2U2﹣I32R
C.夜间用户用电量增大时,I3会变小
D.I1U1=I3U3
【解答】解:A、升压变压器电流之比与匝数成反比,即;故A错误;
B、变压器输入功率等于输出功率,则发电机的输出功率为P1=U2I2,输电线路上损失的功率为:,故用户得到的功率,故B正确;
C、夜间用户用电量增大时,用户电流增大,输电电流增大,降压变压器的副线圈中的电流变大,降压变压器原线圈电流增大,I3会变大,故C错误;
D、由于输电线路中有电能损失,故,故D错误;
故选:B。
5.(6分)如图所示,在一次投弹演习中,战机释放的炸弹(近似于平抛运动)未能击中山坡上的目标S,你认为飞行员应如何调整才可能准确命中目标( )
A.保持原航速和飞行高度,稍微提前投弹
B.保持原航速和飞行高度,稍微延后投弹
C.保持原航速、降低飞行高度,提前投弹
D.保持原航速,到S正上方投弹
【解答】解:AB、保持原航速和飞行高度,则飞行轨迹不变,要想命中目标,则轨迹需要向右平移,即需要稍微延后投弹,故A错误,B正确;
C、保持原航速、降低飞行高度,则相当于飞行轨迹向下平移,要想命中目标,需要轨迹向右平移,即需要延后投弹,故C错误;
D、保持原航速,到S正上方投弹,则落点在S的右边,故D错误。
故选:B。
6.(6分)一质量为2kg的物体受到水平拉力F作用,在粗糙水平面上做加速直线运动时的a﹣t图象如图所示,t=0时其速度大小为2m/s,滑动摩擦力大小恒为2N。则( )
A.在t=6s时刻,物体的速度为18m/s
B.在0~6s时间内,合力对物体做的功为400J
C.在0~6s时间内,拉力对物体的冲量为48N s
D.在t=6s时刻,拉力F的功率为200W
【解答】解:A、有题目可知,本题图象为a﹣t图象,a﹣t图象所围成的面积为这段时间内速度增加量的大小,故0~6s图象所围成的面积为:s=(2+4)×6÷2m/s=18m/s,故0~6s速度的增加量为:△v=18m/s,已知t=0时其速度大小为2m/s,故在t=6s时刻,物体的速度为vt=v0+△v=2m/s+18m/s=20m/s,故A错误;
B、对物体由动能定理可得:,代入数据可得:W=J=396J,故B错误;
C、对物体由动量定理可得:I=mvt﹣mv0,代入数据可得:I=2×20N s﹣2×2N s=36N s,此时的冲量为合外力所做的冲量,即I=Ft﹣ft,代入可得:IF=I+ft=36N s+2×6N s=48N s,故C正确;
D、t=6s时,物体的速度为20m/s,由图可知,t=6s时物体的加速度为4m/s2,对物体由牛顿第二定律可得:F﹣f=ma,代入数据可得:F=2N+2×4N=10N,
由瞬时功率的公式可得:P=Fv,代入数据可得:P=10×20W=200W,故D正确;
故选:CD。
7.(6分)如图,质量为m、长为L的直导线用两根轻质绝缘细线悬挂于OO1,并处于匀强磁场中、当导线中通以沿y正方向的电流I,且导线保持静止时,细线与竖直方向的夹角为θ。则磁感应强度的方向和大小可能是( )
A.x负向,tanθ B.y正向,tanθ
C.z负向, D.沿悬线向下,sinθ
【解答】解:A、当磁感应强度的方向沿x负向时,根据左手定则可知直导线所受安培力F方向沿z正向,
根据平衡条件可得,
tanθ==,
解得磁感应强度的大小为B=tanθ,故A正确;
B、当磁感应强度的方向沿y正向时,直导线所受安培力F大小为零,不可能保持静止,故B错误;
C、当磁感应强度的方向沿z负向时,直导线所受安培力F方向沿x负向,不可能保持静止,故C错误;
D、当磁感应强度的方向沿悬线向下时,根据左手定则可知直导线所受安培力F方向垂直于悬线斜向上,
根据平衡条件可得F=BIL=mgsinθ,
解得磁感应强度的大小为B=sinθ,故D正确。
故选:AD。
8.(6分)如图所示,ab、ac、ad、ae是竖直面内的四根固定的细杆,四根细杆与竖直方向的夹角分别为0、30°、45°、60°,a、b、c、d、e点位于同一圆周上,a点为圆周的最高点。每根杆上都套着一个相同的小滑环(圆中未画出),小滑环与细杆之间的动摩擦因数为μ.当四个小滑环从a点由静止释放分别沿细杆滑到另一端的过程中,以下说法正确的是( )
A.所用时间的关系为:tb=tc=td=te
B.末速度的关系为:vb>vc>vd>ve
C.损失的机械能关系为:△Eb<△Ec<△Ed<△Ee
D.产生的热量关系为:Qb<Qc=Qe<Qd
【解答】解:A、滑环沿直径ab下滑时,做自由落体运动,2R=,下滑时间;若滑环从倾斜的轨道上下滑,假设轨道与竖直方向的夹角为θ,则下滑加速度大小为gcosθ﹣μgsinθ,下滑位移为2Rcosθ,根据x=,解得滑环从顶端由静止开始滑动到底端的时间t'=,故倾角不同,下滑时间各不相同,A错误;
B、滑环下滑的加速度a=gcosθ﹣μgsinθ,θ越大,a越小,故ab>ac>ad>ae,又xb>xc>xd>xe,又根据v2=2ax,可知:vb>vc>vd>ve,B正确;
C、损失的机械能全部用来克服摩擦力做功,f=μmgsinθ,运动路程x=2Rcosθ,克服摩擦力做功的表达式为:Wf=fx=μmgRsin2θ,当θ=45°时,表达式取最大值。故Wfd最大,所以沿ad运动,损失的机械能最多,C错误;
D、损失的机械能全部转化为内能,即Q=μmgRsin2θ,因sin(2×30°)=sin(2×60°),故Qc=Qe,又因sin(2×45°)=1最大,故Qd最大。沿ab自由落体无内能产生,故Qb=0,故产生热量的正确排序是:Qb<Qc=Qe<Qd,故D正确。
故选:BD。
二.实验题(共4小题,满分47分)
9.(6分)某同学用如图所示的实验装置来探究求合力的方法。弹簧测力计A挂于固定点P,下端用细线挂一重物M。弹簧测力计B的一端用细线系于O点,手持另一端水平向左拉,使结点O静止在某位置,分别读出弹簧测力计A和B的示数,并在贴于竖直木板的白纸上记录O点的位置和拉线方向。
(1)本实验用的弹簧测力计示数的单位为N,图中A的示数为 2.20 N。
(2)关于本实验的要求,下列说法正确的是 CD 。
A.实验时不需要测量重物M所受的重力
B.改变拉力,进行多次实验,每次都要使O点静止在同一位置
C.实验时需要记录弹簧测力计的示数和细线方向
D.弹簧测力计在使用前应该校零
(3)某次实验中,该同学发现弹簧测力计A的指针稍稍超出量程,请提出两个解决办法 a.减小重物M的质量;b.将A逆时针适当旋转一定角度(或将B顺时针适当旋转一定角度) 。
【解答】解:(1)测力计的最小刻度为0.1N,再估读一位到最小刻度的下一位,读数为:2.20N。
(2)A、结点O受三个力处于平衡状态,任何两个力的合力与第三个力等大反向;实验采用的是作图法求两力的合力,故需测量重物M所受的重力,故A错误;
B、结合实验原理知,改变拉力,进行多次实验时,不必每次都要使O点静止在同一位置,故B错误;
C、实验时需要记录弹簧测力计的示数和细线方向,以便作出力的图示,故C正确;
D、为了减小误差,弹簧测力计应在使用前校零是必要的操作,故D正确;
故选:CD。
(3)当弹簧测力计A超出其量程,则说明弹簧测力计B与重物这两根细线的力的合力已偏大。又由于挂重物的细线力的方向已确定,所以要么减小重物M的质量,要么将A逆时针适当旋转一定角度或将B顺时针适当旋转一定角度。
故答案为:(1)2.20;
(2)CD;
(3)a.减小重物M的质量;b.将A逆时针适当旋转一定角度(或将B顺时针适当旋转一定角度).
10.(9分)某同学要测量一均匀新材料制成的圆柱体的电阻率ρ,步骤如下:
(1)用游标卡尺测量其长度如图甲所示,由图可知其长度为L= 50.25 mm。
(2)用螺旋测微器测量其直径如图乙所示,由图可知其直径D= 4.950 mm。
(3)用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘示数如图丙所示,则该电阻的阻值约为 120 Ω。
(4)该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下:
待测圆柱体电阻R;
电流表A(量程0~30mA,内阻约30Ω);
电压表V(量程0~3V,内阻约10kΩ);
直流电源E(电动势4V,内阻不计);
滑动变阻器R1(阻值范围0~15Ω,允许通过的最大电流2.0A);
开关S,导线若干。
为减小测量误差,在实验中实验电路应采用图丁中的 A 。
【解答】解:(1)由图示游标卡尺可知,游标尺是20分度的,游标尺的精度是0.05mm,由图示游标卡尺可知,其示数为:50mm+0.05×5m=50.25mm。
(2)由图示螺旋测微器可知,其示数为:4.5mm+45.0×0.01mm=4.950mm。
(3)多用电表的电阻“×10”挡测电阻,由图丙所示表盘可知,电阻阻值为:12×10Ω=120Ω。
(4)由于电压表内阻远大于待测电阻阻值,电流表应采用外接法;待测电阻阻值远大于滑动变阻器最大阻值,为测多组实验数据,滑动变阻器应采用分压接法,因此应选择图A所示电路图。
故答案为:(1)50.25;(2)4.950;(3)120;(4)A。
11.(12分)某十字路口,被红灯拦停的很多汽车排成笔直的一列,最前面一辆汽车的前端刚好与路口停车线相齐,相邻两车的前端之间的距离均为l=5.0m。假设绿灯亮起瞬间,每辆汽车都同时以加速度a=1.0m/s2做匀加速直线运动,速度达到v=5.0m/s后做匀速运动,该路口绿灯设置时间t=20.0s。交通规则规定:绿灯结束时刻,车头已越过停车线的汽车允许通过。求:
(1)第一辆车在绿灯亮起的时间内行驶的距离;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量;
(3)由于人有反应时间,绿灯亮起时不可能所有司机同时启动汽车。假设绿灯亮起时所有司机都依次滞后t0=2.0s启动汽车,那么在该情况下能够通过路口的最多汽车数量又是多少?
【解答】解:(1)设汽车匀加速的时间为t1,根据速度时间公式
v=at1,解得t1=5s,
根据位移公式,解得x1=12.5m
第一辆车在匀速运动内的位移为x2
x2=v(t﹣t1),解得x2=75m
在20s内的位移:x=x1+x2=12.5m+75m=87.5m
(2)通过路口的车辆数
代入数据解得n=17.5
故通过路口的车辆数为18辆.
(3)设能通过k辆汽车,则有
第k辆汽车能通过路口要满足:xk≥(k﹣1)l
代入数据得k≤6.2,所以能通过6辆汽车
答:(1)第一辆车在绿灯亮起的时间内行驶的距离为87.5m;
(2)一次绿灯亮起的时间内能够通过路口的最多汽车数量为18辆;
(3)在该情况下能够通过路口的最多汽车数量为6辆。
12.(20分)如图所示,水平地面上方MN边界左侧存在垂直纸面向里的匀强磁场和沿竖直方向的匀强电场(图中未画出),磁感应强度B=1.0T,MN边界右侧离地面h=0.45m处有光滑绝缘平台,右边有一带正电的a球,质量ma=0.1kg、电荷量q=0.1C,以初速度v0=0.9m/s水平向左运动,与大小相同但质量为mb=0.05kg静止于平台左边缘的不带电的绝缘球b发生弹性正碰,碰后a球恰好做匀速圆周运动,两球均视为质点且落地后均不反弹,g取10m/s2(结果均保留两位有效数字)。求:
(1)电场强度的大小和方向;
(2)碰后瞬间两球的速度大小;
(3)碰后两球分别在电磁场中运动的时间。
【解答】解:
(1)a球碰后做匀速圆周运动,满足mag=qE,可得E=10N/C。
重力竖直向下,静电力竖直向上,而a球带正电,故电场强度方向竖直向上。
(2)规定水平向左为正方向,a球与b球发生弹性正碰,由动量守恒定律得mava=mav0+mbvb﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①
由能量守恒定律得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②
解得v0=0.3m/s,vb=1.2m/s。﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣③
(3)对a球,洛伦兹力提供向心力﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣④
可得r==0.30m﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑤
设a球落地点与球心的连线和地面夹角为θ,由几何关系有h=r+rsinθ,则θ=
故a球在电磁场中运动的时间,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑥
解得﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑦
b球不带电,碰撞后做平抛运动,竖直方向有﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑧
解得tb=0.30s﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣⑨
答:
(1)电场强度为10N/C,方向竖直向上。
(2)碰后瞬间a球的速度0.3m/s,b球的速度为1.2m/s。
(3)碰后a球在磁场中运动时间为,b球在磁场中运动时间为0.30s。
三.多选题(共2小题,满分15分)
13.(5分)下列说法正确的是( )
A.一切晶体的光学和力学性质都是各向异性的
B.在完全失重的宇宙飞船中,水的表面存在表面张力
C.当分子间的距离变小时,分子间作用力的合力可能减小,也可能增大
D.一切与热现象有关的宏观自然过程都是可逆的
E.脱脂棉脱脂的目的在于使它从不能被水浸润变为可以被水浸润,以便吸取药液
【解答】解:A、一切单晶体的物理性质具有各向异性,但多晶体具有各向同性,故A错误;
B、由于液体的蒸发,液体表面分子较为稀疏,故分子间距大于液体内部,表现为引力,分子力与重力无关,故在完全失重的宇宙飞船中,水的表面依然存在表面张力,故B正确;
C、当分子间距离r<r0时,分子间表现为斥力,若分子间距离减小,斥力增大。当r>r0时,分子间表现为引力,分子间距离减小时,分子力可能减小,故C正确;
D、一切与热现象有关的宏观自然过程都具有方向性,是不可逆的,故D错误;
E、脱脂棉能够吸取药液,在于脱脂后把它从不能被水浸润变成了可以被水浸润,故E正确。
故选:BCE。
14.(10分)如图所示,体积为V0的导热容器被一光滑导热活塞C(厚度忽略不计)分成A、B两个气室,各封闭一定质量的气体,平衡时B室的体积是A室体积的三倍,A室容器上连接有一管内气体体积不计的足够长U形管,两侧水银柱高度差为76cm,B室容器可通过一阀门K与大气相通。已知外界大气压p0=76cmHg,环境温度T0=300K。
(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是多少?
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,求此时A室内气体压强。
【解答】解:(ⅰ)开始时,A室内的气体压强为:pA0=p0+ρgh=2p0,A室内的气体体积为:VA0=
打开阀门,A室气体等温变化,稳定后压强为:pA1=p0,体积为VA1
对A室气体,由玻意耳定律得:pA0VA0=pA1VA1
解得:VA1=
B室气体等温变化,稳定后压强为:pB0=pA0,pB1=pA1,VB0=V0﹣VA0=
对B室气体,由玻意耳定律得:pB0VB0=pB1VB1
解得:VB1=
则稳定后B室内剩余气体的质量和B室原有气体质量之比为:===
(ⅱ)假设打开阀门后,气体从T0=300K升到T时,活塞C恰好到达容器最右端,即气体体积变为V0,压强pA仍为p0,即等压变化过程,
则根据盖一吕萨克定律,有=
解得:T1=600K
因为T2=750K>600K,所以温度从T1=600K升高到T2=750K,是等容变化过程,
根据查理定律,有=
代入数据解得此时A室内气体压强为:pA2=95cmHg
答:(ⅰ)环境温度保持不变,将阀门K打开,稳定后B室内剩余气体的质量和B室原有气体质量之比是;
(ⅱ)打开阀门K稳定后,将环境温度缓慢升高到750K,此时A室内气体压强为95cmHg。
四.填空题(共2小题)
15.图甲为一列沿x轴方向传播的简谐横波在t=1时的波形图,P、Q是平衡位置在xp=1m、xQ=2.5m处的两个质点,图乙为质点为P的振动图象。质点P的振动方程为y= 4cos cm(用余弦函数表示);从t=1s时开始,质点Q第一次回到平衡位置所需的时间为 1.5 s。
【解答】解:根据图乙可得P的振动为余弦图象,则y=Acosωt=4cos=4cos cm;
t=1s时P向下振动,根据“同侧法”可知该波向右传播,波速v=m/s=1m/s
质点Q第一次回到平衡位置所需的时间为t==s=1.5s。
故答案为:4cos;1.5。
16.如图所示为某种透明材料制成的棱镜的横截面图,ABOD为矩形,CD是半径为R的四分之一圆弧,圆心为O;一束平行光线从AB上射入,入射角为θ,其中从M点入射的光线进入棱镜后恰好在BC上的O点发生全反射,然后由CD射出。已知OB段的长度为L,真空中的光速为c。求:
(i)该透明材料的折射率n;
(ii)若透明材料的折射率n=,L=R,不考虑光在CD上的反射,求能从CD上射出的光线对应的圆心角α。
【解答】解:(1)设光线在AB面的折射角为r,光路如图所示。
根据折射定律得:n=
设棱镜的全反射临界角为θC,由题意知,光线在BC面上的O点恰好发生全反射,入射角等于临界角,则
sinθC=
由几何知识可知:r+θC=90°。
联立以上各式解得:n=;
(ii)若透明材料的折射率n=,由sinθC=解得θC=60°
由r+θC=90°,得r=30°
设刚好在O点发生全反射的光线从CD上的P点射出,由A和B处入射的边界光线分别能到达CD圆弧上的C′点和D′点,在AB上发生折射后直接到达CD上的光线,在C′处与法线间的夹角最大。
则在三角形OEC′中,由正弦定理得
=
由几何关系知∠OEC′=60°,OE<R,则β<60°
故由AB上发生折射后直接射到CD圆弧上的光线不会在CD上发生全反射。
经分析,从AB折射后到达BC经过全反射到达CD圆弧上CP间的光线,在C点处与法线间的夹角最大,且为30°,故不会在CD上发生全反射,CP间有光线从CD上射出。
从AB折射到达BC经过全反射后到达CD圆弧上PD′间的光线在D′射出时与光线间的夹角最大,设到达D′点的光线与OD′间的夹角为θ′,如图2所示,则在三角形OBD′中,由正弦定理得
=
解得sinθ′==
故θ′<60°
光线也不会在CD上发生全反射,故有光线从CD上射出的圆弧范围为CD′,由几何知识得OD′与法线OC间的夹角α=30°+θ′,其中θ′=arcsin。
答:(i)该透明材料的折射率n是;
(ii)能从CD上射出的光线对应的圆心角α是30°+arcsin。
同课章节目录
