安徽省芜湖市2021-2022学年高三上学期期末物理模拟试卷(1)(Word版含答案)
文档属性
| 名称 | 安徽省芜湖市2021-2022学年高三上学期期末物理模拟试卷(1)(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 512.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-06 14:30:07 | ||
图片预览




文档简介
2021-2022学年安徽省芜湖市高三(上)期末物理模拟试卷(1)
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)2020年3月20日,电影《放射性物质》在伦敦首映,该片的主角﹣﹣居里夫人是放射性元素钋(Po)的发现者。钋210的半衰期是138天;钋210核发生衰变时,会产生α粒子和原子核X,并放出γ射线。下列说法正确的是( )
A.γ射线是高速电子流
B.原子核X的中子数为82
C.10个钋210核经过138天,一定还剩下5个钋核
D.衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量
2.(6分)某短跑运动员完成100m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1:4,则该运动员在加速阶段的加速度为( )
A.2.0m/s2 B.2.5m/s2 C.3.0m/s2 D.3.5m/s2
3.(6分)满载A国公民的一航班在飞行途中神秘消失,A国推断航班遭到敌对国家劫持,政府立即调动大量海空军事力量进行搜救,并在第一时间紧急调动了21颗卫星参与搜寻,“调动”卫星的措施之一就是减小卫星环绕地球运动的轨道半径,降低卫星运行的高度,以有利于发现地面(或海洋)目标,下面说法正确的是( )
A.轨道半径减小后,卫星的环绕重力势能增大
B.轨道半径减小后,卫星的环绕速度增大
C.轨道半径减小后,卫星的环绕机械能增大
D.轨道半径减小后,卫星的环绕周期增大
4.(6分)如图所示,在高度不同的两水平台阶上放有质量分别为m1、m2的两物体A、B,物体间用轻弹簧相连,弹簧与竖直方向夹角为θ.在物体A左端施加水平拉力F,使A、B均处于静止状态,已知物体A表面光滑,重力加速度为g,则下列说法正确的是( )
A.弹簧弹力的大小为
B.m1与m2一定相等
C.地面对B的支持力可能为零
D.地面对B的摩擦力大小为F
5.(6分)如图所示,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧轨道,BC段是长为L的粗糙水平轨道,两段轨道相切于B点。一质量为m、可视为质点的滑块从小车上的A点由静止开始沿轨道下滑,然后滑入BC轨道,最后恰好停在C点。已知小车质量M=4m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g,则( )
A.全过程滑块在水平方向上相对地面的位移的大小为R+L
B.小车在运动过程中速度的最大值为
C.全过程小车相对地面的位移大小为
D.μ、L、R三者之间的关系为R=μL
6.(6分)利用霍尔元件可以进行微小位移的测量,而半导体是制作霍尔元件的重要材料,若其中的载流子带正电,则成为P型半导体,若其中的载流子带负电,则称为N型半导体。如图甲所示,将固定有一个带有由P型半导体制成的霍尔元件的物体置于两块磁性强弱相同、同极相对放置的磁体缝隙中,建立如图乙所示的空间坐标系。保持沿x方向通过霍尔元件的电流I不变,当物体沿z轴方向移动时,由于不同位置处磁感应强度B不同,霍尔元件将在y轴方向的上、下表面间产生不同的霍尔电压UH。当用霍尔元件处于中间位置时,磁感应强度B为0,UH为0,将该点作为位移的零点。现将一个电压表并联在霍尔元件的两端,当霍尔元件的位置坐标为z=z0>0时,电压表的示数U=U0>0。已知在小范围内,磁感应强度B的大小和坐标z成正比,这样就可以把电压表当成测量物体微小位移的仪表。下列说法中正确的是( )
A.保持其他条件不变,仅换用由N型半导体制成的霍尔元件,则有z=z0时,U=﹣U0
B.保持其他条件不变,仅将两磁体的放置方向变为两S极,则有z=z0时,U=﹣U0
C.保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,U=U0
D.保持其他条件不变,仅减小霍尔元件沿y轴方向的厚度,则可以提高测量的精确度
7.(6分)如图,边界OM与ON间有垂直纸面向里的匀强磁场磁感应强度为B。边界ON上有一粒子源S,沿平行于纸面向磁场内各个方向发射大量带电荷量为+q、质量为m的相同速率的同种粒子,其中部分粒子能从边界OM射出磁场。已知∠MON=30°,OS=d,且从OM射出的粒子在磁场中运动的最短时间为。不考虑粒子间的相互作用,则( )
A.粒子的速率为
B.粒子的速率为
C.从OM射出的粒子,射出时与O点的最远距离为2d
D.从OM射出的粒子,射出时与O点的最远距离为d
8.(6分)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑。现将一质量为m、带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
A.小球释放后,到达最低点D时速度最大
B.小球释放后,到达B点时速度为零,并在BDA间往复运动
C.小球第一次经过最低点D和最高点C时对管壁的压力大小之比为5:1
D.小球第一次和第二次经过最高点C时对管壁的压力大小之比为1:3且方向相同
二.实验题(共4小题,满分47分)
9.(5分)(1)甲、乙、丙三个实验小组分别采用如图(甲)、(乙)、(丙)所示的实验装置,验证“当质量一定时,物体运动的加速度与它所受的合力成正比”这一物理规律。已知他们使用的小车完全相同,小车的质量为M,重物的质量为m,试回答下列问题:
①甲、乙、丙实验中,必须平衡小车和长木板之间的摩擦力的实验小组是 。
A.甲、乙、丙
B.甲、乙
C.甲、丙
②实验时,必须满足“M远大于m”的实验小组是 (填:甲、乙、丙)。
③实验时,甲、丙两组同学的操作均完全正确,他们作出的a﹣F图线如图(丁)中B、C所示,则甲、丙两组实验对应的图线依次是 。
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,以弹簧测力计的示数F为横坐标,加速度a为纵坐标,画出的a﹣F图线是如图(丁)中A为一条直线。测出图线与横坐标的夹角为θ;求得图线的斜率为k。则小车的质量为 。
A.
B.
C.
D.k
10.(10分)用伏安法测定一个待测电阻Rx的阻值(阻值约为150Ω),实验室提供如下器材:
电源E:电动势为2V,内阻不计;
电流表A1:量程0~15mA,内阻约为50Ω;
电流表A2:量程0~300μA,内阻为800Ω;
滑动变阻器R1:阻值范围0~10Ω,额定电流2A;
电阻箱R2:阻值范围0~9999Ω,额定电流1A;
开关S、导线若干。
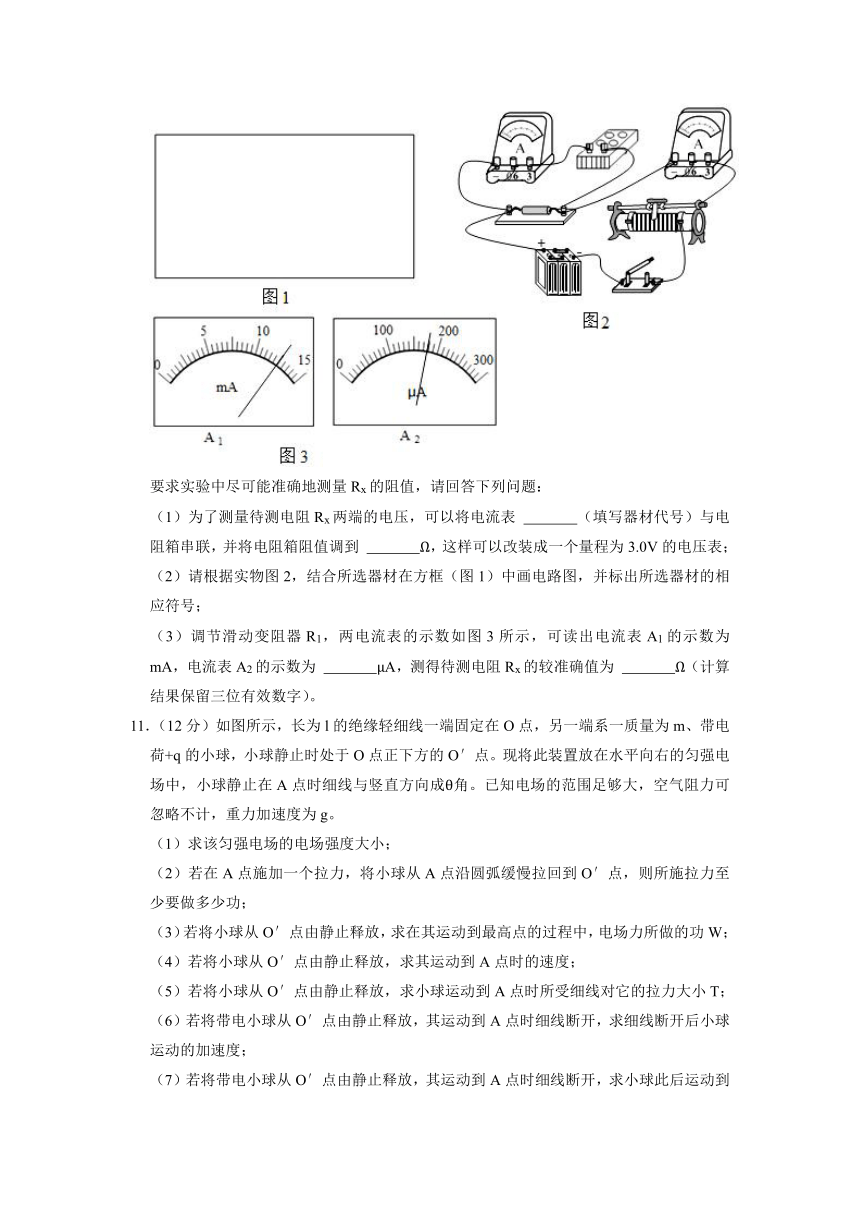
要求实验中尽可能准确地测量Rx的阻值,请回答下列问题:
(1)为了测量待测电阻Rx两端的电压,可以将电流表 (填写器材代号)与电阻箱串联,并将电阻箱阻值调到 Ω,这样可以改装成一个量程为3.0V的电压表;
(2)请根据实物图2,结合所选器材在方框(图1)中画电路图,并标出所选器材的相应符号;
(3)调节滑动变阻器R1,两电流表的示数如图3所示,可读出电流表A1的示数为 mA,电流表A2的示数为 μA,测得待测电阻Rx的较准确值为 Ω(计算结果保留三位有效数字)。
11.(12分)如图所示,长为l的绝缘轻细线一端固定在O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O点正下方的O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。已知电场的范围足够大,空气阻力可忽略不计,重力加速度为g。
(1)求该匀强电场的电场强度大小;
(2)若在A点施加一个拉力,将小球从A点沿圆弧缓慢拉回到O′点,则所施拉力至少要做多少功;
(3)若将小球从O′点由静止释放,求在其运动到最高点的过程中,电场力所做的功W;
(4)若将小球从O′点由静止释放,求其运动到A点时的速度;
(5)若将小球从O′点由静止释放,求小球运动到A点时所受细线对它的拉力大小T;
(6)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求细线断开后小球运动的加速度;
(7)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求小球此后运动到最高点时的速度大小;
(8)若小球在A点附近小角度(小于5°)往复运动,求它从A点出发后到第二次再通过A点的过程中所经历的时间。
12.(20分)如图所示,一倾角为θ的固定斜面底端安装一挡板,物块Q静止在与挡板相距为s(足够大)的A处。某时刻,物块P以沿斜面向下的速度v0与Q发生弹性碰撞,已知Q与斜面间的动摩擦因数为2tanθ,最大静摩擦力等于滑动摩擦力,P与斜面间无摩擦,两物块(视为质点)质量均为m,取重力加速度为g。
(1)求P与Q第一次碰撞后瞬间各自的速度大小;
(2)求P与Q第二次碰撞前瞬间各自的速度大小;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,求Q停止的位置与挡板的距离。
三.多选题(共2小题,满分15分)
13.(5分)如图所示,电路与一绝热密闭气缸相连,R为电阻丝,气缸内有一定质量的理想气体,外界大气压恒定。闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法正确的是( )
A.气体的内能增加
B.气体分子平均动能不变
C.气体的压强不变
D.气体分子对容器器壁碰撞的次数减小了
E.电热丝放出的热量等于气体对外所做的功
14.(10分)如图所示,两端开口内壁光滑的导热汽缸竖直固定放置,质量分别为m和2m的两个活塞A、B由长度为2L的轻杆相连,两活塞的横截面积分别为S和2S,活塞间封闭有一定质量的理想气体。开始时,活塞B距离较细汽缸底端为L,整个装置处于静止状态。此时大气压强为p0=,汽缸周围温度为127℃,现在活塞A上部缓慢倒入细沙,直到活塞A恰好位于较细气缸底部。重力加速度为g。
(1)求加入细沙的质量;
(2)保持细沙质量不变,再缓慢降低气体温度,使活塞回到原来位置,内能减少了△U,求此时封闭气体的温度及此过程中气体放出的热量。
四.填空题(共2小题)
15.一列简谐横波沿x轴传播,t=0时刻波刚传到x=2.5m处,其波形如图甲所示。P、Q为介质中两个质点,其平衡位置xp=0.5m,xQ=5m,图乙是质点P的振动图像。则该简谐横波的波速为 m/s;10s内Q质点通过的路程为 cm。
16.如图所示,ABC为一玻璃棱镜的截面,该截面是由半径为R的圆弧的一部分和一直角三角形组成的,O点为圆心,R=20cm,∠AOB=60°,折射率n=2,一束平行光垂直于AB面射入玻璃棱镜。求:
(1)光线由该棱镜材料射向空气时发生全反射的临界角;
(2)BC面上有光线逸出部分的弧长。
2021-2022学年安徽省芜湖市高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)2020年3月20日,电影《放射性物质》在伦敦首映,该片的主角﹣﹣居里夫人是放射性元素钋(Po)的发现者。钋210的半衰期是138天;钋210核发生衰变时,会产生α粒子和原子核X,并放出γ射线。下列说法正确的是( )
A.γ射线是高速电子流
B.原子核X的中子数为82
C.10个钋210核经过138天,一定还剩下5个钋核
D.衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量
【解答】解:A、γ射线的实质是频率很高的电磁波,不是电子流,故A错误;
B、根据发生核反应时,质量数与电荷数守恒,可得原子核X的质子数为:84﹣2=82,质量数为:210﹣4=206,依据质量数等于质子数与中子数之和,得原子核X的中子数为206﹣82=124,故B错误;
C、半衰期是大量放射性元素的原子核中有一半发生衰变的时间,对个别的放射性原子核没有意义,故C错误;
D、由于衰变的过程中释放能量,根据质能方程可知存在质量亏损,所以衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量,故D正确。
故选:D。
2.(6分)某短跑运动员完成100m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1:4,则该运动员在加速阶段的加速度为( )
A.2.0m/s2 B.2.5m/s2 C.3.0m/s2 D.3.5m/s2
【解答】解:设运动员加速时间为t1,匀速时间为t2,匀速运动的速度为v,
加速的位移为:x1=t1
匀速的位移:x2=vt2
x1+x2=100m
x1:x2=1:4
解得:t1=4s,t2=8s,
x1=20m,x2=80m,
匀加速阶段,根据位移时间公式:
x1=
解得:a=2.5m/s2
故B正确;ACD错误。
故选:B。
3.(6分)满载A国公民的一航班在飞行途中神秘消失,A国推断航班遭到敌对国家劫持,政府立即调动大量海空军事力量进行搜救,并在第一时间紧急调动了21颗卫星参与搜寻,“调动”卫星的措施之一就是减小卫星环绕地球运动的轨道半径,降低卫星运行的高度,以有利于发现地面(或海洋)目标,下面说法正确的是( )
A.轨道半径减小后,卫星的环绕重力势能增大
B.轨道半径减小后,卫星的环绕速度增大
C.轨道半径减小后,卫星的环绕机械能增大
D.轨道半径减小后,卫星的环绕周期增大
【解答】解:A、卫星轨道半径减小,卫星离地面高度降低,卫星的重力势能减小,故A错误;
B、据可知,卫星的线速度v=,可知当轨道半径减小后,卫星的环绕速度v增大,故B正确;
C、卫星减小轨道半径时,需要减速做近心运动,在同一位置减速时,势能不变动能减小,卫星的机械能减小,故轨道半径减小后,卫星的环绕机械能减小,故C错误;
D、据可知,卫星的环绕周期T=,卫星轨道半径减小后,卫星的环绕周期减小,故D错误。
故选:B。
4.(6分)如图所示,在高度不同的两水平台阶上放有质量分别为m1、m2的两物体A、B,物体间用轻弹簧相连,弹簧与竖直方向夹角为θ.在物体A左端施加水平拉力F,使A、B均处于静止状态,已知物体A表面光滑,重力加速度为g,则下列说法正确的是( )
A.弹簧弹力的大小为
B.m1与m2一定相等
C.地面对B的支持力可能为零
D.地面对B的摩擦力大小为F
【解答】解:D、对整体受力分析可知,整体受重力、支持力、拉力;要使整体处于平衡,则水平方向一定有向右的摩擦力作用在m2上,且大小与F相同;故D正确;
C、因m2与地面间有摩擦力;则一定有支持力;故C错误;
A、再对m2受力分析可知,弹力水平方向的分力应等于F,故弹力T=,故A错误;
B、因竖直方向上的受力不明确,无法确定两物体的质量关系;也无法求出弹簧弹力与重力的关系;故B错误;
故选:D。
5.(6分)如图所示,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧轨道,BC段是长为L的粗糙水平轨道,两段轨道相切于B点。一质量为m、可视为质点的滑块从小车上的A点由静止开始沿轨道下滑,然后滑入BC轨道,最后恰好停在C点。已知小车质量M=4m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g,则( )
A.全过程滑块在水平方向上相对地面的位移的大小为R+L
B.小车在运动过程中速度的最大值为
C.全过程小车相对地面的位移大小为
D.μ、L、R三者之间的关系为R=μL
【解答】解:AC、设全过程滑块相对地面的位移大小为x,则小车相对地面位移大小为s=R+L﹣x,
滑块与小车组成的系统在水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得:
mv滑块﹣Mv小车=0,则m﹣M=0,由题意可知:M=4m,解得:x=,s=,故A错误,C正确;
B、滑块到达B点时小车速度最大,滑块在圆弧轨道下滑过程系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得:
mv滑块﹣Mv小车=0
由机械能守恒定律得:mgR=
解得:v小车=,故B正确;
D、滑块恰好停在C点,由能量守恒定律得:mgR=μmgL,解得:R=μL,故D正确。
故选:BCD。
6.(6分)利用霍尔元件可以进行微小位移的测量,而半导体是制作霍尔元件的重要材料,若其中的载流子带正电,则成为P型半导体,若其中的载流子带负电,则称为N型半导体。如图甲所示,将固定有一个带有由P型半导体制成的霍尔元件的物体置于两块磁性强弱相同、同极相对放置的磁体缝隙中,建立如图乙所示的空间坐标系。保持沿x方向通过霍尔元件的电流I不变,当物体沿z轴方向移动时,由于不同位置处磁感应强度B不同,霍尔元件将在y轴方向的上、下表面间产生不同的霍尔电压UH。当用霍尔元件处于中间位置时,磁感应强度B为0,UH为0,将该点作为位移的零点。现将一个电压表并联在霍尔元件的两端,当霍尔元件的位置坐标为z=z0>0时,电压表的示数U=U0>0。已知在小范围内,磁感应强度B的大小和坐标z成正比,这样就可以把电压表当成测量物体微小位移的仪表。下列说法中正确的是( )
A.保持其他条件不变,仅换用由N型半导体制成的霍尔元件,则有z=z0时,U=﹣U0
B.保持其他条件不变,仅将两磁体的放置方向变为两S极,则有z=z0时,U=﹣U0
C.保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,U=U0
D.保持其他条件不变,仅减小霍尔元件沿y轴方向的厚度,则可以提高测量的精确度
【解答】解:P型半导体在z=z0>0区域,磁场方向向左,电流沿x方向,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,P型半导体载流子带正电,故上表面电势高,因测的U=U0>0,故半导体上表面接电压表正极。
A、保持其他条件不变,换用由N型半导体制成的霍尔元件,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,N型半导体载流子带负电,故上表面电势低,因半导体上表面接电压表正极,故电压表示数为﹣U0,故A正确;
B、保持其他条件不变,仅将两磁体的放置方向变为两S极,磁场方向变为向右,应用左手定则可判断出载流子向y轴负方向移动,即向半导体下表面移动,P型半导体载流子带正电,故下表面电势高,因半导体上表面接电压表正极,故电压表示数为﹣U0,故B正确;
C、保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,磁场方向变为向右,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,P型半导体载流子带正电,故上表面电势高,因半导体上表面接电压表正极,故电压表示数为U0,故C正确;
D、设y轴方向的厚度为d,沿z轴方向的厚度为b,达到稳定后有,又I=nqSv=nqbdv,联立得:U=,即U与d无关系,故D错误;
故选:ABC。
7.(6分)如图,边界OM与ON间有垂直纸面向里的匀强磁场磁感应强度为B。边界ON上有一粒子源S,沿平行于纸面向磁场内各个方向发射大量带电荷量为+q、质量为m的相同速率的同种粒子,其中部分粒子能从边界OM射出磁场。已知∠MON=30°,OS=d,且从OM射出的粒子在磁场中运动的最短时间为。不考虑粒子间的相互作用,则( )
A.粒子的速率为
B.粒子的速率为
C.从OM射出的粒子,射出时与O点的最远距离为2d
D.从OM射出的粒子,射出时与O点的最远距离为d
【解答】解:AB、粒子在磁场中运动做匀速圆周运动,入射点是S,出射点在OM直线上,出射点与S点的连线为轨迹的一条弦。当从边界OM射出的粒子在磁场中运动的时间最短时,轨迹的弦最短,即通过S点做OM的垂线SC为最短的弦,如图所示;
且
所以θ==120°,则弦切角为60°
由几何关系有:SC=2Rsin60° 而SC=d×sin30°
由洛伦兹力提供向心力可得qvB=m ,解得:R=
联立可得:v=,故A错误,B正确;
CD、若最远点为D点,当SD为轨迹圆的直径时D点离O最远,由几何关系知,△ODS是直角三角形,那么:SD==,故C错误,D正确。
故选:BD。
8.(6分)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑。现将一质量为m、带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
A.小球释放后,到达最低点D时速度最大
B.小球释放后,到达B点时速度为零,并在BDA间往复运动
C.小球第一次经过最低点D和最高点C时对管壁的压力大小之比为5:1
D.小球第一次和第二次经过最高点C时对管壁的压力大小之比为1:3且方向相同
【解答】解:A、如图所示合力与重力的夹角满足tanθ==1,即θ=45°,当小球重力和电场力的合力正好沿半径方向时,小球的速度最大,所以速度最大点在D点的左侧,故A错误;
B、只有重力和电场力做功,带电小球到达B点,重力势能不变,电势能减小,故有动能,其动能大小等于电场力做的功,为qE 2R=,故B错误;
C、第一次过D点时,
根据动能定理可知:mgR+qER=m,
由牛顿第二定律可知:N1D﹣mg=m,
又由于qE=mg
故解得N1D=5mg
第一次过C点,
由牛顿第二定律可知:N1C+mg=m,
根据动能定理可知:2EqR﹣mgR=m,
又由于qE=mg
故解得N1C=mg,故C正确;
D、从A点释放到第二次到C点过程,
根据动能定理可知:﹣mgR+2qE 2R=mv2C2
在C点牛顿第二定律可知:N2C+mg=m
解得N2C=5mg,
故:N1C:N2C=1:5,故D错误;
故选:C。
二.实验题(共4小题,满分47分)
9.(5分)(1)甲、乙、丙三个实验小组分别采用如图(甲)、(乙)、(丙)所示的实验装置,验证“当质量一定时,物体运动的加速度与它所受的合力成正比”这一物理规律。已知他们使用的小车完全相同,小车的质量为M,重物的质量为m,试回答下列问题:
①甲、乙、丙实验中,必须平衡小车和长木板之间的摩擦力的实验小组是 A 。
A.甲、乙、丙
B.甲、乙
C.甲、丙
②实验时,必须满足“M远大于m”的实验小组是 甲 (填:甲、乙、丙)。
③实验时,甲、丙两组同学的操作均完全正确,他们作出的a﹣F图线如图(丁)中B、C所示,则甲、丙两组实验对应的图线依次是 CB 。
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,以弹簧测力计的示数F为横坐标,加速度a为纵坐标,画出的a﹣F图线是如图(丁)中A为一条直线。测出图线与横坐标的夹角为θ;求得图线的斜率为k。则小车的质量为 C 。
A.
B.
C.
D.k
【解答】解:(1)①(甲)、(乙)、(丙)三个图小车与长木板之间都有摩擦力,为保证小车受到的拉力就是所受的合力,所以都需要平衡摩擦力,故A正确,BC错误;
故选:A
②(乙)、(丙)两图绳上的力由弹簧测力计和力传感器直接读出,不需要用重物的重力代替,所以不需满足M m;(甲)图用重物的重力代替绳的拉力,必须满足M m;
③(甲)图用重物的重力代替绳子的拉力,需满足M m,随着m的增大,不满足M m时,图象出现弯曲,所以甲组对应的是C;(乙)、(丙)图根据拉力相等时,加速度a乙>a丙,从而判断乙组对应A,丙组对应B。故答案为:CB;
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,对小车由牛顿第二定律得:2F=Ma
以弹簧测力计的示数F为横坐标,加速度a为纵坐标,整理得:a=F,根据图线的斜率为k=,解得小车的质量为:M=,故C正确,ABD错误,
故选:C。
故答案为:(1)①A、②甲、③CB;(2)C
10.(10分)用伏安法测定一个待测电阻Rx的阻值(阻值约为150Ω),实验室提供如下器材:
电源E:电动势为2V,内阻不计;
电流表A1:量程0~15mA,内阻约为50Ω;
电流表A2:量程0~300μA,内阻为800Ω;
滑动变阻器R1:阻值范围0~10Ω,额定电流2A;
电阻箱R2:阻值范围0~9999Ω,额定电流1A;
开关S、导线若干。
要求实验中尽可能准确地测量Rx的阻值,请回答下列问题:
(1)为了测量待测电阻Rx两端的电压,可以将电流表 A2 (填写器材代号)与电阻箱串联,并将电阻箱阻值调到 9200 Ω,这样可以改装成一个量程为3.0V的电压表;
(2)请根据实物图2,结合所选器材在方框(图1)中画电路图,并标出所选器材的相应符号;
(3)调节滑动变阻器R1,两电流表的示数如图3所示,可读出电流表A1的示数为 12.5 mA,电流表A2的示数为 180 μA,测得待测电阻Rx的较准确值为 146 Ω(计算结果保留三位有效数字)。
【解答】解:(1)由于题目没有给电压表,为测电压可以将已知内阻的电流表A2与电阻箱串联改装成电压表测电压,
由欧姆定律可知,把电流表改装成U=3.0V的电压表串联电阻阻值R===9200Ω;
(2)根据图示实物电路图作出实验电路图,实验电路图如图所示:
(3)电流表A1的量程是15mA,分度值是0.5mA,示数I1=12.5mA,
电流表A2的量程是300μA,分度值是10μA,而I2=180μA,
由欧姆定律可知,待测电阻阻值:Rx==Ω=146Ω。
故答案为:(1)A2;9200;(2)电路图如图所示;(3)12.5;180;146。
11.(12分)如图所示,长为l的绝缘轻细线一端固定在O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O点正下方的O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。已知电场的范围足够大,空气阻力可忽略不计,重力加速度为g。
(1)求该匀强电场的电场强度大小;
(2)若在A点施加一个拉力,将小球从A点沿圆弧缓慢拉回到O′点,则所施拉力至少要做多少功;
(3)若将小球从O′点由静止释放,求在其运动到最高点的过程中,电场力所做的功W;
(4)若将小球从O′点由静止释放,求其运动到A点时的速度;
(5)若将小球从O′点由静止释放,求小球运动到A点时所受细线对它的拉力大小T;
(6)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求细线断开后小球运动的加速度;
(7)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求小球此后运动到最高点时的速度大小;
(8)若小球在A点附近小角度(小于5°)往复运动,求它从A点出发后到第二次再通过A点的过程中所经历的时间。
【解答】解:(1)对带电小球受力分析如图所示,可得:tanθ=,解得:E=
(2)根据动能定理可知:WF+mgl(1﹣cosθ)﹣qElsinθ=0,解得:WF=
(3)根据对称性可知,小球摆到最高点时摆线与竖直方向夹角为2θ,则电场力做功为:W=Eqlsin2θ=mgtanθ lsin2θ=2mglsin2θ
(4)从O′点到A点,动能定理:qElsinθ﹣mgl(1﹣cosθ)=,解得:,方向与水平方向成θ角斜向上
(5)在A点由牛顿第二定律:T﹣mgcosθ=,解得:T=mg()
(6)到A点时细绳断开,则此时小球受向下的重力和向右的电场力,其合力为:
由牛顿第二定律可知:a===,方向与竖直方向成θ角斜向下。
(7)运动到A点时细绳断开,小球此后在水平方向做匀加速运动,水平初速度为:vx0=vAcosθ,水平加速度为:ax=asinθ
竖直方向做匀减速运动,竖直初速度为:vy0=vAsinθ,竖直加速度为:ay=acosθ
运动到最高点所用的时间为:t==
则水平速度即为最高点的速度:vx=vx0+axt=vAcosθ+asinθ =
(8)若小球在A点附近小角度往复运动,则可看做单摆模型,周期T=,其等效重力加速度为:,那么周期化简得:T=
它从A点出发后到第二次再通过A点的过程中所经历的时间为一个周期,则时间t=T=
答:(1)匀强电场的电场强度大小为:;
(2)拉力至少要做的功为:;
(3)电场力做功W=2mglsin2θ;
(4)运动到A点速度大小为,方向与水平方向成θ角斜向上;
(5)小球运动到A点所受细绳对它的拉力T=;
(6)细绳断开后小球运动的加速度大小为,方向与竖直方向成θ角斜向下;
(7)小球运动到最高点时的速度大小为;
(8)小球从A点出发后到第二次再通过A点的过程中所经历的时间为。
12.(20分)如图所示,一倾角为θ的固定斜面底端安装一挡板,物块Q静止在与挡板相距为s(足够大)的A处。某时刻,物块P以沿斜面向下的速度v0与Q发生弹性碰撞,已知Q与斜面间的动摩擦因数为2tanθ,最大静摩擦力等于滑动摩擦力,P与斜面间无摩擦,两物块(视为质点)质量均为m,取重力加速度为g。
(1)求P与Q第一次碰撞后瞬间各自的速度大小;
(2)求P与Q第二次碰撞前瞬间各自的速度大小;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,求Q停止的位置与挡板的距离。
【解答】解:(1)PQ组成的系统,在第一次碰撞过程中,沿斜面方向根据动量守恒可得:mv0=mvP1+mvQ1
在第一次碰撞过程中,PQ组成的系统,根据能量守恒可得:
联立解得:vp1=0,vQ1=v0
(2)对Q受力分析可知:μmgcosθ﹣mgsinθ=maQ
解得aQ=gsinθ
Q匀减速运动,则
度P受力分析可知mgsinθ=maP,解得aP=gsinθ
P匀加速直线运动,
碰撞条件为xP=xQ,
解得t=
v′P=aPtv′Q=v0﹣aQt
解得:v′P=v0,v′Q=0
(3)任意两次碰撞位置的距离L=
PQ最后一次碰撞的位置与挡板距离x=s﹣nL
其中n为结果的整数部分
PQ最后一次碰撞后,Q运动至挡板出由
于是Q与挡板碰撞前速度
Q与挡板碰撞前后有:
Q反弹的速度
Q沿斜面上升过程
于是:Q停下位置距挡板△x=,其中n为的整数部分
答:(1)P与Q第一次碰撞后瞬间各自的速度大小分别为0和v0;
(2)求P与Q第二次碰撞前瞬间各自的速度大小分别为v0和0;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,Q停止的位置与挡板的距离,其中n为的整数部分
三.多选题(共2小题,满分15分)
13.(5分)如图所示,电路与一绝热密闭气缸相连,R为电阻丝,气缸内有一定质量的理想气体,外界大气压恒定。闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法正确的是( )
A.气体的内能增加
B.气体分子平均动能不变
C.气体的压强不变
D.气体分子对容器器壁碰撞的次数减小了
E.电热丝放出的热量等于气体对外所做的功
【解答】解:AB、闭合电键后,给气体加热,温度升高,分子平均动能增大,内能增大,故A正确,B错误。
C、以活塞为研究对象,根据平衡条件知,密闭气体的压强等于外界大气压强,所以密闭气体压强不变,故C正确。
D、根据气体压强的微观意义,气体压强和单位时间对器壁单位面积的碰撞次数、分子平均动能有关;现气体压强不变,分子平均动能增大,则气体分子单位时间对器壁单位面积的碰撞次数减小,故D正确。
E、内能增大,△U>0,体积增大,气体对外做功,W<0,根据热力学第一定律△U=Q+W,有Q>0,则Q>﹣W>0,即电热丝放出的热量大于气体对外所做的功,故E错误。
故选:ACD。
14.(10分)如图所示,两端开口内壁光滑的导热汽缸竖直固定放置,质量分别为m和2m的两个活塞A、B由长度为2L的轻杆相连,两活塞的横截面积分别为S和2S,活塞间封闭有一定质量的理想气体。开始时,活塞B距离较细汽缸底端为L,整个装置处于静止状态。此时大气压强为p0=,汽缸周围温度为127℃,现在活塞A上部缓慢倒入细沙,直到活塞A恰好位于较细气缸底部。重力加速度为g。
(1)求加入细沙的质量;
(2)保持细沙质量不变,再缓慢降低气体温度,使活塞回到原来位置,内能减少了△U,求此时封闭气体的温度及此过程中气体放出的热量。
【解答】解:(1)设初始状态封闭气体的压强为p1,
对活塞整体,由平衡条件可得:p0S+p1×2S+3mg=p0×2S+p1S
设活塞A到达气缸底部时封闭气体的压强为p2、加入细沙的质量为m0,
对活塞与细沙整体,由平衡条件得:p0S+p2×2S+3mg+m0g=p0×2S+p2S
根据玻意耳定律得:p1(LS+2LS)=p2×2L×2S
解得:m0=0.5m
(2)降低温度过程中气体做等压变化,
由盖﹣吕萨克定律得:
代入数据解得:T2=300K
体积恢复过程中外界对气体做的功:W=p2LS
解得:W=1.5mgL
由热力学第一定律得:﹣△U=W﹣Q
解得:Q=1.5mgL+△U
答:(1)加入细沙的质量是0.5m;
(2)此时封闭气体的温度是300K,此过程中气体放出的热量是1.5mgL+△U。
四.填空题(共2小题)
15.一列简谐横波沿x轴传播,t=0时刻波刚传到x=2.5m处,其波形如图甲所示。P、Q为介质中两个质点,其平衡位置xp=0.5m,xQ=5m,图乙是质点P的振动图像。则该简谐横波的波速为 1 m/s;10s内Q质点通过的路程为 75 cm。
【解答】解:根据甲图知波长为:λ=2m,根据乙图知周期为:T=2s
所以波速为:=;
机械波传到Q点需要的时间为:
所以Q点振动的时间为:t2=10s﹣2.5s=7.5s
10s内Q质点通过的路程为:
从图中可以读出振幅为:A=5cm
所以:s=15A=15×5cm=75cm.
故答案为:1;75.
16.如图所示,ABC为一玻璃棱镜的截面,该截面是由半径为R的圆弧的一部分和一直角三角形组成的,O点为圆心,R=20cm,∠AOB=60°,折射率n=2,一束平行光垂直于AB面射入玻璃棱镜。求:
(1)光线由该棱镜材料射向空气时发生全反射的临界角;
(2)BC面上有光线逸出部分的弧长。
【解答】解:(1)折射率n=2,根据临界角公式 sinC=得光线由该棱镜材料射向空气时发生全反射的临界角C=30°;
(2)当入射点在临界点以上时,入射角大于临界角,光线发生全反射,不能BC面射出,当入射点在临界点下时,光线能穿出BC面.
根据几何知识 在BC弧面上有光线射出的部分弧长为S=R =.
答:(1)光线由该棱镜材料射向空气时发生全反射的临界角是30°;
(2)BC面上有光线逸出部分的弧长是。
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)2020年3月20日,电影《放射性物质》在伦敦首映,该片的主角﹣﹣居里夫人是放射性元素钋(Po)的发现者。钋210的半衰期是138天;钋210核发生衰变时,会产生α粒子和原子核X,并放出γ射线。下列说法正确的是( )
A.γ射线是高速电子流
B.原子核X的中子数为82
C.10个钋210核经过138天,一定还剩下5个钋核
D.衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量
2.(6分)某短跑运动员完成100m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1:4,则该运动员在加速阶段的加速度为( )
A.2.0m/s2 B.2.5m/s2 C.3.0m/s2 D.3.5m/s2
3.(6分)满载A国公民的一航班在飞行途中神秘消失,A国推断航班遭到敌对国家劫持,政府立即调动大量海空军事力量进行搜救,并在第一时间紧急调动了21颗卫星参与搜寻,“调动”卫星的措施之一就是减小卫星环绕地球运动的轨道半径,降低卫星运行的高度,以有利于发现地面(或海洋)目标,下面说法正确的是( )
A.轨道半径减小后,卫星的环绕重力势能增大
B.轨道半径减小后,卫星的环绕速度增大
C.轨道半径减小后,卫星的环绕机械能增大
D.轨道半径减小后,卫星的环绕周期增大
4.(6分)如图所示,在高度不同的两水平台阶上放有质量分别为m1、m2的两物体A、B,物体间用轻弹簧相连,弹簧与竖直方向夹角为θ.在物体A左端施加水平拉力F,使A、B均处于静止状态,已知物体A表面光滑,重力加速度为g,则下列说法正确的是( )
A.弹簧弹力的大小为
B.m1与m2一定相等
C.地面对B的支持力可能为零
D.地面对B的摩擦力大小为F
5.(6分)如图所示,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧轨道,BC段是长为L的粗糙水平轨道,两段轨道相切于B点。一质量为m、可视为质点的滑块从小车上的A点由静止开始沿轨道下滑,然后滑入BC轨道,最后恰好停在C点。已知小车质量M=4m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g,则( )
A.全过程滑块在水平方向上相对地面的位移的大小为R+L
B.小车在运动过程中速度的最大值为
C.全过程小车相对地面的位移大小为
D.μ、L、R三者之间的关系为R=μL
6.(6分)利用霍尔元件可以进行微小位移的测量,而半导体是制作霍尔元件的重要材料,若其中的载流子带正电,则成为P型半导体,若其中的载流子带负电,则称为N型半导体。如图甲所示,将固定有一个带有由P型半导体制成的霍尔元件的物体置于两块磁性强弱相同、同极相对放置的磁体缝隙中,建立如图乙所示的空间坐标系。保持沿x方向通过霍尔元件的电流I不变,当物体沿z轴方向移动时,由于不同位置处磁感应强度B不同,霍尔元件将在y轴方向的上、下表面间产生不同的霍尔电压UH。当用霍尔元件处于中间位置时,磁感应强度B为0,UH为0,将该点作为位移的零点。现将一个电压表并联在霍尔元件的两端,当霍尔元件的位置坐标为z=z0>0时,电压表的示数U=U0>0。已知在小范围内,磁感应强度B的大小和坐标z成正比,这样就可以把电压表当成测量物体微小位移的仪表。下列说法中正确的是( )
A.保持其他条件不变,仅换用由N型半导体制成的霍尔元件,则有z=z0时,U=﹣U0
B.保持其他条件不变,仅将两磁体的放置方向变为两S极,则有z=z0时,U=﹣U0
C.保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,U=U0
D.保持其他条件不变,仅减小霍尔元件沿y轴方向的厚度,则可以提高测量的精确度
7.(6分)如图,边界OM与ON间有垂直纸面向里的匀强磁场磁感应强度为B。边界ON上有一粒子源S,沿平行于纸面向磁场内各个方向发射大量带电荷量为+q、质量为m的相同速率的同种粒子,其中部分粒子能从边界OM射出磁场。已知∠MON=30°,OS=d,且从OM射出的粒子在磁场中运动的最短时间为。不考虑粒子间的相互作用,则( )
A.粒子的速率为
B.粒子的速率为
C.从OM射出的粒子,射出时与O点的最远距离为2d
D.从OM射出的粒子,射出时与O点的最远距离为d
8.(6分)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑。现将一质量为m、带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
A.小球释放后,到达最低点D时速度最大
B.小球释放后,到达B点时速度为零,并在BDA间往复运动
C.小球第一次经过最低点D和最高点C时对管壁的压力大小之比为5:1
D.小球第一次和第二次经过最高点C时对管壁的压力大小之比为1:3且方向相同
二.实验题(共4小题,满分47分)
9.(5分)(1)甲、乙、丙三个实验小组分别采用如图(甲)、(乙)、(丙)所示的实验装置,验证“当质量一定时,物体运动的加速度与它所受的合力成正比”这一物理规律。已知他们使用的小车完全相同,小车的质量为M,重物的质量为m,试回答下列问题:
①甲、乙、丙实验中,必须平衡小车和长木板之间的摩擦力的实验小组是 。
A.甲、乙、丙
B.甲、乙
C.甲、丙
②实验时,必须满足“M远大于m”的实验小组是 (填:甲、乙、丙)。
③实验时,甲、丙两组同学的操作均完全正确,他们作出的a﹣F图线如图(丁)中B、C所示,则甲、丙两组实验对应的图线依次是 。
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,以弹簧测力计的示数F为横坐标,加速度a为纵坐标,画出的a﹣F图线是如图(丁)中A为一条直线。测出图线与横坐标的夹角为θ;求得图线的斜率为k。则小车的质量为 。
A.
B.
C.
D.k
10.(10分)用伏安法测定一个待测电阻Rx的阻值(阻值约为150Ω),实验室提供如下器材:
电源E:电动势为2V,内阻不计;
电流表A1:量程0~15mA,内阻约为50Ω;
电流表A2:量程0~300μA,内阻为800Ω;
滑动变阻器R1:阻值范围0~10Ω,额定电流2A;
电阻箱R2:阻值范围0~9999Ω,额定电流1A;
开关S、导线若干。
要求实验中尽可能准确地测量Rx的阻值,请回答下列问题:
(1)为了测量待测电阻Rx两端的电压,可以将电流表 (填写器材代号)与电阻箱串联,并将电阻箱阻值调到 Ω,这样可以改装成一个量程为3.0V的电压表;
(2)请根据实物图2,结合所选器材在方框(图1)中画电路图,并标出所选器材的相应符号;
(3)调节滑动变阻器R1,两电流表的示数如图3所示,可读出电流表A1的示数为 mA,电流表A2的示数为 μA,测得待测电阻Rx的较准确值为 Ω(计算结果保留三位有效数字)。
11.(12分)如图所示,长为l的绝缘轻细线一端固定在O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O点正下方的O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。已知电场的范围足够大,空气阻力可忽略不计,重力加速度为g。
(1)求该匀强电场的电场强度大小;
(2)若在A点施加一个拉力,将小球从A点沿圆弧缓慢拉回到O′点,则所施拉力至少要做多少功;
(3)若将小球从O′点由静止释放,求在其运动到最高点的过程中,电场力所做的功W;
(4)若将小球从O′点由静止释放,求其运动到A点时的速度;
(5)若将小球从O′点由静止释放,求小球运动到A点时所受细线对它的拉力大小T;
(6)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求细线断开后小球运动的加速度;
(7)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求小球此后运动到最高点时的速度大小;
(8)若小球在A点附近小角度(小于5°)往复运动,求它从A点出发后到第二次再通过A点的过程中所经历的时间。
12.(20分)如图所示,一倾角为θ的固定斜面底端安装一挡板,物块Q静止在与挡板相距为s(足够大)的A处。某时刻,物块P以沿斜面向下的速度v0与Q发生弹性碰撞,已知Q与斜面间的动摩擦因数为2tanθ,最大静摩擦力等于滑动摩擦力,P与斜面间无摩擦,两物块(视为质点)质量均为m,取重力加速度为g。
(1)求P与Q第一次碰撞后瞬间各自的速度大小;
(2)求P与Q第二次碰撞前瞬间各自的速度大小;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,求Q停止的位置与挡板的距离。
三.多选题(共2小题,满分15分)
13.(5分)如图所示,电路与一绝热密闭气缸相连,R为电阻丝,气缸内有一定质量的理想气体,外界大气压恒定。闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法正确的是( )
A.气体的内能增加
B.气体分子平均动能不变
C.气体的压强不变
D.气体分子对容器器壁碰撞的次数减小了
E.电热丝放出的热量等于气体对外所做的功
14.(10分)如图所示,两端开口内壁光滑的导热汽缸竖直固定放置,质量分别为m和2m的两个活塞A、B由长度为2L的轻杆相连,两活塞的横截面积分别为S和2S,活塞间封闭有一定质量的理想气体。开始时,活塞B距离较细汽缸底端为L,整个装置处于静止状态。此时大气压强为p0=,汽缸周围温度为127℃,现在活塞A上部缓慢倒入细沙,直到活塞A恰好位于较细气缸底部。重力加速度为g。
(1)求加入细沙的质量;
(2)保持细沙质量不变,再缓慢降低气体温度,使活塞回到原来位置,内能减少了△U,求此时封闭气体的温度及此过程中气体放出的热量。
四.填空题(共2小题)
15.一列简谐横波沿x轴传播,t=0时刻波刚传到x=2.5m处,其波形如图甲所示。P、Q为介质中两个质点,其平衡位置xp=0.5m,xQ=5m,图乙是质点P的振动图像。则该简谐横波的波速为 m/s;10s内Q质点通过的路程为 cm。
16.如图所示,ABC为一玻璃棱镜的截面,该截面是由半径为R的圆弧的一部分和一直角三角形组成的,O点为圆心,R=20cm,∠AOB=60°,折射率n=2,一束平行光垂直于AB面射入玻璃棱镜。求:
(1)光线由该棱镜材料射向空气时发生全反射的临界角;
(2)BC面上有光线逸出部分的弧长。
2021-2022学年安徽省芜湖市高三(上)期末物理模拟试卷(1)
参考答案与试题解析
一.选择题(共8小题,满分48分,每小题6分)
1.(6分)2020年3月20日,电影《放射性物质》在伦敦首映,该片的主角﹣﹣居里夫人是放射性元素钋(Po)的发现者。钋210的半衰期是138天;钋210核发生衰变时,会产生α粒子和原子核X,并放出γ射线。下列说法正确的是( )
A.γ射线是高速电子流
B.原子核X的中子数为82
C.10个钋210核经过138天,一定还剩下5个钋核
D.衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量
【解答】解:A、γ射线的实质是频率很高的电磁波,不是电子流,故A错误;
B、根据发生核反应时,质量数与电荷数守恒,可得原子核X的质子数为:84﹣2=82,质量数为:210﹣4=206,依据质量数等于质子数与中子数之和,得原子核X的中子数为206﹣82=124,故B错误;
C、半衰期是大量放射性元素的原子核中有一半发生衰变的时间,对个别的放射性原子核没有意义,故C错误;
D、由于衰变的过程中释放能量,根据质能方程可知存在质量亏损,所以衰变后产生的α粒子与原子核X的质量之和小于衰变前钋210核的质量,故D正确。
故选:D。
2.(6分)某短跑运动员完成100m赛跑的过程可简化为匀加速直线运动和匀速直线运动两个阶段。一次比赛中,该运动员用12s跑完全程,已知该运动员在加速阶段的位移和匀速阶段的位移之比为1:4,则该运动员在加速阶段的加速度为( )
A.2.0m/s2 B.2.5m/s2 C.3.0m/s2 D.3.5m/s2
【解答】解:设运动员加速时间为t1,匀速时间为t2,匀速运动的速度为v,
加速的位移为:x1=t1
匀速的位移:x2=vt2
x1+x2=100m
x1:x2=1:4
解得:t1=4s,t2=8s,
x1=20m,x2=80m,
匀加速阶段,根据位移时间公式:
x1=
解得:a=2.5m/s2
故B正确;ACD错误。
故选:B。
3.(6分)满载A国公民的一航班在飞行途中神秘消失,A国推断航班遭到敌对国家劫持,政府立即调动大量海空军事力量进行搜救,并在第一时间紧急调动了21颗卫星参与搜寻,“调动”卫星的措施之一就是减小卫星环绕地球运动的轨道半径,降低卫星运行的高度,以有利于发现地面(或海洋)目标,下面说法正确的是( )
A.轨道半径减小后,卫星的环绕重力势能增大
B.轨道半径减小后,卫星的环绕速度增大
C.轨道半径减小后,卫星的环绕机械能增大
D.轨道半径减小后,卫星的环绕周期增大
【解答】解:A、卫星轨道半径减小,卫星离地面高度降低,卫星的重力势能减小,故A错误;
B、据可知,卫星的线速度v=,可知当轨道半径减小后,卫星的环绕速度v增大,故B正确;
C、卫星减小轨道半径时,需要减速做近心运动,在同一位置减速时,势能不变动能减小,卫星的机械能减小,故轨道半径减小后,卫星的环绕机械能减小,故C错误;
D、据可知,卫星的环绕周期T=,卫星轨道半径减小后,卫星的环绕周期减小,故D错误。
故选:B。
4.(6分)如图所示,在高度不同的两水平台阶上放有质量分别为m1、m2的两物体A、B,物体间用轻弹簧相连,弹簧与竖直方向夹角为θ.在物体A左端施加水平拉力F,使A、B均处于静止状态,已知物体A表面光滑,重力加速度为g,则下列说法正确的是( )
A.弹簧弹力的大小为
B.m1与m2一定相等
C.地面对B的支持力可能为零
D.地面对B的摩擦力大小为F
【解答】解:D、对整体受力分析可知,整体受重力、支持力、拉力;要使整体处于平衡,则水平方向一定有向右的摩擦力作用在m2上,且大小与F相同;故D正确;
C、因m2与地面间有摩擦力;则一定有支持力;故C错误;
A、再对m2受力分析可知,弹力水平方向的分力应等于F,故弹力T=,故A错误;
B、因竖直方向上的受力不明确,无法确定两物体的质量关系;也无法求出弹簧弹力与重力的关系;故B错误;
故选:D。
5.(6分)如图所示,质量为M的小车静止在光滑水平面上,小车AB段是半径为R的四分之一圆弧轨道,BC段是长为L的粗糙水平轨道,两段轨道相切于B点。一质量为m、可视为质点的滑块从小车上的A点由静止开始沿轨道下滑,然后滑入BC轨道,最后恰好停在C点。已知小车质量M=4m,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g,则( )
A.全过程滑块在水平方向上相对地面的位移的大小为R+L
B.小车在运动过程中速度的最大值为
C.全过程小车相对地面的位移大小为
D.μ、L、R三者之间的关系为R=μL
【解答】解:AC、设全过程滑块相对地面的位移大小为x,则小车相对地面位移大小为s=R+L﹣x,
滑块与小车组成的系统在水平方向动量守恒,以向右为正方向,在水平方向,由动量守恒定律得:
mv滑块﹣Mv小车=0,则m﹣M=0,由题意可知:M=4m,解得:x=,s=,故A错误,C正确;
B、滑块到达B点时小车速度最大,滑块在圆弧轨道下滑过程系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得:
mv滑块﹣Mv小车=0
由机械能守恒定律得:mgR=
解得:v小车=,故B正确;
D、滑块恰好停在C点,由能量守恒定律得:mgR=μmgL,解得:R=μL,故D正确。
故选:BCD。
6.(6分)利用霍尔元件可以进行微小位移的测量,而半导体是制作霍尔元件的重要材料,若其中的载流子带正电,则成为P型半导体,若其中的载流子带负电,则称为N型半导体。如图甲所示,将固定有一个带有由P型半导体制成的霍尔元件的物体置于两块磁性强弱相同、同极相对放置的磁体缝隙中,建立如图乙所示的空间坐标系。保持沿x方向通过霍尔元件的电流I不变,当物体沿z轴方向移动时,由于不同位置处磁感应强度B不同,霍尔元件将在y轴方向的上、下表面间产生不同的霍尔电压UH。当用霍尔元件处于中间位置时,磁感应强度B为0,UH为0,将该点作为位移的零点。现将一个电压表并联在霍尔元件的两端,当霍尔元件的位置坐标为z=z0>0时,电压表的示数U=U0>0。已知在小范围内,磁感应强度B的大小和坐标z成正比,这样就可以把电压表当成测量物体微小位移的仪表。下列说法中正确的是( )
A.保持其他条件不变,仅换用由N型半导体制成的霍尔元件,则有z=z0时,U=﹣U0
B.保持其他条件不变,仅将两磁体的放置方向变为两S极,则有z=z0时,U=﹣U0
C.保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,U=U0
D.保持其他条件不变,仅减小霍尔元件沿y轴方向的厚度,则可以提高测量的精确度
【解答】解:P型半导体在z=z0>0区域,磁场方向向左,电流沿x方向,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,P型半导体载流子带正电,故上表面电势高,因测的U=U0>0,故半导体上表面接电压表正极。
A、保持其他条件不变,换用由N型半导体制成的霍尔元件,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,N型半导体载流子带负电,故上表面电势低,因半导体上表面接电压表正极,故电压表示数为﹣U0,故A正确;
B、保持其他条件不变,仅将两磁体的放置方向变为两S极,磁场方向变为向右,应用左手定则可判断出载流子向y轴负方向移动,即向半导体下表面移动,P型半导体载流子带正电,故下表面电势高,因半导体上表面接电压表正极,故电压表示数为﹣U0,故B正确;
C、保持其他条件不变,仅将电流I的方向变为沿﹣x方向,则有z=﹣z0时,磁场方向变为向右,应用左手定则可判断出载流子向y轴正方向移动,即向半导体上表面移动,P型半导体载流子带正电,故上表面电势高,因半导体上表面接电压表正极,故电压表示数为U0,故C正确;
D、设y轴方向的厚度为d,沿z轴方向的厚度为b,达到稳定后有,又I=nqSv=nqbdv,联立得:U=,即U与d无关系,故D错误;
故选:ABC。
7.(6分)如图,边界OM与ON间有垂直纸面向里的匀强磁场磁感应强度为B。边界ON上有一粒子源S,沿平行于纸面向磁场内各个方向发射大量带电荷量为+q、质量为m的相同速率的同种粒子,其中部分粒子能从边界OM射出磁场。已知∠MON=30°,OS=d,且从OM射出的粒子在磁场中运动的最短时间为。不考虑粒子间的相互作用,则( )
A.粒子的速率为
B.粒子的速率为
C.从OM射出的粒子,射出时与O点的最远距离为2d
D.从OM射出的粒子,射出时与O点的最远距离为d
【解答】解:AB、粒子在磁场中运动做匀速圆周运动,入射点是S,出射点在OM直线上,出射点与S点的连线为轨迹的一条弦。当从边界OM射出的粒子在磁场中运动的时间最短时,轨迹的弦最短,即通过S点做OM的垂线SC为最短的弦,如图所示;
且
所以θ==120°,则弦切角为60°
由几何关系有:SC=2Rsin60° 而SC=d×sin30°
由洛伦兹力提供向心力可得qvB=m ,解得:R=
联立可得:v=,故A错误,B正确;
CD、若最远点为D点,当SD为轨迹圆的直径时D点离O最远,由几何关系知,△ODS是直角三角形,那么:SD==,故C错误,D正确。
故选:BD。
8.(6分)如图所示,半径为R的环形塑料管竖直放置,AB为该环的水平直径,且管的内径远小于环的半径,环的A、B及其以下部分处于水平向左的匀强电场中,管的内壁光滑。现将一质量为m、带电荷量为+q的小球从管中A点由静止释放,已知qE=mg,以下说法正确的是( )
A.小球释放后,到达最低点D时速度最大
B.小球释放后,到达B点时速度为零,并在BDA间往复运动
C.小球第一次经过最低点D和最高点C时对管壁的压力大小之比为5:1
D.小球第一次和第二次经过最高点C时对管壁的压力大小之比为1:3且方向相同
【解答】解:A、如图所示合力与重力的夹角满足tanθ==1,即θ=45°,当小球重力和电场力的合力正好沿半径方向时,小球的速度最大,所以速度最大点在D点的左侧,故A错误;
B、只有重力和电场力做功,带电小球到达B点,重力势能不变,电势能减小,故有动能,其动能大小等于电场力做的功,为qE 2R=,故B错误;
C、第一次过D点时,
根据动能定理可知:mgR+qER=m,
由牛顿第二定律可知:N1D﹣mg=m,
又由于qE=mg
故解得N1D=5mg
第一次过C点,
由牛顿第二定律可知:N1C+mg=m,
根据动能定理可知:2EqR﹣mgR=m,
又由于qE=mg
故解得N1C=mg,故C正确;
D、从A点释放到第二次到C点过程,
根据动能定理可知:﹣mgR+2qE 2R=mv2C2
在C点牛顿第二定律可知:N2C+mg=m
解得N2C=5mg,
故:N1C:N2C=1:5,故D错误;
故选:C。
二.实验题(共4小题,满分47分)
9.(5分)(1)甲、乙、丙三个实验小组分别采用如图(甲)、(乙)、(丙)所示的实验装置,验证“当质量一定时,物体运动的加速度与它所受的合力成正比”这一物理规律。已知他们使用的小车完全相同,小车的质量为M,重物的质量为m,试回答下列问题:
①甲、乙、丙实验中,必须平衡小车和长木板之间的摩擦力的实验小组是 A 。
A.甲、乙、丙
B.甲、乙
C.甲、丙
②实验时,必须满足“M远大于m”的实验小组是 甲 (填:甲、乙、丙)。
③实验时,甲、丙两组同学的操作均完全正确,他们作出的a﹣F图线如图(丁)中B、C所示,则甲、丙两组实验对应的图线依次是 CB 。
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,以弹簧测力计的示数F为横坐标,加速度a为纵坐标,画出的a﹣F图线是如图(丁)中A为一条直线。测出图线与横坐标的夹角为θ;求得图线的斜率为k。则小车的质量为 C 。
A.
B.
C.
D.k
【解答】解:(1)①(甲)、(乙)、(丙)三个图小车与长木板之间都有摩擦力,为保证小车受到的拉力就是所受的合力,所以都需要平衡摩擦力,故A正确,BC错误;
故选:A
②(乙)、(丙)两图绳上的力由弹簧测力计和力传感器直接读出,不需要用重物的重力代替,所以不需满足M m;(甲)图用重物的重力代替绳的拉力,必须满足M m;
③(甲)图用重物的重力代替绳子的拉力,需满足M m,随着m的增大,不满足M m时,图象出现弯曲,所以甲组对应的是C;(乙)、(丙)图根据拉力相等时,加速度a乙>a丙,从而判断乙组对应A,丙组对应B。故答案为:CB;
(2)小明同学采用(乙)图实验装置探究质量一定时加速度与力的关系的实验时,对小车由牛顿第二定律得:2F=Ma
以弹簧测力计的示数F为横坐标,加速度a为纵坐标,整理得:a=F,根据图线的斜率为k=,解得小车的质量为:M=,故C正确,ABD错误,
故选:C。
故答案为:(1)①A、②甲、③CB;(2)C
10.(10分)用伏安法测定一个待测电阻Rx的阻值(阻值约为150Ω),实验室提供如下器材:
电源E:电动势为2V,内阻不计;
电流表A1:量程0~15mA,内阻约为50Ω;
电流表A2:量程0~300μA,内阻为800Ω;
滑动变阻器R1:阻值范围0~10Ω,额定电流2A;
电阻箱R2:阻值范围0~9999Ω,额定电流1A;
开关S、导线若干。
要求实验中尽可能准确地测量Rx的阻值,请回答下列问题:
(1)为了测量待测电阻Rx两端的电压,可以将电流表 A2 (填写器材代号)与电阻箱串联,并将电阻箱阻值调到 9200 Ω,这样可以改装成一个量程为3.0V的电压表;
(2)请根据实物图2,结合所选器材在方框(图1)中画电路图,并标出所选器材的相应符号;
(3)调节滑动变阻器R1,两电流表的示数如图3所示,可读出电流表A1的示数为 12.5 mA,电流表A2的示数为 180 μA,测得待测电阻Rx的较准确值为 146 Ω(计算结果保留三位有效数字)。
【解答】解:(1)由于题目没有给电压表,为测电压可以将已知内阻的电流表A2与电阻箱串联改装成电压表测电压,
由欧姆定律可知,把电流表改装成U=3.0V的电压表串联电阻阻值R===9200Ω;
(2)根据图示实物电路图作出实验电路图,实验电路图如图所示:
(3)电流表A1的量程是15mA,分度值是0.5mA,示数I1=12.5mA,
电流表A2的量程是300μA,分度值是10μA,而I2=180μA,
由欧姆定律可知,待测电阻阻值:Rx==Ω=146Ω。
故答案为:(1)A2;9200;(2)电路图如图所示;(3)12.5;180;146。
11.(12分)如图所示,长为l的绝缘轻细线一端固定在O点,另一端系一质量为m、带电荷+q的小球,小球静止时处于O点正下方的O′点。现将此装置放在水平向右的匀强电场中,小球静止在A点时细线与竖直方向成θ角。已知电场的范围足够大,空气阻力可忽略不计,重力加速度为g。
(1)求该匀强电场的电场强度大小;
(2)若在A点施加一个拉力,将小球从A点沿圆弧缓慢拉回到O′点,则所施拉力至少要做多少功;
(3)若将小球从O′点由静止释放,求在其运动到最高点的过程中,电场力所做的功W;
(4)若将小球从O′点由静止释放,求其运动到A点时的速度;
(5)若将小球从O′点由静止释放,求小球运动到A点时所受细线对它的拉力大小T;
(6)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求细线断开后小球运动的加速度;
(7)若将带电小球从O′点由静止释放,其运动到A点时细线断开,求小球此后运动到最高点时的速度大小;
(8)若小球在A点附近小角度(小于5°)往复运动,求它从A点出发后到第二次再通过A点的过程中所经历的时间。
【解答】解:(1)对带电小球受力分析如图所示,可得:tanθ=,解得:E=
(2)根据动能定理可知:WF+mgl(1﹣cosθ)﹣qElsinθ=0,解得:WF=
(3)根据对称性可知,小球摆到最高点时摆线与竖直方向夹角为2θ,则电场力做功为:W=Eqlsin2θ=mgtanθ lsin2θ=2mglsin2θ
(4)从O′点到A点,动能定理:qElsinθ﹣mgl(1﹣cosθ)=,解得:,方向与水平方向成θ角斜向上
(5)在A点由牛顿第二定律:T﹣mgcosθ=,解得:T=mg()
(6)到A点时细绳断开,则此时小球受向下的重力和向右的电场力,其合力为:
由牛顿第二定律可知:a===,方向与竖直方向成θ角斜向下。
(7)运动到A点时细绳断开,小球此后在水平方向做匀加速运动,水平初速度为:vx0=vAcosθ,水平加速度为:ax=asinθ
竖直方向做匀减速运动,竖直初速度为:vy0=vAsinθ,竖直加速度为:ay=acosθ
运动到最高点所用的时间为:t==
则水平速度即为最高点的速度:vx=vx0+axt=vAcosθ+asinθ =
(8)若小球在A点附近小角度往复运动,则可看做单摆模型,周期T=,其等效重力加速度为:,那么周期化简得:T=
它从A点出发后到第二次再通过A点的过程中所经历的时间为一个周期,则时间t=T=
答:(1)匀强电场的电场强度大小为:;
(2)拉力至少要做的功为:;
(3)电场力做功W=2mglsin2θ;
(4)运动到A点速度大小为,方向与水平方向成θ角斜向上;
(5)小球运动到A点所受细绳对它的拉力T=;
(6)细绳断开后小球运动的加速度大小为,方向与竖直方向成θ角斜向下;
(7)小球运动到最高点时的速度大小为;
(8)小球从A点出发后到第二次再通过A点的过程中所经历的时间为。
12.(20分)如图所示,一倾角为θ的固定斜面底端安装一挡板,物块Q静止在与挡板相距为s(足够大)的A处。某时刻,物块P以沿斜面向下的速度v0与Q发生弹性碰撞,已知Q与斜面间的动摩擦因数为2tanθ,最大静摩擦力等于滑动摩擦力,P与斜面间无摩擦,两物块(视为质点)质量均为m,取重力加速度为g。
(1)求P与Q第一次碰撞后瞬间各自的速度大小;
(2)求P与Q第二次碰撞前瞬间各自的速度大小;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,求Q停止的位置与挡板的距离。
【解答】解:(1)PQ组成的系统,在第一次碰撞过程中,沿斜面方向根据动量守恒可得:mv0=mvP1+mvQ1
在第一次碰撞过程中,PQ组成的系统,根据能量守恒可得:
联立解得:vp1=0,vQ1=v0
(2)对Q受力分析可知:μmgcosθ﹣mgsinθ=maQ
解得aQ=gsinθ
Q匀减速运动,则
度P受力分析可知mgsinθ=maP,解得aP=gsinθ
P匀加速直线运动,
碰撞条件为xP=xQ,
解得t=
v′P=aPtv′Q=v0﹣aQt
解得:v′P=v0,v′Q=0
(3)任意两次碰撞位置的距离L=
PQ最后一次碰撞的位置与挡板距离x=s﹣nL
其中n为结果的整数部分
PQ最后一次碰撞后,Q运动至挡板出由
于是Q与挡板碰撞前速度
Q与挡板碰撞前后有:
Q反弹的速度
Q沿斜面上升过程
于是:Q停下位置距挡板△x=,其中n为的整数部分
答:(1)P与Q第一次碰撞后瞬间各自的速度大小分别为0和v0;
(2)求P与Q第二次碰撞前瞬间各自的速度大小分别为v0和0;
(3)当Q与挡板发生碰撞瞬间,撤去物块P,且Q与挡板碰撞时损失的能量是碰前的,Q停止的位置与挡板的距离,其中n为的整数部分
三.多选题(共2小题,满分15分)
13.(5分)如图所示,电路与一绝热密闭气缸相连,R为电阻丝,气缸内有一定质量的理想气体,外界大气压恒定。闭合电键后,绝热活塞K缓慢且无摩擦地向右移动,则下列说法正确的是( )
A.气体的内能增加
B.气体分子平均动能不变
C.气体的压强不变
D.气体分子对容器器壁碰撞的次数减小了
E.电热丝放出的热量等于气体对外所做的功
【解答】解:AB、闭合电键后,给气体加热,温度升高,分子平均动能增大,内能增大,故A正确,B错误。
C、以活塞为研究对象,根据平衡条件知,密闭气体的压强等于外界大气压强,所以密闭气体压强不变,故C正确。
D、根据气体压强的微观意义,气体压强和单位时间对器壁单位面积的碰撞次数、分子平均动能有关;现气体压强不变,分子平均动能增大,则气体分子单位时间对器壁单位面积的碰撞次数减小,故D正确。
E、内能增大,△U>0,体积增大,气体对外做功,W<0,根据热力学第一定律△U=Q+W,有Q>0,则Q>﹣W>0,即电热丝放出的热量大于气体对外所做的功,故E错误。
故选:ACD。
14.(10分)如图所示,两端开口内壁光滑的导热汽缸竖直固定放置,质量分别为m和2m的两个活塞A、B由长度为2L的轻杆相连,两活塞的横截面积分别为S和2S,活塞间封闭有一定质量的理想气体。开始时,活塞B距离较细汽缸底端为L,整个装置处于静止状态。此时大气压强为p0=,汽缸周围温度为127℃,现在活塞A上部缓慢倒入细沙,直到活塞A恰好位于较细气缸底部。重力加速度为g。
(1)求加入细沙的质量;
(2)保持细沙质量不变,再缓慢降低气体温度,使活塞回到原来位置,内能减少了△U,求此时封闭气体的温度及此过程中气体放出的热量。
【解答】解:(1)设初始状态封闭气体的压强为p1,
对活塞整体,由平衡条件可得:p0S+p1×2S+3mg=p0×2S+p1S
设活塞A到达气缸底部时封闭气体的压强为p2、加入细沙的质量为m0,
对活塞与细沙整体,由平衡条件得:p0S+p2×2S+3mg+m0g=p0×2S+p2S
根据玻意耳定律得:p1(LS+2LS)=p2×2L×2S
解得:m0=0.5m
(2)降低温度过程中气体做等压变化,
由盖﹣吕萨克定律得:
代入数据解得:T2=300K
体积恢复过程中外界对气体做的功:W=p2LS
解得:W=1.5mgL
由热力学第一定律得:﹣△U=W﹣Q
解得:Q=1.5mgL+△U
答:(1)加入细沙的质量是0.5m;
(2)此时封闭气体的温度是300K,此过程中气体放出的热量是1.5mgL+△U。
四.填空题(共2小题)
15.一列简谐横波沿x轴传播,t=0时刻波刚传到x=2.5m处,其波形如图甲所示。P、Q为介质中两个质点,其平衡位置xp=0.5m,xQ=5m,图乙是质点P的振动图像。则该简谐横波的波速为 1 m/s;10s内Q质点通过的路程为 75 cm。
【解答】解:根据甲图知波长为:λ=2m,根据乙图知周期为:T=2s
所以波速为:=;
机械波传到Q点需要的时间为:
所以Q点振动的时间为:t2=10s﹣2.5s=7.5s
10s内Q质点通过的路程为:
从图中可以读出振幅为:A=5cm
所以:s=15A=15×5cm=75cm.
故答案为:1;75.
16.如图所示,ABC为一玻璃棱镜的截面,该截面是由半径为R的圆弧的一部分和一直角三角形组成的,O点为圆心,R=20cm,∠AOB=60°,折射率n=2,一束平行光垂直于AB面射入玻璃棱镜。求:
(1)光线由该棱镜材料射向空气时发生全反射的临界角;
(2)BC面上有光线逸出部分的弧长。
【解答】解:(1)折射率n=2,根据临界角公式 sinC=得光线由该棱镜材料射向空气时发生全反射的临界角C=30°;
(2)当入射点在临界点以上时,入射角大于临界角,光线发生全反射,不能BC面射出,当入射点在临界点下时,光线能穿出BC面.
根据几何知识 在BC弧面上有光线射出的部分弧长为S=R =.
答:(1)光线由该棱镜材料射向空气时发生全反射的临界角是30°;
(2)BC面上有光线逸出部分的弧长是。
同课章节目录
