华东师大版数学九年级上册 24.3.1 锐角三角函数 课件 (共16张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 24.3.1 锐角三角函数 课件 (共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 870.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 11:10:24 | ||
图片预览




文档简介
(共16张PPT)
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。
1米
10米
你想知道小明怎样算出的吗?
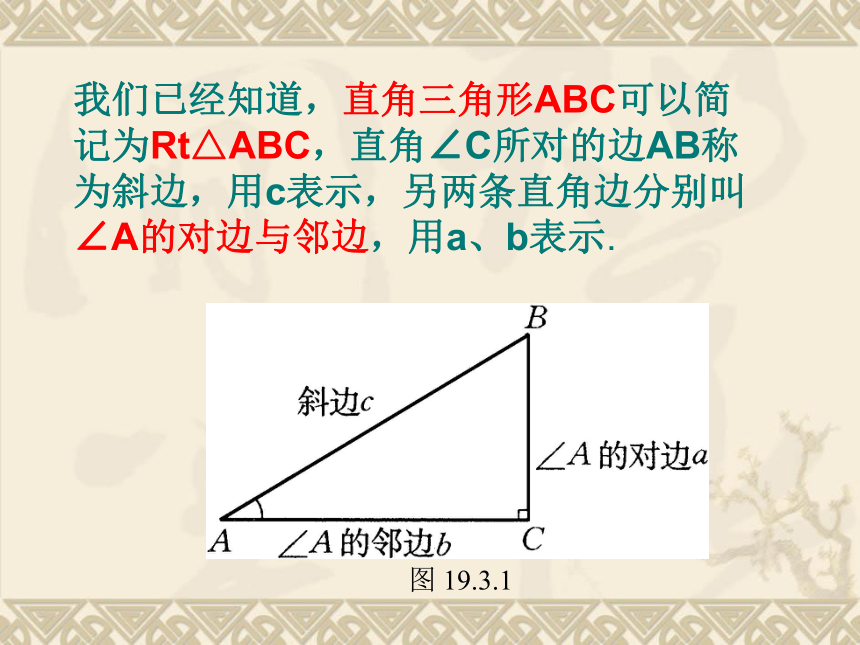
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
如图,在Rt△MNP中,∠N=90゜
∠P的对边是____,∠P的邻边是______;
∠M的对边是____,∠M的邻边是____;
MN
PN
PN
MN
想一想:∠P的对边、邻边与∠M的对边、邻边有什么关系?
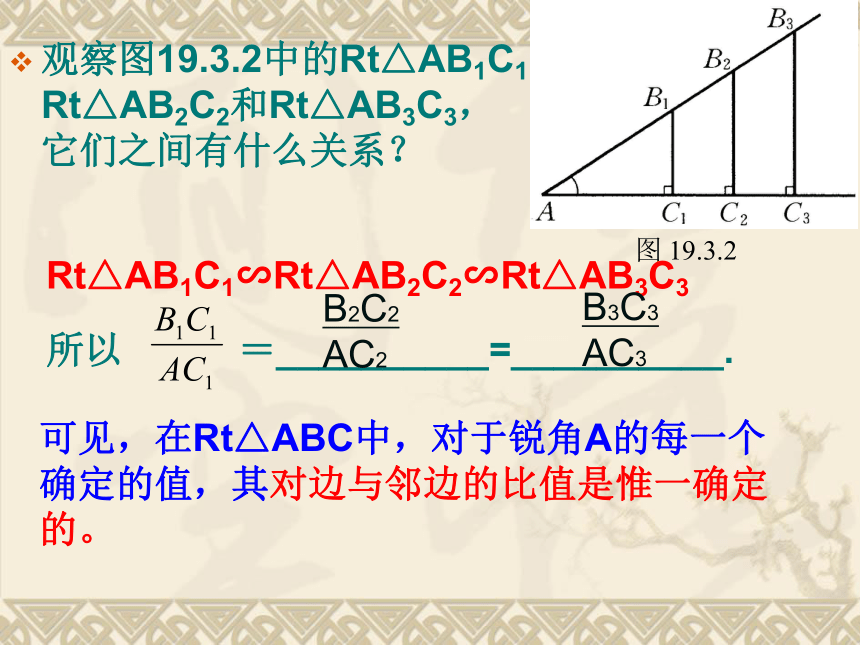
观察图19.3.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的。
B2C2
AC2
B3C3
AC3
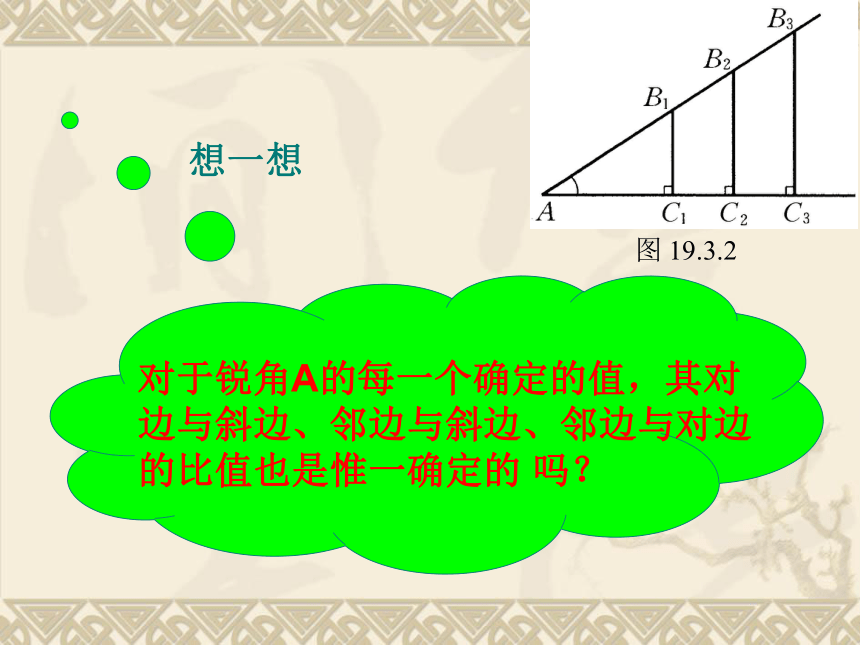
想一想
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的 吗?
这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A、cot A,即
sin A=
cos A=
tan A=
cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数。
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位
由感性知识上升到理性知识:
在Rt△ABC中,sinA和cosB有什么关系 tanA和cotB有什么关系
互余两角之间的三角函数关系
直角三角形两锐角互余:∠A+∠B=900
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
sinA=cosB或cosA=sinB.
tanA=cotB或cotA=tanB.
一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正 弦);
互余两角之间的三角函数关系
结合图形,将sinA=cosB或cosA=sinB. tanA=cotB或cotA=tanB.分别用文字语言叙述出来:
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
一个锐角的正切,等于它的余角的余切(或一个锐角的余切等于它的余角的正切);
一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正弦);
互余两角之间的三角函数关系
一般地,∠α的余角为900-∠α,即∠α和900-∠α角互为余角
回顾与思考
1
驶向胜利的彼岸
一个锐角的正切,等于它的余角的余切(或一个锐角的余切等于它的余角的正切);
理解定义:
1、你认为∠A的正弦、余弦的定义有什么区别?正切、余切呢?
2、你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?
0<sin A<1,0<cos A<1
3、
tan A与cot A之间有什么关系?
tan A cot A=1
4. sin A与cos A之间有什么关系?
练一练
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
练习:
1、下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。
A
B
C
D
2、1题中如果CD=5,AC=10,则sin∠ACD=
sin ∠DCB=
例3、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。
中考连接:
(1)在△ABC中,∠B=90 ,BC=3,AC=4,则tanA= cosA=
(2)tanA·cot20 =1,则锐角∠A=
小结
通过我们这一节课的探索与学习,你一定有好多的收获,你能把这些知识点加以收集与总结吗?
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1米.然后他很快就算出旗杆的高度了。
1米
10米
你想知道小明怎样算出的吗?
我们已经知道,直角三角形ABC可以简记为Rt△ABC,直角∠C所对的边AB称为斜边,用c表示,另两条直角边分别叫∠A的对边与邻边,用a、b表示.
如图,在Rt△MNP中,∠N=90゜
∠P的对边是____,∠P的邻边是______;
∠M的对边是____,∠M的邻边是____;
MN
PN
PN
MN
想一想:∠P的对边、邻边与∠M的对边、邻边有什么关系?
观察图19.3.2中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,它们之间有什么关系?
Rt△AB1C1∽Rt△AB2C2∽Rt△AB3C3
所以 =__________=__________.
可见,在Rt△ABC中,对于锐角A的每一个确定的值,其对边与邻边的比值是惟一确定的。
B2C2
AC2
B3C3
AC3
想一想
对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的 吗?
这几个比值都是锐角∠A的函数,记作sin A、cos A、tan A、cot A,即
sin A=
cos A=
tan A=
cot A=
分别叫做锐角∠A的正弦、余弦、正切、余切,统称为锐角∠A的三角函数。
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、 sinA 是一个比值 4、sinA 没有单位
由感性知识上升到理性知识:
在Rt△ABC中,sinA和cosB有什么关系 tanA和cotB有什么关系
互余两角之间的三角函数关系
直角三角形两锐角互余:∠A+∠B=900
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
sinA=cosB或cosA=sinB.
tanA=cotB或cotA=tanB.
一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正 弦);
互余两角之间的三角函数关系
结合图形,将sinA=cosB或cosA=sinB. tanA=cotB或cotA=tanB.分别用文字语言叙述出来:
回顾与思考
1
驶向胜利的彼岸
b
A
B
C
a
┌
c
一个锐角的正切,等于它的余角的余切(或一个锐角的余切等于它的余角的正切);
一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正弦);
互余两角之间的三角函数关系
一般地,∠α的余角为900-∠α,即∠α和900-∠α角互为余角
回顾与思考
1
驶向胜利的彼岸
一个锐角的正切,等于它的余角的余切(或一个锐角的余切等于它的余角的正切);
理解定义:
1、你认为∠A的正弦、余弦的定义有什么区别?正切、余切呢?
2、你能利用直角三角形的三边关系得到sinA与 cosA的取值范围吗?
0<sin A<1,0<cos A<1
3、
tan A与cot A之间有什么关系?
tan A cot A=1
4. sin A与cos A之间有什么关系?
练一练
1.判断对错:
A
10m
6m
B
C
1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√
√
×
×
sinA是一个比值(注意比的顺序),无单位;
2)如图,sinA= ( )
×
练习:
1、下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。
A
B
C
D
2、1题中如果CD=5,AC=10,则sin∠ACD=
sin ∠DCB=
例3、如图,在△ABC中, AB=BC=5,sinA=4/5,求△ABC 的面积。
中考连接:
(1)在△ABC中,∠B=90 ,BC=3,AC=4,则tanA= cosA=
(2)tanA·cot20 =1,则锐角∠A=
小结
通过我们这一节课的探索与学习,你一定有好多的收获,你能把这些知识点加以收集与总结吗?
