华东师大版数学九年级上册 23.3.3 相似三角形的性质 课件 (共33张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.3.3 相似三角形的性质 课件 (共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 419.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-07 11:12:56 | ||
图片预览










文档简介
(共33张PPT)
相似三角形的性质
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平分线的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
1,相似三角形有何特征?
(对应边成比例,对应角相等)
2,识别三角形相似的主要方法有那些?
两个角对应相等的两个三角形相似。
两边对应成比例且夹角相等的两个三角形相似 。
三边对应成比例的两个三角形相似。
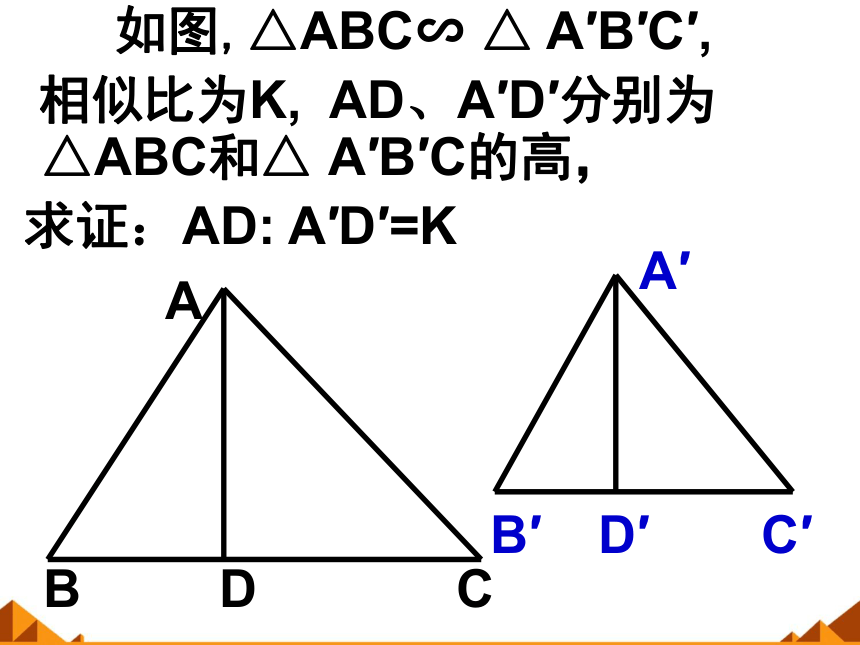
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的高,
求证:AD: A′D′=K
A
B
C
D
A′
B′
C′
D′
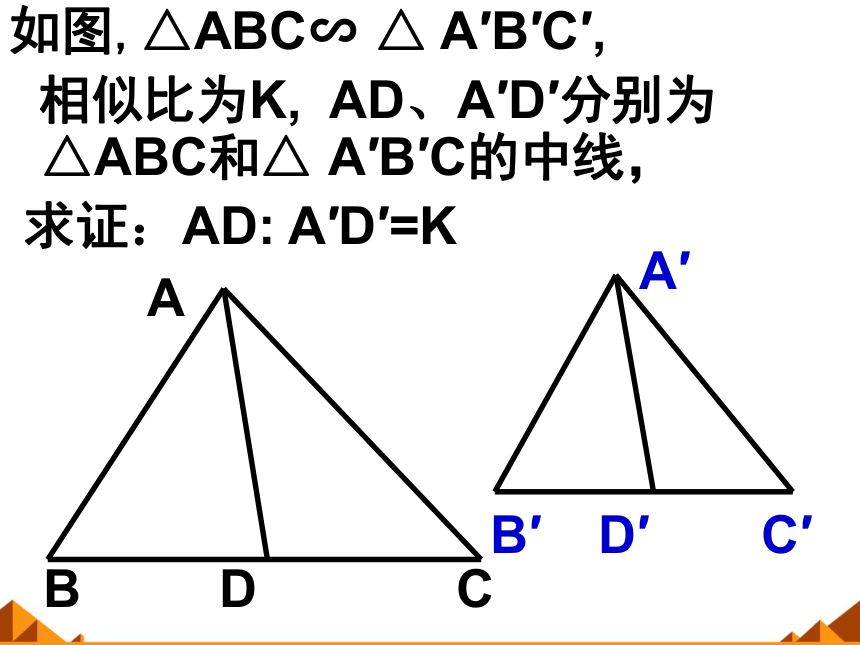
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的中线,
求证:AD: A′D′=K
C′
A
B
C
D
A′
B′
D′
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的角平分线,求证:AD: A′D′=K
A
B
C
D
B′
A′
C′
D′
如图,△ABC∽ △ A′B′C′,
相似比为K,AD、A′D′分别为 △ABC和△ A′B′C′的高,
求证:S△ABC :S△ A′B′C′的值
A
B
C
D
A′
B′
C′
D′
相似三角形性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
一,相似三角形的基本性质:
对应边成比例,对应角相等
二,相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
例1:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
?
C
B
A
例2:有同一块三角形土地的甲、乙两幅地图,比例尺分别为1:200和1:500,求甲地图与乙地图的相似比和面积比。
解
因为甲、乙两幅地图都与这块三角形土地相似,
所以这两幅地图相似。
设三角形土地的某一边长为m,
甲地图的对应边为a:200,乙地图的对应边为a:500,
所以这两幅地图相似比为
a
a
200
500
:
=
5
2
所以 它们的面积比为25:4
1,把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的 倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的 倍。
25
10
2,两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是————————。
100厘米、40厘米
50平方厘米、8平方厘米
如图,在 ABCD中,E是AB上一点,AC与DE相交于F,AE:EB=1:2,求 AEF与 CDF的相似比.若 AEF的面积为5平方厘米,求 CDF的面积。
B
F
E
D
C
A
练习:
如果把一个三角形按照下面的条件改成和它相似的三角形:
(1) 把边长扩大为原来的 100倍,那么面积扩大为原来的多少倍?
(2) 把面积扩大为原来的 100倍,那么边长扩大为原来的多少倍?
求三角形的三条中位线所围成的在角形与原三角形的面积的比.
如果把一个图形按 1 : 10 的比例缩小,那么缩小后的图形与原图形的面积比是多少?.
1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。
3∶5
3∶5
3∶5
9∶25
3∶5
2、把一个三角形扩大成和它相似的三角形,(1)如果把边长扩大为原来的10倍,那么面积扩大为原来的 倍。
(2)如果把面积扩大为原来的10倍,则边长应扩大为原来 的 倍。
100
3、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是 cm,面积 cm2。
14
如图,在△ABC中,AD:DB=1:2,DE∥BC,若△ABC的面积为9,
求S四边形DBCE
A
B
C
D
E
如图,在 ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,求S△EFB
D
A
B
C
E
F
如图,在 ABCD 中,AE:EB=1:2 ,若S△AEF=6cm2,求S△CDF
D
A
B
C
F
E
在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,若AB=10,BC=6,DE=2,求四边形DEBC的面积
A
B
C
D
E
∟
∟
5.如图,△ABC中,点D,E,F分别在边AB,AC,BC上,DF∥BC,EF∥AB , AF:FC=2 :3,S△ABC=S,
求平行四边形BEFD的面积。
A
D
E
F
B
C
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
M
P
B
N
Q
E
D
C
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
如图,△ABC中,BC=24㎝,高AD=12㎝,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H在AC、AB上,且EF:EH=4:3,求EF、EH的长
A
B
C
H
E
F
G
K
D
∟
如图,D、E是△ABC的边AB、AC上的点,且∠ADE= ∠C。
求证:AD·AB=AE·AC。
如图,D是△ABC的边BC上的点,且∠ADB= ∠BAC。
1、图中有相似的三角形吗?为什么?
2、求证:AB2=BC·BD。
1.如图在梯形ABCD中,AD∥BC, ∠A=90°,BD⊥ DC,试问(1)请你猜想图中有相似三角形吗?请写出来,并说明理由。
(2)如果CD= 3,BC= 5,你能求出哪些线段的长?
A
D
B
C
∟
∟
2.如图已知∠1=∠2,若再增加一个条
件能使结论AB·ED=AD·BC成立,则这
个条件可以是_________________。
2
1
A
C
E
B
D
分析:①从角的角度思考:∠D=∠B或∠AED=∠C
② 从边的角度思考:AD:AB=AE:AC
如图:在Rt△ABC中,有正方形DEFG,且E、F在斜边BC上,D、G分别在AB、AC上.试说明:EF2=BE·FC
G
F
E
D
C
B
A
解:
四边形DEFG是正方形
∠DEB=∠GFC=90°,
EF=DE=FG.
∵
∴
又∵ ∠B+∠C=90°,∠B+∠BDE=90°
∴
∠BDE=∠C
Rt△BED∽ Rt△GFC
∴
BE
DE
FC
GF
=
∴
BE
EF
FC
EF
=
∴
∴
EF2=BE·FC
F
E
D
C
B
A
如图:已知∠BAC=90°,BD=DC, DE⊥BC交AC于E,交BA的延长线于F.试说明:AD2=DE·DF
由AD2=DE·DF,得
故只要说明△ADE∽ △FDA即可
分析:
AD
DE
AD
DF
=
点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)
1.相似三角形对应高的比等于相似比。
2.相似三角形对应中线的比等于相似比。
3.相似三角形对应角平分线的比等于相似比。
相似三角形的性质:
4.相似三角形周长的比等于相似比。
5.相似三角形面积的比等于相似比的平方。
相似三角形的性质
学习目标
1.在理解相似三角形基本性质的基础上,掌握相似三角形对应中线、对应高线、对应角平分线的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
2.通过实践体会相似三角形的性质,会用性质解决相关的问题。
1,相似三角形有何特征?
(对应边成比例,对应角相等)
2,识别三角形相似的主要方法有那些?
两个角对应相等的两个三角形相似。
两边对应成比例且夹角相等的两个三角形相似 。
三边对应成比例的两个三角形相似。
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的高,
求证:AD: A′D′=K
A
B
C
D
A′
B′
C′
D′
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的中线,
求证:AD: A′D′=K
C′
A
B
C
D
A′
B′
D′
如图,△ABC∽ △ A′B′C′,
相似比为K, AD、A′D′分别为 △ABC和△ A′B′C的角平分线,求证:AD: A′D′=K
A
B
C
D
B′
A′
C′
D′
如图,△ABC∽ △ A′B′C′,
相似比为K,AD、A′D′分别为 △ABC和△ A′B′C′的高,
求证:S△ABC :S△ A′B′C′的值
A
B
C
D
A′
B′
C′
D′
相似三角形性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
一,相似三角形的基本性质:
对应边成比例,对应角相等
二,相似三角形的性质:
相似三角形对应高的比、对应中线的比、对应角平分线的比、周长的比等于相似比。
相似三角形面积的比等于相似比的平方。
例1:如图,△ABC~△A'B'C',它们的周长分别是60厘米和72厘米,且AB=15厘米,B'C'=24厘米。求:BC、AC、A'B'、A'C'。
C'
B'
A'
?
C
B
A
例2:有同一块三角形土地的甲、乙两幅地图,比例尺分别为1:200和1:500,求甲地图与乙地图的相似比和面积比。
解
因为甲、乙两幅地图都与这块三角形土地相似,
所以这两幅地图相似。
设三角形土地的某一边长为m,
甲地图的对应边为a:200,乙地图的对应边为a:500,
所以这两幅地图相似比为
a
a
200
500
:
=
5
2
所以 它们的面积比为25:4
1,把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的 倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的 倍。
25
10
2,两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是————————。
100厘米、40厘米
50平方厘米、8平方厘米
如图,在 ABCD中,E是AB上一点,AC与DE相交于F,AE:EB=1:2,求 AEF与 CDF的相似比.若 AEF的面积为5平方厘米,求 CDF的面积。
B
F
E
D
C
A
练习:
如果把一个三角形按照下面的条件改成和它相似的三角形:
(1) 把边长扩大为原来的 100倍,那么面积扩大为原来的多少倍?
(2) 把面积扩大为原来的 100倍,那么边长扩大为原来的多少倍?
求三角形的三条中位线所围成的在角形与原三角形的面积的比.
如果把一个图形按 1 : 10 的比例缩小,那么缩小后的图形与原图形的面积比是多少?.
1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。
3∶5
3∶5
3∶5
9∶25
3∶5
2、把一个三角形扩大成和它相似的三角形,(1)如果把边长扩大为原来的10倍,那么面积扩大为原来的 倍。
(2)如果把面积扩大为原来的10倍,则边长应扩大为原来 的 倍。
100
3、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是 cm,面积 cm2。
14
如图,在△ABC中,AD:DB=1:2,DE∥BC,若△ABC的面积为9,
求S四边形DBCE
A
B
C
D
E
如图,在 ABCD中,E为AB延长线上一点,AB:AE=2:5,若S△DFC=12cm2,求S△EFB
D
A
B
C
E
F
如图,在 ABCD 中,AE:EB=1:2 ,若S△AEF=6cm2,求S△CDF
D
A
B
C
F
E
在△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,若AB=10,BC=6,DE=2,求四边形DEBC的面积
A
B
C
D
E
∟
∟
5.如图,△ABC中,点D,E,F分别在边AB,AC,BC上,DF∥BC,EF∥AB , AF:FC=2 :3,S△ABC=S,
求平行四边形BEFD的面积。
A
D
E
F
B
C
如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
M
P
B
N
Q
E
D
C
A
解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以
AE
AD
=
PN
BC
如图,△ABC中,BC=24㎝,高AD=12㎝,矩形EFGH的两个顶点E、F在BC上,另两个顶点G、H在AC、AB上,且EF:EH=4:3,求EF、EH的长
A
B
C
H
E
F
G
K
D
∟
如图,D、E是△ABC的边AB、AC上的点,且∠ADE= ∠C。
求证:AD·AB=AE·AC。
如图,D是△ABC的边BC上的点,且∠ADB= ∠BAC。
1、图中有相似的三角形吗?为什么?
2、求证:AB2=BC·BD。
1.如图在梯形ABCD中,AD∥BC, ∠A=90°,BD⊥ DC,试问(1)请你猜想图中有相似三角形吗?请写出来,并说明理由。
(2)如果CD= 3,BC= 5,你能求出哪些线段的长?
A
D
B
C
∟
∟
2.如图已知∠1=∠2,若再增加一个条
件能使结论AB·ED=AD·BC成立,则这
个条件可以是_________________。
2
1
A
C
E
B
D
分析:①从角的角度思考:∠D=∠B或∠AED=∠C
② 从边的角度思考:AD:AB=AE:AC
如图:在Rt△ABC中,有正方形DEFG,且E、F在斜边BC上,D、G分别在AB、AC上.试说明:EF2=BE·FC
G
F
E
D
C
B
A
解:
四边形DEFG是正方形
∠DEB=∠GFC=90°,
EF=DE=FG.
∵
∴
又∵ ∠B+∠C=90°,∠B+∠BDE=90°
∴
∠BDE=∠C
Rt△BED∽ Rt△GFC
∴
BE
DE
FC
GF
=
∴
BE
EF
FC
EF
=
∴
∴
EF2=BE·FC
F
E
D
C
B
A
如图:已知∠BAC=90°,BD=DC, DE⊥BC交AC于E,交BA的延长线于F.试说明:AD2=DE·DF
由AD2=DE·DF,得
故只要说明△ADE∽ △FDA即可
分析:
AD
DE
AD
DF
=
点评:证明乘积式时,可先将乘积式改为比例式,然后找相似三角形(或平行线)
1.相似三角形对应高的比等于相似比。
2.相似三角形对应中线的比等于相似比。
3.相似三角形对应角平分线的比等于相似比。
相似三角形的性质:
4.相似三角形周长的比等于相似比。
5.相似三角形面积的比等于相似比的平方。
