八年级数学上册第十二章_12[1][1].2作轴对称图形课件
文档属性
| 名称 | 八年级数学上册第十二章_12[1][1].2作轴对称图形课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-07 15:06:25 | ||
图片预览






文档简介
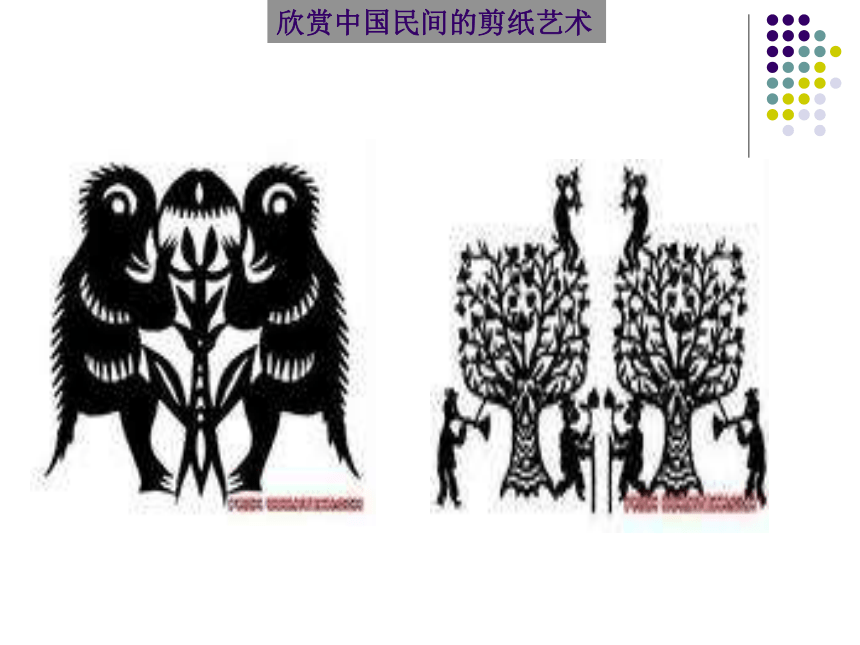
课件22张PPT。12.2.1作轴对称图形 欣赏中国民间的剪纸艺术欣赏中国民间的剪纸艺术欣赏中国民间的剪纸艺术学习目标:
1.会作已知图形关于某条直线对称的图形。
2.能利用轴对称的一些性质设计图案。一、回顾旧知识 1、如果一个图形沿一条直线折叠,直线两旁的
部分能够互相重合,这个图形就叫做轴对称图形。 2、如果两个图形关于某条直线对称,那么对
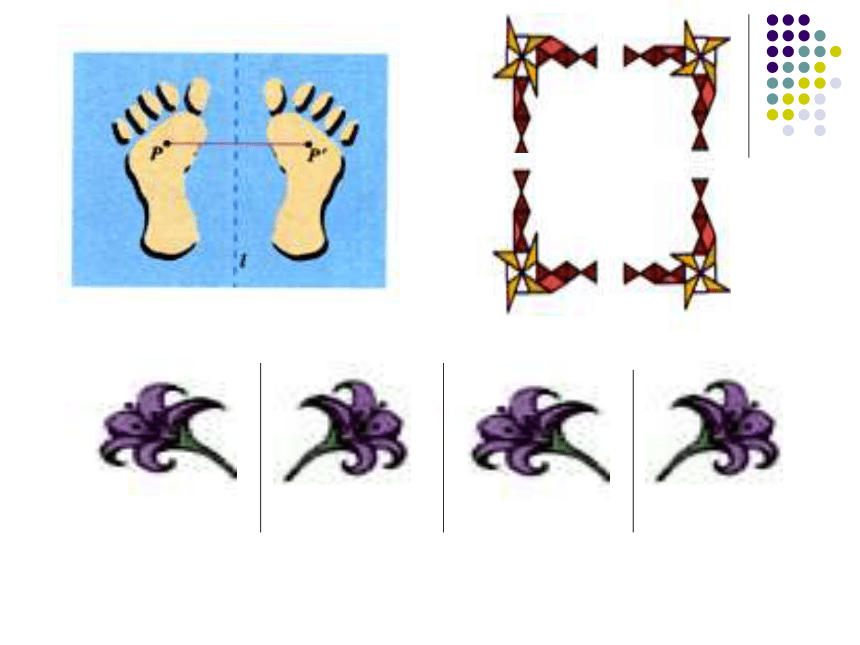
称轴是任何一对对应点所连线段的垂直平分线。预习导学在一 张半透明的纸的左边画一只左手印,再把这张纸对折后描图,打开对折的纸。就能得到相应的右手印。动脑想一 想左手印和右手印有什么关系?成轴对称。对称轴是折痕所在的直线,即直线图中的 与 m 是什么关系?m。m..p二、预习检测轴对称变换由一个平面图形得到它的轴对称图形叫做轴对称变换 对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化。来吧!动动脑筋动动手三、探究性质: 1、由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全一样。 2、新图形上的每一点,都是原图形上的某一点关于直线L的对称点。 3、连接任意一对对应点的线段被对称轴垂直平分。┓┓┓合作探究: 如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?∴ 点A′即为所求M l ┓O 基础一 l l 已知直线L和线段AB,作出线段AB与A′B′关于直线 L对称的图形。MN┓┓OP基础二∴线段A′B′即为所求例1如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。┐┐┐l作法:(1)过点A作直线l的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点。(4)连接A′B′、B′C′、C′A′,得到△A′B′C′即为所求。OPM(2)过点B作直线l的垂线,垂足为点P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点。(3)过点C作直线l的垂线,垂足为点M,在垂线上截取MC′=MC,点C′就是点C关于直线l的对称点。归纳1、找特征点2、作垂线3、截取等长4、依次连线作图步骤归纳总结 几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形。 对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对称点,就可以得到原图形的轴对称图形。
当堂达标 :
1、如图,把下列图形补成关于直线L的对称图形。 2. 请画出⊿ABC关于直线 的对称⊿ A’B’C’.(1)轴对称变换的定义 ? 今天你学到了什么 ? 回顾小结 (2) 利用轴对称性质作图作业布置 课本45-46页:习题第1题、第5题。
再见
1.会作已知图形关于某条直线对称的图形。
2.能利用轴对称的一些性质设计图案。一、回顾旧知识 1、如果一个图形沿一条直线折叠,直线两旁的
部分能够互相重合,这个图形就叫做轴对称图形。 2、如果两个图形关于某条直线对称,那么对
称轴是任何一对对应点所连线段的垂直平分线。预习导学在一 张半透明的纸的左边画一只左手印,再把这张纸对折后描图,打开对折的纸。就能得到相应的右手印。动脑想一 想左手印和右手印有什么关系?成轴对称。对称轴是折痕所在的直线,即直线图中的 与 m 是什么关系?m。m..p二、预习检测轴对称变换由一个平面图形得到它的轴对称图形叫做轴对称变换 对称轴方向和位置发生变化时,得到的图形的方向和位置也会发生变化。来吧!动动脑筋动动手三、探究性质: 1、由一个平面图形可以得到它关于一条直线L成轴对称的图形,这个图形与原图形的形状、大小完全一样。 2、新图形上的每一点,都是原图形上的某一点关于直线L的对称点。 3、连接任意一对对应点的线段被对称轴垂直平分。┓┓┓合作探究: 如果有一个图形和一条直线,如何作出与这个图形关于这条直线对称的图形呢?∴ 点A′即为所求M l ┓O 基础一 l l 已知直线L和线段AB,作出线段AB与A′B′关于直线 L对称的图形。MN┓┓OP基础二∴线段A′B′即为所求例1如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形。┐┐┐l作法:(1)过点A作直线l的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点。(4)连接A′B′、B′C′、C′A′,得到△A′B′C′即为所求。OPM(2)过点B作直线l的垂线,垂足为点P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点。(3)过点C作直线l的垂线,垂足为点M,在垂线上截取MC′=MC,点C′就是点C关于直线l的对称点。归纳1、找特征点2、作垂线3、截取等长4、依次连线作图步骤归纳总结 几何图形都可以看作由点组成,只要作出这些点关于对称轴的对应点,再连接对应点,就可以得到原图形的轴对称图形。 对于一些由直线、线段或射线组成的图形只要作出图形中的一些特殊点的对称点,再连接对称点,就可以得到原图形的轴对称图形。
当堂达标 :
1、如图,把下列图形补成关于直线L的对称图形。 2. 请画出⊿ABC关于直线 的对称⊿ A’B’C’.(1)轴对称变换的定义 ? 今天你学到了什么 ? 回顾小结 (2) 利用轴对称性质作图作业布置 课本45-46页:习题第1题、第5题。
再见
